Show that the area of the triangle contained between the vectors a and b is one half of the magnitude of a×b.Solution in Punjabi
Step by step video & image solution for Show that the area of the triangle contained between the vectors a and b is one half of the magnitude of a xx b. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Some of the most profound statements on the nature of science have come from Albert Einstein, one of the greatest scientists of all time. What do you think did Einstein mean when he said : "The most incomprehensible thing about the world is that it is comprehensible"?
View SolutionA geyser heats water flowing at the rate of 3.0 litres per minute from 27∘C to 77∘C. If the geyser operates on a gas burner, what is the rate of consumption of the fuel if its heat of combustion is 4.0×104J/g ?
View SolutionShow that the area of the triangle contained between the vector overset rarr(r ) and overset rarr(b) is one half of the magnitude of overset rarr(a) xx overset rarr(b)
View Solutionदर्शाइए कि →aएवं→b के बीच बने त्रिभुज का क्षेत्रफल →a×→b के परिमाण का आधा है।
View SolutionThe resultant of two vectors A and B is perpendicular to vector A and its magnitude is equal to half of the magnitude of vector B. Then the angle between A and B is
View SolutionThe resultant of two vectors A and B is perpendicular to the vector A and its magnitude is equal to half the magnitude of vector B. The angle between A and B is -
View SolutionShow that the area of the triangle contained between the →aand→b is is one half of the magnitude of →a×→b.
View SolutionThe resultant of two vectors A and B is perpendicular to vector A and its magnitude is equal to half of the magnitude of vector B . Then the angle between A and B is :
(a) 30∘ (b) 45∘
(c) 150∘ (d) 120∘
View SolutionShow that the area of the triangle contained between the vectors a and b is one half of the magnitude of a×b.
View SolutionShow that the area of the triangle contained between the vectors a and b is one half of the magnitude of a × b .
View SolutionShow that the area of the triangle contained between the vector overset rarr(a ) and overset rarr(b) is one half of the magnitude of overset rarr(a) xx overset rarr(b)
View SolutionShow that the area of the triangle contained between the vectors J and $ is one haif0fthe magnitude of →a×→b.
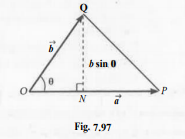
View SolutionShow that the area of the triangle contained between the vectors veca and vecb is one half of the magnitude of vecaxxvecb .
View SolutionIf two vectors are represented by the two sides of a triangle , then show that half the magnitude of their cross product will give the area of the triangle .
View SolutionShow that the area of the triangle contained between the vectors →Aand→B is one-half the magnitude of →A×→B.
View Solution
