A projectile launched from the ground landed a horizontal distance of 120.0m from its launch point. The projectile was in the air for a time of 4.00 seconds. If the projectile landed at the same vertical position from which it was launched what was the launch speed of the projectile? Ignore air resistance. A 22.4 m/s B 30.0 m/s C 36.1 m/s D 42.4 m/s E 50.0 m/s
Correct option C 36.1 m/sTo travel 120m horizontally in 4s gives vx = 30 m/s. The time to reach maximum height was 2 seconds and vy = 0 at the maximum height which gives viy = 20m/s. vi = √vx2 + viy2
Related Solutions
A projectile is launched from the ground and it returns to the ground level. The horizontal range of the projectile is R= 175 m . If the horizontal component of the projectile's velocity at any instant is , then determine the time of flight of the projectile.
View Solutionwith horizontal 60^@ A projectile is launched from the ground making an angle of with the projectile horizontal after 1 s 30^@ makes an angle. The maximum height attained by the projectile is : ( g = 10 m s^(-2) take)
View Solution40 m ऊँची पहाड़ी से एक प्रक्षेप्य 50 m/s की प्रारंभिक चाल से प्रक्षेपित किया गया । जमीन पर टकराते समय इसकी चाल ज्ञात करें ।
View SolutionThe position of a projectile launched from the origin at t = 0 is given by s = (40hati+50hatj)m at t=2s . if the projectile was launched at an angle theta from the horizontal, then theta is (take g = 10 ms^(–2)
View SolutionThe highest barrier that a projectile can clear is 13.5 m, when the projectile is launched at an angle of above the horizontal. What is the projectile's launch speed?
View SolutionFrom the ground, a projectile is fired at an angle of 60 degree to the horizontal with a speed of The horizontal range of the projectile is
View SolutionFrom the ground, a projectile is fired at an angle of 60 degree to the horizontal with a speed of 20" m s"^(-1) The horizontal range of the projectile is
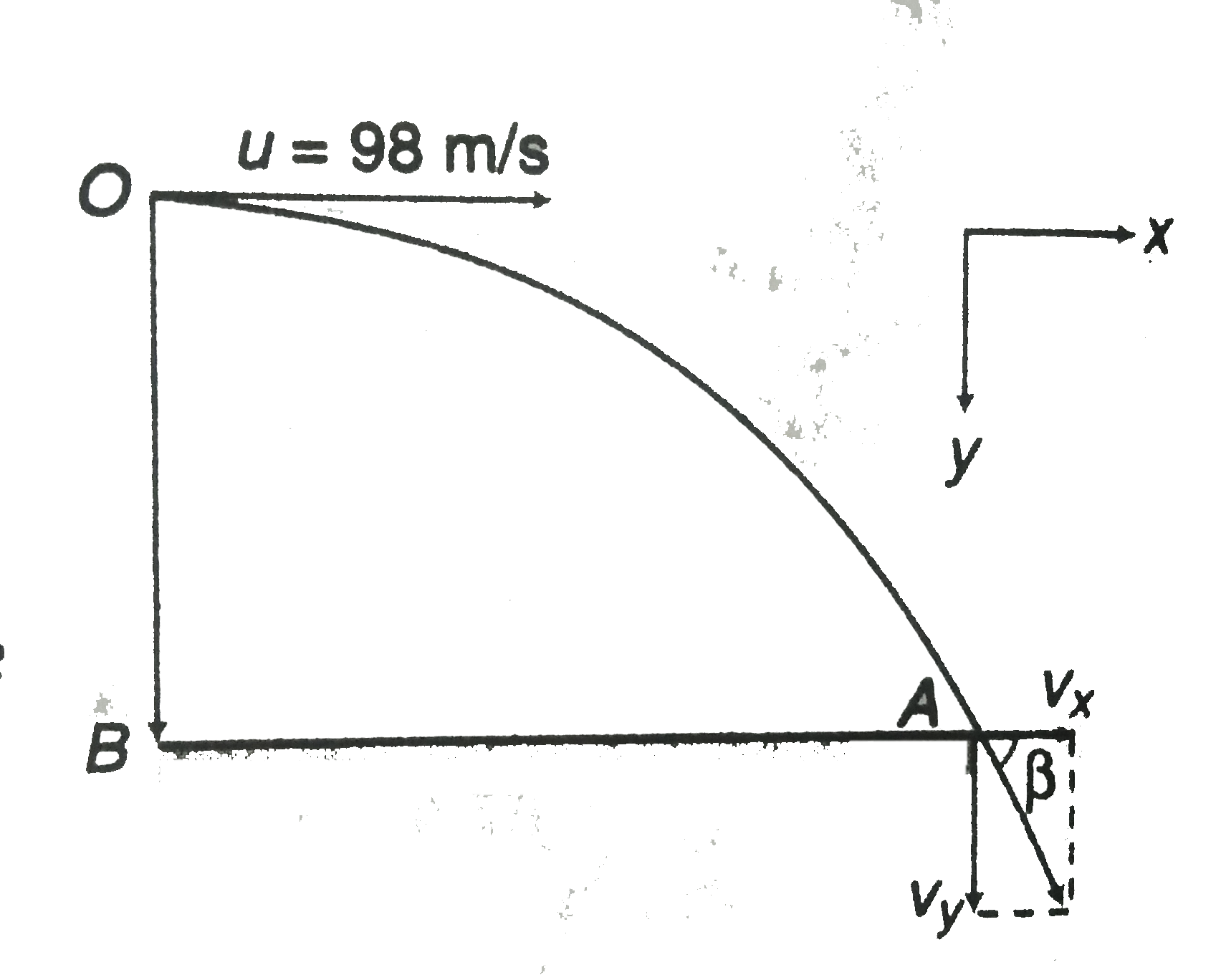
View SolutionA projectile is fired horizontally with velocity of 98 m/s from the top of a hill 490 m high. Find (a) the time taken by the projectile to reach the ground, (b) the distance of the point where the particle hits the ground from foot of the hill and (c) the velocity with which the projectile hits the ground. (g= 9.8 m//s^2) .
View SolutionA projectile is fired horizontally with velocity of 98 m/s from the top of a hill 490 m high. Find
(a) the time taken by the projectile to reach the ground,
(b) the distance of the point where the particle hits the ground from foot of the hill and
(c) the velocity with which the projectile hits the ground.
 .
.
View SolutionThe position of a projectile launched from the origin at t = 0 is given by vecr =(40hati+50hatj)m at t=2s. If the projectile was launched at an angle theta from the horizontal, then theta is (take g = 10 ms^(-2) )
View SolutionA projectile fired from a gun has initial horizontal and vertical components of velocity equal to 30 m/s and 40 m/s, respectively.
What is the speed of the projectile when it is at the highest point in its trajectory?
View Solutionएक प्रक्षेप्य को प्रारम्भिक वेग से प्रक्षेपित करते हैं। यदि प्रक्षेप्य की क्षैतिज परास इसके द्वारा प्राप्त की गयी अधिकतम ऊँचाई की दुगनी है, तो :
View Solutionएक प्रक्षेप्य को क्षैतिज तल में एक बिन्दु से इस प्रकार प्रक्षेपित करते हैं कि इसके वेग के क्षैतिज व ऊर्ध्वाधर घटक क्रमशः 9.8 m/s तथा 19.6 m/s है तो क्षैतिज परास ज्ञात कीजिए।
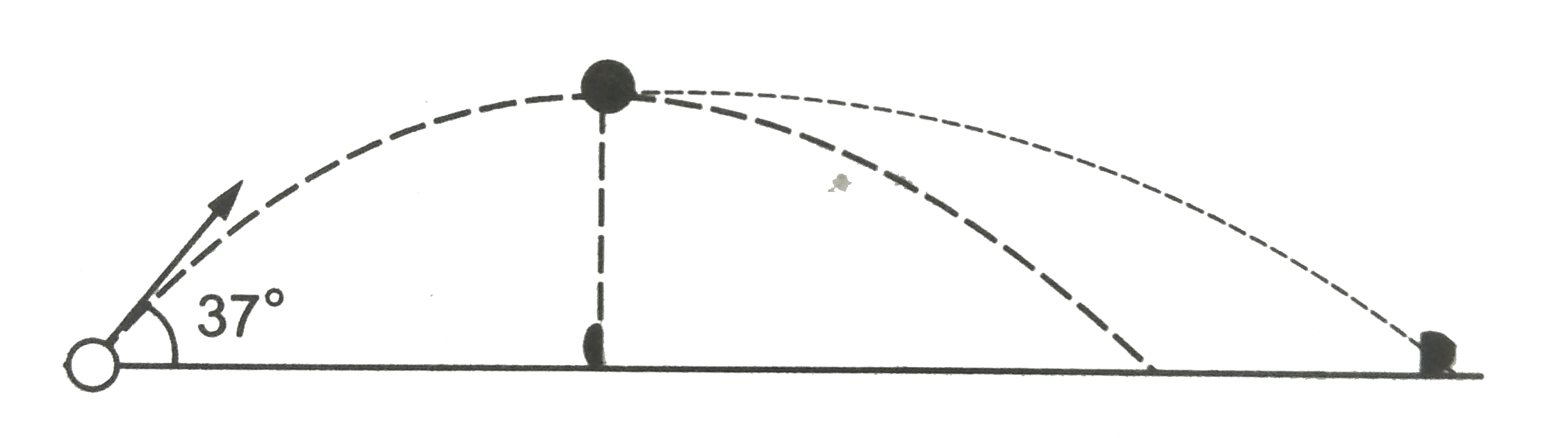
View SolutionA projectile is fired at a speed of 100 m/s at an angle of 37^(@) above the horizontal. At the highest point, the projectile breaks into two parts of mass ratio 1 : 3, the smaller piece coming to rest. Find the distance from the launching point to the point where the heavier piece lands.
View SolutionA projectile is fired at a speed of 100 m/s at an angle of 37^(@) above the horizontal. At the highest point, the projectile breaks into two parts of mass ratio 1:3, the smaller piece coming to rest. Find the distance from the launching point to the point where the heavier piece lands.
View SolutionA projectile is fired at a speed of 100 m/s at an angle of 37° above the horizontal. At the highest point, the projectile breaks into two parts of mass ratio 1 :3, the smaller coming to rest. Find the distance from the launching point to the point where the heavier piece lands.
View SolutionVelocity of a projectile at height from ground is . Here is in horizontal direction and is vertically upwards. Then
Speed with which particle is projected from ground is……… m/s
View SolutionVelocity of a projectile at height 15 m from ground is v=(20hati+10hatj)m//s . Here hati is in horizontal direction and hatj is vertically upwards. Then Speed with which particle is projected from ground is……… m/s
View SolutionTwo seconds after being projected from ground level, a projectile is displaced 40 m horizontally and 58 m vertically above its launch point. What are the (a) horizontal and (b) vertical components of the initial velocity of the projectile? (c ) At the instant the projectile achieves its maximum height above ground level, how far is it displaced horizontally from the launch point?
View SolutionA projectile is fired at a speed of 100 m/s at an angel of above the horizontal. At the highest point, the projectile breaks into two parts of mass ratio 1:3 the smaller coming to rest. Find the distance from the launching point to the where the heavier piece lands.
View Solution