A resistor and an inductor in series are connected to a battery through a switch. After the switch is closed at t = 0 A joule heat dissipation in the resistor changes at fastest rate at t = L/Rln2B when the rate of increase of magnetic energy stored in the coil is at maximum current in the circuit is V/2RC power dissipated in resistor increases continuously but rate of change of power initially increases it later reaches a maximum and beyond a point decreases to zero D the fastest increase of current takes place at I = V/2R
Correct option: a b cExplanation:
Related Solutions
A resistor and inductor are connected in series through a battery. The switch is closed at time t=0 . Then what is the magnitude of current flowing when rate of increases of magnetic energy in the inductor is maximum
View SolutionA 50 mH inductor is in series with a 10 ohm resistor and a battery with an emf of 25 V. At t = 0 the switch is closed. Find the power dissipated in the resistor
View SolutionAn ideal inductor, (having initial current zero) a resistor and an ideal battery are connected in series at time t = 0 . At any time t , the battery supplies energy at the rate P_(B) , the resistor dissipates energy at the rate P_(R ) and the inductor stores enegy at the rate P_(L) .
View SolutionThe switch shown in figure is suddenly closed. Find the current through the resistor when energy dissipated in the resistor is one third of total energy dissipated in the resistor.

View SolutionThe switch shown in figure is suddenly closed. Find the current through the resistor when energy dissipated in the resistor is one third of total energy dissipated in the resistor.
View SolutionAn unknown resistor is connected between the terminals of a 3.00 V battery. Energy is dissipated in the resistor at the rate of 0.707 W. The same resistor is then connected between the terminals of a 12.0 V battery. At what rate is energy now dissipated?
View SolutionIf the current through a resistor in a circuit increases by 3%, the power dissipated by the resistor
View SolutionJoule Heating Law#!#Power Dissipated by a Resistors#!#Power Rating
View Solution5 A 50 mH inductor is in series with a 10 2 resistor and a battery with an emf oj 25 V. At t = 0 the switch is closed. Find Q(d) the power dissipated in the resistor
View Solutionan inductor of inductance 2.00 H is joined in series with a resistor of resistance and a battery of emf 2.00 V. At t = 10 ms, find (a) th current in the circuit, (b) the power delivered by the batter, (c ) the power dissipated in heating the resistor and (d) the rate at which energy is being stored in magnetic field.
View Solutionan inductor of inductance 2.00 H is joined in series with a resistor of resistance and a battery of emf 2.00 V. At t = 10 ms, find (a) th current in the circuit, (b) the power delivered by the batter, (c ) the power dissipated in heating the resistor and (d) the rate at which energy is being stored in magnetic field.
View SolutionAn inductor of 5 m H is connected in series with a resistor of resistance 4 . A battery of 2 V is connected across the circuit through a switch . Calculate the rate of growth of current just after the switch is on .
View SolutionResistor of resistance R and a capacitor of capacitance Care connected in series to a battery of emf E, through a switch and this circuit is called A. Similarly, inductor of inductance L and resistor of resistance R are connected in series to a battery of emf Ethrough a switch and this circuit is called B. Switches in both the circuits A and B are closed at t= 0.
View Solution5A 50 mH inductor is in series with a 10 2 resistor and a battery with an emf oj 25 V. At t = 0 the switch is closed. Find Q(c) the rate at which energy is stored in the inductor,
View SolutionConsider a circuit consists of resistors, inductor, battery and a switch as shown. Resistance of resistors, inductance of inductor and of battery are indicated. The switch is closed at .

Find current through at steady state
View SolutionConsider the circuit in Fig. When the switch is closed in position and opens in position , electrical work must be performed on the inductor and on the resistor. The energy stored in the inductor is for the resistor energy appears as heat.
a. What is the ratio of of the rate at which energy is stored in the inductor to the rate at which energy is dissipated in the resistor?
b. Express the ratio as a function of time.
c. If the time constant of circuit is , what is the time at which ?
View SolutionConsider the circuit in Fig. When the switch is closed in position and opens in position , electrical work must be performed on the inductor and on the resistor. The energy stored in the inductor is for the resistor energy appears as heat.
a. What is the ratio of of the rate at which energy is stored in the inductor to the rate at which energy is dissipated in the resistor?
b. Express the ratio as a function of time.
c. If the time constant of circuit is , what is the time at which ?
View SolutionConsider a circuit consists of resistors, inductor, battery and a switch as shown. Resistance of resistors, inductance of inductor and of battery are indicated. The switch is closed at .
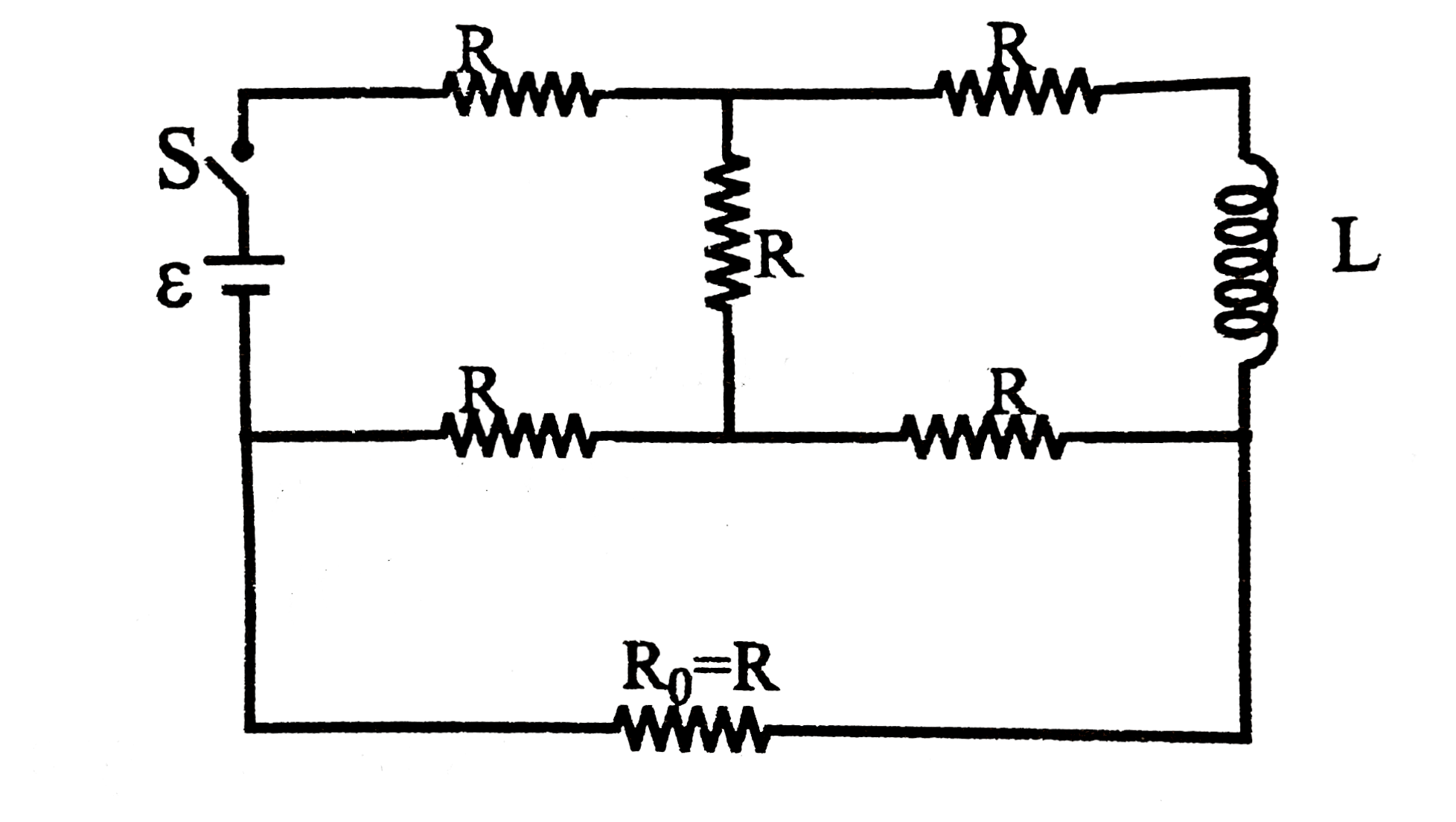
Find time constant of LR circuit during growth of current
View SolutionConsider a circuit consists of resistors, inductor, battery and a switch as shown. Resistance of resistors, inductance of inductor and EMF of battery are indicated. The switch is closed at t=0 . After a long time switch is opened. Find heat generated through the resistor R_(0)
View SolutionIn the circuit shown in figure, the current through each resistor is I. Find the currents through the resistors immediately after the switch ‘S’ is opened. How much heat will get dissipated in the circuit after thw switch is opened ?
View Solution