An inductor of 5 m H is connected in series with a resistor of resistance 4 Ω . A battery of 2 V is connected across the circuit through a switch . Calculate the rate of growth of current just after the switch is on .
The correct Answer is:400As−1
To solve the problem of finding the rate of growth of current just after the switch is closed in a circuit with an inductor and a resistor, we can follow these steps:
1. Identify the Circuit Parameters:
- Inductance (L) = 5 mH = 5×10−3 H
- Resistance (R) = 4 Ω
- Voltage (V) = 2 V
2. Apply Kirchhoff's Voltage Law:
When the switch is closed, we can apply Kirchhoff's law to the circuit. The voltage provided by the battery (V) is equal to the sum of the voltage drops across the resistor (IR) and the inductor (L dIdt):
V=IR+LdIdt
3. Rearranging the Equation:
Rearranging the equation gives us:
LdIdt=V−IR
4. Finding the Rate of Change of Current:
We want to find dIdt just after the switch is closed (at t=0). At this moment, the current (I) is 0 because the inductor initially opposes any change in current. Therefore, substituting I=0 into the equation:
LdIdt=V−0⋅R
This simplifies to:
LdIdt=V
5. Solving for dIdt:
Now, we can solve for dIdt:
dIdt=VL
6. Substituting the Values:
Substitute the values of V and L:
dIdt=2V5×10−3H=20.005=400A/s
Final Answer:
The rate of growth of current just after the switch is closed is 400A/s.
---
- Inductance (L) = 5 mH = 5×10−3 H
- Resistance (R) = 4 Ω
- Voltage (V) = 2 V
When the switch is closed, we can apply Kirchhoff's law to the circuit. The voltage provided by the battery (V) is equal to the sum of the voltage drops across the resistor (IR) and the inductor (L dIdt):
V=IR+LdIdt
Rearranging the equation gives us:
LdIdt=V−IR
We want to find dIdt just after the switch is closed (at t=0). At this moment, the current (I) is 0 because the inductor initially opposes any change in current. Therefore, substituting I=0 into the equation:
LdIdt=V−0⋅R
This simplifies to:
LdIdt=V
Now, we can solve for dIdt:
dIdt=VL
Substitute the values of V and L:
dIdt=2V5×10−3H=20.005=400A/s
The rate of growth of current just after the switch is closed is 400A/s.
Topper's Solved these Questions
- ALTERNATING CURRENT Book:MODERN PUBLICATIONChapter:ALTERNATING CURRENT Exercise:CONCEPTUAL QUESTIONS
Explore 25 Videos
- ALTERNATING CURRENT Book:MODERN PUBLICATIONChapter:ALTERNATING CURRENT Exercise:TOUGH & TRICKY PROBLEMS
Explore 12 Videos
- ALTERNATING CURRENT Book:MODERN PUBLICATIONChapter:ALTERNATING CURRENT Exercise:CHAPTER PRACTICE TEST
Explore 16 Videos
- ATOMS Book:MODERN PUBLICATIONChapter:ATOMS Exercise:Chapter Practice Test
Explore 16 Videos
Similar Questions
How much current will flow through a resistor of resistor of resistance 12Ω if a battery of 18 V is connected across it ?
View SolutionA cell of 1.5V is connected across an inductor of 2mH in series with a 2Ω resistor. What is the rate of growth of current immediately after the cell is switched on.
View Solution
Knowledge Check
A coil of inductance 0.20H is connected in series with a switch and a cell of emf 1.6V. The total resistance of the circuit is 4.0Ω. What is the initial rate of growth of the current when the switch is closed?
A0.050As−1B0.40As−1C0.13As−1D8.0As−1An ideal coil of 10H is connected in series with a resistance of 5(Ω) and a battery of 5V. 2second after the connections is made, the current flowing in ampere in the circuit is
A(1−e−1)B(1−e)CeDe−1An inductor of 20 H and a resistance of 10Ω, are connected to battery of 5 volt in series, then initial rate of change of current is :-
A0.5amp/sB2.0amp/sC2.5amp/sD0.25amp/s
in the figure shown , a circuit contains two identical resistors with resistance R=Ω and an inductance with L=2 H ,An ideal battery of 15 V is connected in the circuit what will be the current through the battery long after the switch is clossed ?
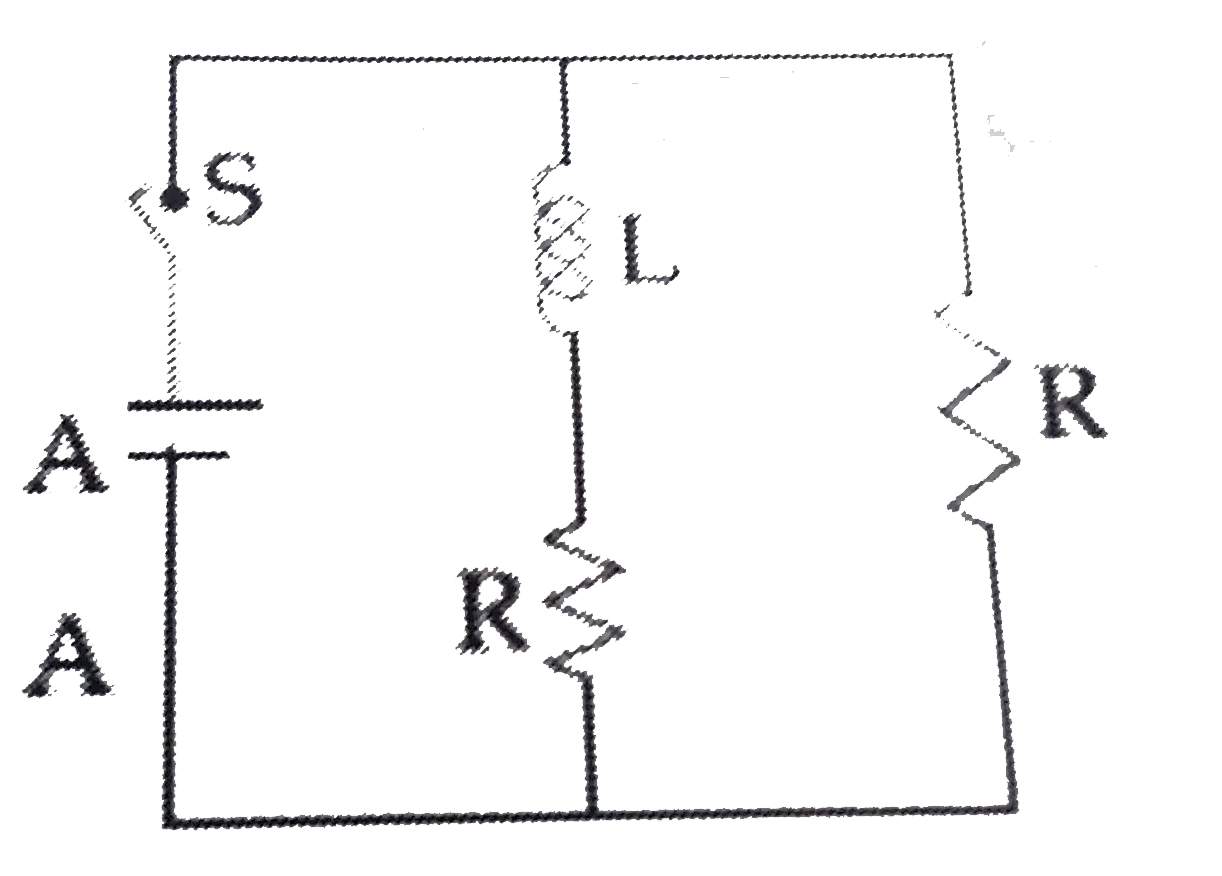
View SolutionA 6-V battery is connected across a 5−Ω resistor.Calculate the current passing through the resistor .
View SolutionAn inductor of inductance 5.0 H, having a negligible resistance, is connected in series with a 100Ω resistor and a battery of emf 2.0 V. Find the potential difference across the resistor 20 ms after the circuit is switched on.
View SolutionAn inductor of 10 mH is connected to a 20 V battery through a resistor of 10 kΩ and a switch. After a long time, when maximum current is set up in the circuit, the current is switched off. The current in the circuit after μs is x100 mA Then x is equal to ____________. (Take e−1=0.37)
View SolutionTwo cells E1 and E2 of emfs 4 V and 8 V having internal resistances 0.5Ω and 1.0Ω respectively are connected in opposition to each other. This combination is connected in series with resistances of 4.5Ω and 3.0Ω. Another resistance is connected in parallel across the 3Ω resistor.
(a) Draw the circuit diagram
(b) Calculate the total current flowing through the circuit.
View Solution

