An infinite dielectric sheet having charge density σ has a hole of radius R in it. An electron is released on the axis of the hole at a distance √3R from the centre. The speed with which crosses the centre of the hole.d None of these
Correct option: b Explanation: Since the potential function is not defined for an infinite conducting sheet hence to solve this problem we either calculate potential difference or use force equations Electric field due to an infinite dielectric sheetElectric field at the axis of a disc of radius R is
Related Solutions
An infinite dielectric sheet having charge density has a hole of radius in it. An electron is released on the axis of the hole at a distance from the center. Find the speed with which it crosses the center of the hole.

View SolutionAn infinite dielectric sheet having charge density has a hole of radius in it. An electron is released on the axis of the hole at a distance from the center. Find the speed with which it crosses the center of the hole.

View SolutionAn infinite dielectric sheet having charge density has a hole of radius R in it. An electron is released from point P on the axis of the hole at a distance from the center. Find the speed with which it crosses the plane of the sheet.
 .
.
View SolutionAn infinite dielectric sheet having charge density sigma has a holeof radius R in it. An electrom is released from point P on the axis of the hole at a distance sqrt(3)R from the center. Find the speed with which it crosses the plane of the sheet. .
View SolutionAn infinite dielectric sheet having charge density sigma has a holeof radius R in it. An electrom is released from point P on the axis of the hole at a distance sqrt(3)R from the center. Find the speed with which it crosses the plane of the sheet. .
View SolutionA uniform disc of radius R has a hole cut out which has a radius r. The centre of hole is at a distance (R )/(2) from the centre of disc. The position of centre of mass is :
View SolutionCalculate electric field at a point on axis, which at a distance x from centre of uniformly charged disc having surface charge density sigma and R which also contains a concentric hole of radius r.
View SolutionIn the figure shown, find out centre of mass of a system of a uniform circular plate of radius 3R from O in which a hole of radius R is cut whose centre is at 2R distance from the centre of large circular plate
View SolutionIn the figure shown, find out centre of mass of a system of a uniform circular plate of radius 3R from O in which a hole of radius R is cut whose centre is at 2R distance from the centre of large circular plate
View SolutionFind the position of centre of mass of a uniform disc of radius R from which a hole of radius is cut out. The centre of the hole is at a distance R/2 from the centre of the disc.
View SolutionA disc (of radius r cm) of uniform thickness and uniform density has a square hole with sides of length . One corner of the hole is located at the centre of the disc and centre of the hole lies y-axis as shown. Then the y-coordinate of position of centre of mass of disc with hole (in cm) is.
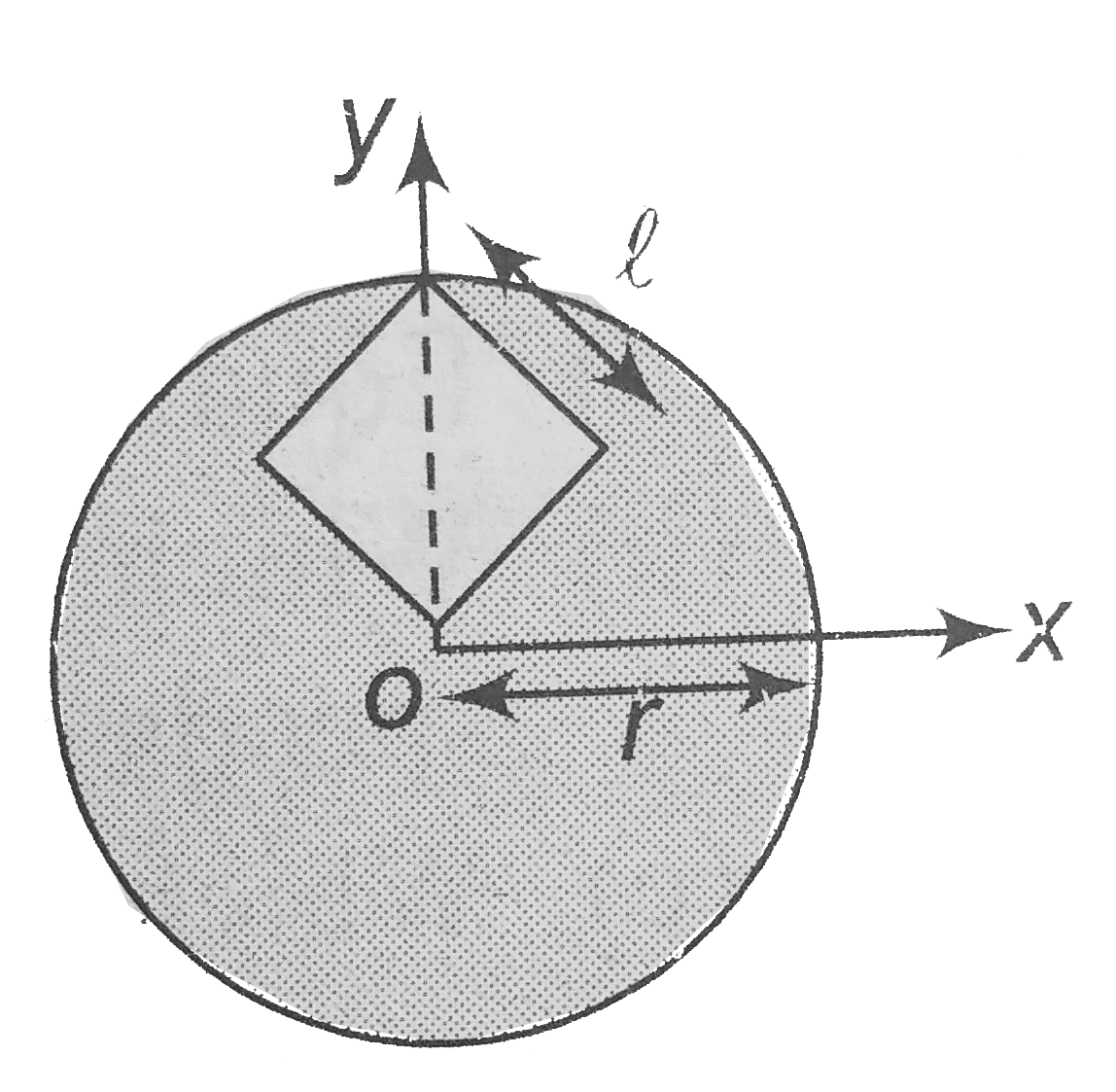 .
.
View SolutionA disc (of radius r cm) of uniform thickness and uniform density sigma has a square hole with sides of length l = (r )/(sqrt(2)) cm . One corner of the hole is located at the centre of the disc and centre of the hole lies y-axis as shown. Then the y-coordinate of position of centre of mass of disc with hole (in cm) is. .
View Solutionदो अनन्त विस्तार की आवेशित धातु की प्लेटों A और B बराबर परन्तु विपरीत पृष्ठ आवेश घनत्व है। प्लेटों के मध्य दूरी d है। प्लेट B में एक छोटा छिद्र है इस छिद्र के सामने प्लेट A से एक इलेक्ट्रॉन (स्थिर अवस्था से ) छोडा जाता है। इलेक्टॉन किस वेग से छिद्र से बाहर निकलेगा A पर ऋण आवेश हें
View SolutionA hole of radius r is cut from a uniform disc of radius 2r. Centre of the hole is at a distance r from centre of the disc. Locate centre of mass of the remaining part of the disc.
View SolutionAn electron released on the axis of a positively charged ring at a large distance from the centre will
View SolutionA circular hole is cut from a disc of radius 6 cm in such a way that the radius of the hole is 1 cm and the centre of 3 cm from the centre of the disc. The distance of the centre of mass of the remaining part from the centre of the original disc is
View SolutionA circular hole is cut from a disc of radius 6 cm in such a way that the radius of the hole is 1 cm and the centre of 3 cm from the centre of the disc. The distance of the centre of mass of the remaining part from the centre of the original disc is
View SolutionFrom a uniform disk of radius R, a circular hole of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of gravity of the resulting flat body.
View SolutionFrom a uniform disk of radius R, a circular hole of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of gravity of the resulting flat body.
View SolutionFrom a uniform disk of radius R, a circular hole of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of gravity of the resulting flat body.
View Solution