Let ABCDEF be a convex hexagon in which the diagonals AD BE CF are concurrent at O. Suppose the area of triangle OAF is the geometric mean of those of OAB and OEF and the area of triangle OBC is the geometric mean of those of OAB and OCD. Prove that the area of triangle OED is the geometric mean of those of OCD and OEF.
Explanation:Let OA = a OB = b OC = c OD = d OE = e OF = f [OBA] = x [OCD] = y [OEF] = z [ODE] = u [OFA] = v [OBC] = w. We are given that v 2 = zx w2 = xy and we have to prove that u2 = yz. Since ∠AOB = ∠DOE we have
Related Solutions
O The point at the interior of a square ABCD is such that OAB is an equilateral triangle. Prove that Delta OCD Is an isosceles triangle.
View Solutionचित्र में, ABCDEF एक षटभुज है जिसका केन्द्र O है | यदि त्रिभुज OAB का क्षेत्रफल 9 वर्ग सेमी. हो, तो
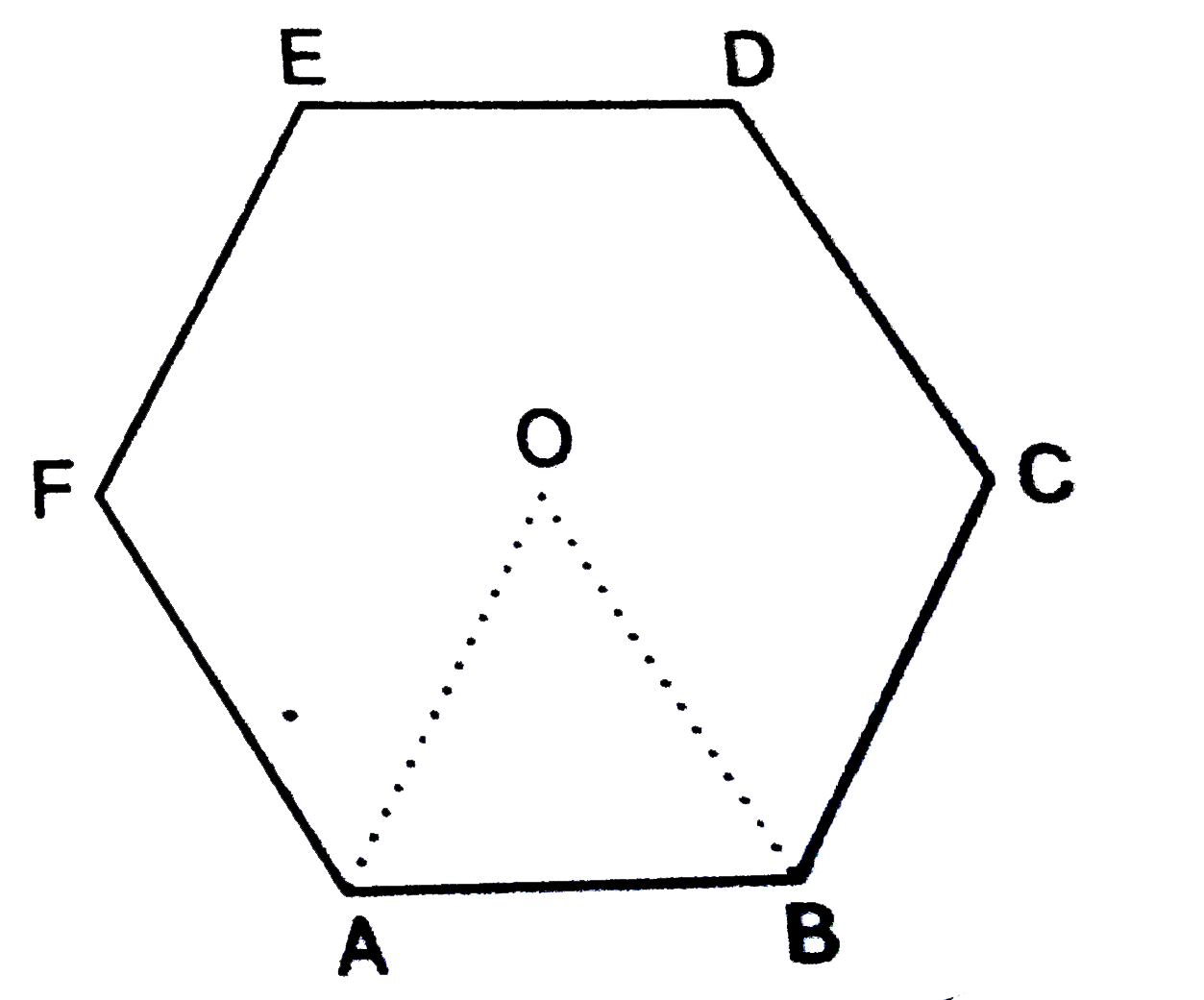
षटभुज तथा
View SolutionO is a point in the interior of a square ABCD such that is an equilateral triangle . Show that is an isoceles triangle .
View Solutionis a point in the interior of a square such that is an equilateral triangle . Show that is an isosceles triangle .
View Solutionचित्र में, ABCDEF एक षटभुज है जिसका केन्द्र O है | यदि त्रिभुज OAB का क्षेत्रफल 9 वर्ग सेमी. हो, तो

एक वृत्त जिसके अन्दर षटभुज बना हो, का क्षेत्रफल ज्ञात कीजिए |
View SolutionLet O be a point inside such that
Area of is equal to
View SolutionIn a quadrilateral AB|\|CD the diagonals intersect at ‘O’. Then S.T. /_\OAB ~ /_\OCD .
View SolutionProve that the product geometric means between two quantities is equal to the nth power of geometric mean of those two quantities.
View SolutionProve that the product geometric means between two quantities is equal to the nth power of geometric mean of those two quantities.
View Solutionसमलम्ब चतुर्भुज ABCD में भुजाएँ AB तथा DC समान्तर हैं और AB = 2DC और उसके विकर्ण बिन्दु0 पर मिलते हैं, तो त्रिभुज OAB तथा OCD के क्षेत्रफलों का अनुपात है।
View Solutionयदि तथा तब का क्षेत्रफल (वर्ग इकाई में) ज्ञात कीजिए।
View SolutionThe graph of forms a triangle OAB with the coordinate axes, where O is the origin . Also the graph of forms a tringle OCD with the coordinate axes. Then the area of is equal to
View SolutionThe point H orthocentre of the triangle ABC. A point K is taken on the straight line CH such that ABK is a right triangle. Prove that the area of the triangle ABK is the geometric mean between the area of the triangles ABC and ABH.
View SolutionIn , the medians AD, BE and CF meet at O. What is the ratio of the area of to the area of ?
View SolutionIn , the medians AD. BE and CF meet at O. What is the ratio of the area of to the area of ?
View SolutionIn the isosceles triangle OAB, O is the origin, . If the equation of side AB is , then the area of the triangle OAB is (in square units)
View Solutiono is the origin. A and B are variable points on y =x and x +y=0 such that the area of triangle OAB is k^2. The locus of the circumcentre of triangle OAB is
View SolutionIn the given figure, G, a point on the circle, is the centroid of the triangle OAB. Find the ratio of the area of the equilateral triangle OAB to that of the circle whose centre is O.
View SolutionFrom the given map Delta OAB Area
View Solutionयदि दो संख्याओं के समांतर माध्य एवं गुणोत्तर माध्य में का अनुपात हो, तो सिद्ध करो की उन संख्याओं में का अनुपात है।
View Solution