In triangle ABC let D be the midpoints of BC if ∠ADB = 45° and ∠ACD = 30° determine ∠BAD.
Explanation:Draw BL Perpendicular to AC and join L to D . See Fig 2.Since ∠BCL = 30° we get ∠CBL = 60°. Since BLC is right-triangle with ∠BCL = 30° we have BL = BC/2 = BD . Thus in triangle BLD we observed that BL = BD and ∠DBL = 60°. This implies that BLD is an equilateral triangle and hence LB = LD . Using ∠ LDB = 60° and ∠ADB = 45° we get ∠ ADL = 15° . But ∠ DAL = 15° . Thus LD = LA. We hence have LD = LA = LB . This implies that L is circumcentre of the triangle BDA . Thus∠BAD = 1/2∠BLD = 1/2 x 60 = 30°
Related Solutions
In Delta ABC, let D be the mid point of BC. If /_ADB=45^(@) and /_ACD=30^(@) then determine /_BAD
View Solutionदी गई आकृति में और का मध्य बिंदु हैं।
क्या है ? कारण दीजिए।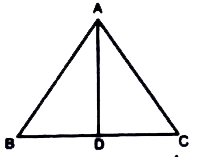
View SolutionIn the triangle ABC, D is on BC angle ADB =90^@, angle ABC =45^@ , AD= 10cm, AC = 20 cm. then BC is equal to:
View SolutionIn triangle , if is point on such that then
View SolutionDelta ABC In BC, D is the midpoint of BC, E is the midpoint of BD and O is the midpoint of AE. Then, ar( Delta BOE) = ?
View SolutionLet ABC be an acute-angled triangle and let D be the midpoint of BC. If AB = AD, then tan(B)/tan(C) equals
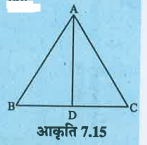
View Solutionआकृति 7.15 में AB=AC और D, का मध्य बिंदु है। क्या है? कारण दीजिए ।
View Solutionदी गई आकृति में और का मध्य बिंदु हैं।
क्या है ? कारण दीजिए।
View Solutionमाना ABCD एक चतुष्फलक इस प्रकार है कि भुजायें AB,AC तथा AD परस्पर लम्बवत है। माना त्रिभुजों ABC, ACD तथा ADB के क्षेत्रफल क्रमशः 3,4,5 है तो त्रिभुज BCD का क्षेत्रफल है: (i) (ii) (iii) (iv)
View Solution-এর AC=BC এবং BC বাহুকে D পর্যন্ত বর্ধিত করলাম। যদি হয়, তবে ABC ত্রিভুজের প্রতিটি কোণের বৃত্তীয় মান নির্ণয় করো।
View SolutionIn Fig. 9.29 ratio of the area of triangle ABC to the area of triangle ACD is the same as the ratio of base BC of triangle ABC to the base CD of triangle ACD.
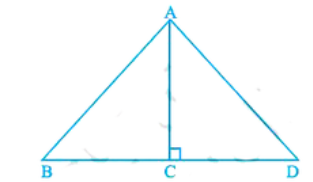
View SolutionABC is an isosceles triangle with AB = AC and D is on side BC such that AD _|_ BC Is. angle BAD = angle CAD To prove it, a student followed the following procedure: Delta ABD And Delta ACD In, AB = AC (Given) angle B = angle C (Because AB = AC) And angle ADB = angle ADC (each 90^(@) , Therefore, Delta ABD ~= Delta ACD (A AS) So, angle BAD = angle CAD (CPCT) What is missing in the above arguments?
View Solutionमें, पर बिंदु इस प्रकार है कि और हैI की माप ज्ञात करेंI
View Solutionत्रिभुज ABC में, , D, भुजा AC का मध्य-बिंदु है, तथा AB व BC का योग 30 सेमी है, तो त्रिभुज ABC का क्षेत्रफल ज्ञात कीजिये।
View SolutionIn a triangle is the midpoint of . Sum of sides of AB & BC is 30 cm. Find the area of triangle ABC.
View SolutionABC ত্রিভুজের পরিকেন্দ্র O এবং D বিন্দু BC বাহুর মধ্যবিন্দু। হলে, -এর মান নির্ণয় করো ।
View SolutionIf D is the midpoint of the side BC of ABC then
View SolutionABC is a right angled triangle with angleS=90^@ .If D is the midpoint of BC, then
View SolutionIn Delta ABC, D is the midpoint of bar(BC) . bar(AD) is the _______________
View SolutionIn Delta ABC, D is the midpoint of bar(BC) . bar(AE) is the ______________
View Solution