Let ABC be an acute-angled triangle and let D be the midpoint of BC. If AB = AD, then tan(B)/tan(C) equals
√2
√3
2
3
The correct Answer is:D
Step by step video, text & image solution for Let ABC be an acute-angled triangle and let D be the midpoint of BC. If AB = AD, then tan(B)/tan(C) equals by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUESTION PAPER 2013BOOK - KVPY PREVIOUS YEARCHAPTER - QUESTION PAPER 2013EXERCISE - PART-II ( MATHEMATICS)
10 Videos
- QUESTION PAPER 2013BOOK - KVPY PREVIOUS YEARCHAPTER - QUESTION PAPER 2013EXERCISE - PART-II (MATHEMATICS)
5 Videos
- MOCK TEST 9BOOK - KVPY PREVIOUS YEARCHAPTER - MOCK TEST 9EXERCISE - EXERCISE
25 Videos
- QUESTION PAPER 2020BOOK - KVPY PREVIOUS YEARCHAPTER - QUESTION PAPER 2020EXERCISE - PART-II(MATHEMATICS)
10 Videos
Similar Questions
Knowledge Check
Let ABC be an acute-angled triangle and let D be the midpoint of BC. If AB = AD, then tan(B)/tan(C) equals
A√2B√3C2D3Let ABC be an acute angled triangle and CD be the altitude through C. If AB = 8 cm and CD = 6 cm, then the distance between the midpoints AD and BC is :
A6B4C4.5D5ABC is right angled triangle, right angled at C . D is the midpoint of BC. Then , tanθtanϕ =
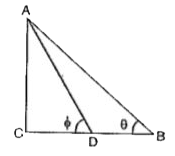 A1B1√2C12D2
A1B1√2C12D2
ΔABC is an acute angled triangle. CD be the altitude through C. If AB=8,CD=6 , then the distance between the mid-points of AD and BC is
View SolutionLet ABC be an equilateral triangle. If the side BC is produced to the point D so that BC = 2CD, then AD2 is equal to
View SolutionIf A, B, C be an acute angled triangle, then the minimum value of tan4A+tan4B+tan4C will be
View SolutionLet ABC be an equilateral triangle. Let BE⊥CA meeting CA at E, then (AB2+BC2+CA2) is equal to :
View SolutionIn an acute-angled triangle ABC if sin (B+C−A)=√32 and tan(C+A−B)=1, then C is equal to
View Solution
