Consider a triangle ABC in the xy -plane with vertices A = (0,0), B = (1,1) and C = (9, 1). If the line x = a divides the triangle into two parts of equal area, then a equals
3
3.5
4
4.5
The correct Answer is:A
To find the value of a that divides triangle ABC into two parts of equal area, we can follow these steps:
Step 1: Calculate the Area of Triangle ABC
The vertices of the triangle are given as:
- A(0,0)
- B(1,1)
- C(9,1)
The area A of a triangle can be calculated using the formula:
Area=12×base×height
In this triangle:
- The base BC can be considered as the horizontal distance between points B and C, which is 9−1=8.
- The height from point A to line BC is 1 (the y-coordinate of points B and C).
Thus, the area of triangle ABC is:
Area=12×8×1=4 square units
Step 2: Find Half of the Area
Since we want to divide the triangle into two equal areas, we need half of the total area:
Half Area=42=2 square units
Step 3: Set Up the Equation for Area of the New Triangle
We need to find the line x=a that divides the triangle into two parts of equal area. The area of the triangle formed by points A(0,0), B(1,1), and the intersection point on line x=a can be calculated.
The height of the triangle formed will be the vertical distance from line BC to point A, which is given by:
Height=1−a9
The base of this new triangle will be:
Base=9−a
Step 4: Write the Area Equation
The area of the new triangle can be expressed as:
Area=12×Base×Height=12×(9−a)×(1−a9)
Setting this equal to 2 (the half area):
12×(9−a)×(1−a9)=2
Step 5: Simplify and Solve for a
Multiply both sides by 2:
(9−a)×(1−a9)=4
Expanding the left side:
(9−a)(1−a9)=9−a−9a9+a29=9−a−a+a29=9−2a+a29
Setting this equal to 4:
9−2a+a29=4
Rearranging gives:
a29−2a+5=0
Multiplying through by 9 to eliminate the fraction:
a2−18a+45=0
Step 6: Use the Quadratic Formula
Using the quadratic formula a=−b±√b2−4ac2a:
Here, a=1,b=−18,c=45:
a=18±√(−18)2−4⋅1⋅452⋅1
=18±√324−1802
=18±√1442
=18±122
Calculating the two possible values:
1. a=302=15
2. a=62=3
Since a must be between 0 and 9 (the x-coordinates of points A and C), we take:
a=3
Final Answer
Thus, the value of a that divides the triangle into two equal areas is:
3
The vertices of the triangle are given as:
- A(0,0)
- B(1,1)
- C(9,1)
Area=12×base×height
- The base BC can be considered as the horizontal distance between points B and C, which is 9−1=8.
- The height from point A to line BC is 1 (the y-coordinate of points B and C).
Area=12×8×1=4 square units
Since we want to divide the triangle into two equal areas, we need half of the total area:
Half Area=42=2 square units
We need to find the line x=a that divides the triangle into two parts of equal area. The area of the triangle formed by points A(0,0), B(1,1), and the intersection point on line x=a can be calculated.
Height=1−a9
The base of this new triangle will be:
Base=9−a
The area of the new triangle can be expressed as:
Area=12×Base×Height=12×(9−a)×(1−a9)
12×(9−a)×(1−a9)=2
Multiply both sides by 2:
(9−a)×(1−a9)=4
(9−a)(1−a9)=9−a−9a9+a29=9−a−a+a29=9−2a+a29
9−2a+a29=4
a29−2a+5=0
a2−18a+45=0
Using the quadratic formula a=−b±√b2−4ac2a:
Here, a=1,b=−18,c=45:
a=18±√(−18)2−4⋅1⋅452⋅1
=18±√324−1802
=18±√1442
=18±122
1. a=302=15
2. a=62=3
a=3
Thus, the value of a that divides the triangle into two equal areas is:
3
Topper's Solved these Questions
- QUESTION PAPER 2013BOOK - KVPY PREVIOUS YEARCHAPTER - QUESTION PAPER 2013EXERCISE - PART-II ( MATHEMATICS)
10 Videos
- QUESTION PAPER 2013BOOK - KVPY PREVIOUS YEARCHAPTER - QUESTION PAPER 2013EXERCISE - PART-II (MATHEMATICS)
5 Videos
- MOCK TEST 9BOOK - KVPY PREVIOUS YEARCHAPTER - MOCK TEST 9EXERCISE - EXERCISE
25 Videos
- QUESTION PAPER 2020BOOK - KVPY PREVIOUS YEARCHAPTER - QUESTION PAPER 2020EXERCISE - PART-II(MATHEMATICS)
10 Videos
Similar Questions
Knowledge Check
If a △ABC has vertices (0,0), (11,60) and (91,0). If the line y=kx cuts the triangle into two triangles of equal area , then k is equal to
A3051B47C74D3091The area of ΔABC with vertices A (2,1), B(3,4) and C (0.5) is
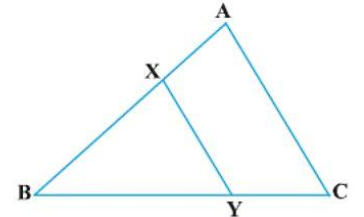
A1 sq. unitsB2 sq. unitsC3 sq. unitsD4 sq. unitsIn Figure the line segment XY is parallel to side AC of ΔABCand it divides the triangle into two parts of equal areas. Find the ratio AXAB.
A√2+1+√2B2−√2:2C1:√2D1:1
Consider the ΔABC with vertices A(−2,3),B(2,1)andC(1,2). what is the foot of the altitude from the vertex A of the triangle ABC?
View SolutionIn Figure the line segment XY is parallel to side AC of ΔABCand it divides the triangle into two parts of equal areas. Find the ratio AXAB.
View SolutionThe area of the triangle whose vertices are A(1,2−1) B (3,1,4) and C (0,2,3)
View SolutionConsider the ΔABC with vertices A( - 2 , 3) , B (2 , 1) and C (1 ,2)
What is the Centroid of the ΔABC ?
View SolutionConsider the ΔABC with vertices A( - 2 , 3) , B (3 , 1) and C (1 ,2)
What is the centroid of the ΔABC ?
View Solution
