In a triangle ABC points X and Y are on AB and AC respectively such that XY is parallel to BC. Which of the two following equalities always hold ? Here [PQR] denotes the area of triangle PQR -I [BCX] = [BCY]II [ACX].[ABY] = [AXY].[ABC] A Neither I nor II B I only C II only D Both I and II
Correct option D Both I and IIExplanation:Clearly ar BCX = ar BCY {Δs between parallel lines & same base} [BCX] = [BCY]I is true.CheckII ar ΔACX = 1/2 AC.AX sin A arΔABY = 1/2 AB.AY sin A.ar ΔAXY = 1/2 AX.AY sin A arΔABC = 1/2 AB.AC sin A.Clearly [ACX].[ABY] = [AXY].[ABC]II is true
Related Solutions
in a triangle ABC , points X and Y are on AB And AC , respectively , such that XY is parallel to BC . Which of the two following equalities always hold? (here [PQR] denotes the area of triangle PQR).
(i) [BCX]=[BCY]
(ii)
View SolutionIf and are two triangles such that are respectively equal and parallel to then show that (i) quad ABED is a parallelogram (ii) quad BCFE is a paralellogram (iii) AC=DF (iv)
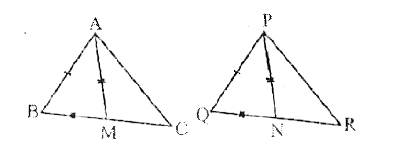
View SolutionTwo sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of PQR. Show that
(ii)
View Solutionयदि AD तथा PM क्रमशः तथा के समद्विभाजक है जहाँ है तो सिद्ध कीजिए कि :
(i)
(ii)
View Solutionएक त्रिभुज ABC की दो भुजाओ AB और AC तथा माध्यिका AM क्रमश: एक दूसरे त्रिभुज की भुजाओ PQ और QR तथा माध्यिका PN के बराबर है (आकृति देखिये) दर्शाइए की
(i)
(ii)

View Solution, में, किरण AD, को समद्विभाजित करती है तथा BC को बिंदु D पर प्रतिच्छेद करती है। यदि BC = a, AC = b तथा AB =c हो, तो सिद्ध कीजिए कि -
|
View Solutionसमद्विबाहु में यदि तथा एवं ऊंचाई हो, तो समद्विबाहु त्रिभुज का क्षेत्रफल बराबर है।
View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that, (i) AD bisects BC (ii) AD bisects
View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that, (i) AD bisects BC (ii) AD bisects
View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that, (i) AD bisects BC (ii) AD bisects
View SolutionAD is an altiude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC (ii) AD bisects A.
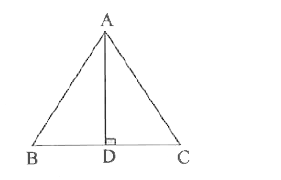
View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that, (i) AD bisects BC (ii) AD bisects
View SolutionIn a triangle ABC, D is mid-point of BC; AD is produced upto E so that DE = AD Prove that: (i) triangle ABD and triangle ECD are congruent. (ii) AB = EC. (ii) AB is parallel to EC
View Solutiontriangle ABC ରେ AB =.5 ସେ.ମି., BC = 7 ସେ.ମି. ଓ CA = ୨ ସେ.ମି. I triangle ABC ~ triangle PQR I triangle PQR ର ପରିସୀମା 63 ସେ.ମି. ହେଲେ PQ ର ଦୈର୍ଘ୍ୟ କେତେ ସେ.ମି. ?
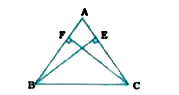
View SolutionABC ਇੱਕ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸ ਵਿਚ ਭੁਜਾਵਾਂ AC ਅਤੇ AB ਉੱਤੇ ਸਿਖਰਲੰਬ BE ਅਤੇ CF ਬਰਾਬਰ ਹਨ (ਦੇਖੋ ਚਿੱਤਰ 7.32)। ਸਿੱਧ ਕਰੋ ਕਿ (i) (ii) AB = AC ਜਾਂ ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜ ਹੈ।
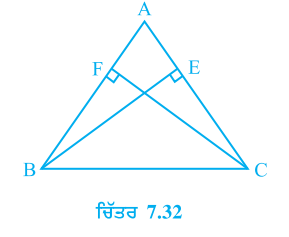
View SolutionABC एक त्रिभुज है जिसमें AC और AB पर खींचे गए शीर्षलम्ब BE और CF बराबर है। दर्शाइए कि
(i)
(ii) , अर्थात एक समद्विबाहु त्रिभुज है।
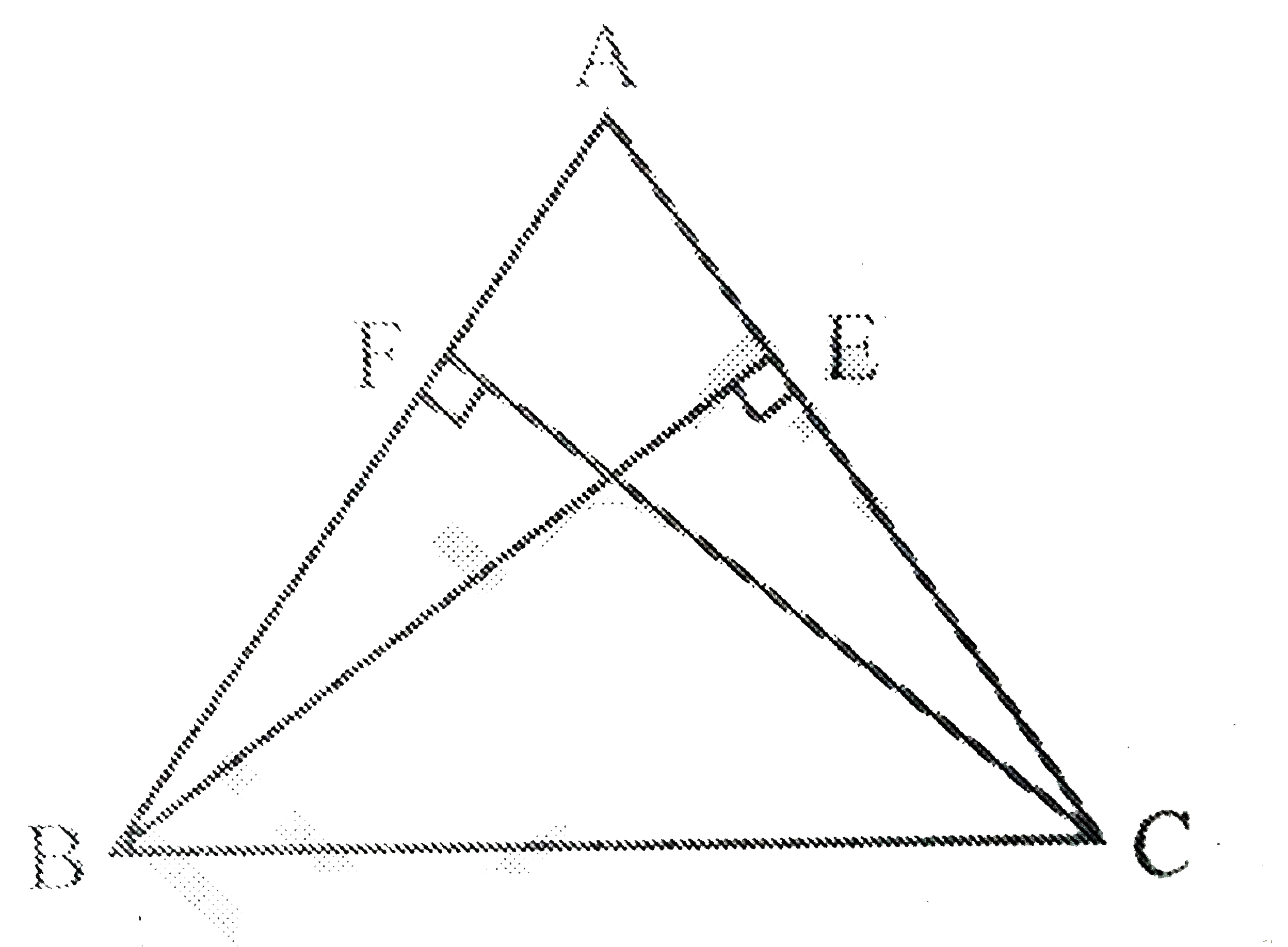
View SolutionIn triangle ABC, AC = 10 cm, BC = 8 cm and AE = 6 cm, then find. (i) Area of triangle ABC (ii) Length of BD
View SolutionABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see the given figure). Show that ( i )
(ii) AB = AC i.e ABC is an isoceles triangle
View SolutionIn triangle A B C and Delta PQR shown below. A B=Q R , BC=RP and C A=P Q i) Are CD and PS equal? Why? ii) What is the relation between the areas of triangle ABC and triangle PQR?
View SolutionD and E are points on sides AB and AC respectively of Delta ABC such that ar( Delta DBC) = ar( Delta EBC). Prove that DE I I BC.
View Solution