A and B are two points on a uniform ring of resistance R the ∠AOB = θ3 where O is the centre of the ring. The equivalent resistance between A and B is. A Rθ/2π B [{R2π – θ}/{4π}] C R[1 – θ/2π] D {R/4π2} 2π – θθ
The correct option D {R/4π2} 2π – θθExplanation:R1 = Resistance of section ADB = rθ × R/2πras for 2πr length resistance is R.& length of arc ADB = rθ∴ R1 = Rθ/2πResistance of ACB R2 = r2π – θ {R/2πr}R2 = [{R2π – θ}/2π]Req = R1 || R2= [{Rθ/2π} × {R2π – θ/2π}/{Rθ/2π} + {R2π – θ/2π}]= [{Rθ2π – θ}/2π2]= [{Rθ2π – θ}/{4π2}]
Related Solutions
Solve rsinθ=3 , r=4(1+sinθ) , 0≤θ≤2π.
View SolutionA and B are two points in a uniform ring of resistance , where C is centre of ring. The equivalent resistance between A and B is :
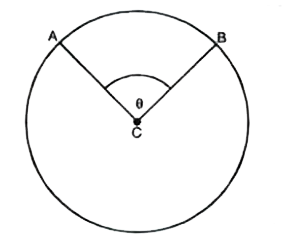
View SolutionIn a uniform ring of resistance R there are two points A and B such that /_ ACB = theta , where C is the centre of the ring. The equivalent resistance between A and B is
View SolutionIn a uniform ring of resistance there are two points and such that , where is the centre of the ring. The equivalent resistance between and is
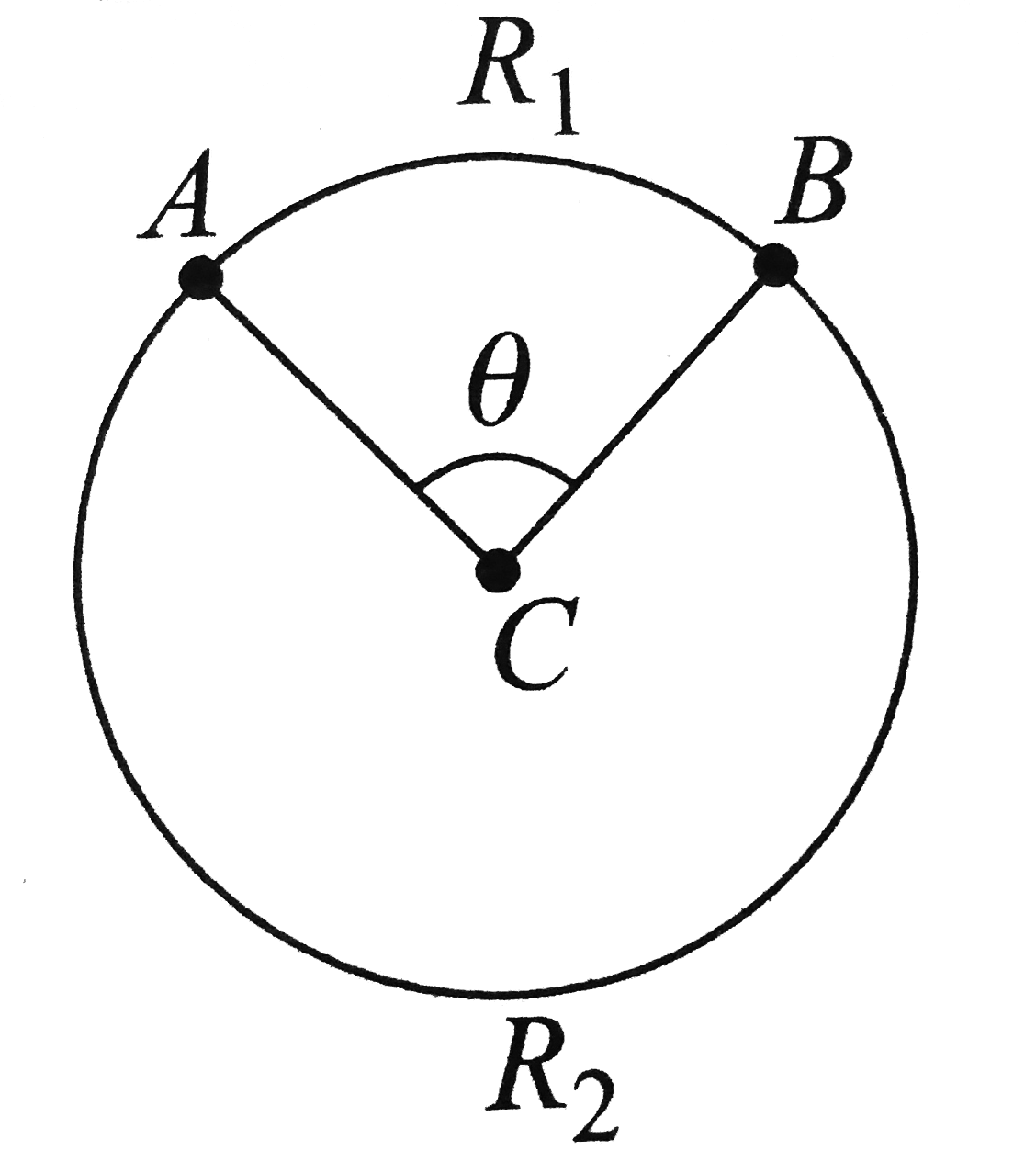
View Solutionand are two points on a uniform ring of resistance . The , where is the center of the ring. The equivalent resistance between and is.
View SolutionA and B are two points on a uniform ring of radius r. The resistance of the ring is R. as shown in the figure. The equivalent resistance between points A & B is _______.
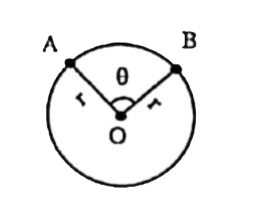
View SolutionA wire is bent in the form fo uniform circular ring. A and B are two points on the ring such that , where O is the centre of ring . If the equivalent resistance cross A and B is 5 . What is the resistance of whole wire
View Solutionand are two points on a uniform ring of resistance the , whre is the centre of the sign. The equivalent reisrtance between and
View SolutionA and B are two points on a circular ring made of uniform wire of resistane R. If the part AB of the ring subtends an angle at the centre C of the ring as shown below, find the resistance of the ring between the points A and B.
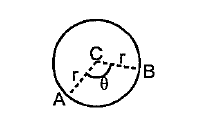
View SolutionA एवं B, प्रतिरोध की एकसमान वलय पर दो बिन्दु हैं। एवं B के मध्य तुल्य प्रतिरोध है
View SolutionGiven and (3π)/2<θ<2π then Find the other Trigonometric function of the angle θ.
View SolutionIf ytan(θ− π/6)=xtan(θ+ 2π/3) , then (y+x)/(y-x) =
View SolutionP and Q are two points on a uniform ring of resistance R. The equivalent resistance between P and Q is
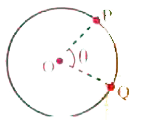
View SolutionA and B are two points on a uniform ring of resistance . The The equivalent resistance between A and B is
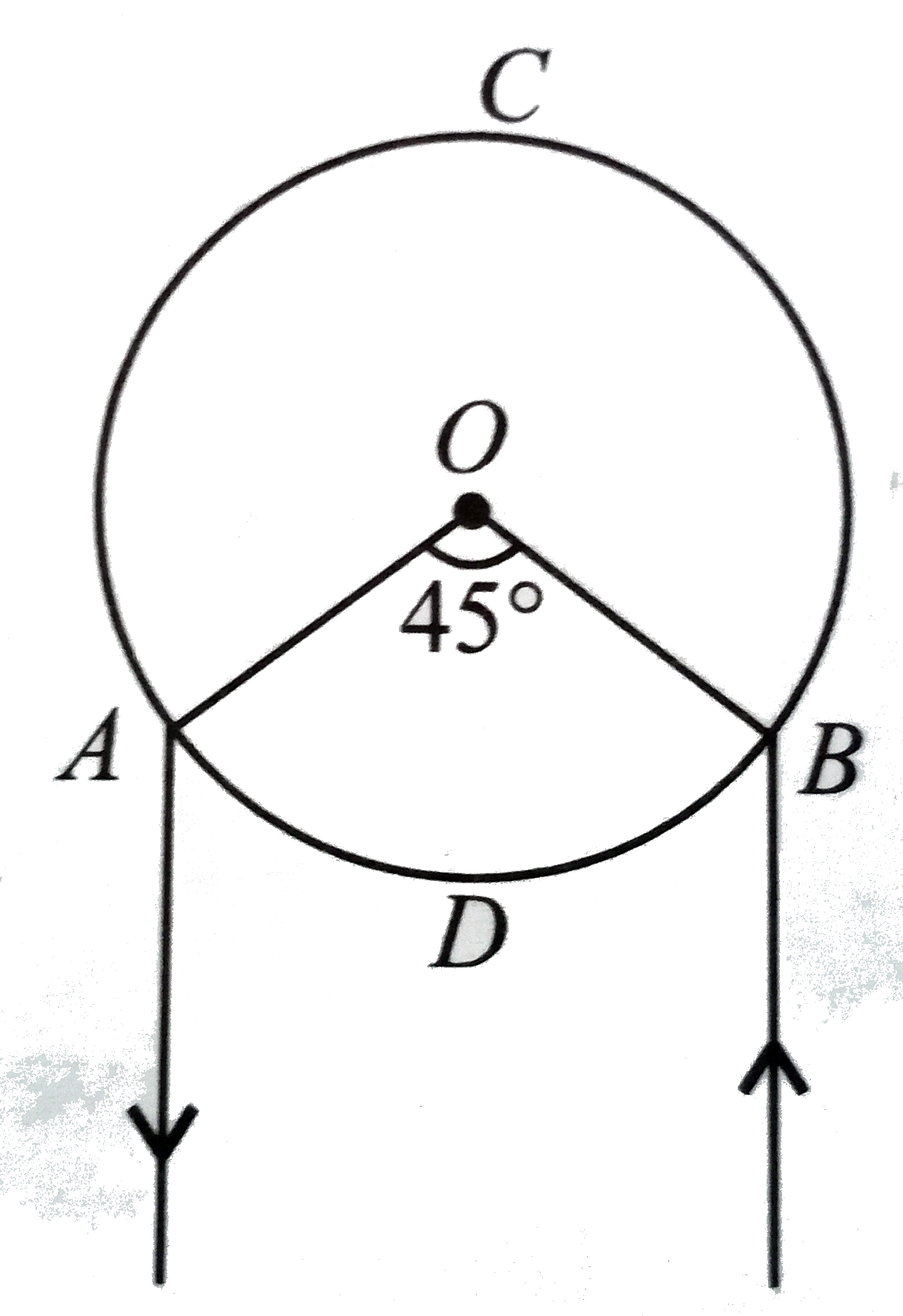
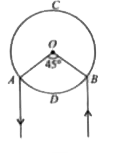
View SolutionA and B are two points on a uniform ring of resistance 15Omega . The ltAOB=45^(@) The equivalent resistance between A and B is
View SolutionA and B are two points on a uniform ring of resistance 15Omega . The ltAOB=45^(@) The equivalent resistance between A and B is
View Solutionएक बैटरी त्रिज्या r और प्रतिरोध R के एकसमान चालक वलय की परिधि पर दो बिंदुओं A और B के बीच जुड़ी हुई है। वलय के चापों में से एक AB केंद्र पर कोण अंतरित करता है। वलय में धारा के कारण केंद्र पर चुंबकीय प्रेरण का मान है
View SolutionA solenoid has 1000 turns per meter length. If a current of 5A is flowing through it. then magnetic field inside the solenoid is (a) 2π X 10^-3 T (b) 2π X10^-5 T (c) 4π X 10^-3 T (d) 4π X 10^-5T
View SolutionA solenoid has 1000 turns per meter length. If a current of 5A is flowing through it. then magnetic field inside the solenoid is (a) 2π X 10^-3 T (b) 2π X10^-5 T (c) 4π X 10^-3 T (d) 4π X 10^-5T
View SolutionA solenoid has 1000 turns per meter length. If a current of 5A is flowing through it. then magnetic field inside the solenoid is (a) 2π X 10^-3 T (b) 2π X10^-5 T (c) 4π X 10^-3 T (d) 4π X 10^-5T
View Solution