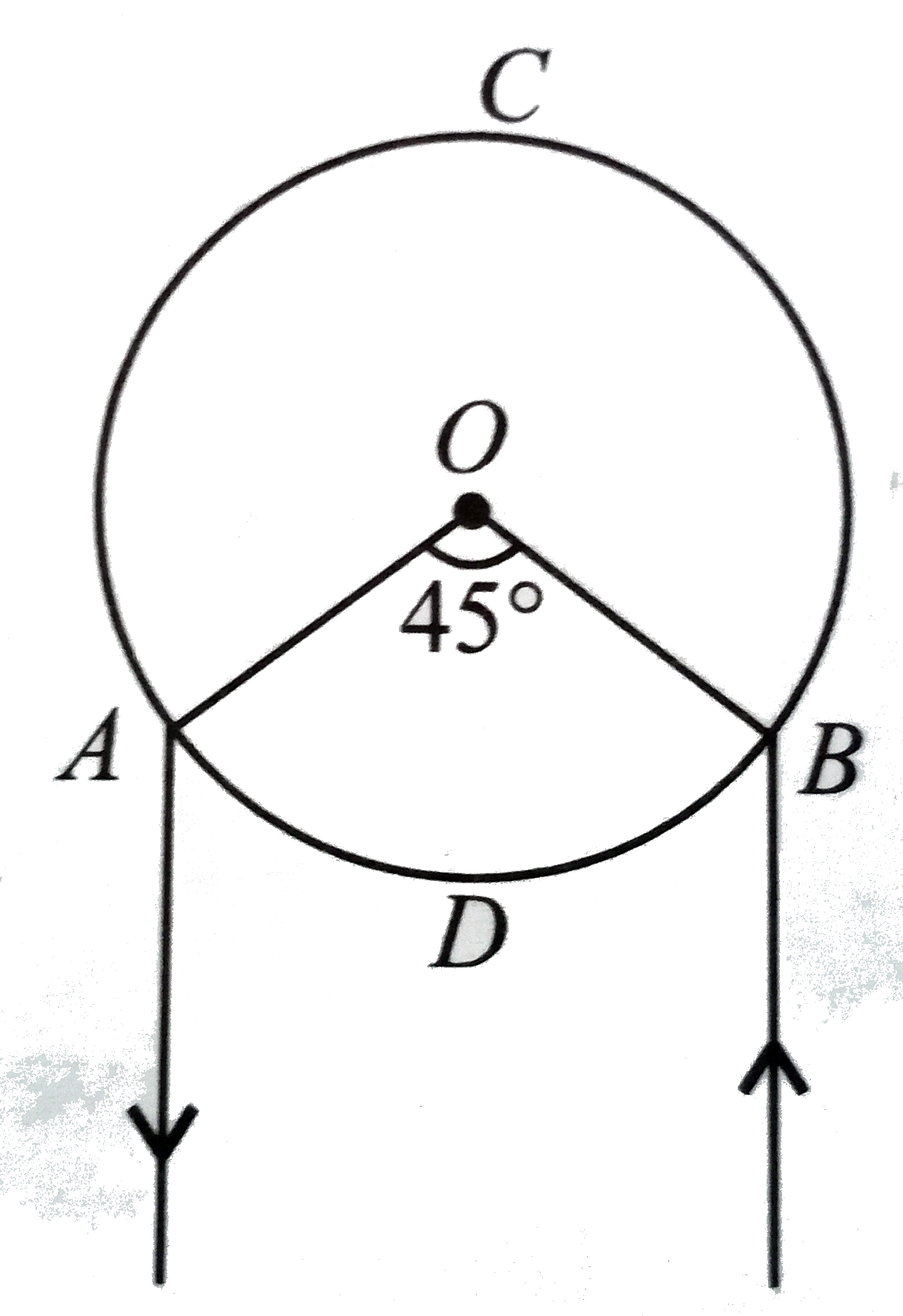
A and B are two points on a uniform ring of resistance 15Ω. The <AOB=45∘ The equivalent resistance between A and B is
A
1.64Ω
B
2.84Ω
C
4.57Ω
D
2.64Ω
Video Solution
Text Solution
The correct Answer is:A
Resistance per unit length of ring, ρ=R2πr
Length of sections ADB and ACB are rθandr(2π−θ)
∴ Resistance of section ADB: R1=ρrθ
=R2πrrθ=Rθ2π
and resistance of section ACB, R2=ρr(2π−θ)
=R2πrr(2π−θ)=R(2π−θ)2π
Now, R1andR2 are connected in parallel between A and B then
Req=R1R2R1+R2=Rθ2π×R(2π−θ)2πRθ2π+R(2π−θ)2π
Rθ×R(2π−θ)(2π)2Rθ+R(2π−θ)2π=Rθ(2π−θ)4π2
Putting θ=45∘=π4 rad and R=15Ω
Req=15×π4×(2π−π4)4π2=15π4(7π4)4π2
=10564Ω=1.64Ω
|
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:PHYSICS WALLAHChapter:CURRENT ELECTRICITYExercise:NEET Past 5 Years Questions
Explore 23 Videos
- CURRENT ELECTRICITYBook:PHYSICS WALLAHChapter:CURRENT ELECTRICITYExercise:NEET Past 5 Years Questions
Explore 23 Videos
- ALTERNATING CURRENT Book:PHYSICS WALLAHChapter:ALTERNATING CURRENT Exercise:NEET PAST 5 YEARS QUESTIONS
Explore 8 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:PHYSICS WALLAHChapter:DUAL NATURE OF RADIATION AND MATTERExercise:Neet past 5 years questions
Explore 16 Videos
Similar Questions
Knowledge Check
A and B are two points on a uniform ring of resistance 15Ω. The <AOB=45∘ The equivalent resistance between A and B is
 A1.64ΩB2.84ΩC4.57ΩD2.64Ω
A1.64ΩB2.84ΩC4.57ΩD2.64ΩEquivalent resistance between A and B will be
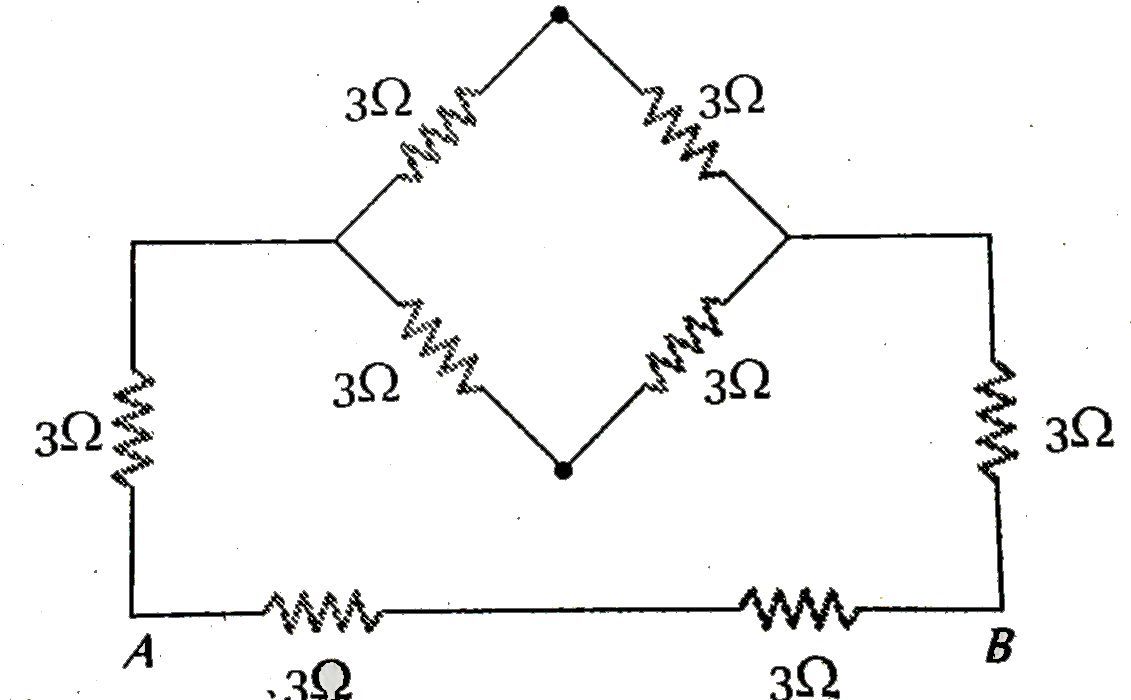 A2 ohmB18 ohmC6 ohmD3.6 ohm
A2 ohmB18 ohmC6 ohmD3.6 ohm
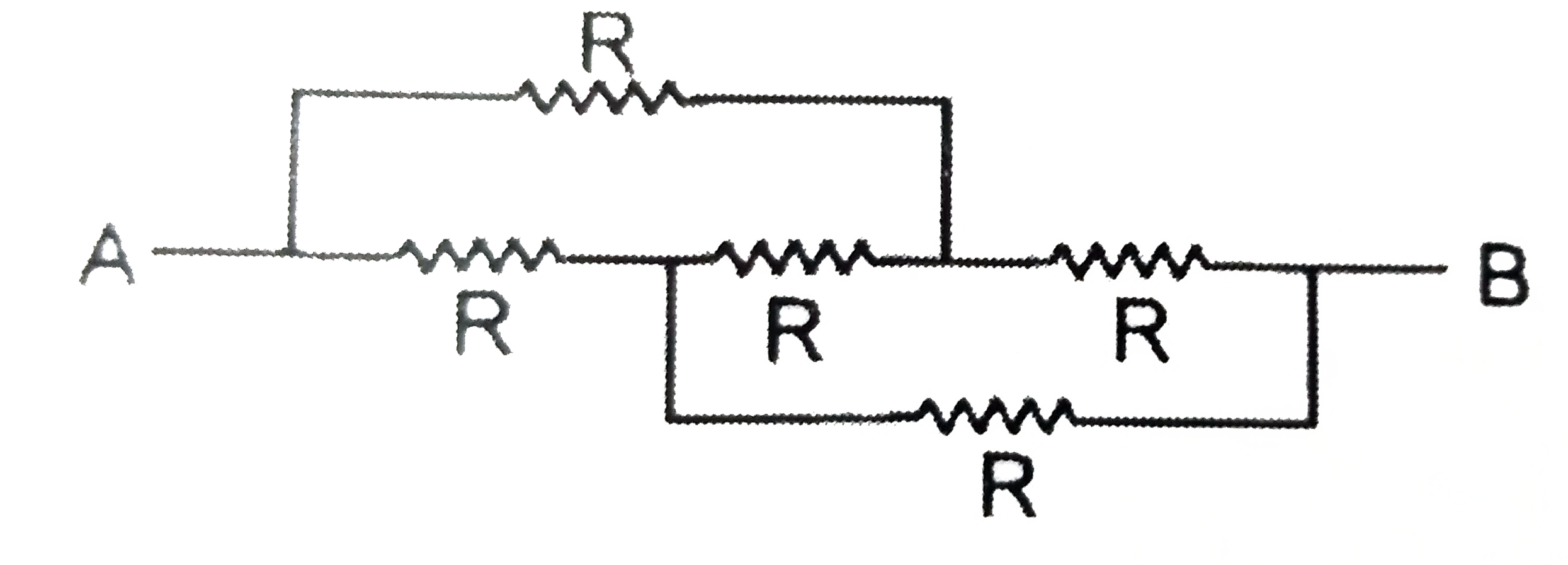
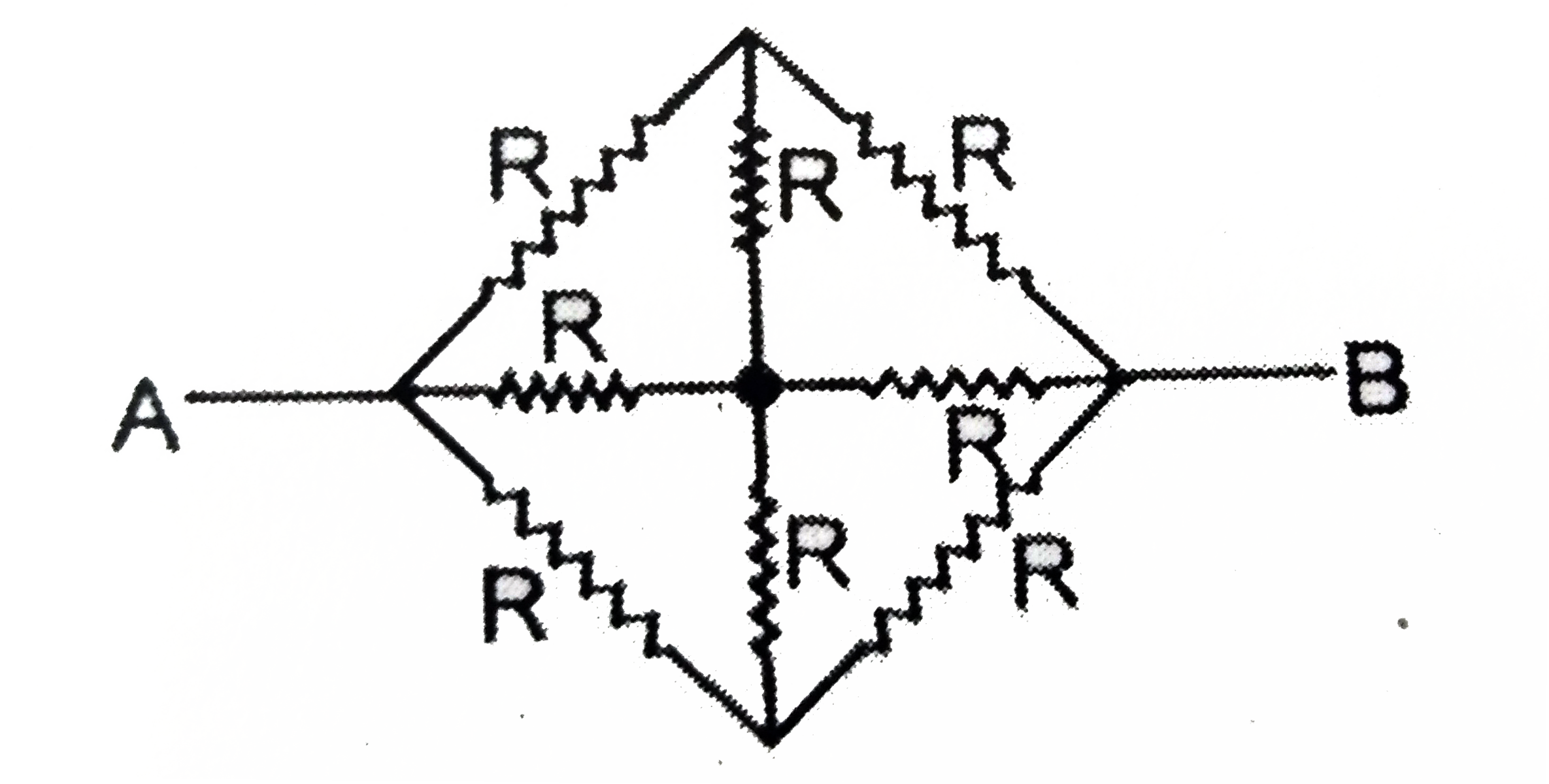
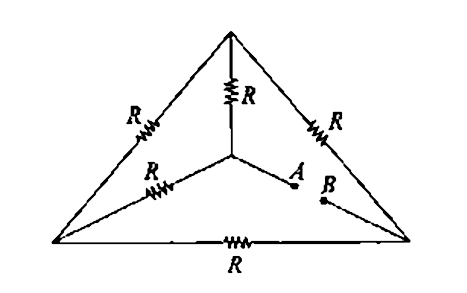
Find the equivalent Resistance between A and B
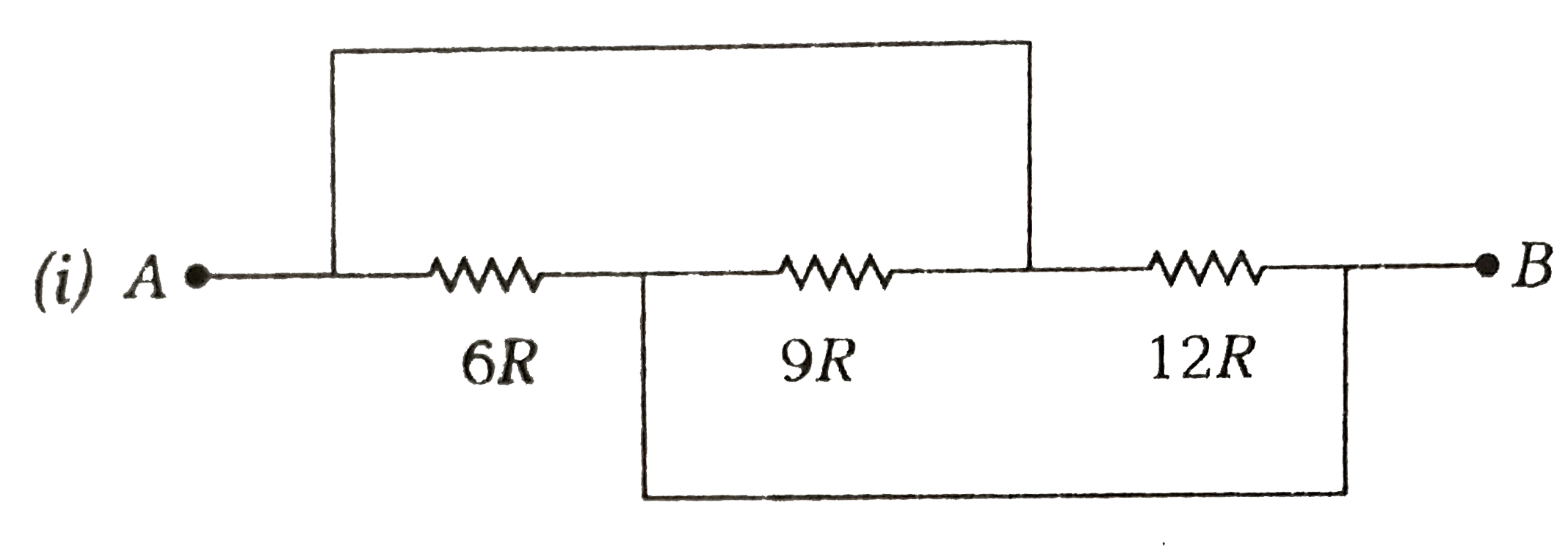
View SolutionFind the equivalent resistance between A and B.
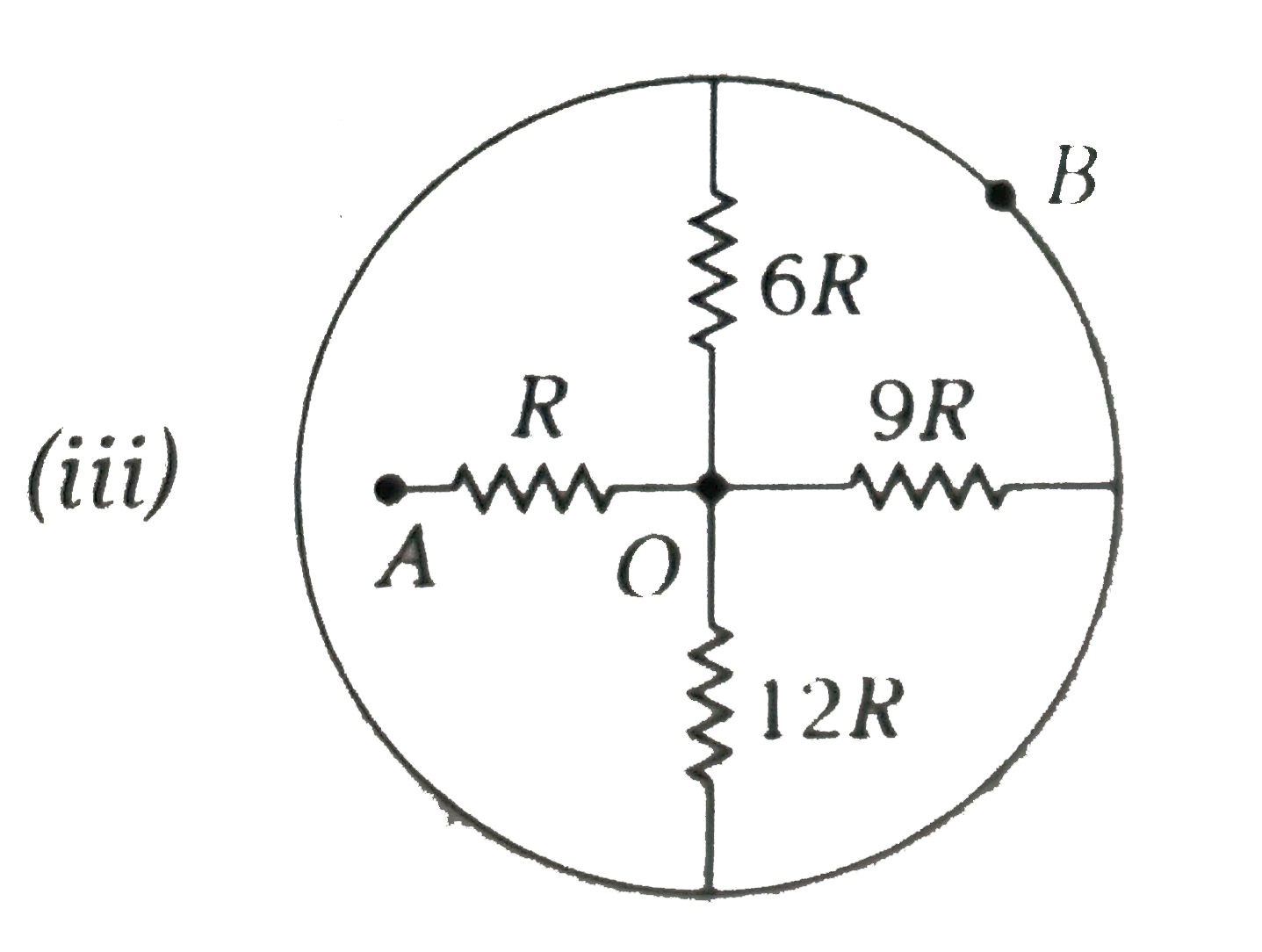
View SolutionFind the equivalent resistance between A and B.
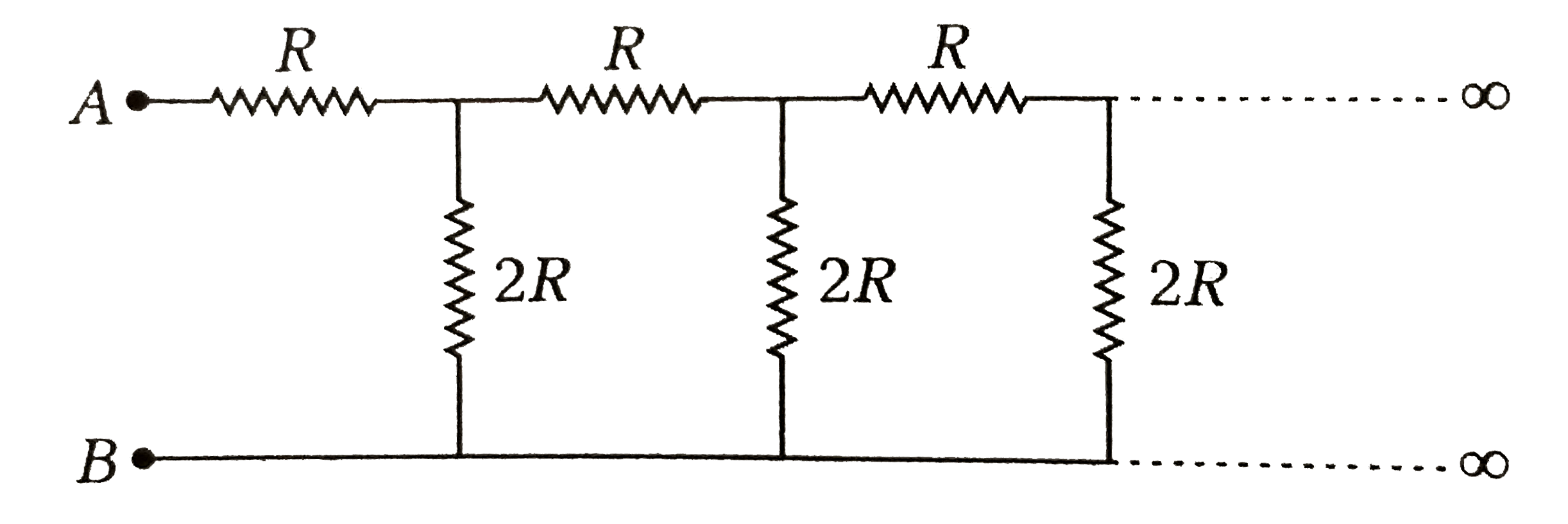
View SolutionFind the equivalent Resistance between A and B
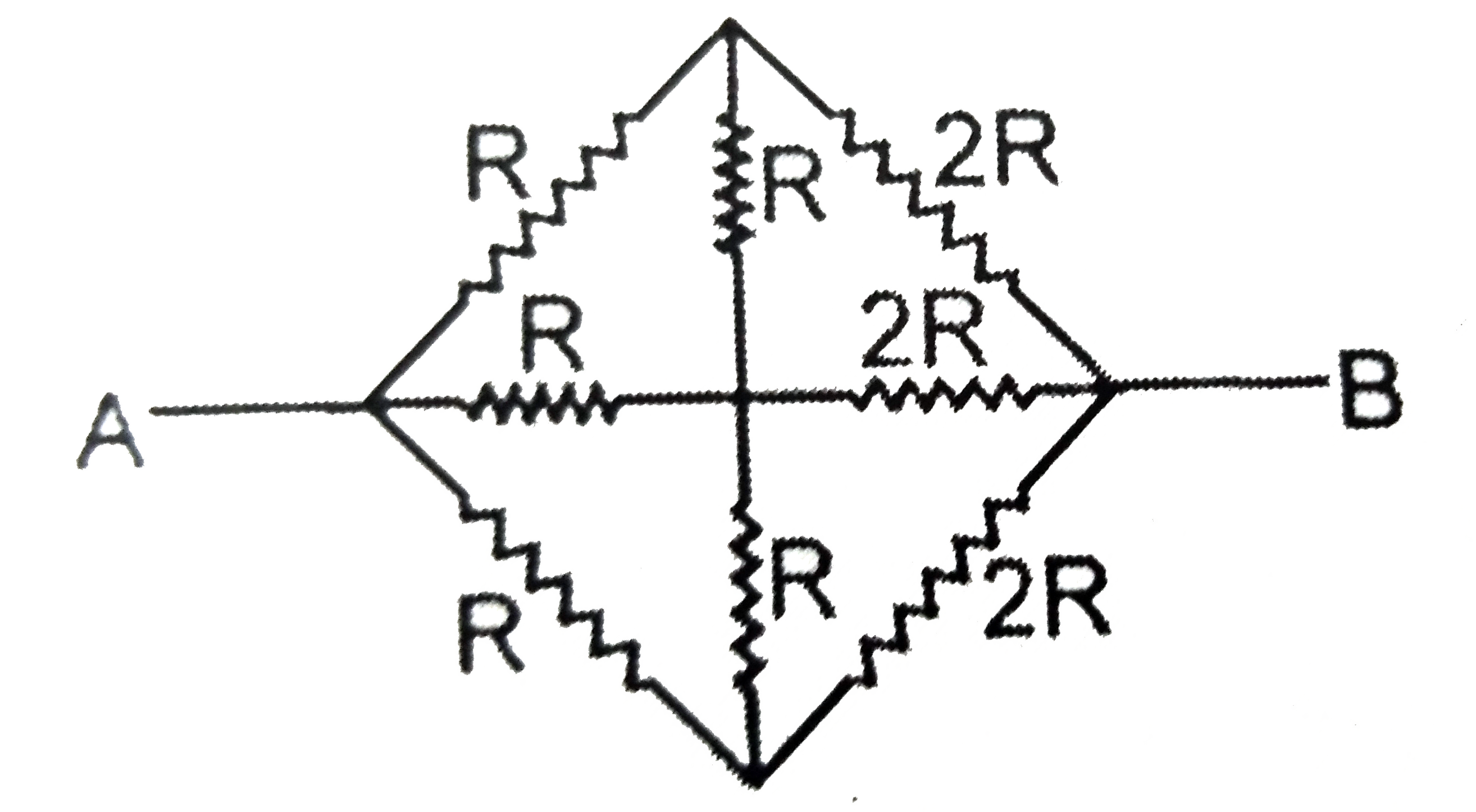
View SolutionFind the equivalent Resistance between A and B
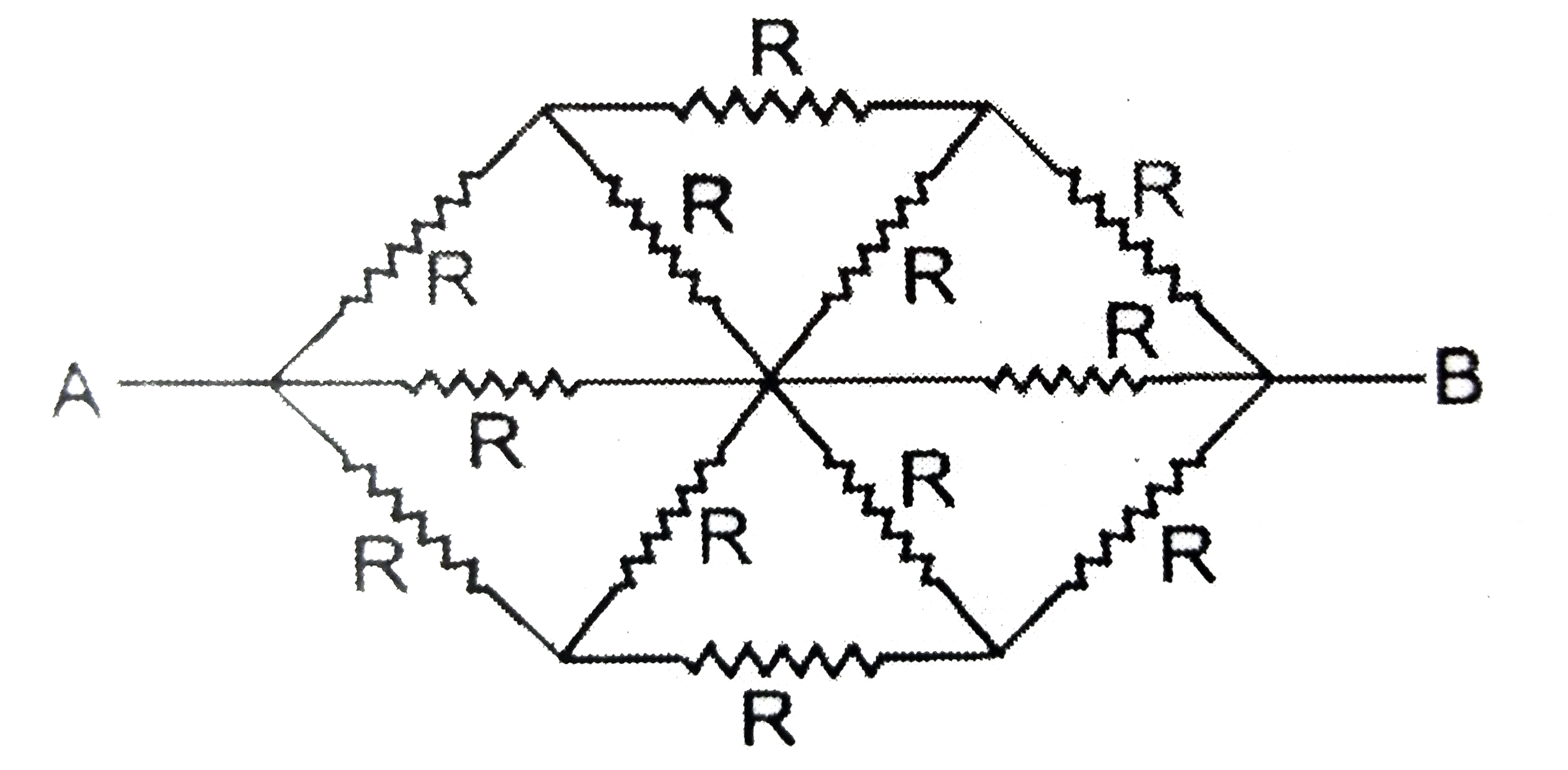
View SolutionFind the equivalent Resistance between A and B
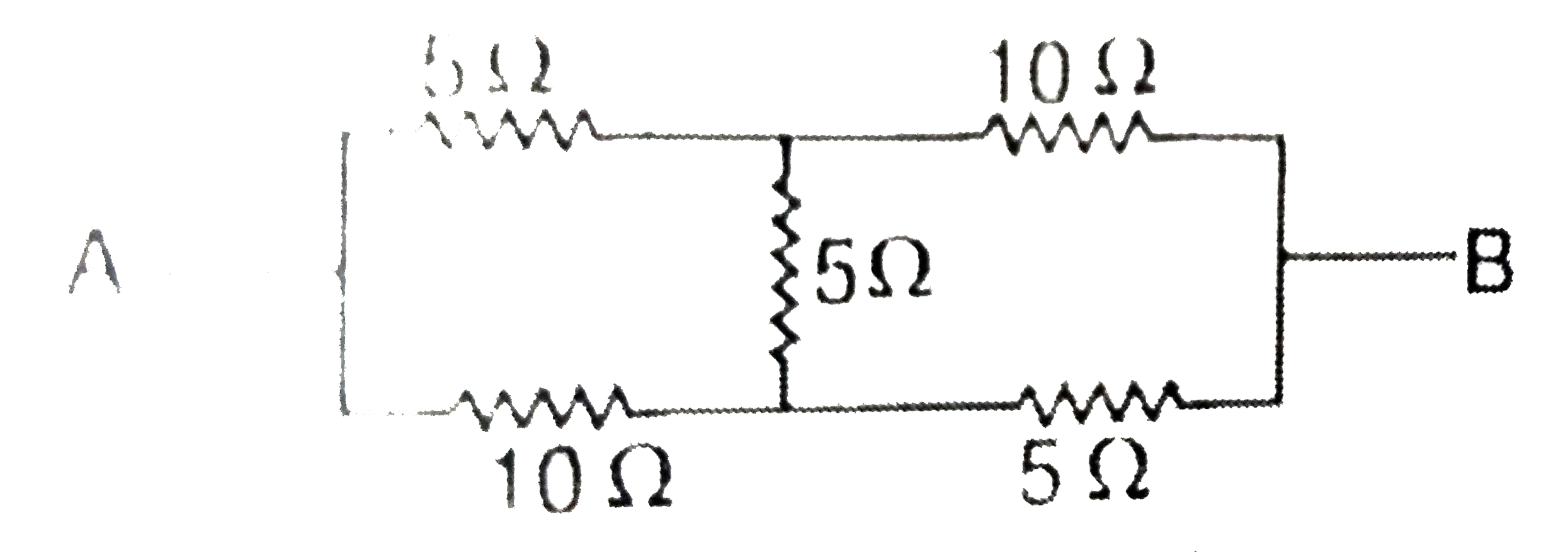
View Solution