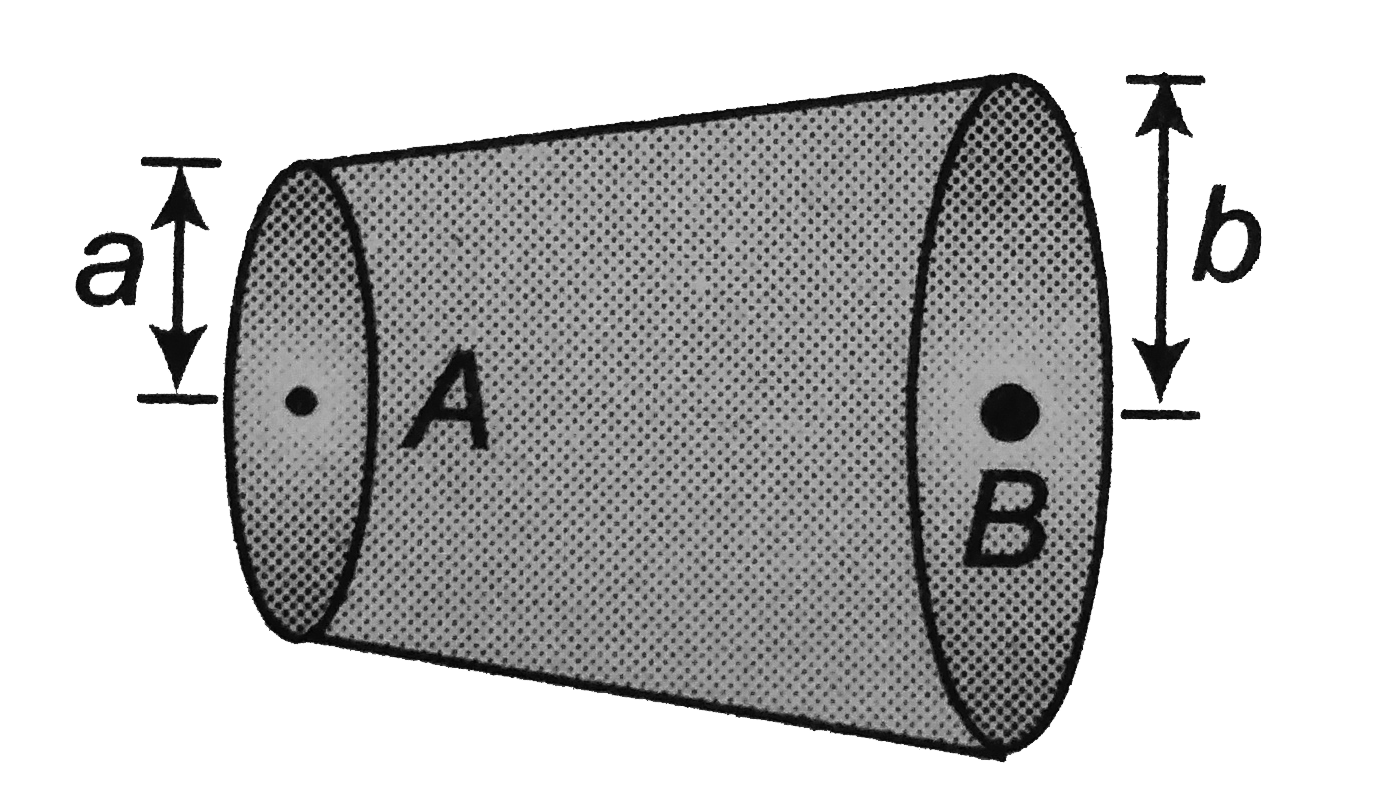
Consider the figure, cross-sectional area of consider at A and B is 2a and a respectively. Current density at A and B are given by JA and JB then JA/JB is

12
2
1
4
The correct Answer is:A
Current flowing through the resistor will be same throughout & J∝IA
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - PHYSICS WALLAHCHAPTER - CURRENT ELECTRICITYEXERCISE - NEET Past 5 Years Questions
23 Videos
- CURRENT ELECTRICITYBOOK - PHYSICS WALLAHCHAPTER - CURRENT ELECTRICITYEXERCISE - NEET Past 5 Years Questions
23 Videos
- ALTERNATING CURRENT BOOK - PHYSICS WALLAHCHAPTER - ALTERNATING CURRENT EXERCISE - NEET PAST 5 YEARS QUESTIONS
8 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - PHYSICS WALLAHCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Neet past 5 years questions
16 Videos
Similar Questions
What is the current in a wire of radius R = 2.67 mm if the magnitude of the current density is given by (a) Jn=J0r/Rand(b)Jb=J0(1−r/R), in which r is the radial distance and J0=5.50×104A/m2? (c) Which function maximizes the current density near the wire's surface?
View SolutionIf the position vectors of A,B,C and D are 2i+j,i−3j,3i+2jandi+λj respectively and ¯¯¯¯¯¯AB∣∣¯¯¯¯¯¯CD ,then λ will be
View Solution
Knowledge Check
If the position vectors of four points A,B,C and D are i+j+k, 2i+3j, 3i+5j-2k and k-j respectively,then AB and CD are related as
AperpendicularBparallelCindependentDNone of the aboveA electric current passes through non uniform cross-section wire made of homogeneous and isotropic meterial. If the jA and JB be the current densities and EA and EB be the electric field intensities at A and B respectively, then
 Aja>jB,EA>EBBja>jB,EA<EBCja<jB,EA>EBDja<jB,EA<EB
Aja>jB,EA>EBBja>jB,EA<EBCja<jB,EA>EBDja<jB,EA<EBFigure shows crosssection view of a infinite cylindrical wire with a cavity, current density is uniform →j=−j0ˆk as shown in figure
 Amagnetic field inside cavity is uniformBmagnetic field inside cavity is along →aCmagnetic field inside cavity is perpendicular to →aDIf an electron is projected with velocity v0ˆj inside the cavity it will move undeviated.
Amagnetic field inside cavity is uniformBmagnetic field inside cavity is along →aCmagnetic field inside cavity is perpendicular to →aDIf an electron is projected with velocity v0ˆj inside the cavity it will move undeviated.
A current is flowing through a cylinderical conductor of radius R, such that current density at any cross-section is given by J=J0(1−rR), where r is radial distance from axis of the cylinder .Calculate the total current through the cross-section of the conductor.
View SolutionA=4i+4j−4kandB=3i+j4k, then angle between vectors A and B is
View SolutionFigure shown variation of magnetic field inside and outside two cylindrical wires P and Q carrying currents that are uniformly distributed across the cross section of wires. If current density for two wires are JP and JQ then

View SolutionIf a=i+j+k and b=i−j+2k then the projection of a on b is given by
View SolutionConsider the vectors a=i−2j+kandb=4i−4j+7k
What is the scalar projection of a on b?
View Solution
