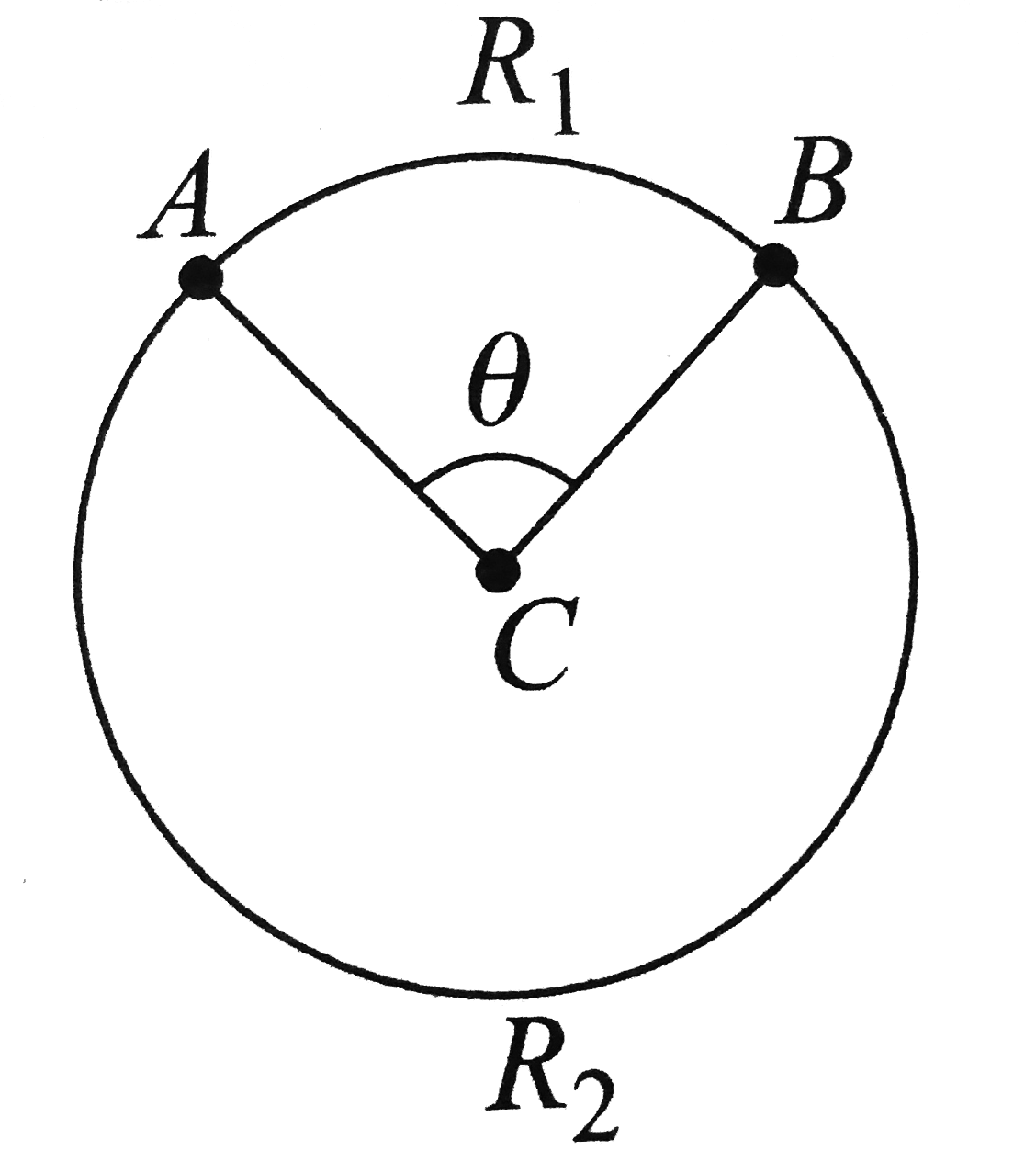
In a uniform ring of resistance R there are two points A and B such that ∠ACB=θ, where C is the centre of the ring. The equivalent resistance between A and B is
A
Rθ2π
B
R(1−θ2π)
C
Rθ(2π−θ)4π2
D
R(2π−θ)4π2
Video Solution
Text Solution
The correct Answer is:C
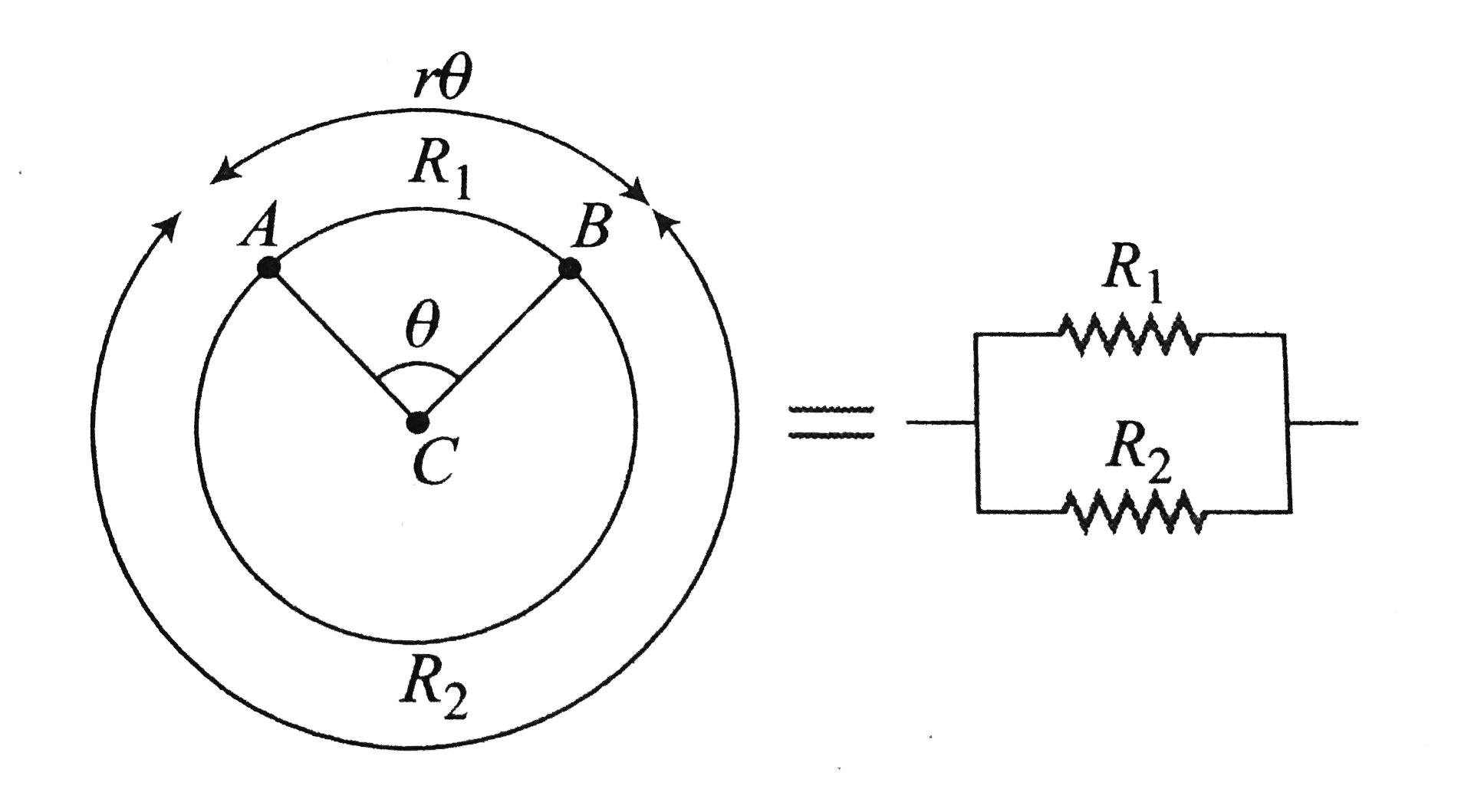
(c ) For ring, the resistance per unit length λ=R2πr
Resistance of sections APB and AQB are
R1=ρrθR2πrrθ=Rθ2π
and R2=R2πrr(2π−θ)=R(2π−θ)2π
As R1 and R2 are in parallel between A and B, their equivalent resistance is
Req=R1R2R1+R2.
=Rθ2π.R(2π−θ)2πRθ2π+R(2π−θ)2π=R2θ(2π−θ)4π2R2π[θ+2π−θ]=R(2π−θ)θ4π2
|
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - Assertion- Reason
14 Videos
- CURRENT ELECTRICITYBOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - Section D - Chapter End Test
29 Videos
- CURRENT ELECTRICITYBOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - Section - C
1 Videos
- ATOMIC PHYSICSBOOK - A2ZCHAPTER - ATOMIC PHYSICSEXERCISE - Section D - Chapter End Test
30 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
Knowledge Check
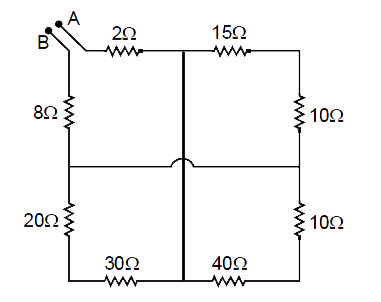
The equivalent resistance between points A and B is
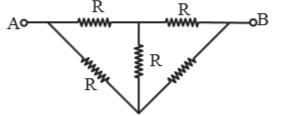 A2RB34RC43RDR
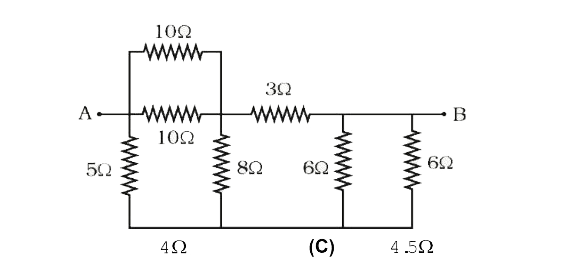
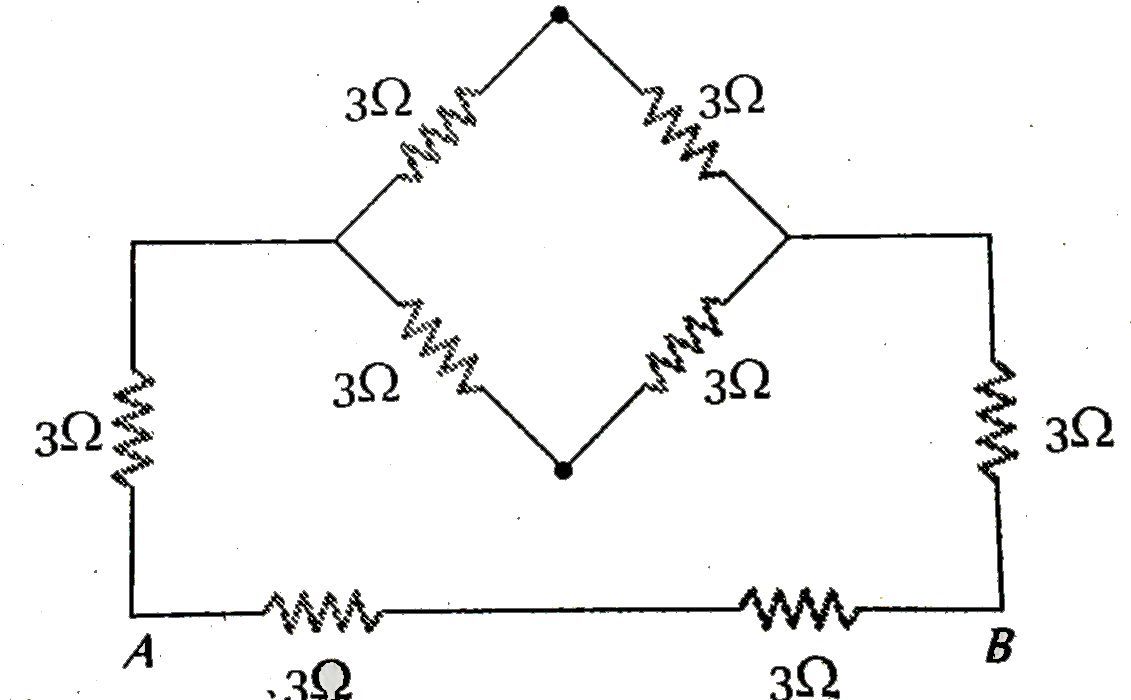
A2RB34RC43RDRThe equivalent resistance between points A and B is
 A32.5ΩB22.5ΩC12.5ΩD42.5Ω
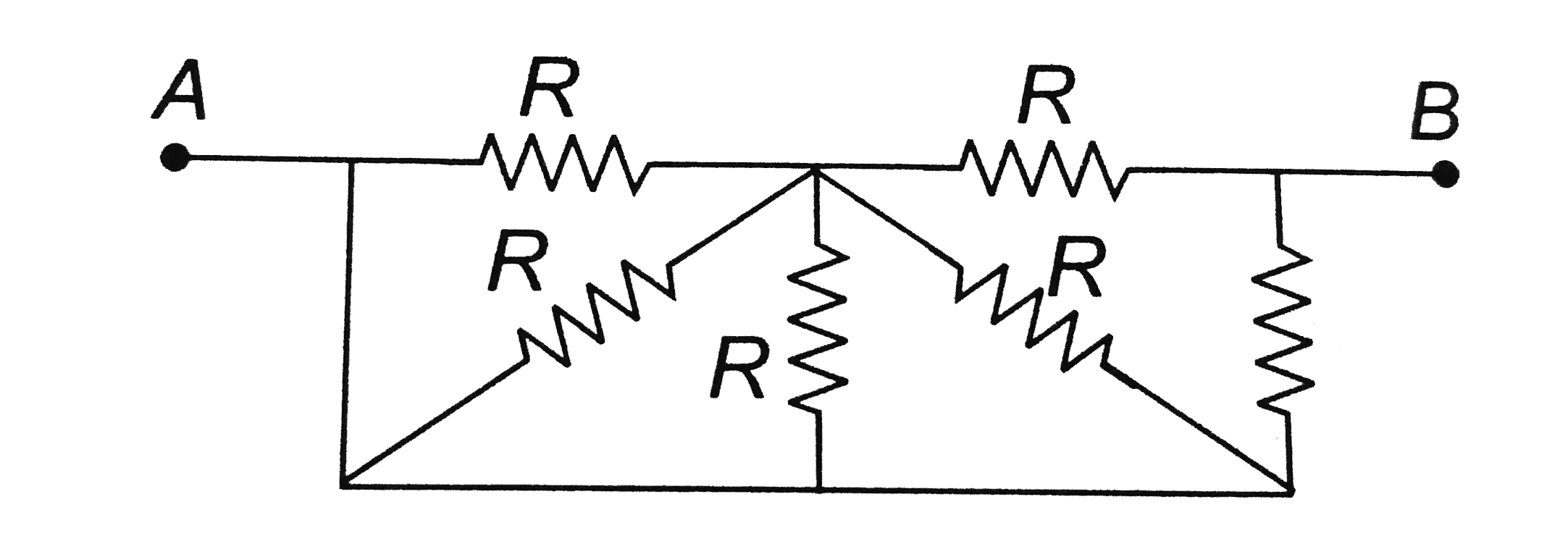
A32.5ΩB22.5ΩC12.5ΩD42.5ΩEquivalent resistance between A and B will be
 A2 ohmB18 ohmC6 ohmD3.6 ohm
A2 ohmB18 ohmC6 ohmD3.6 ohm
Find the equivalent resistance between point A and B
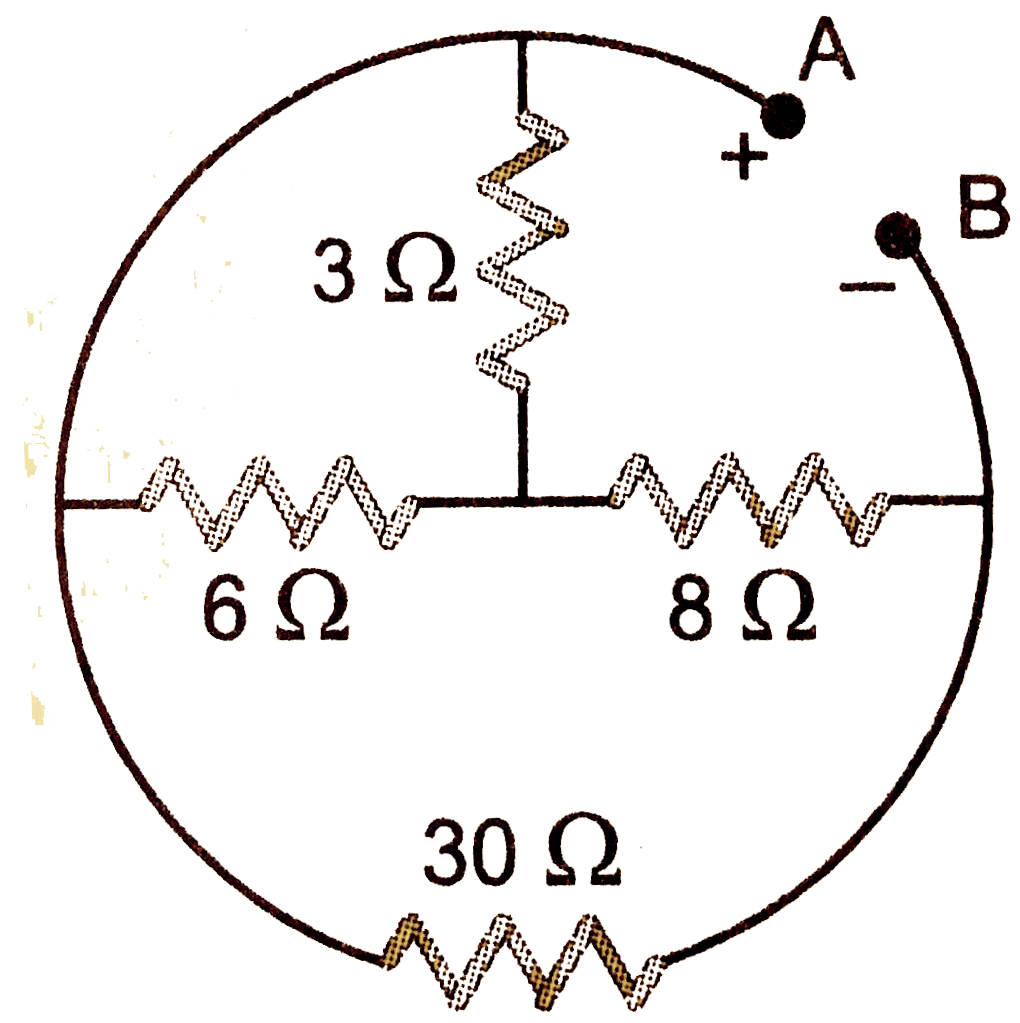
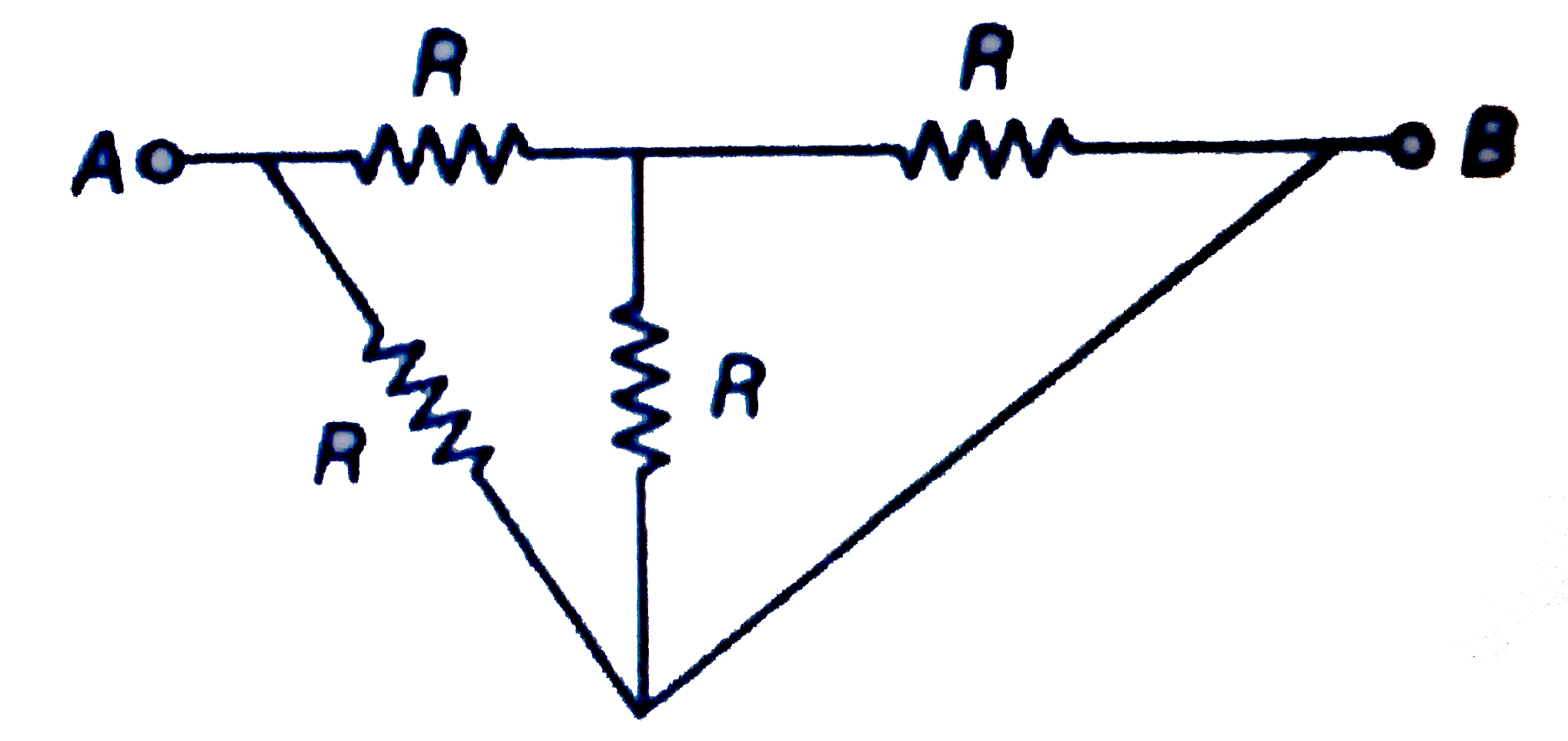
View SolutionThe equivalent resistance between points A and B
View SolutionThe equivalent resistance between points A and B

View SolutionThe equivalent resistance between the point A and B is
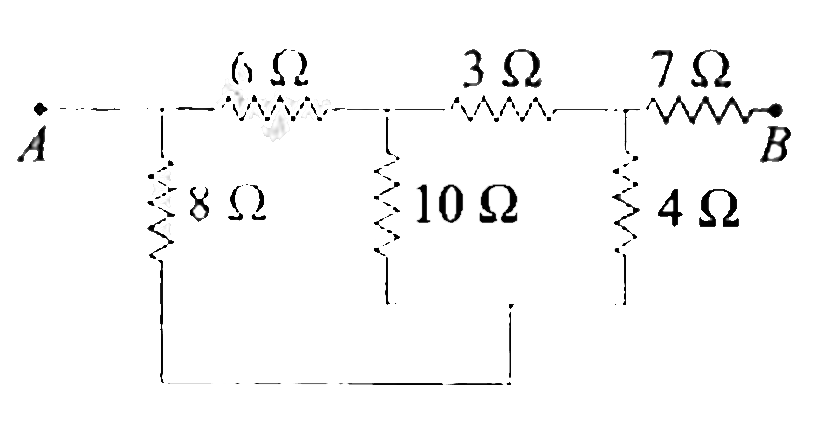
View SolutionThe equivalent resistance between the points A and B is:
View Solution