In three line segments OA OB and OC points L M N respectively are so chosen that LM || AB and MN || BC but neither of L M N nor of A B C are collinear. Show that LN ||AC.
We have LM || AB and MN || BCTherefore by basic proportionality theorem We have Thus LN divides sides OA and OC of ΔOAC in the same ratio. Therefore by the converse of basic proportionality theorem we have LN || AC
Related Solutions
In three line segments point respectively are so chosen that but neither of nor of are collinear. Show that .
View SolutionIn three line segments point respectively are so chosen that but neither of nor of are collinear. Show that
View Solutionযদি বাস্তব সংখ্যা এবং হয়, তবে দেখাও যে
View SolutionIf the area of the rhombus enclosed by the lines is 2 sq. units, then, a) l,m,n are in G.P b) l,n,m are in G.P. c) lm=n d) ln=m
View SolutionIf the area of the rhombus enclosed by the lines is 2 sq. units, then, a) l,m,n are in G.P b) l,n,m are in G.P. c) lm=n d) ln=m
View SolutionIf the area of the rhombus enclosed by the lines is 2 sq. units, then, a) l,m,n are in G.P b) l,n,m are in G.P. c) lm=n d) ln=m
View SolutionIf l,m and n are real numbers such that ,
then show that
View Solution
View SolutionFind the value of .
View SolutionIf I, m and n are real numbers such that l^2 + m^2 + n^2 = 0 , then show that [[1+l^2,lm,ln],[lm,1+m^2,mn],[ln,mn,1+n^2]]=1
View SolutionABC एक समबाहु त्रिभुज है जिसकी भुजा AB, BC,CA का मध्यबिन्दु क्रमशः L,M,N हैं। यदि LN,LM,MN का मध्यबिन्दु क्रमशः X,Y, Zहो, और यदि AB=16 सेमी हो, तो XY का ‘मान कौन-सा होगा?
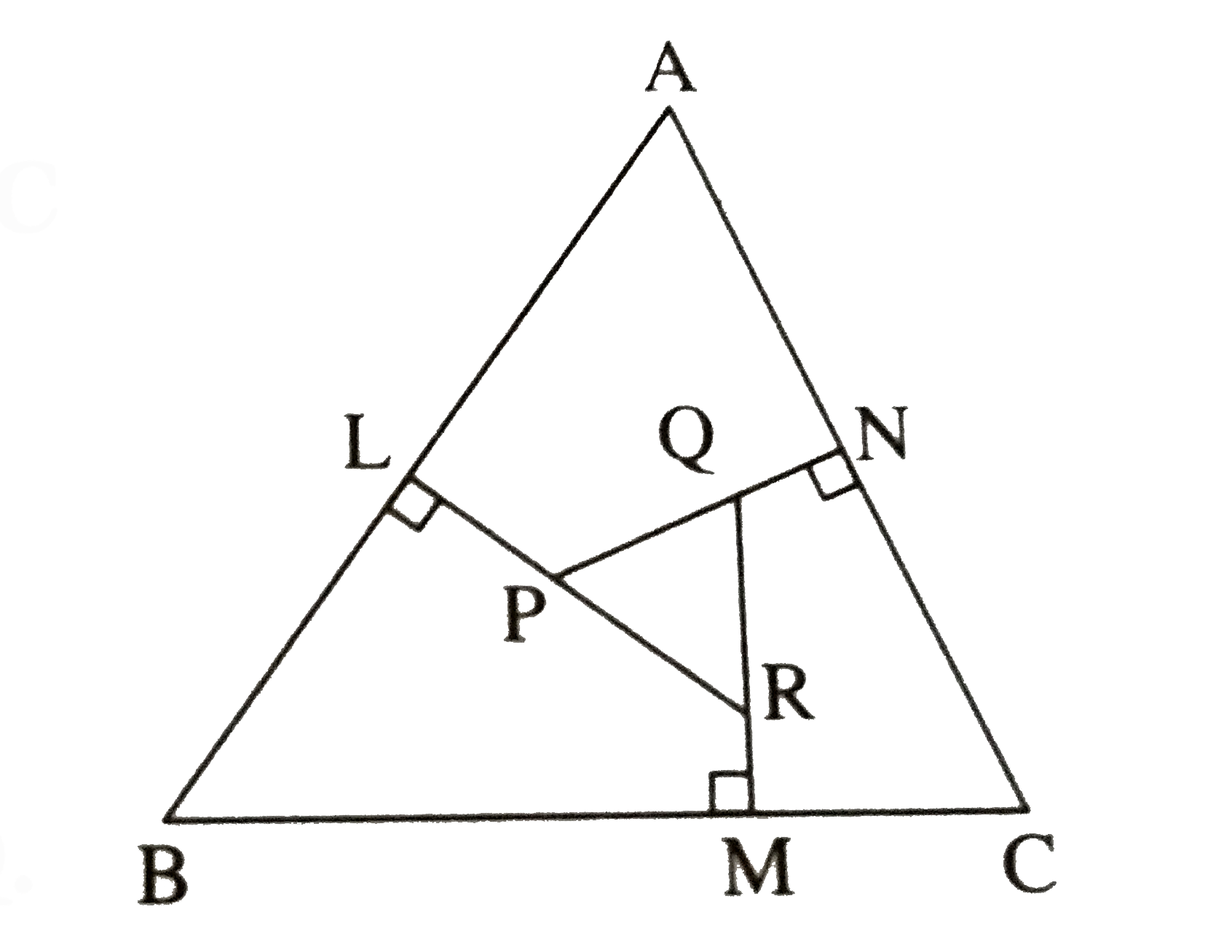
View SolutionIn are points on side AB,BC,AC respectively.
Perpendiculars drawn at L,M,N form .
Prove that .
View SolutionIn triangle ABC, if L and M are points on the sides AB and AC respectively, LM||BC is. Prove that ar (LOB) = ar (MOC).
View SolutionIn triangleABC , it L and M are points on AB and AC respectively such that LM||BC. Prove that : ar(triangleLCM) = ar(triangleLBM)
View SolutionIn triangleABC , it L and M are points on AB and AC respectively such that LM||BC. Prove that : ar(triangleLBC) = ar(triangleMBC)
View SolutionIn , if L and M are the points on AB and AC, respectively such that . Prove that .
View SolutionIn , if L and M are the points on AB and AC, respectively such that . Prove that .
View SolutionIf are three lines such that and prove that
View SolutionIf triangleABC There is a point on the inflection of K, and perpendiculars PL, PM and PN are placed on the line segments BC, CA and AB respectively. Show that the points L, M and N are collinear
View SolutionIf then the value of wll be
View Solution