A sphere of mass M and Radius R2 has a concentric cavity of Radius R1 as shown in figure. The force F exerted by the sphere on a particle of mass m located at a distance r from the centre of sphere varies as O ≤ r ≤ ∞
Correct option: BExplanation:when0 ≤ r ≤ R1 F = 0 as inside cavity intensity is zerowhen R1 ≤ r ≤ R2 F ∝ Rwhen r > R2 F ∝ 1/R
Related Solutions
A solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass m is
View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distanace R/4 from the centre of sphere. The gravitational force on mass m is
View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distanace R/4 from the centre of sphere. The gravitational force on mass m is
View SolutionA sphere of mass m and radius has a concentric cavity of radius , The force exerted by the sphere on a particle of unit mass located at a distance r from the centre varies as
View SolutionA sphare of mass M and has a concentric cavity of radius as shown in figure The force F exerted by the sphere on a particle of mass m located at a distance r from the centre of sphere veries as .
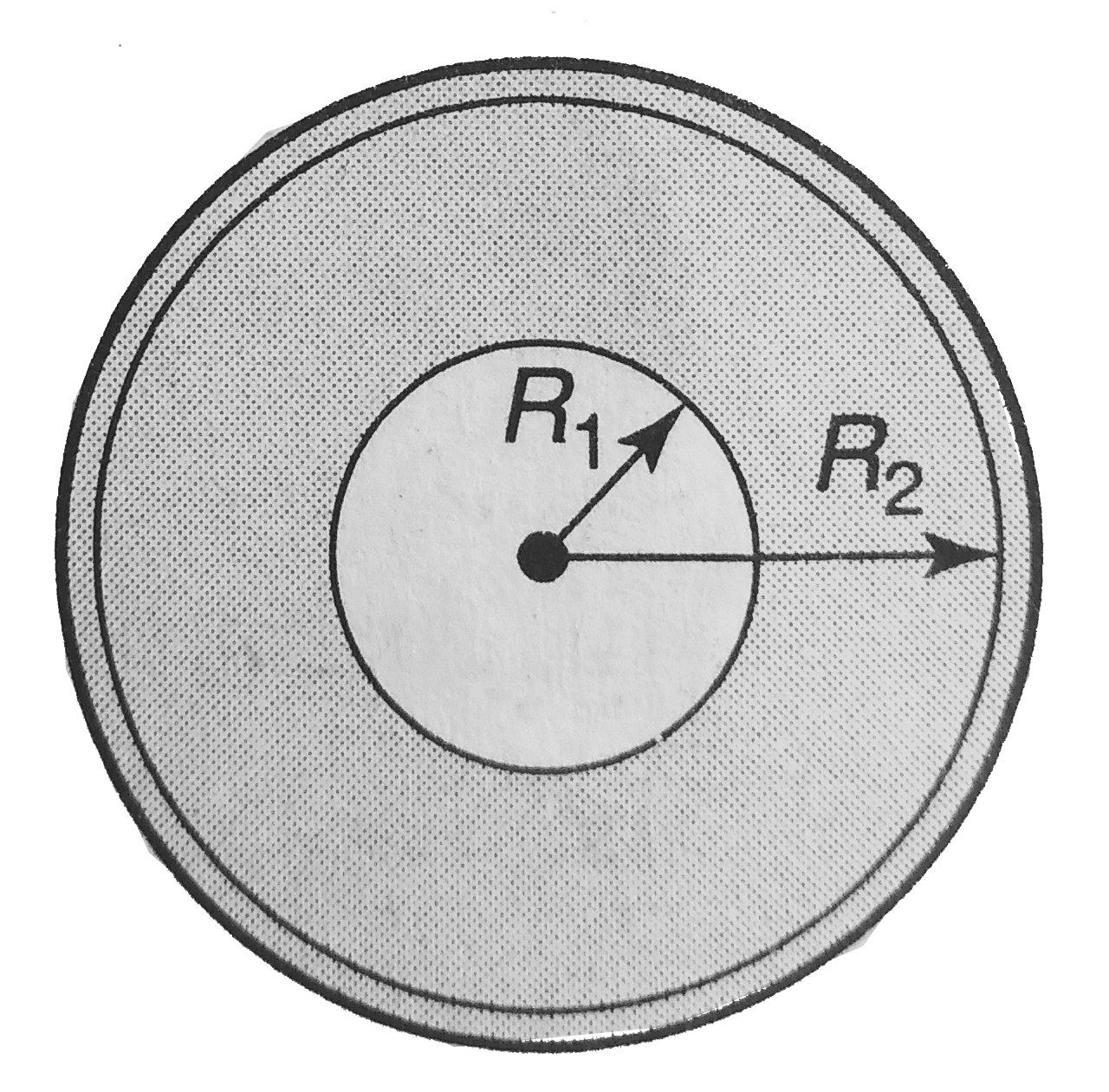
View SolutionA sphere of mass M and has a concentric cavity of radius as shown in figure The force F exerted by the sphere on a particle of mass m located at a distance r from the centre of sphere veries as .

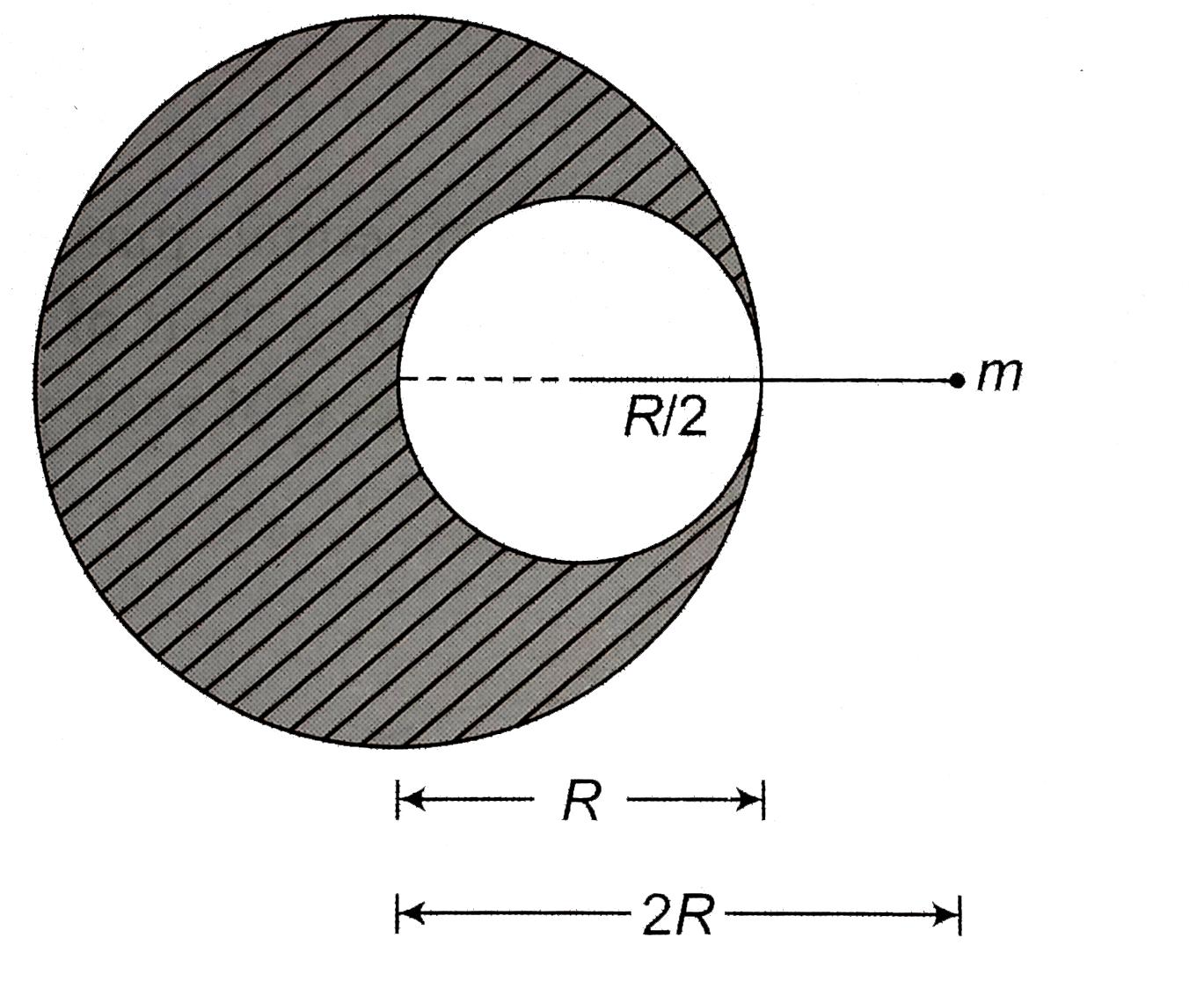
View SolutionA uniform sphere of mass M and radius R exerts a force F on a small mass m situated at a distance of 2R from the centre O of the sphere. A spherical portion of diameter R is cut from the sphere as shown in Fig. The force of attraction between the remaining part of the sphere and the mass m will be
View SolutionA cavity of radius R//2 is made inside a solid sphere of radius R . The centre of the cavity is located at a distance R//2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R//2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM//R^(2) , where M is the mass of the solide sphere]
View SolutionA cavity of radius R//2 is made inside a solid sphere of radius R . The centre of the cavity is located at a distance R//2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R//2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM//R^(2) , where M is the mass of the solide sphere]
View SolutionA cavity of radius is made inside a solid sphere of radius . The centre of the cavity is located at a distance from the centre of the sphere. The gravitational force on a particle of a mass at a distance from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here , where is the mass of the solid sphere]
View SolutionA cavity of radius is made inside a solid sphere of radius . The centre of the cavity is located at a distance from the centre of the sphere. The gravitational force on a particle of a mass at a distance from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here , where is the mass of the solide sphere]
View Solutionद्रव्यमान M और त्रिज्या R के एक ठोस गोले में, त्रिज्या की एक गोलीय गुहिका इस प्रकार बनाई गई है कि गुहिका का केंद्र गोले के केंद्र से से दूरी पर है। एक बिंदु द्रव्यमान m को गोले के केंद्र से की दूरी पर गुहिका के अंदर रखा जाता है। गोले और बिंदु द्रव्यमान m के बीच गुरुत्वाकर्षण खिंचाव है
View SolutionA particle of mass m is located outside a uniform sphere of mass M at a distance r from its centre. Find: (a) the potential energy of gravitational interaction of the particle and the sphere, (b) the gravitational force which the sphere exerts on the particle.
View SolutionInside a uniform sphere of mass M and radius R, a cavity of radius , is made in the sphere as shown :
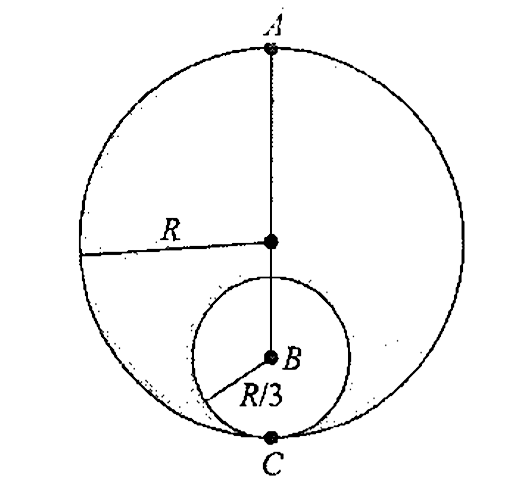
View SolutionFrom a solid sphere of mass and radius , a solid sphere of radius is removed as shown. Find gravitational force on mass as shown
View SolutionA particle of mass m is placed at a distance of 4R from the centre of a huge uniform sphere of mass M and radius R . A spherical cavity of diameter R is made in the sphere as shown in the figure. If the gravitational interaction potential energy of the system of mass m and the remaining sphere after making the cavity is (lambdaGMm)/(28R) . Find the value of lambda
View SolutionA particle of mass m is placed at a distance of 4R from the centre of a huge uniform sphere of mass M and radius R . A spherical cavity of diameter R is made in the sphere as shown in the figure. If the gravitational interaction potential energy of the system of mass m and the remaining sphere after making the cavity is (lambdaGMm)/(28R) . Find the value of lambda
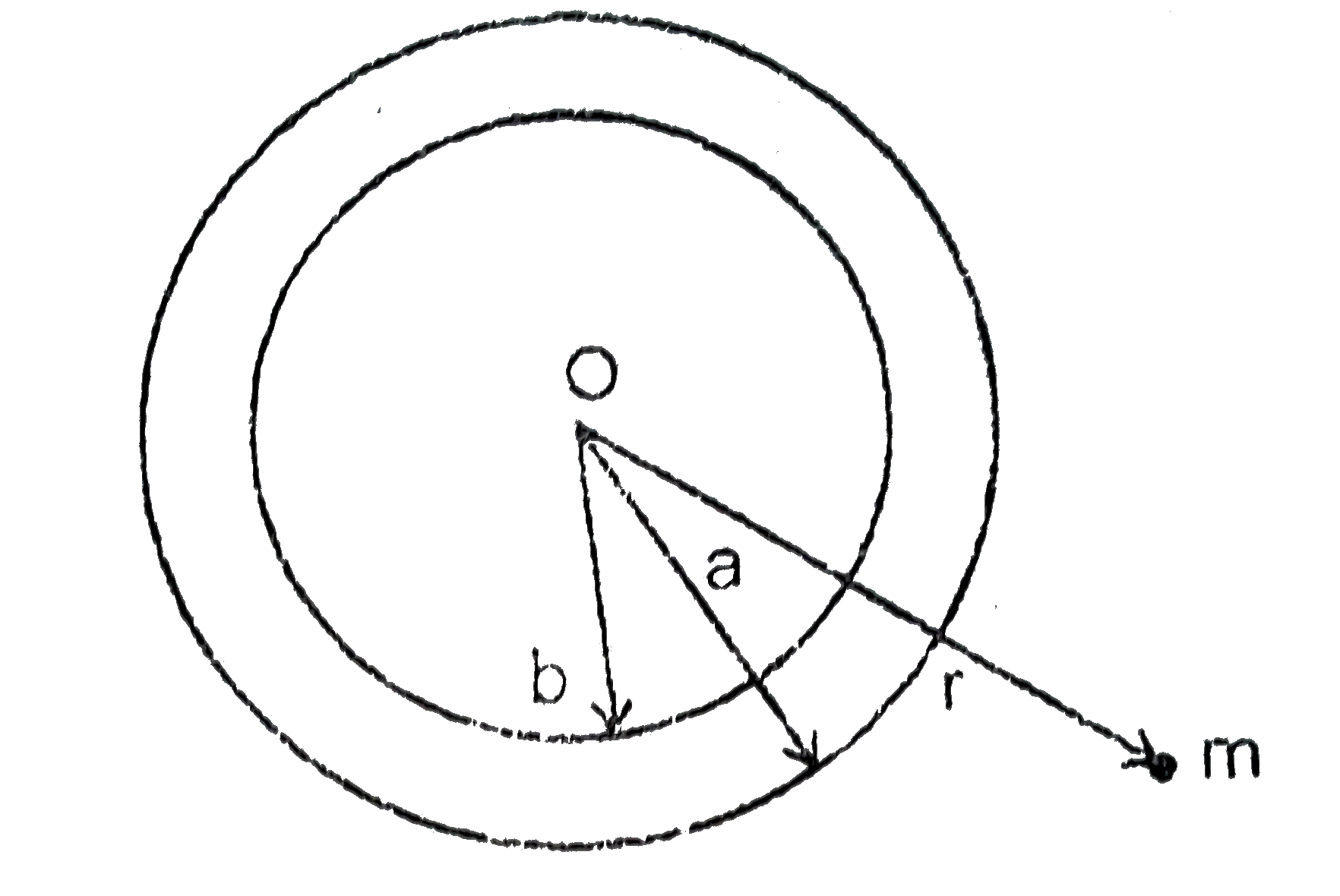
View SolutionA sphere of density and radius a has a concentric of radius b as shown in the
(a) Sketch the gravitational force exerted by the spehre on the particle of mass m located at a distance r from the centre of the sphere as a function of r in the range
(b) Sketch the corresponding curve for the potential energy u (r) of the system
 ,
,
View SolutionA sphere of density rho and radius a has a concentric of radius b as shown in the (a) Sketch the gravitational force exerted by the spehre on the particle of mass m located at a distance r from the centre of the sphere as a function of r in the range 0 le r le oo (b) Sketch the corresponding curve for the potential energy u (r) of the system ,
View SolutionA fixed sphere of radius R and uniform density rho has a spherical cavity of radius R//2 such that the surface of the cavity passes through the centre of the sphere. A particle of mass m is located at the centre (A) of the velocity. Calculated (a) The gravitational field at A . (b) The velocity with which the particle strikes the centre O of the sphere. (Neglect earth's gravity)
View Solution