After charging a capacitor C to a potential V it is connected across an ideal inductor L. The capacitor starts discharging simple harmonically at time t = 0. The charge on the capacitor at a later time instant is q and the periodic time of simple harmonic oscillations is T. Therefore a q = CV sin ωtb q = CV cos ωtc T = 2π√1/LCd T = 2π √LC
Correct option b dExplanation:
Related Solutions
A charged capacitor and an inductor are connected in series. At time t = 0, the current is zero, but the capacitor is charged. If T is the period of the resulting oscillations, the next time after t = 0, the maximum voltage across the inductor is
View SolutionA charge Q is given to the plates of an isolated capacitor of capacitance C. Now, the terminals of this capacitor are connected to the terminals of an inductor L at t = 0. After how much time will the energy stored in the capacitor and the Inductor become equal?
View SolutionA charge Q is given to the plates of an isolated capacitor of capacitance C. Now, the terminals of this capacitor are connected to the terminals of an inductor L at t = 0. After how much time will the energy stored in the capacitor and the Inductor become equal?
View Solutionधारिता C वाले संधारित्र को प्रतिरोध R के साथ वि. वा. ब. वाली बैटरी से आवेशित किया जाता है। यदि संधारित्र पर अधिकतम आवेश Q है तो समय t पर संधारित्र पर आवेश होगा :
View SolutionLet q be the charge on the capacitor at any time t. The voltage V across the capacitor is
View SolutionA capacitor is connected across an inductor. At time t = 0 charge on the capacitor is equal to 1/sqrt2q_"max" , where q_"max" is the maximum charge on the capacitor. The time t, at which the energy stored in the capacitor is equal to the energy stored in the inductor is (The inductance of the inductor is L and capacitance of the capacitor is C. Resistance of the circuit is zero)
View SolutionA capacitor is connected across an inductor. At time t = 0 charge on the capacitor is equal to 1/sqrt2q_"max" , where q_"max" is the maximum charge on the capacitor. The time t, at which the energy stored in the capacitor is equal to the energy stored in the inductor is (The inductance of the inductor is L and capacitance of the capacitor is C. Resistance of the circuit is zero)
View SolutionAn inductor and two capacitors are connected in the circuit as show in Fig Initially capacitor A has no charge and capacitor B has CV charge. Assume that the circuit has no resistance at all. At t = 0 , switch S is closed, then [given LC = (2)/(pi^(2) xx 10^(4)) S^(2) and Cv = 100 mC]
View SolutionAn inductor and two capacitors are connected in the circuit as show in Fig Initially capacitor A has no charge and capacitor B has CV charge. Assume that the circuit has no resistance at all. At t = 0 , switch S is closed, then [given LC = (2)/(pi^(2) xx 10^(4)) S^(2) and Cv = 100 mC]
View SolutionA capacitor is charged to 20 V. The charging battery is then disconnected , and a 15 mH coil is connected in series with the capacitor so that LC oscillations occur. Write the equation for variation of charge on capacitor and current in the inductor with time taking the instant at which inductor is connected to the capacitor as t=0.
View SolutionA 1.5 mu F capacitor is charged to 20 V. The charging battery is then disconnected , and a 15 mH coil is connected in series with the capacitor so that LC oscillations occur. Write the equation for variation of charge on capacitor and current in the inductor with time taking the instant at which inductor is connected to the capacitor as t=0.
View SolutionDuring charging a capacitor variation of potential V of the capacitor with time t is shown as
View Solutionकिसी आवेशित संधारित्र को एक प्रेरित्र के साथ जोड़कर अनावेशन क्रिया (discharging process) के क्रम में विद्युतीय दोलन होता हैं । इस प्रक्रम में संधारित्र की विद्युत - ऊर्जा एंव प्रेरित्र की चुंबकीय ऊर्जा के बीच परस्पर विनिमय (exchange) होता हैं । दोलन का एक चक्र पूरा होने में लगा समय , अर्थात आवर्तकाल T का मान L तथा C पर निर्भर करता हैं जिसके लिए संबंध मान्य होता हैं । चित्र में आवेशित संधारित्र के लिए विभवातंर है तथा स्विच S को समय t = 0 पर बंद किया जाता हैं |
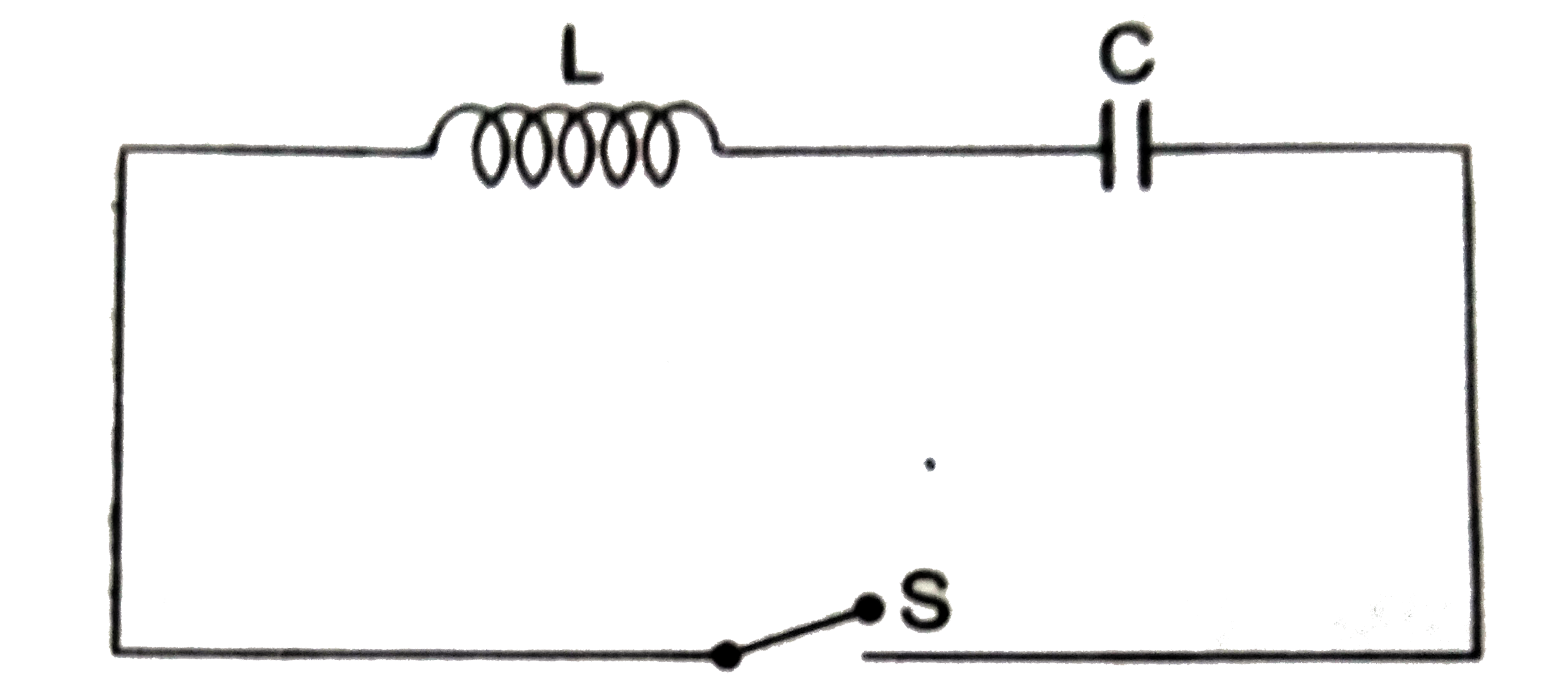
स्विच S को बंद करने के बाद संधारित्र पर सर्वप्रथम विभवांतर शून्य होने का समय हैं
View SolutionA capacitor of capacitance as C is given a charge Q. At ,it is connected to an ideal battery of emf through a resistance R. Find the charge on the capacitor at time t.
View SolutionA capacitor of capacitance as C is given a charge Q. At ,it is connected to an ideal battery of emf through a resistance R. Find the charge on the capacitor at time t.
View SolutionA capacitor of capacitance as C is given a charge Q. At ,it is connected to an ideal battery of emf through a resistance R. Find the charge on the capacitor at time t.
View SolutionA capacitor of capacitance as C is given a charge Q. At ,it is connected to an ideal battery of emf through a resistance R. Find the charge on the capacitor at time t.
View SolutionA charged capacitor is connected to an inductor at an instant of time t=0.If the capacitor and the inductor are taken to be pure, write down the equation of effective potential difference across the combination at any instant of time t and solve it for instantaneous current through I the combination.Explain brefly the exchange of electric and magnetic energy between the capacitor and the inductor.
View SolutionA charged capacitor is connected to an inductor at an instant of time t = 0. If the capacitor and the inductor are taken to be pure, wirte down the equation of effective potential difference across the combination at any instant of time t and solve if for instantaneous current through the combination. Explain briefly the exchange of electric and magnetic energy between the capacitor and the inductor.
View SolutionA charged capacitro and an inductor are connected in series. At time t = 0 , the current is zero but the capacitor is charged, If T is the period of resulting oscillations, then the time after which current in the circuit becomes maximum , is
View Solution