A charge Q is given to the plates of an isolated capacitor of capacitance C. Now, the terminals of this capacitor are connected to the terminals of an inductor L at t = 0. After how much time will the energy stored in the capacitor and the Inductor become equal?
π√(LC)/2
π√(LC)/4
5π√(LC)/2
π√(LC)
The correct Answer is:B
To solve the problem, we need to determine the time at which the energy stored in the capacitor equals the energy stored in the inductor after they are connected in an LC circuit.
1. Initial Energy in the Capacitor:
The initial energy stored in the capacitor when it has charge Q and capacitance C is given by the formula:
UC=Q22C
2. Energy in the Inductor:
The energy stored in the inductor with current I is given by:
UL=12LI2
3. Condition for Equal Energy:
We need to find the time t when the energy in the capacitor equals the energy in the inductor:
UC=UL
Substituting the expressions for UC and UL:
Q22C=12LI2
4. Expressing Current in Terms of Charge:
In an LC circuit, the charge q(t) on the capacitor at time t can be expressed as:
q(t)=Qcos(ωt)
where ω=1√LC.
The current I can be expressed as the rate of change of charge:
I=−dqdt=−ddt(Qcos(ωt))=Qωsin(ωt)
5. Substituting Current into Energy Equation:
Substitute I into the energy equation:
Q22C=12L(Qωsin(ωt))2
Simplifying this gives:
Q22C=12LQ2ω2sin2(ωt)
6. Cancelling Q22:
Since Q2 is common on both sides, we can cancel it (assuming Q≠0):
1C=Lω2sin2(ωt)
7. Substituting ω:
Recall that ω=1√LC:
1C=L(1√LC)2sin2(ωt)
This simplifies to:
1C=LLCsin2(ωt)
1=sin2(ωt)
8. Finding the Time:
The equation sin2(ωt)=12 implies:
sin(ωt)=1√2
This occurs at:
ωt=π4+nπ(n∈Z)
For the first positive solution:
t=π4ω=π4√LC
Final Answer:
Thus, the time at which the energy stored in the capacitor and the inductor becomes equal is:
t=π4√LC
The initial energy stored in the capacitor when it has charge Q and capacitance C is given by the formula:
UC=Q22C
The energy stored in the inductor with current I is given by:
UL=12LI2
We need to find the time t when the energy in the capacitor equals the energy in the inductor:
UC=UL
Substituting the expressions for UC and UL:
Q22C=12LI2
In an LC circuit, the charge q(t) on the capacitor at time t can be expressed as:
q(t)=Qcos(ωt)
where ω=1√LC.
I=−dqdt=−ddt(Qcos(ωt))=Qωsin(ωt)
Substitute I into the energy equation:
Q22C=12L(Qωsin(ωt))2
Simplifying this gives:
Q22C=12LQ2ω2sin2(ωt)
Since Q2 is common on both sides, we can cancel it (assuming Q≠0):
1C=Lω2sin2(ωt)
Recall that ω=1√LC:
1C=L(1√LC)2sin2(ωt)
This simplifies to:
1C=LLCsin2(ωt)
1=sin2(ωt)
The equation sin2(ωt)=12 implies:
sin(ωt)=1√2
This occurs at:
ωt=π4+nπ(n∈Z)
For the first positive solution:
t=π4ω=π4√LC
Thus, the time at which the energy stored in the capacitor and the inductor becomes equal is:
t=π4√LC
Topper's Solved these Questions
- PHYSICS PART2Book:FIITJEEChapter:PHYSICS PART2Exercise:Section (I) : Subjective
Explore 4 Videos
- PHYSICS PART2Book:FIITJEEChapter:PHYSICS PART2Exercise:Section (II) : MCQ
Explore 27 Videos
- PHYSICS PART-IIIBook:FIITJEEChapter:PHYSICS PART-IIIExercise:NUMERICAL BASED QUESTIONS DECIMAL TYPE
Explore 11 Videos
- ROTATIONAL MECHANICSBook:FIITJEEChapter:ROTATIONAL MECHANICSExercise:COMPREHENSION - IV
Explore 2 Videos
Similar Questions
Each plate of a parallel plate capacitor has a charge q on it. The capacitor is now connected to a battery. Now,
View SolutionA capacitor of capacitance 54μF is charged ot a potential of 25 V and then connected to a 15 mH inductor to produce oscillations. What was the energy stored in the capacitor initially and to what wavelength will the circuit respond ?
View Solution
Knowledge Check
In the given at t=0, switch S is closed.
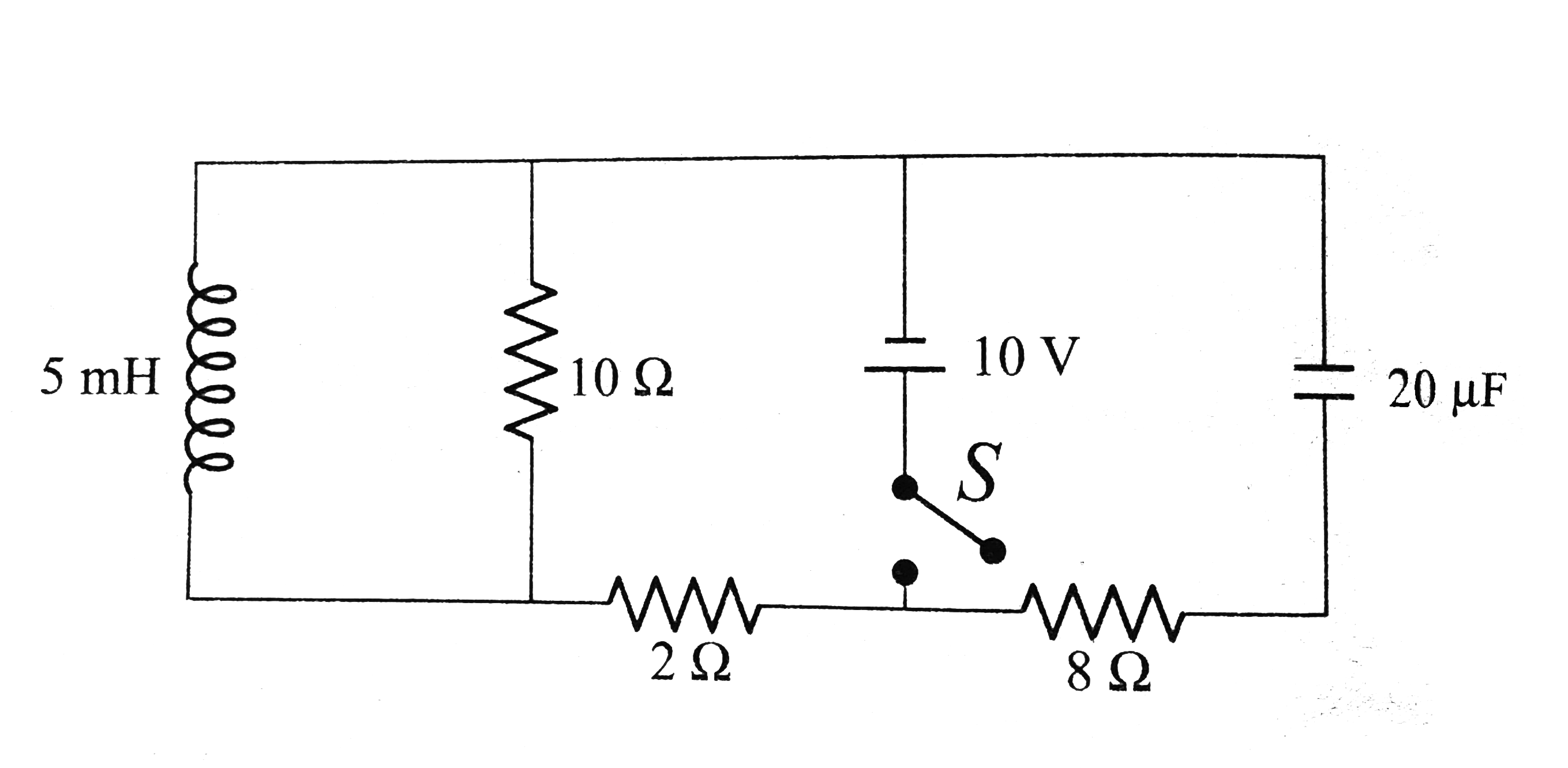
The energy stored in the capacitor and inductor, respectively, at t→∞ will beA1mJ and 62.5mJB62.5mJ and 1mJC2mJ and 62.5mJD1mJ and 60mJConsider a parallel plate capacitor originally with a charge q0 capacitance C0 and potential difference ΔV0 There is an electrostatic force of magnitude F0 between the plates and the capacitor has a stored energy U0. The terminals of the capacitor are connected to another capacitor of same capacitance and charge.
What is the direction of the electrostatic force on the dielectric slab while it is being increased?AThe force pulls the slab into the capacitorBThe force pushes the slab out of the capacitorCThere is no electrostatic force of the slabDCan't be saidIf there are n capacitors each of capacitance C in series combination connected to a V volt source, then the energy stored in each capacitor is equal to :
AnCV2B12nCV2CCV22nDCV22n2
A capacitor of capacitance C1 is charged to a potential V1 , while another capacitor of capacitance C2 is charged to a potential difference V2 . The capacitors are now disconnected from their respective charging batteries and connected in parallel to each other
Find the total energy stored in the two capacitors before they are connected .
View SolutionA fully charged capacitor C with initial charge q0 is connected to a coil of self inductance L at t=0. The time at which the energy is stored equally between the electric and the magnetic fields is
View SolutionA battery of 20V is connected to a capacitor of capacitance 10μF. Now battery is removed and this capacitor is connected to a second uncharged capacitor. If the charge distributes equally on these two capacitors, the total energy stored in the two capacitors will be
View SolutionConsider a parallel plate capacitor originally with a charge q0 capacitance C0 and potential difference ΔV0 There is an electrostatic force of magnitude F0 between the plates and the capacitor has a stored energy U0. The terminals of the capacitor are connected to another capacitor of same capacitance and charge.
A dielectric slab with ke>1 is inserted between the plates of the first capacitor . Which quantity decreases?
View SolutionIn the circuit shown, left plate of the capacitor with capacitance C is given a charge Q0 and plates of capacitor are connected across the battery as shown. Amount of charge that will flow from battery to left plate of capacitor when key is closed is:
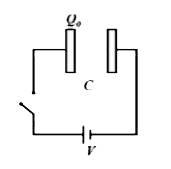
View Solution