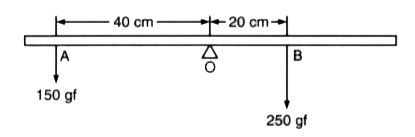
Figure shows a uniform metre rule weighing 100gf pivoted at its centre ‘O’. Two weights of 150gf and 250gf hang from the metre rule as shown. Calculate : a Total C.W. moment about ‘O’. b TotalA.C.W. moment about ‘O’. c Differentiate of C.W. andA.C.W. moments. d The distance from ‘O’ where a 100gf weight should be suspended to balance the metre scale.
at 60cm mark at D.
Related Solutions
The diagram in Fig.1.34 shows a uniform metre rule weighing 100gf, pivoted at its centre O. Two weights 150 gf and 250 gf hang from the points A and B respectively of the metre rule such that OA= 40cm and OB=20cm . Calculate (i) the total anticlockwise moment about O, (ii) the total clockwise moment about O, (iii) the difference of anticlockwise and clockwise moments, and (iv) the distance from O where a 100gf weight should be placed to balanced the metre rule.
View SolutionA uniform metre rule is pivoted as its mid point. A weight of 50gf is suspended at one end of it. Where should a weight of 100gf be suspended to keep the rule horizontal?
View SolutionA uniform metre rule is pivoted at its mid-point. A weight of 50 gf is suspended at one end. Where should be a weight of 100 gf suspended to keep the rule horizontal?
View SolutionA uniform half metre rule balances horizontally on a knife edge at 29 cm mark when a weight of 20 gf is suspended from one end. What is the weight of the half metre rule ?
View SolutionAn uniform metre scale of weight is balanced at mark, when a weight of is suspended at mark. Where must a weight be suspended to balance metre scale.
View SolutionFig.1.33 shows a uniform metre rule placed on a fulcrum at its mid point O and having a weight 40gf at the 10cm mark and a weight of 20gf at the 90cm mark. (i) Is the metre rule in equilibrium? If not , how will the turn?
(ii) How can the rule be brought in equilibrium by using an additional weight of 40 gf?
View SolutionA uniform metre rule of weight 10gf is pivoted at its 0 mark.
(i) What moment of force depresses the rule?
(ii) How can it can be made horizontal by applying a least force?
View SolutionA metre scale is supported on a wedge at its centre of gravity. A body of weight w is suspended from the 15 cm mark and another weight of 30 gram suspended from 71 cm mark balances it the metre scale remains perfectly horizontal. What is the weight of the body? Neglect the weight of the centre scale.
View SolutionDescribe a simple experiment to verify the principle of moments, if you are supplied with the metre rule, a fulcrum and two springs with slotted weights.
View SolutionCalculate the ratio of moment of inertia of a thin uniform disc about axis 1 and 2 marked in the figure. is the centre of the disc.

View SolutionMoment of inertial of a uniform symmetric plate as shown in figure about x-axis is l.. Moment of inertia centre of plate O and perpendicular to the plane of plate is
View SolutionMoment of inertial of a uniform symmetric plate as shown in figure about x-axis is l.. Moment of inertia centre of plate O and perpendicular to the plane of plate is
View Solutionचित्र 18.E2 में प्रदर्शित बस्तु पर O के परितः कुल बल-आघूर्ण की गणना करें
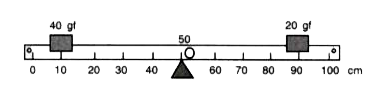
View SolutionA uniform meter scale balances at the 40 cm mark when weights of 10g and 20g are suspended from the 10cm and 20cm marks. The weight of the metre scale is
View Solutionbelow shows a uniform metre rule AB pivoted at its end A at the zero mark and supported at the other end B by a spring balance when a weight of 40kgf is suspended at its 40cm mark. This rule stays horizontal . Find the reading of the spring balance when the rule is of (i) negligible mass (ii) mass 20kg.
View SolutionThe diagram alongside shows a uniform metre rule of weight 100 gf being balanced on a knife edge placed at the 40 cm mark, by suspending a weight w gf at the mark 20 cm, find:
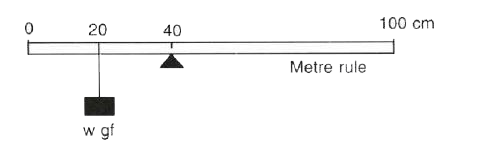
the resultant moment and its direction if the weight w is moved to the mark 30 cm.
View SolutionThe diagram in Fig.1.29 shows two forces F_1=5N and F_2=3N acting at points A and B of a rod pivoted at a point O, such that OA=2m and OB=4m Calculate: (i) the moment of force F_1 about O. (ii) the moment of force F_2 about O. (iii) total moment of the two forces about O.
View SolutionThe moment of a force of 10N about a fixed point O is 5 Nm. Calculate the distance of the point O from the line of action of the force.
View SolutionA uniform metre scale of weight 20 gf is supported on a wedge placed at 60 cm mark. If a weight of 30 gf is suspended at 15 cm mark, where should a weight 200 gf be suspended in order to balance the metre scale?
View SolutionA wheel of diameter 2m is shown in Fig 1.28 with axle at O. At force F= 2N is applied at B in the direction shown in figure, Calculate the moment of force about (i) the centre O, and (ii) the point A.
View Solution