AB is a diameter of a circle and. AC is its chord such that ∠BAC = 30o. If the tangent at C intersects AB extended at D then BC = BD.State true or false for each of the statement and justify your answer
Answer is.........
Related Solutions
AB is a diameter of a circle and AC is its chord such that . If the tengent at C intersects AB extended at D, then BC=BD.
View SolutionAB is a diameter of a circle and AC is its chord such that . If the tangent at C intersects AB extended at D, then BC=BD.
View SolutionAB is a diameter of a circle and AC is its chord such that . If the tengent at C intersects AB extended at D, then BC=BD.
View SolutionAB is the diameter and AC is a chord of a circle with centre O such that angle . The tangent to the circle at C intersects AB produced in D. Show that BC=BD.
View Solutionदिये गये चित्र में, AB वृत्त का व्यास तथा AC वृत्त की जीवा है तथा बिन्दु C पर स्पर्शी AB को बढ़ाने पर मिले बिन्दु D पर प्रतिच्छेद करती है। सिद्ध कीजिए कि BC = BD
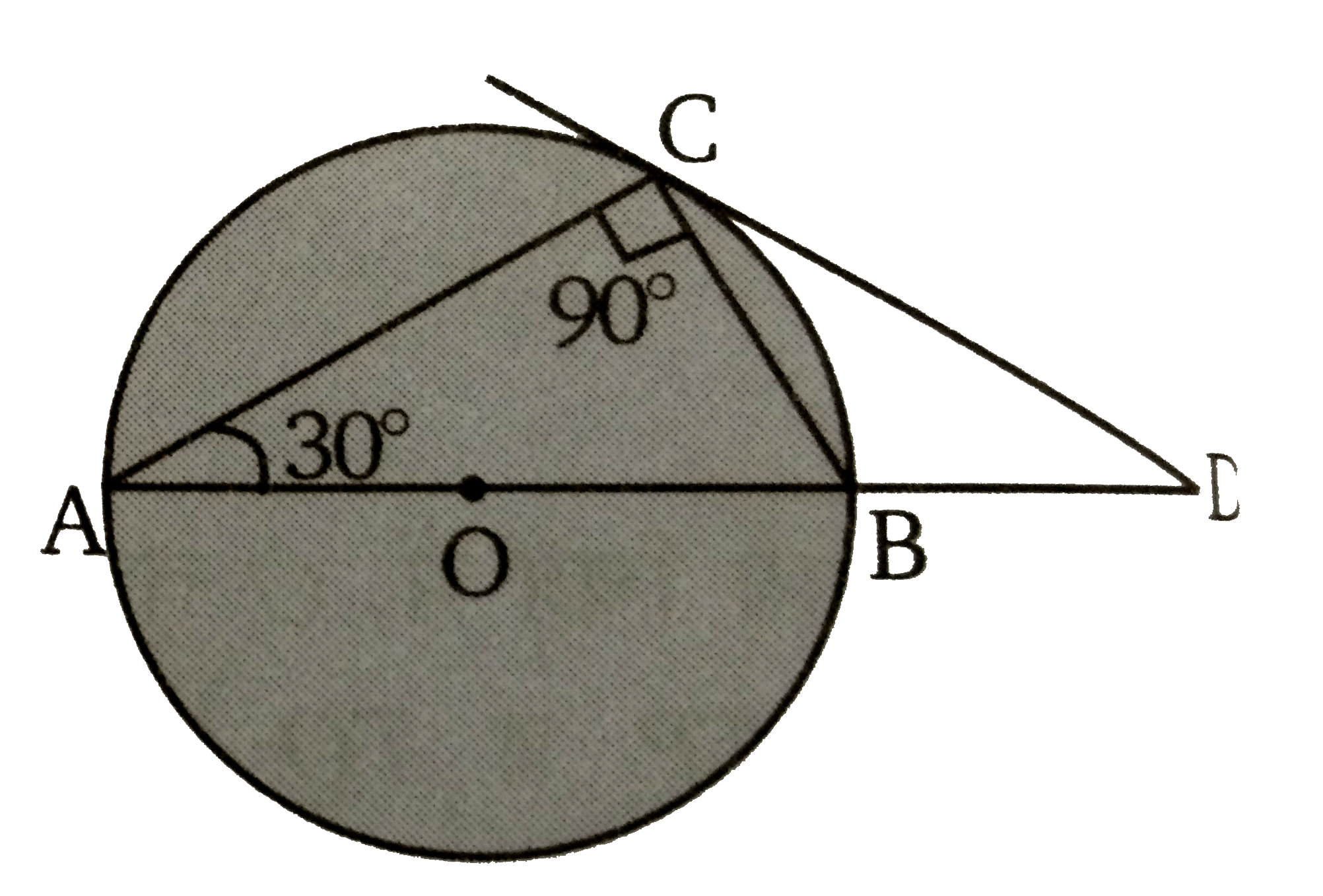
View SolutionAB is a diameter and AC is a chord of a circle with centre O such that . The tangent at C intersects AB at a point D. Prove that BC=BD.
View SolutionIn the given figure AB is the diameter and AC is the chord of a circle such that . The tangent at C intersects AB produced at D. Prove that :BC=BD.
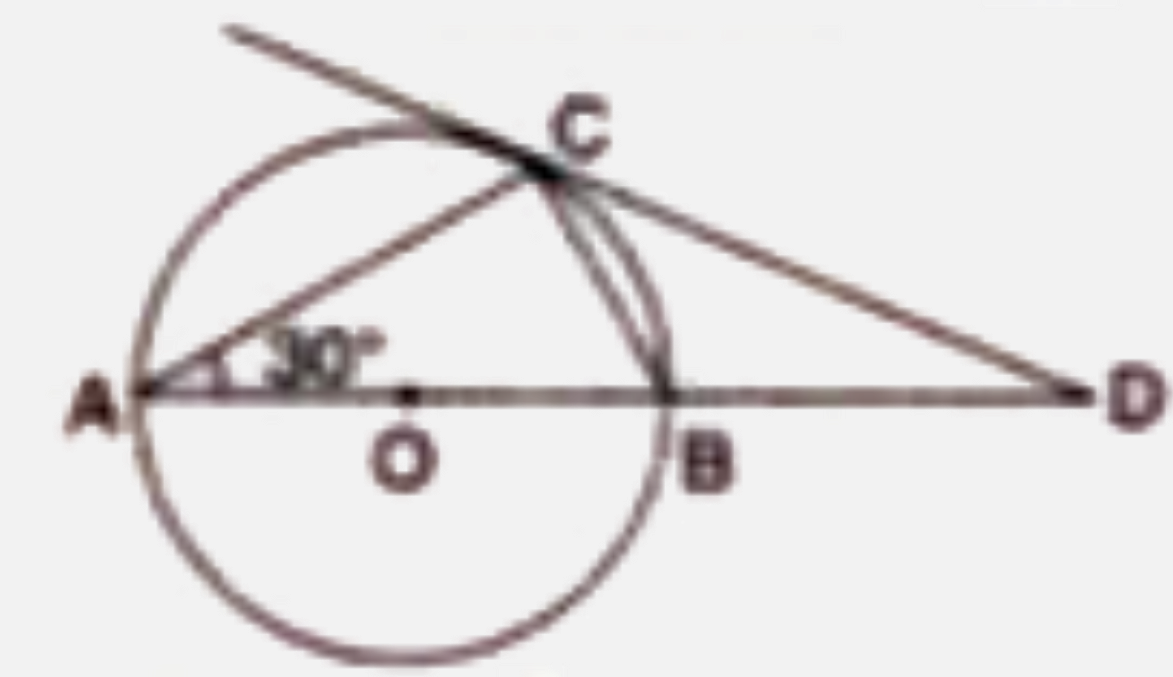
View SolutionWrite True/False for each and also give reason for your answer. In the figure, AB is the diameter of a circle and C is any point on the circle. AC^(2) + BC^(2) = AB^(2) Is.
View SolutionIn circle is drawn with diameter AB and it intersects BC at D. Prove that D is the midpoint of BC.
View SolutionAB एक वृत्त का व्यास है तथा इसकी जीवा BC, त्रिज्या के समान है। A तथा C से बनाई गई स्पर्शी एक-दूसरे से X पर मिलती हैं। है
View SolutionAB is a diameter and AC is a chord of the circle with centre at Q. the radius parallel to AC intersect the circle at D. Prove that D is the mid-point of the are BC.
View SolutionIn , AB=AC. If we draw a circle with diameter AB, the circle intersect BC at D, then BD:CD=?
View Solution(True/ False) If AOB is a diameter of a circle and C is a point on the circle, then .
View SolutionIf and are equal chord to circle with centre and is diameter then
View SolutionIf and are equal chord to circle with centre and is diameter then
View SolutionAB, AC of a circle intersect at the point D tangent to two chords, B and C. /_BCD=67^@ If, angleBAC How much?
View SolutionAB and AC are tangents to a circle with centre O. A is the external point of the circle. The line AO intersect the chord BC at D. The measure of the is
View SolutionSeg AB is a diameter of a circle with centre P. Seg AC is a chord. A secant through P and parallel to seg AC intersects the tangent drawn at C in D. Prove that line DB is a tangent to the circle.
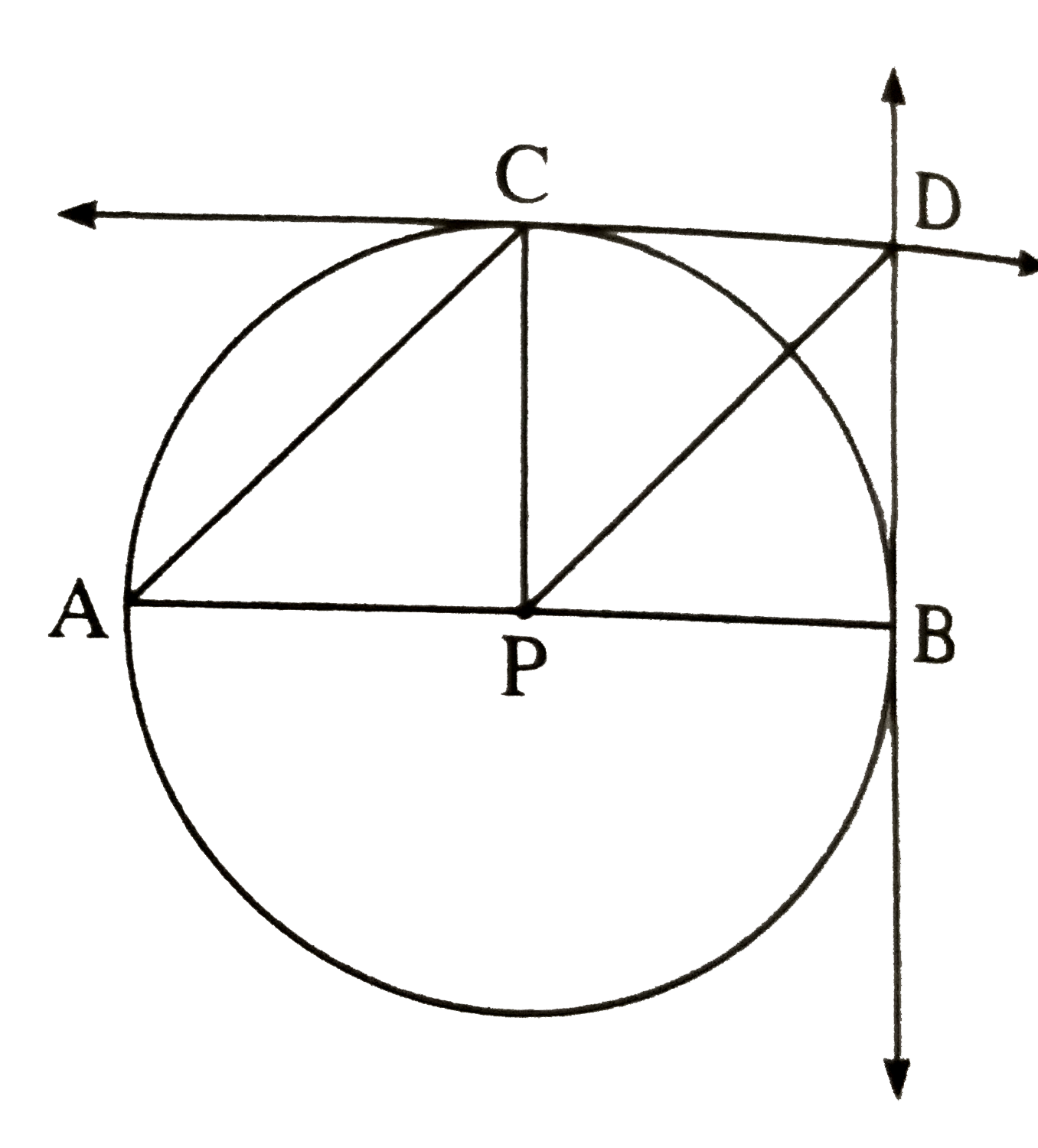
View SolutionAB is the diameter of a circle. C is a point on a tangent drawn to A. If AB = 8 cm. and AC = 6 cm. Then find the length of BC.
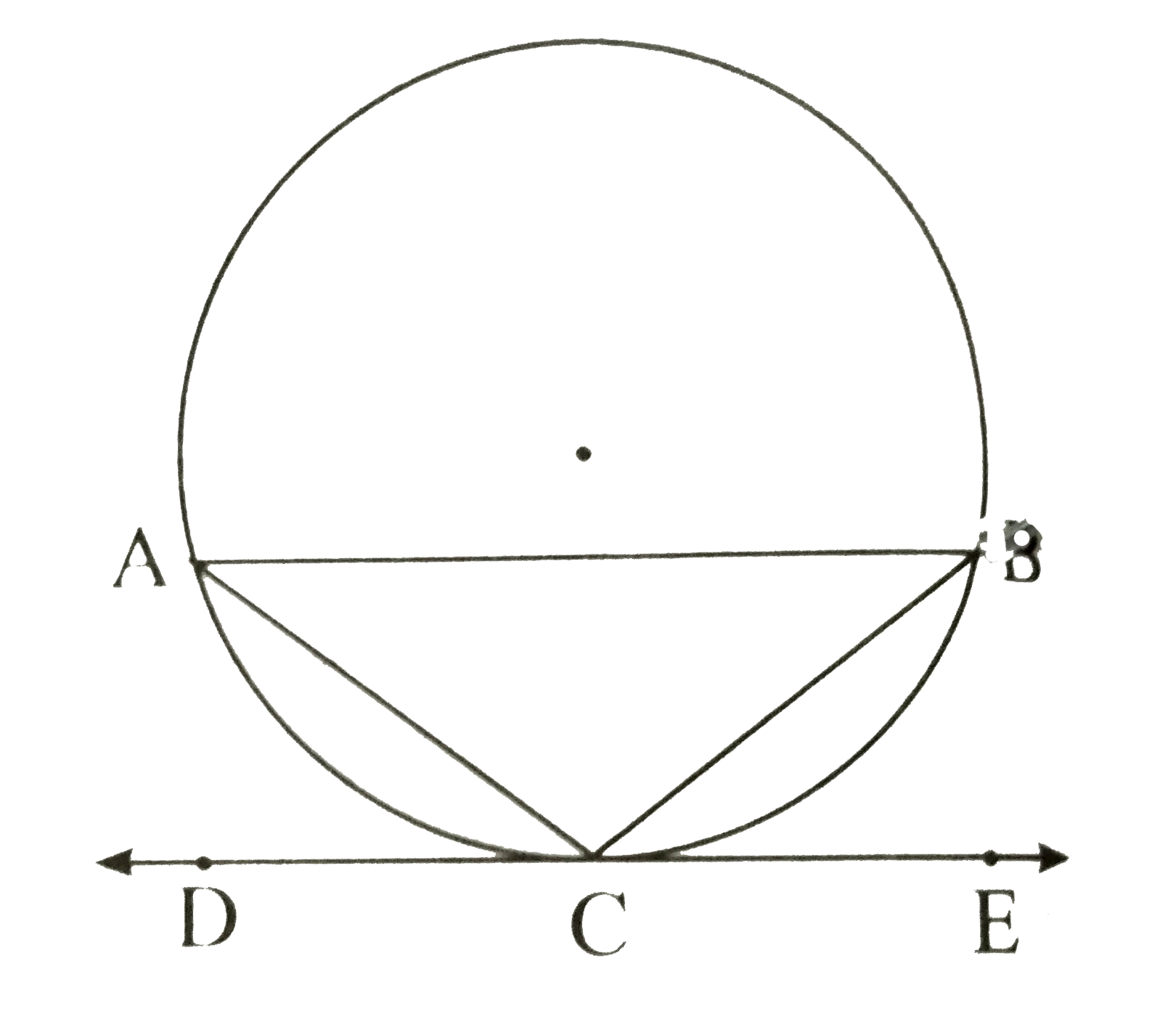
View SolutionIn the figure, chord tangent DE. Tangent DE touches the circle at point C then prove AC = BC.
View Solution