In the adjoining figure crescent is formed by two circles which touch at the point A. O is the centre of bigger circle. If CB = 9 cm and DE = 5 cm find the area of the shaded portion.
Let R and r be the radii of two circles. The 2R-r = 9. Join AD and CD Δ AOD - Δ DOC
Related Solutions
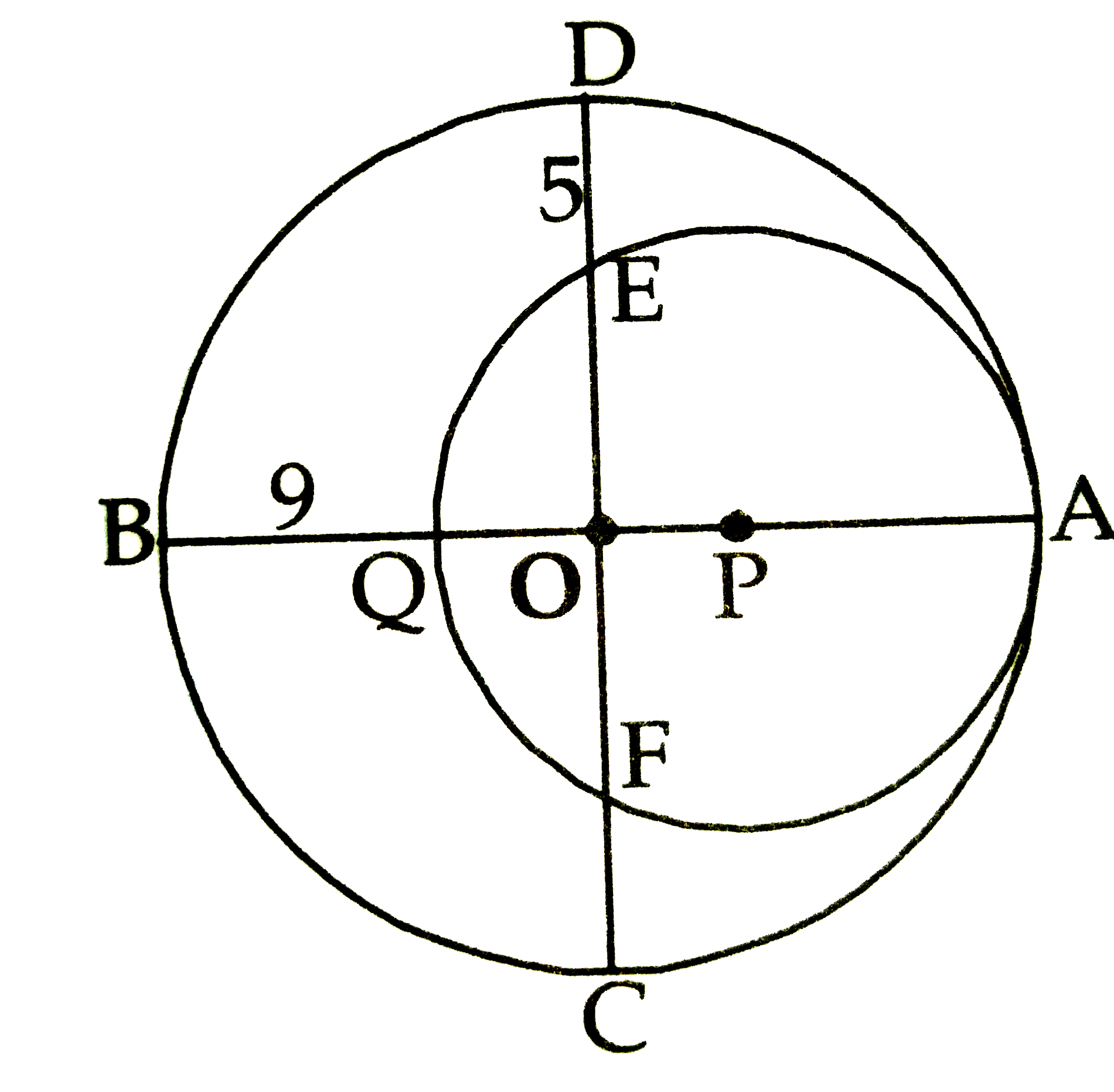
In the adjoining figure, two circles with centres O and P are touching internally at point A. If BQ = 9. DE = 5, then find the radii of the circles.

View SolutionIn the adjoining figure, CM = 5 cm, RB = 9 cm, , O is the centre of larger circle and K is the centre of smaller circle. Find the area of shaded region
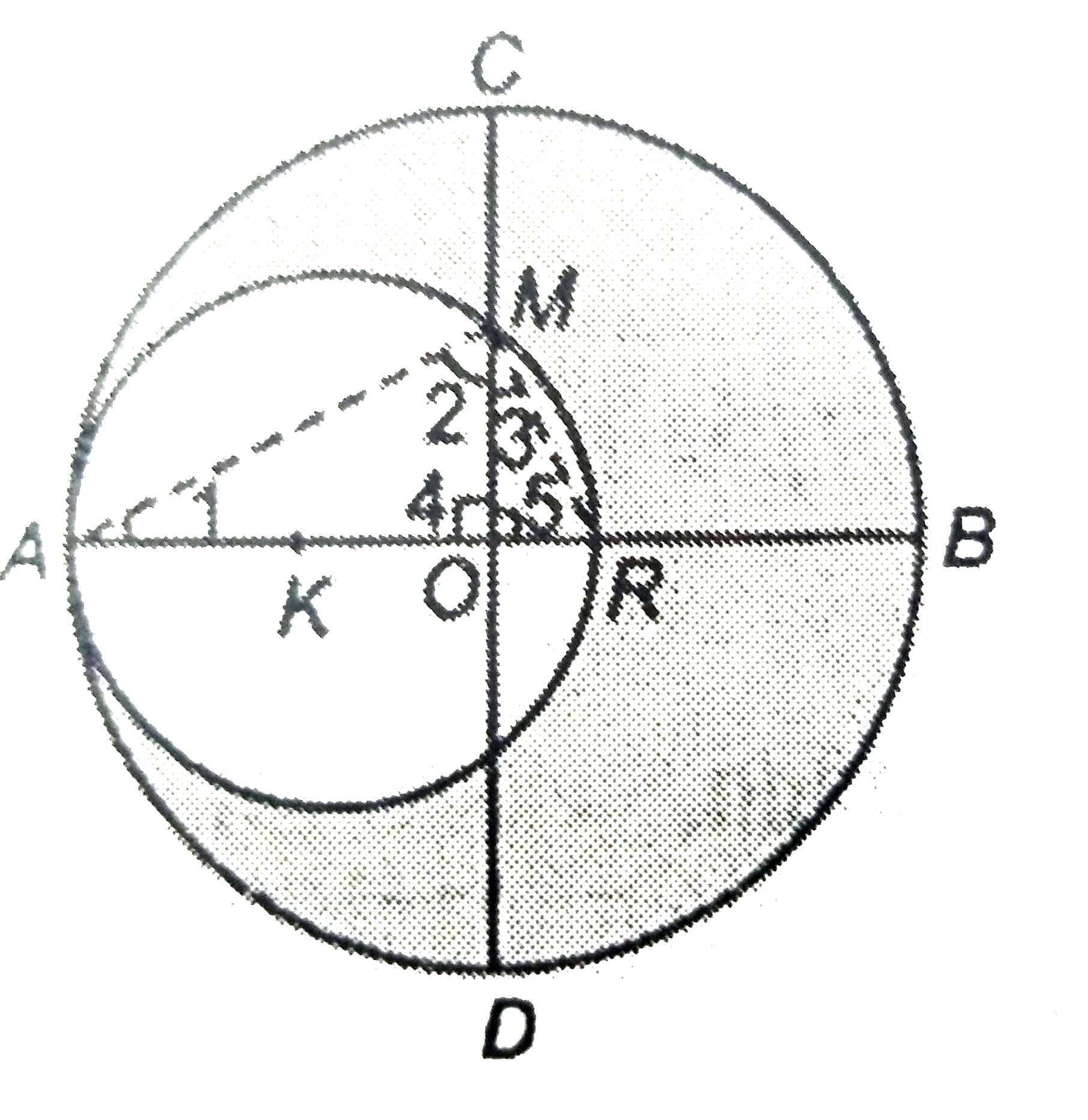
View SolutionIn the adjoining figure, CM = 5 cm, RB = 9 cm, , O is the centre of larger circle and K is the centre of smaller circle. Find the area of shaded region

View SolutionIn Figure, a crescent is formed by two circles which touch at A. C is the centre of the larger circle. The width of the crescent at BD is 9cm and at EF it is 5cm. Find (i) the radii of two circles (ii) the area of the shaded region.
View SolutionIn Figure, a crescent is formed by two circles which touch at A. C is the centre of the larger circle. The width of the crescent at BD is 9cm and at EF it is 5cm. Find (i) the radii of two circles (ii) the area of the shaded region.
View SolutionThe shaded portion of the figure, given alongside, shows two concentric circles.
If the circumference of the two circles be 396 cm and 374 cm, find the area of the shaded portion.

View SolutionIn the adjoining figure circles with centres A and C touch internally at point T . Line AB is tangent to the smaller circle at point P . Point B lies on the bigger circle. Radii are 16 cm and 6 cm . Find AP.
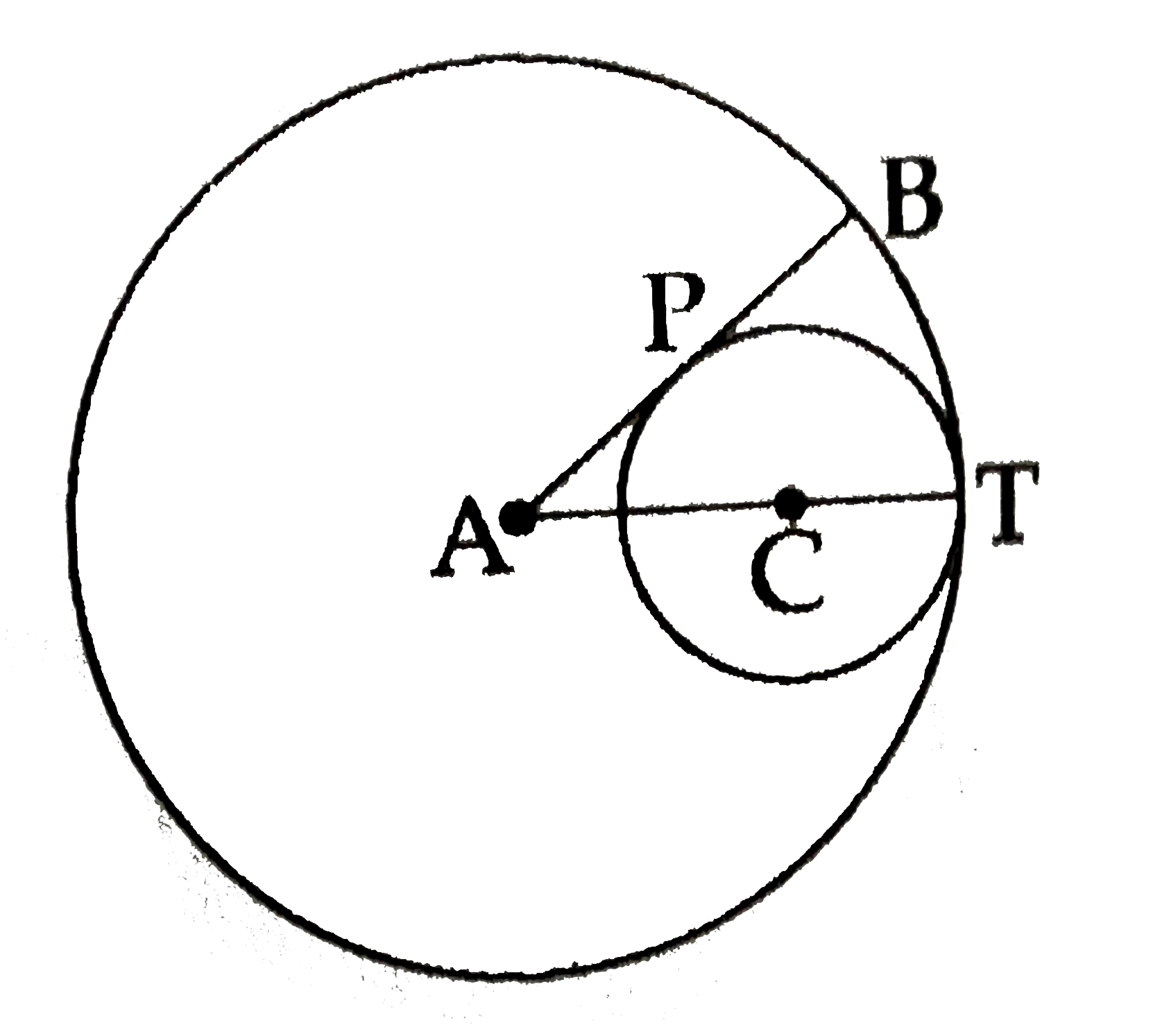
View SolutionIn the adjoining figure circles with centres A and C touch internally at point T. Line AB is tangent to the smaller circle at point P. Point B lies on the bigger circle. Radii are 16 cm and 6 cm. Find AP.
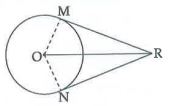
View SolutionIn the adjoining figure, O is the centre of the circle. From point R, seg RM and RN are tangent segments drawn which touch the circle at M, N. If OR=10 cm, radius of the circle=5 cm, then find m
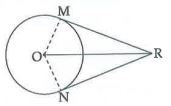
View SolutionIn the adjoining figure, O is the centre of the circle. From point R, seg RM and RN are tangent segments drawn which touch the circle at M, N. If OR=10 cm, radius of the circle=5 cm, then find m
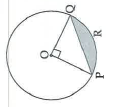
View SolutionIn the adjoining figure, if O is the centre of the circle, PQ is a chord. , area of shaded region is 114 , find the radius of the circle
View SolutionIn the adjoining figure, O is the centre of the circle with AC = 24 cm, AB = 7 cm and . Find the area of the shaded region.
View SolutionIn the adjoining figure, O is the centre of the circle with AC = 24 cm, AB = 7 cm and . Find the area of the shaded region.
View SolutionIn the given figure, two circles touch each other internally at point P., where Q is the centre of larger circle. If RS = 17 cm, TU = 9 cm and TV_|_ RP , then find the area of shaded region.
View SolutionIn the figure, two circles with centres O and P are touching internally at point A. If BQ = 9, DE = 5, complete the following activity to find the radii of the circles :
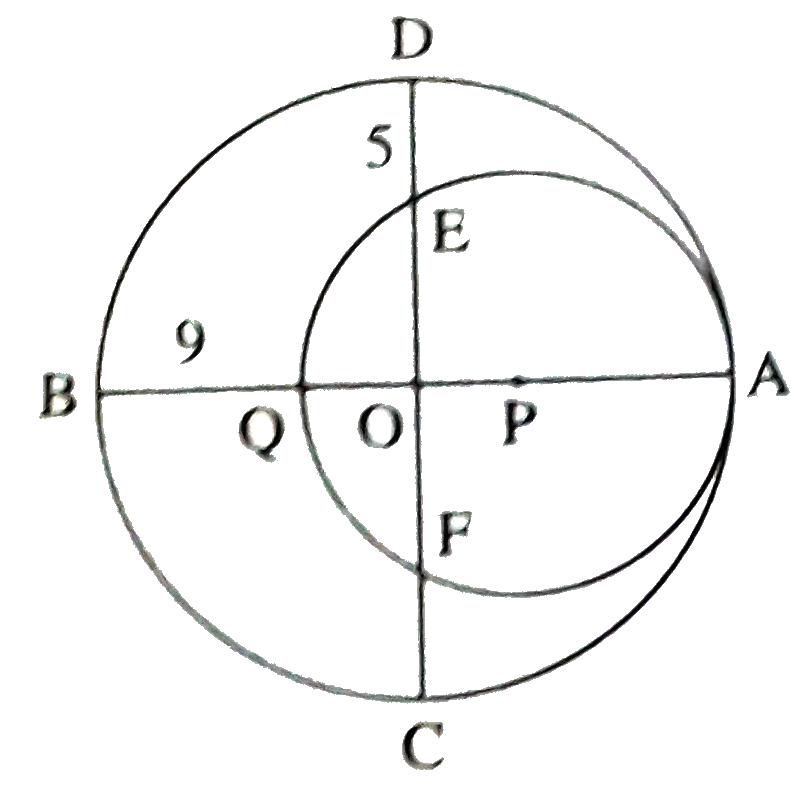
View SolutionIn the given figure, two circle with centres O and P are touching internally at point A.
If BQ= 9, DE= 5, complete the following activity to find the radii of the circle.
View SolutionIn the figure, the area of the shaded portion is 770 . If the circumference of the outer circle is 132 cm, find the width of the shaded part

View SolutionIn the following figure, three circles are given. The two smaller circles are equal. The radius of the larger circle is 8 cm. O is the centre or the larger circle. Find area of shaded portion.
View SolutionIn the adjoining figure, point 'O' is the centre of the circle, m (arc PQR) = , OP = 10 cm. Find the area of the shaded portion.
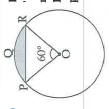
View SolutionIn the adjoining figure, two circles cut at A and B. P and Q are the centres of the circles. If , then find the area of the shaded portion if AP = 4 cm. (Use )
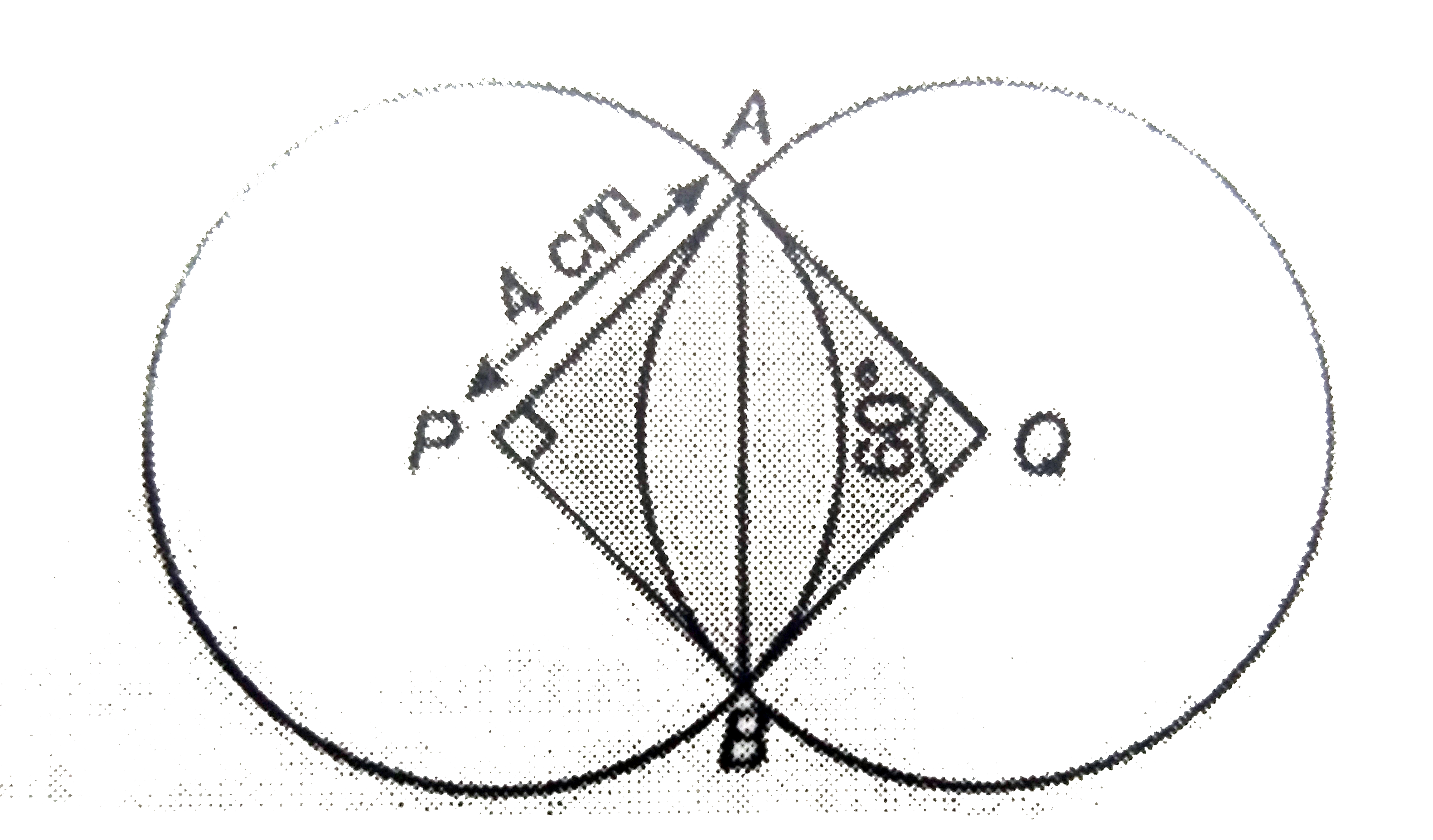
View Solution