In the adjoining figure, O is the centre of the circle with AC = 24 cm, AB = 7 cm and ∠BOD=90∘. Find the area of the shaded region.
To find the area of the shaded region in the given problem, we will follow these steps:
Step 1: Identify the given values
- AC = 24 cm
- AB = 7 cm
- ∠BOD = 90°
Step 2: Use the Pythagorean theorem to find BC
Since triangle ABC is a right triangle (∠CAB = 90°), we can apply the Pythagorean theorem:
BC2=AB2+AC2
Substituting the values:
BC2=72+242
BC2=49+576
BC2=625
Taking the square root:
BC=√625=25 cm
Step 3: Find the radius of the circle
Since BC is the diameter of the circle:
Radius(r)=BC2=252=12.5 cm
Step 4: Calculate the area of the circle
Using the formula for the area of a circle:
Area of circle=πr2
Substituting the radius:
Area of circle=227×(12.5)2
Calculating (12.5)2:
(12.5)2=156.25
Now substituting back:
Area of circle=227×156.25=491.07 cm2
Step 5: Calculate the area of triangle ABC
Using the formula for the area of a triangle:
Area of triangle=12×base×height
Here, base = AB and height = AC:
Area of triangle=12×7×24
Calculating:
Area of triangle=12×168=84 cm2
Step 6: Calculate the area of sector BOC
Using the formula for the area of a sector:
Area of sector=θ360×πr2
Here, θ=90∘:
Area of sector=90360×227×(12.5)2
Calculating:
Area of sector=14×491.07=122.77 cm2
Step 7: Find the area of the shaded region
The area of the shaded region can be calculated by subtracting the area of triangle ABC and adding the area of sector BOC from the area of the circle:
Area of shaded region=Area of circle−Area of triangle+Area of sector
Substituting the values:
Area of shaded region=491.07−84+122.77
Calculating:
Area of shaded region=491.07−84+122.77=529.84 cm2
Final Answer
The area of the shaded region is approximately:
Area of shaded region≈529.84 cm2
- AC = 24 cm
- AB = 7 cm
- ∠BOD = 90°
Since triangle ABC is a right triangle (∠CAB = 90°), we can apply the Pythagorean theorem:
BC2=AB2+AC2
Substituting the values:
BC2=72+242
BC2=49+576
BC2=625
Taking the square root:
BC=√625=25 cm
Since BC is the diameter of the circle:
Radius(r)=BC2=252=12.5 cm
Using the formula for the area of a circle:
Area of circle=πr2
Substituting the radius:
Area of circle=227×(12.5)2
Calculating (12.5)2:
(12.5)2=156.25
Now substituting back:
Area of circle=227×156.25=491.07 cm2
Using the formula for the area of a triangle:
Area of triangle=12×base×height
Here, base = AB and height = AC:
Area of triangle=12×7×24
Calculating:
Area of triangle=12×168=84 cm2
Using the formula for the area of a sector:
Area of sector=θ360×πr2
Here, θ=90∘:
Area of sector=90360×227×(12.5)2
Calculating:
Area of sector=14×491.07=122.77 cm2
The area of the shaded region can be calculated by subtracting the area of triangle ABC and adding the area of sector BOC from the area of the circle:
Area of shaded region=Area of circle−Area of triangle+Area of sector
Substituting the values:
Area of shaded region=491.07−84+122.77
Calculating:
Area of shaded region=491.07−84+122.77=529.84 cm2
The area of the shaded region is approximately:
Area of shaded region≈529.84 cm2
Topper's Solved these Questions
- AREA RELATED TO CIRCLESBook:NAGEEN PRAKASHAN ENGLISHChapter:AREA RELATED TO CIRCLESExercise:Problems From NCERT /exemplar
Explore 25 Videos
- AREA RELATED TO CIRCLESBook:NAGEEN PRAKASHAN ENGLISHChapter:AREA RELATED TO CIRCLESExercise:Exercise 12 A
Explore 24 Videos
- ARITHMETIC PROGRESSIONBook:NAGEEN PRAKASHAN ENGLISHChapter:ARITHMETIC PROGRESSIONExercise:Revision Exercise Long Answer Question
Explore 5 Videos
Similar Questions
In Figure , O is the centre of the circle with AC = 24 cm, AB = 7 cm and ∠BOD=90°. Find the area of the shaded region.[Useπ=3⋅14]
View SolutionIn Figure 6, O is the centre of the circle with AC = 24 cm, AB = 7 cm and ∠BOD=90°. Find the area of the shaded region.[Useπ=3⋅14]

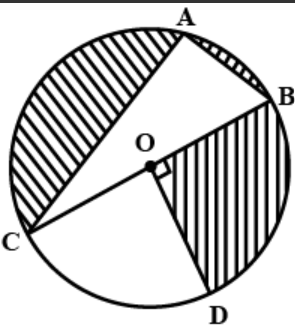
View SolutionIn the adjoining figure , O is the centre of the circle. If ∠ACB=25∘, then find ∠AOB.
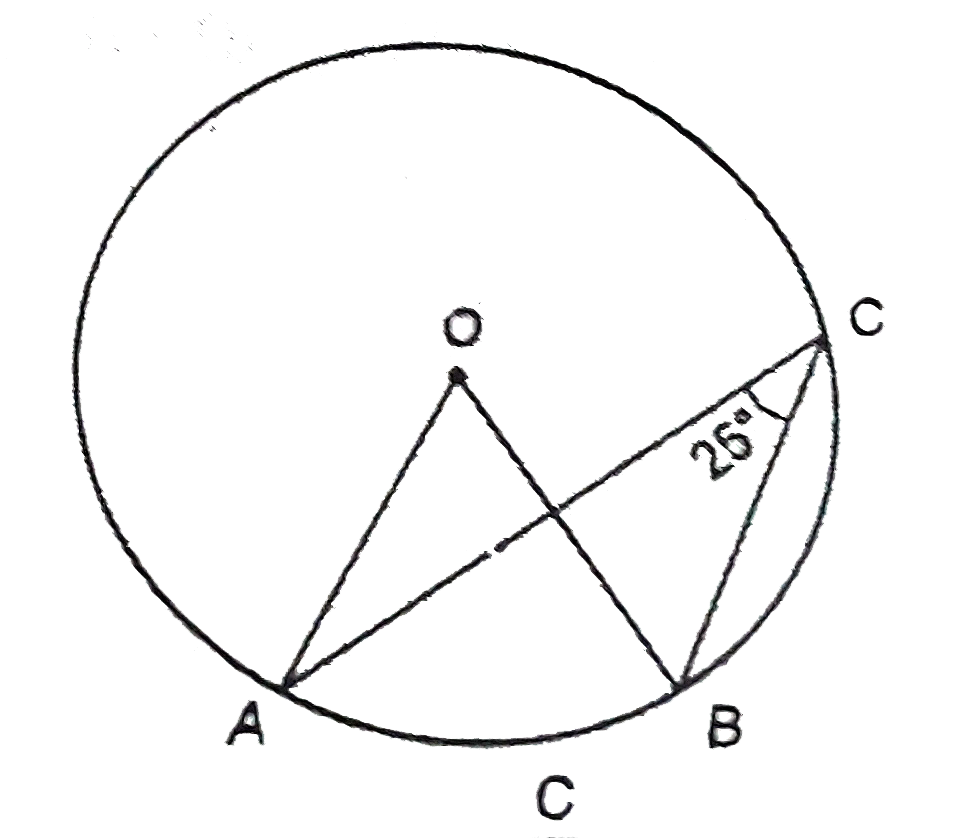
View SolutionIn the adjoining figure, O is the centre of the circle. Find the value of ∠BEC.
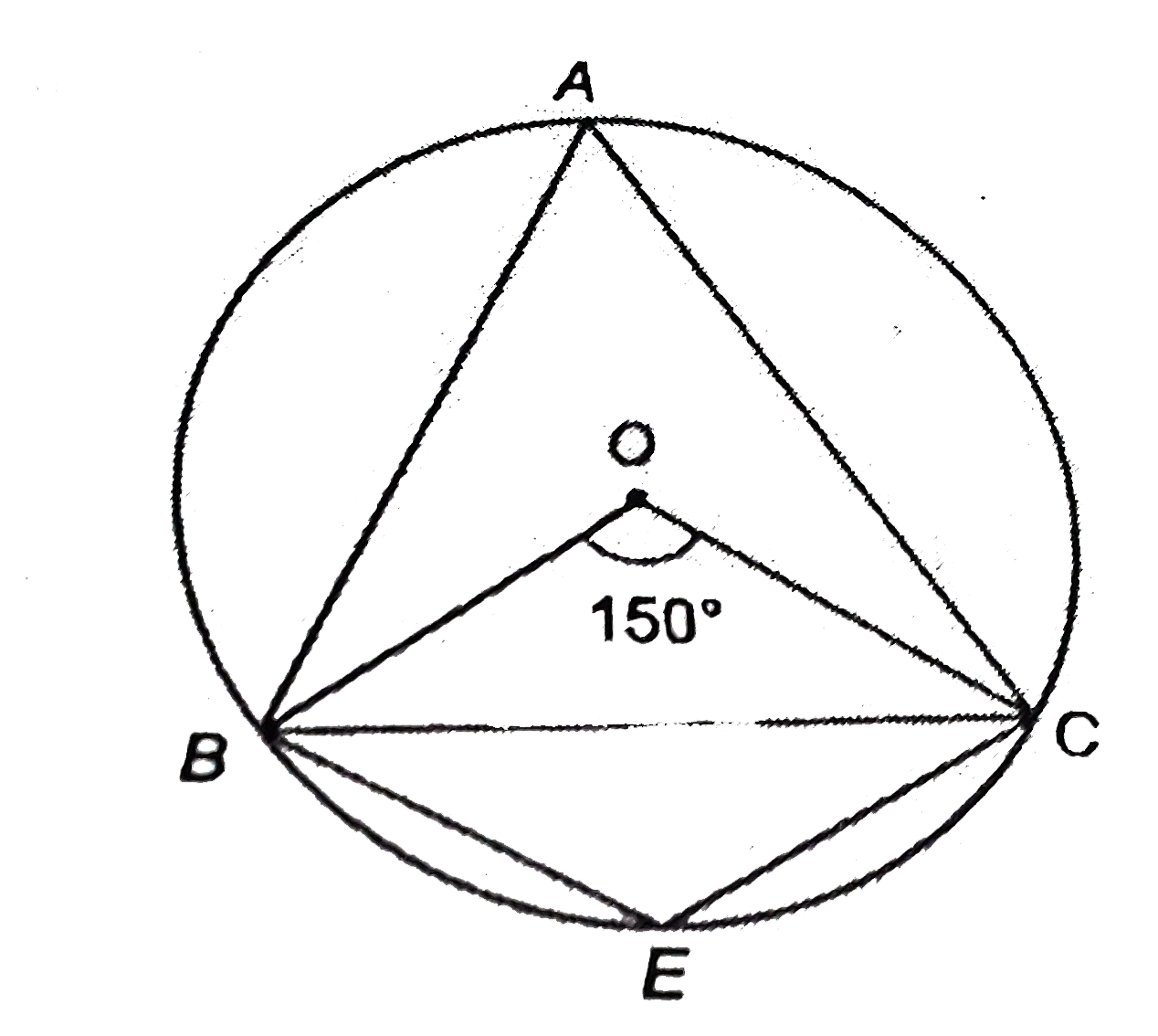
View SolutionIn the adjoining figure , O is the centre of the circle and ∠OAB=60∘. Find ∠APC.

View SolutionIn the adjoining figure, two concentric circle with centre O have radii 21 cm and 42 cm. If ∠AOB=60∘, find the area of the shaded region. (Use π=227)

View SolutionIn the adjoining figure, O is the centre of the circle and AB is its diameter. If AC=8 cm and BC= 6cm, then find the radius of the circle.

View SolutionIn the adjoining figure, O is the centre of the circle.If ∠BAC=40∘, then find the value of ∠ADC.

View SolutionIn the adjoining figure O is the centre of the circle . If chord AB=2 cm radius OA=2 cm, then find the value of ∠ACB.

View SolutionIn the adjoining figure, O is the centre of the circle and AC is its diameter. If ∠BAC=30∘, then find ∠BOC.
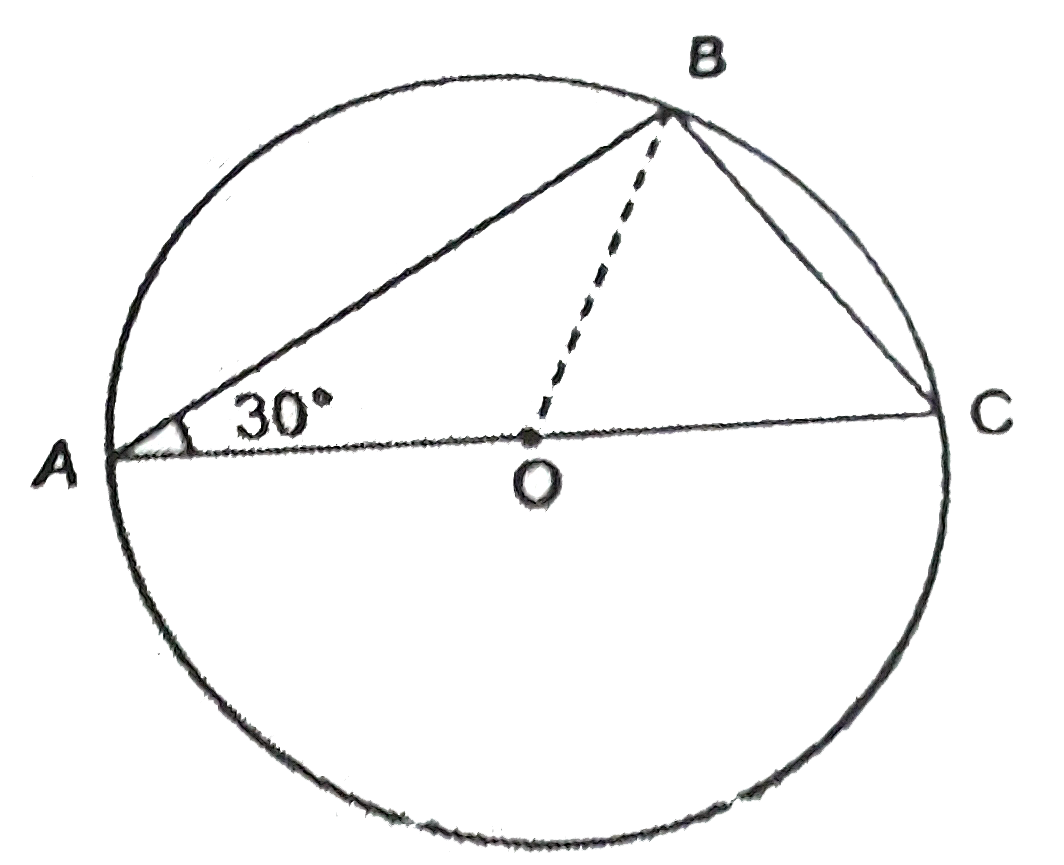
View Solution