In ΔABC if AD is the bisector of ∠A prove that Area ΔABD/Area ΔACD =AB/AC
In ΔABC AD is the bisector of ∠A.Hence Proved.
Related Solutions
The medians of a triangle ABC intersect each other at point G. If one of its medians is AD, Prove that :
(i)
(ii)
(iii)
View SolutionIn , if is the bisector of , prove that:
View Solutionमें, का समद्विभाजक है । जो BC से D पर मिलती है, तो सिद्ध करें कि
View SolutionIn A AB = 10 AC = 18 AD is angle bisector If area of is 28 . find area of ADB ?
View SolutionΔABC is isosceles with AB=AC=7cm and BC=9cm. The height AD from A to BC, is 6cm. Find the area of ΔABC. What will be the height from C to AB i.e., CE?
View SolutionProve that E is a point E but V (ABE) = V (ACE) on the AD equation of ΔABC in Figure 11.23?
View Solutionतथा AD, का समद्विभाजक है | सिध्द करो कि .
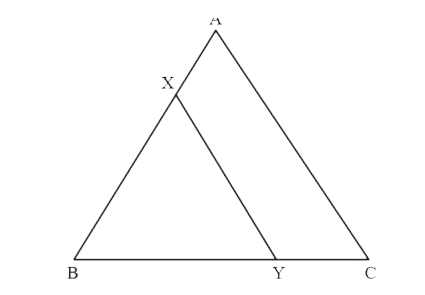
View SolutionIn the given figure, the line segment XY is Parallel to AC of ΔABC and it divides the triangle into two parts of equal areas. Prove that
View SolutionABC is a right triangle such that AB=AC and bisector of angle C intersects the side AB at D. prove that AC+AD=BC.
View SolutionABC is a triangle in which AB = AC = 4 cm and .Calculate Area of ΔABC
View SolutionIn a is angle bisector . If the area of . Find area of
View SolutionD is a point on side BC ΔABC such that AD = AC (see figure). Show that AB > AD.
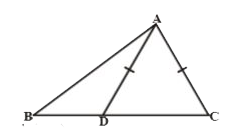
View SolutionD is a point on side BC ΔABC such that AD = AC (see figure). Show that AB > AD.
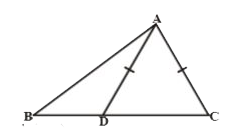
View SolutionD is a point on side BC ΔABC such that AD = AC (see figure). Show that AB > AD.
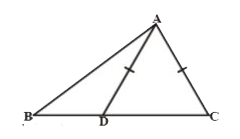
View SolutionD is a point on side BC ΔABC such that AD = AC (see figure). Show that AB > AD.
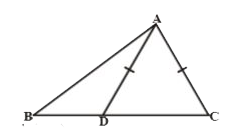
View SolutionIn the figure, ΔABC and ΔABD are two triangles on the same base AB. If line segment CD is bisected by at O, show that ar
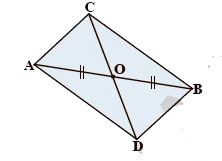
View SolutionIn the figure, ΔABC and ΔABD are two triangles on the same base AB. If line segment CD is bisected by at O, show that ar
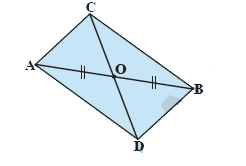
View SolutionIn the figure, ΔABC and ΔABD are two triangles on the same base AB. If line segment CD is bisected by at O, show that ar
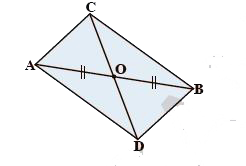
View SolutionDeltaABC Of angleA The bisector of AD is AD, P is any single point on AD Prove that the lengths inserted from AB to AC and AC from P are equal.
View SolutionABC is a right angled triangle, in which AB = AC and angle C The bisector arm of AB intersects AB at D. Prove that AC+AD=BC is.
View Solution