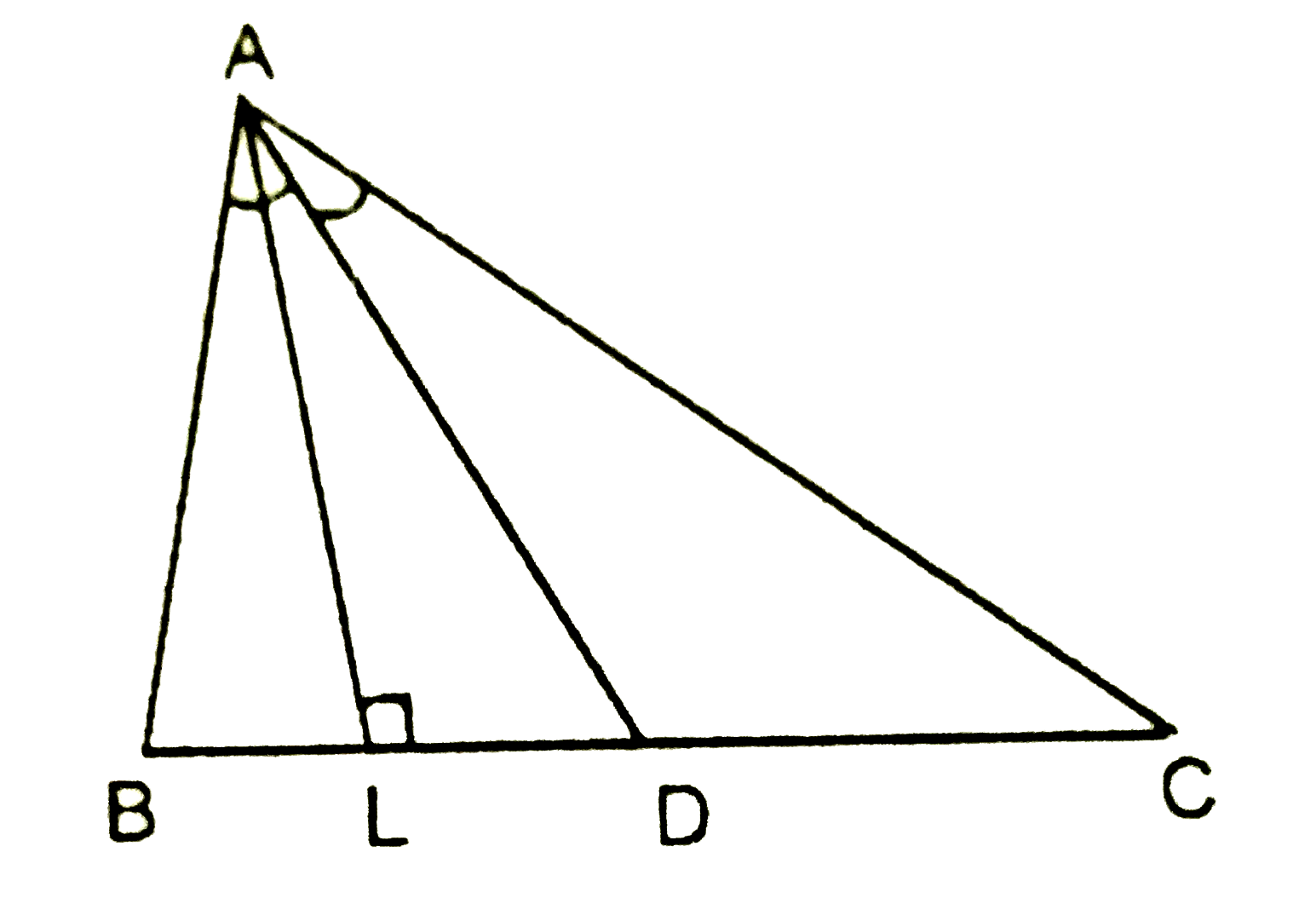
ΔABC में, AD∠BAC का समद्विभाजक है । जो BC से D पर मिलती है, तो सिद्ध करें कि ar(ΔABD)ar(ΔACD)=ABAC
दिया है : ΔABC में , AD∠BAC का अर्द्धक है जो BC से D पर मिलती है ।
सिद्ध करना है कि : क्षे(ΔABD)क्षे(ΔACD)=ABAC
रचना : (हम AL⊥BC खींचा
उपपत्ति : चूँकि AD,∠BAC का समद्विभाजक है ।
∴ABAC=BDDC .....(i)
अब क्षे(ΔABD)क्षे(ΔACD)=12BD×AL12DC×AL=BDDC....(ii)
(i) और (ii) से हम पाते है,
क्षे(ΔABD)क्षे(ΔACD)=ABAC (प्रमाणित)
Topper's Solved these Questions
- त्रिभुज BOOK - KC SINHACHAPTER - त्रिभुज EXERCISE - EXCERCISE 6.1
22 Videos
- त्रिभुज BOOK - KC SINHACHAPTER - त्रिभुज EXERCISE - EXCERCISE 6.2 (अतिलघु उत्तरीय प्रश्न )
8 Videos
- त्रिकोणमितीय अनुपात और सर्वसमिकाएँ BOOK - KC SINHACHAPTER - त्रिकोणमितीय अनुपात और सर्वसमिकाएँ EXERCISE - EXERCISE 8.4
85 Videos
- दो चर वाले रैखिक समीकरण युग्मBOOK - KC SINHACHAPTER - दो चर वाले रैखिक समीकरण युग्मEXERCISE - वस्तुनिष्ठ प्रश्न
44 Videos
Similar Questions
कोष्ठक में दिए उपयुक्त शब्द से रिक्त स्थानों को भरें :
2 cm भुजा वाले सभी वर्ग ................. होते है । (सद्रश्य , सर्वागसम , सद्रश्य और सर्वागसम दोनों)
View SolutionΔABC में ,P और AB क्रमशः AB तथा AC पर दो बिन्दु इस प्रकार है कि PQ∣∣BC और APPB=23 तो AQQC का मान ज्ञात करें ।
View Solutionरिक्त स्थानों की पूर्ति करें :
sin2θ+cos2θ= ……………..
View Solutionयदि a1b2≠a2b1 तब समीकरण निकाय a1x+b1y+c1=0,a2x+b2y+c2=0 का
View SolutionΔABC में BC पर एक बिंदु D इस प्रकार है कि BD:DC=m:n है |
सिद्ध करें कि ar(ΔABD):ar(ΔACD)=m:n
View SolutionA circle is inscribed in triangle ABC , touching AB at P, BC at Q and AC at R. If AR=5 cm, RC= 6 cm and AB=12 cm, then perimeter of triangle ABC is: एक वृत्त किसी त्रिभुज ABC में समाहित है जो AB को P पर, BC को Q पर तथा AC को R पर स्पर्श करता है | यदि AR =5 सेमी और AB = 12 सेमी है, तो त्रिभुज ABC का परिमाप ज्ञात करें |
View Solutiontriangle ABC ~ triangle RQP and AB = 4 cm , BC = 6 cm and AC = 5 cm. If ar(triangle ABC) : ar (triangle PQR)=9:4 , then PQ is equals to : triangle ABC ~ triangle RQP है तथा AB = 4 सेमी, BC = 6 सेमी और AC = 5 सेमी है | यदि ar(triangle ABC) : ar (triangle PQR)=9:4 ,है, तो PQ किसके बराबर है ?
View SolutionIn a triangle ABC , AD is perpendicular to BC from A, if angle BAC = 90^@ , then AB^2:AC^2 is equal to : त्रिभुज ABC में, AD, A से BC पर डाला गया लम्ब है | यदि angle BAC = 90^@ है, तो AB^2:AC^2 का मान क्या होगा ?
View SolutionIn triangle ABC ,AD bisects angle A which meets BC at D. If BC = a, AC = b and AB = c, then DC = ? त्रिभुज ABC में, AD कोण A को द्विभाजित करता है जो BC से D पर मिलता है | यदि BC = a, AC = bऔर AB = c है, तो DC = ?
View Solutiontriangle ABC ~ triangle EDF and AB =5 cm, BC = 8cm and AC = 10cm.If ar(triangle ABC) : ar(triangle EDF) = 9: 4 ,then DF is equal to: triangle ABC ~ triangle EDF है तथा AB = 5cm, BC = 8cm और AC = 10cm है| यदि ar(triangle ABC) : ar(triangle EDF) = 9: 4 ,है, तो DF का मान क्या होगा ?
View SolutionIn triangle ABC , AD is median and G is the point on AD such that AG: GD = 2: 1, then ar(triangle ABG) :ar(triangle ABC) is equal to : त्रिभुज ABC में, AD मध्यिका है तथा G, AD पर स्थित ऐसा बिंदु है कि AG: GD = 2 : 1 है, तो ar(triangle ABG) :ar(triangle ABC) का मान किसके बराबर होगा ?
View SolutionIn triangle ABC , AD is median and P is the point on AD such that AP : PD = 3 : 4, then ar(triangle APB) :ar(triangle ABC) is equal to : त्रिभुज ABC में, AD मध्यिका है तथा P, AD पर स्थित ऐसा बिंदु है कि AP : PD = 3 : 4 है, तो ar(triangle APB) :ar(triangle ABC) का मान किसके बराबर होगा ?
View SolutionIn triangle ABC ,AD is a median and P is a point on AD such that AP : PD = 3 : 4. Then ar (triangle BPD): ar (triangle ABC) is equal to: त्रिभुज ABC में, AD एक माध्यिका है और P, AB पर स्थित ऐसा बिंदु है कि AP : PD = 3 : 4 है| ar (triangle BPD): ar (triangle ABC) ज्ञात करें |
View SolutionIn triangle ABC ,P is a point on BC such that BP : PC = 1 : 2 and Q is the mid point of BP. then, ar(triangle ABQ) :ar (triangle ABC) is equal to: त्रिभुज ABC में, P, BC पर स्थित ऐसा बिंदु है कि BP : PC = 1 : 2 है और Q, BP का मध्य बिंदु है | तो ar(triangle ABQ) :ar (triangle ABC) का मान क्या होगा ?
View SolutionIn △ABC ,P is a point on BC such that BP : PC = 3 : 4 and Q is the midpoint of BP. Then ar(△ABQ):ar(△ABC) is equal to:
त्रिभुज ABC में, P, BC पर स्थित एक ऐसा बिंदु है कि BP : PC = 3 : 4 है और Q, BP का मध्य बिंदु है | ar(△ABQ):ar(△ABC) का मान ज्ञात करें |
View Solution
