PRACTICAL GEOMETRY for Class 6 MATHS
The Circle
Bacco, Circles are everywhere around us. A ball, a pizza, a pie, a wheel, a plate, a coin, and so on are a few circular objects that we come across in our daily life.. Every point on a circle's boundary is at an equal distance from its Centre.
Let's learn how to Construct a circle when its radius is known.
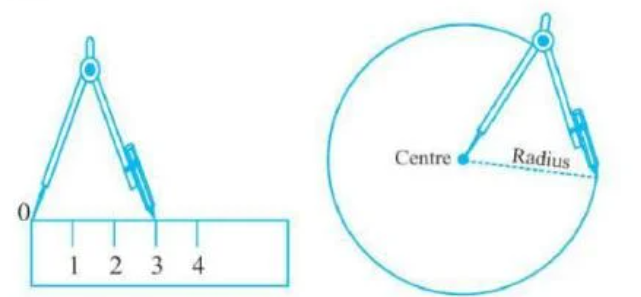
A Line Segment
In geometry, it's a common mistake to say a segment and a line are one and the same.
A segment has a definite beginning and a definite end, with each end represented by a point.
Examples of segments include the length of a table, the distance of a straight road, etc.
On the other hand, a line has no definite beginning or end.
A segment is a part of a line that has a fixed length or we can say that both the ends of a segment are fixed.Segments, sometimes also referred to as line segments.
Let's see the construction of a line segment of a given length using compass and ruler.
Step 1: Draw a line of any length.
Step 2: Mark the starting point of the line segment as point A.
Step 3: Take a ruler and place the pointer of the compass at A, open the compass, say 6cm apart from the pencil’s lead.
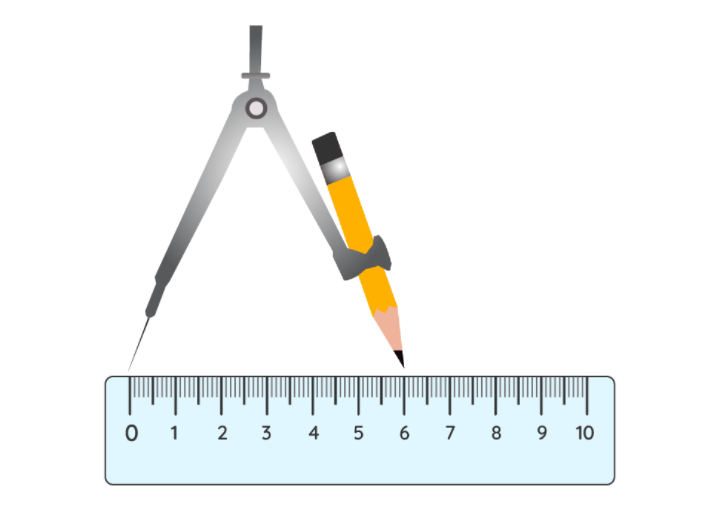
Step 4: Mark an arc on the line with the pencil point.
Step 5: Mark the intersection point of the arc and line as point B.
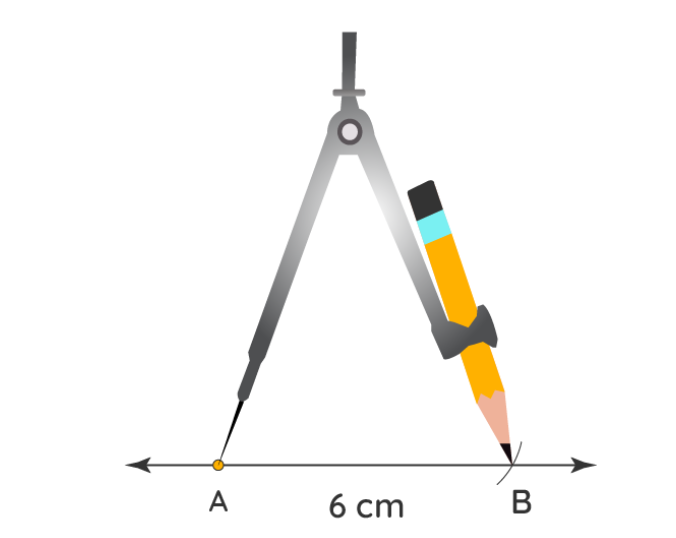
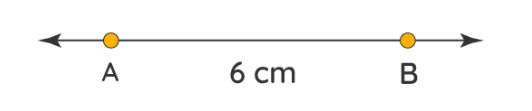
Step 6: AB is the required line segment of length 6cm.
Tips and Tricks
Baccho, suppose ki aapko ek line segment given hai and aapko uski length nahi pata. How can you construct a copy of the same line segment in this given situation?
Some easy methods are:
But these are not the accurate methods of constructing a copy of a line segment. The most accurate method is as follows:
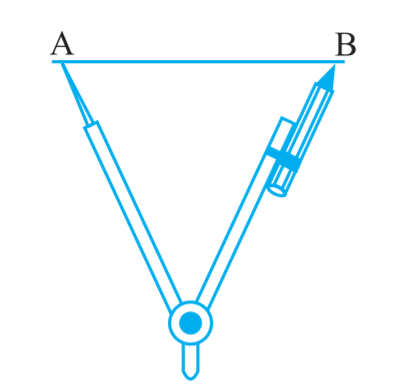
Step 1:Given AB whose length is not known.

Step 2: Fix the compasses pointer on A and the pencil end on B. The opening of the instrument now gives the length of AB.
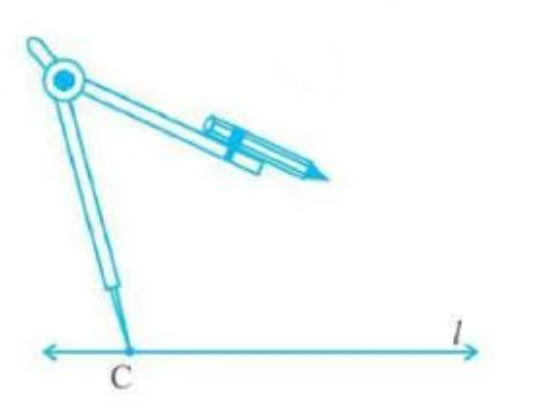
Step 3: Draw any line l. Choose a point C on l. Without changing the compasses setting, place the pointer on C.
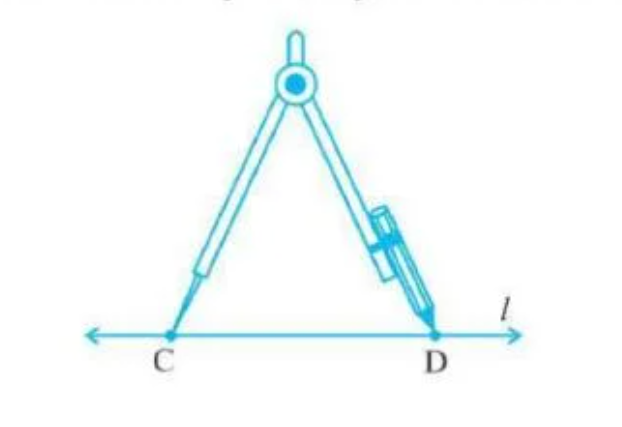
Step 4: Swing an arc that cuts l at a point, say, D. Now CD is a copy of AB.
Example 1
Construct line segments whose lengths are:
4.8cm
(iii)7.6cm
Please refer to the given video solution.
Perpendiculars
Baccho, ek perpendicular tab form hota hai jab do lines ya line segments ek dusre ko 90∘ k angle p intersect krti hai. Let's learn how to construct a perpendicular on a given line segment using ruler and compass.
Baccho phle hum dekhenge ki hum perpendiculars kaise construct kr skte hai jo ki given point se pass ho.
Perpendicular to a line through a point on it
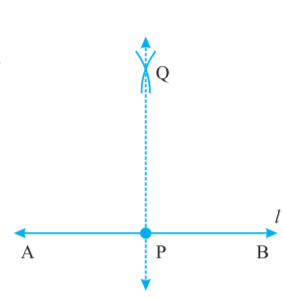
Step 1: Given a point P on a line l.
Step 2: With P as centre and a convenient radius, construct an arc intersecting the linel at two points A and B.
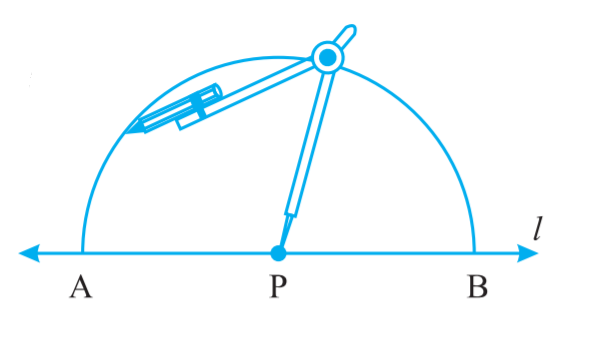
Step 3: With A and B as centres and a radius greater than AP construct two arcs, which
cut each other at Q.

Step 4: Join PQ. Then PQ is perpendicular to l. We write PQ⊥l.
Perpendicular to a line through a point not on it
Step 1: Given a line l and a point P not on it.
Step 2: With P as centre, draw an arc which intersects line l at two points A and B.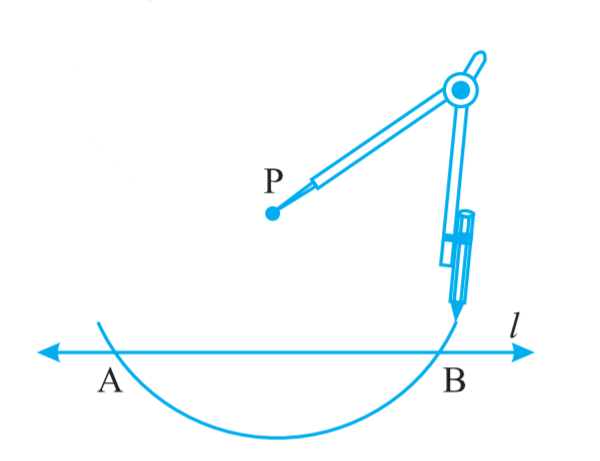
Step 3: Using the same radius and with A and B as centres, construct two arcs that intersect at a point, say Q, on the other side.
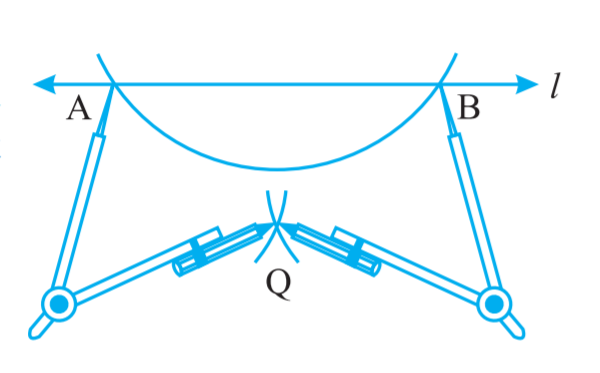
Step 4: Join PQ. Thus, PQ is perpendicular to l.

The perpendicular bisector of a line segment
Baccho ab hum seekhenge ki agar hume ek line segment given ho to hum uska perpendicular bisector kaise construct kr skte hai. Perpendicular bisector vo line segment hoti hai jo ki ek dusri line segment ko 90∘ k angle p bisect krti hai, yaani ki exactly two equal halves m divide krti hai.
Suppose we have a line segment AB.

Step 1: Taking A and B as centers, and a radius of more than half of AB, draw arcs on both sides of AB, to intersect each other, as shown below.
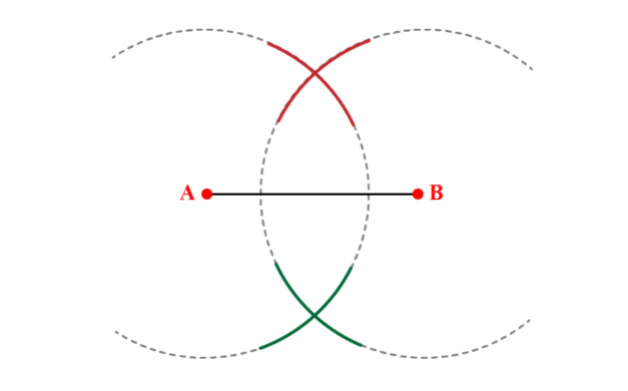
The reason you require the radius of your arcs to be more than half of AB is that if the radius is less than half of AB, the arcs will not intersect (try it!).
Step 2: Let the two points of the intersection so obtained be P and Q. Draw a line through P and Q. This is the required perpendicular bisector.
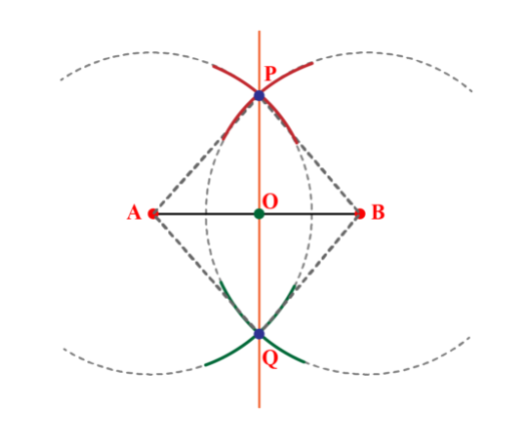
Here, POQ is the perpendicular bisector of AB.
Example 2
Draw a line segment AB of lineth 10cm. Mark a point P on AB such that AP=4cm. Draw a line through P perpendicular to AB.
Please refer to the given video solution.
Example 3
Draw a line segment PQ of length 12cm. Mark a point O outside this segment. Draw a line through O perpendicular to PQ.
Please refer to the given video solution.
Angles
Baccho, jab bhi do line segments intersect krte hai to ek angle form hota hai. It can range between 0∘−360∘. The construction of angles is one of the most important aspects of geometry and is the "pure" form of geometric construction. The term construction in geometry refers to drawing shapes, lines, or angles accurately with the help of mathematical instruments.
In section m hum pdhenge ki angles and angle bisectors ko kaise draw kia jaata hai.
Constructing an angle of a given measure
Step 1 - Draw a line segment OA.
Step 2 - Place the center of the protractor at point O.
Step 3 - Starting from point A in the clockwise direction and mark a point at 50 degrees by looking at the outer circle of the protractor. Label this point as B. The ∠BOA is the required 50∘ angle.
IMAGE 20
2 Constructing a copy of an angle of unknown measure
Given ∠A , whose measure is not known.
Step 1: Draw a line l and choose a point P on it.
IMAGE 21
IMAGE 22
Step 2: Place the compasses at A and draw an arc to cut the rays of ∠A at B and C.
IMAGE 23
Step 3: Use the same compasses setting to draw an arc with P as centre, cutting l in Q.
IMAGE 24
Step 4: Set your compasses to the length BC with the same radius.
IMAGE 25
Step 5: Place the compasses pointer at Q and draw the arc to cut the arc drawn earlier in R.
IMAGE 26
Step 6: Join PR. This gives us ∠P . It has the same measure
as ∠A. This means ∠QPR has same measure as ∠BAC.
IMAGE 27
Bisector of an angle
An angle bisector is a line that bisects or divides an angle into two equal halves.
Follow the sequence of steps mentioned below to construct an angle bisector.
Step 1: Span any width of radius in a compass and with O as the center, draw two arcs such that it cut the rays OA and OB at points C and D respectively.
IMAGE 28
Note that OC=OD, since these are radii of the same circle.
Step 2: Without changing the distance between the legs of the compass, draw two arcs with C and D as centers, such that these two arcs intersect at a point named E (in the image).
IMAGE 29
Note that CE=DE, since the two arcs were drawn in this step was of the same radius.
Step 3: Join the ray OE. This is the required angle bisector of angle AOB.
IMAGE 30
Angles of special measures
Baccho aapne already 90∘ ka angle construct krna seekhlia hai jab aap perpendiculars draw krna seekh rhe the. Ab hum seekhenge ki hum specific measures k angles kaise construct kr skte hai using a compass and a ruler. We will learn the construction of 60∘,30∘ and 120∘ angle in this section.
Constructing a 60∘ angle
Suppose that you have a line L and some point A on L just like shown in the figure.
IMAGE 31
Now let us try to construct a ray (or line) through A which is inclined at 60∘ to L.
Step 1: Taking A as a center, place the needle of a compass on A and draw an arc of any radius length that intersects L at B as shown in the figure below.
IMAGE 32
Step 2: Now, taking B as center and AB as radius, draw another arc that intersects the first arc at C:
IMAGE 33
Step 3: Draw a ray (or line) through A and C. This will be inclined at 60∘ to L:
IMAGE 34
Here, AB=AC, since these are radii of the same circular arc. Also, BC=BA, since these too are radii of the same (second) circular arc. Thus, AB=BC=AC. This means that triangle ABC is equilateral, and so, angle BAC=60∘.
Constructing a 30° angle
Note that by bisecting an angle of 60∘, we can construct an angle of 30∘, and further by bisecting an angle of 30∘ we can construct an angle of 15∘.
Constructing a 120° angle
Step 1: Draw a line segment AB.
Step 2: With A as a center and draw an arc of proper length.
IMAGE 35
Step 3: Take D as a center with the same radius, draw two marks E and F on the former arc.
Step 4: Join points A to F and produce to point C. Thus ∠CAB=120∘.
Example 4
Using a protractor, draw ∠BAC of measure 450. Take a point P in the interior of ∠BAC. From P draw line segments PM and PN such that PM⊥AB and PN⊥AC, Measure ∠MPN.
Please refer to the given video solution.
Example 5
Draw a line segment PQ of length 8.4cm. Draw the perpendicular bisector of this line segment.
Please refer to the given video solution.
Example 6
Construct a rectangle whose adjacent sides are 8cm and 3cm.
Please refer to the given video solution.
SUMMARY
This chapter deals with methods of drawing geometrical shapes
1. We use the following mathematical instruments to construct shapes:
(i) A graduated ruler
(ii) The compasses
(iii) The divider
(iv) Set-squares
(v) The protractor
2. Using the ruler and compasses, the following constructions can be made:
(i) A circle, when the length of its radius is known.
(ii) A line segment, if its length is given.
(iii) A copy of a line segment.
(iv) A perpendicular to a line through a point:(a) on the line (b) not on the line.
(v) The perpendicular bisector of a line segment of given length.
(vi) An angle of a given measure.
(vii) A copy of an angle.
(viii) The bisector of a given angle.
(ix) Some angles of special measures such as
(a)90∘
(b)45∘
(c)60∘
(d)30∘
(e)120∘
(f)135∘
Let's Revise
1. Baccho iss chapter m humne geometric constructions k baare m seekha.
2.Humne seekha ki hum line segments ko kaise construct kr skte. We also learnt how to construct copies of given line segments.
3. Baccho, humne circles construct krna bhi seekha. We learnt how we can construct circles of given radius.
4. Perpendiculars vo line segments hote hai jo ki dusre line segment ko 90∘ k angle p intersect krti hai.
5. Humne perpendiculars construct krne k alag alag methods seekhe jisme agar hume specific points given ho to hum unhe kaise construct kr skte hai. we also learnt how to draw perpendicular bisectors of given line segments.
6. Geometry ek bohot hi important tool hota hai humari daily life m aur geometry m angles are also extremely important.
7. Humne seekha ki hum kisi bhi measure k angle ko protractor se use krke kaise draw kr skte hai.
8. Lastly humne ye seekha ki given angle ki copy kaise draw krte hai aur specific measures k angles kaise construct krte hai. We learnt how to construct angles of 60∘,30∘ and 120∘.