Linked Comprehension from CENGAGE PHYSICS (ENGLISH) WORK, POWER & ENERGY for Class 11
| Class 11 | PHYSICS |
| Chapter | WORK, POWER & ENERGY |
| CENGAGE PHYSICS (ENGLISH) | Linked Comprehension |
| Medium | English |
| Academic Year | 2023-2024 |
Question 1
Discuss whether any work is being done by each of the following agents and, if so, whether the work is positive or negative: (a) a chicken scratching the ground, (b) a person studying, (c) a crane lifting a bucket of concrete, (d) the gravitational force on the bucket in part (c), and (e) the leg muscles of a person in the act of sitting down.View SolutionQuestion 2
State the following statements as true or false.
a. The work done by a force on a body is equal to the dot product of the force and displacement of the body.
b. Instantaneously, work is not defined.
c. When several forces act on a body, the total work is the same as the work done by their resultant. View SolutionQuestion 7
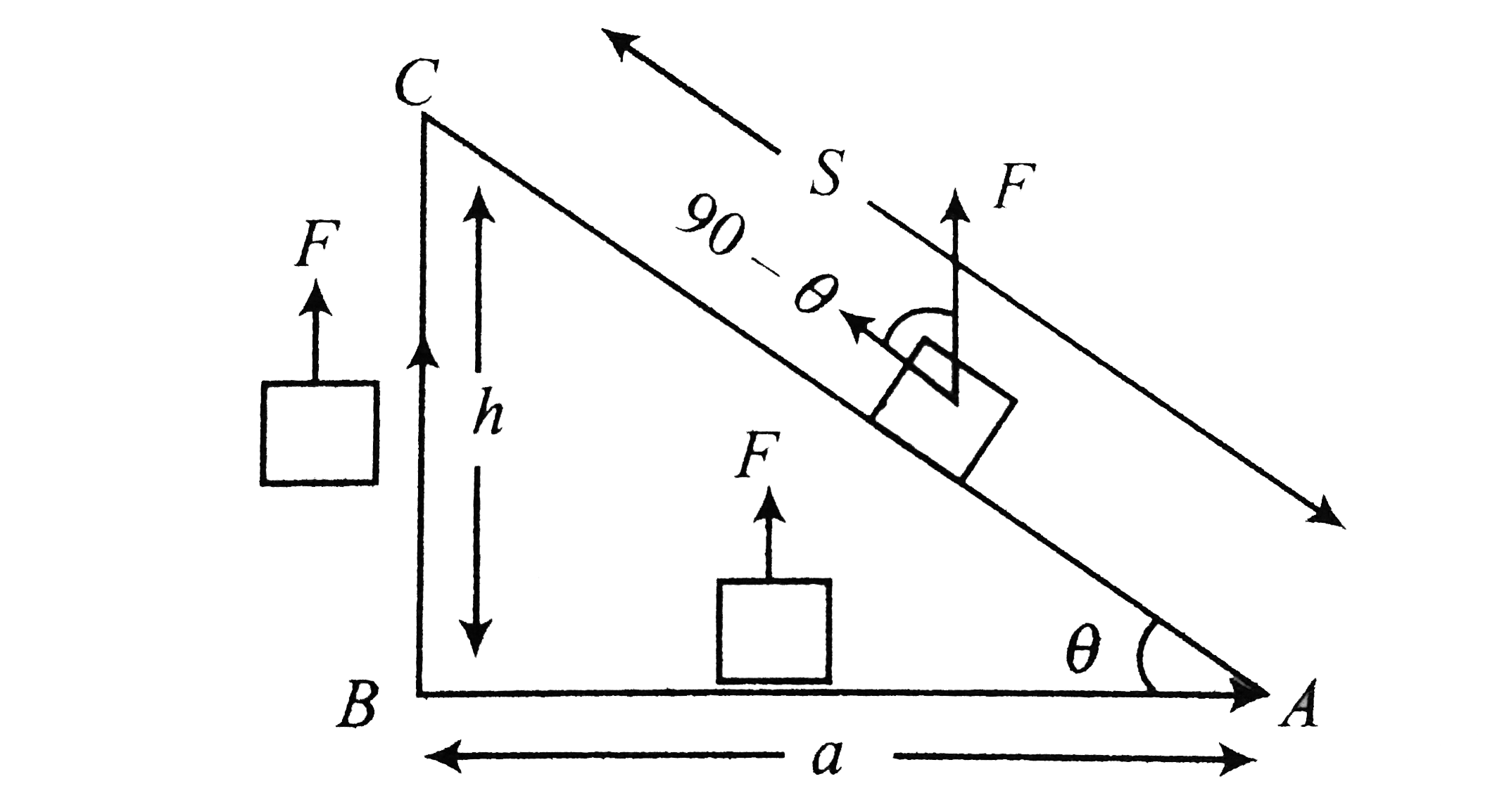
There are two inclined planes with the same vertical height, but with different angles of inclination. Two bodies of mass m each are placed at the bottom of the inclined plane. Two external forces of equal magnitude do work in taking the bodies to the top of the inclined plane. Which force does more work?View SolutionQuestion 11
A body constrained to move along the z-axis of a coordinate system is subject to a constant force F is given by
F=−ˆi+2ˆj+3ˆk N
Where, ˆi,ˆj,ˆk are unit vectors along the x−,y− and z axis of the system respectively. What is the work done by this force in moving the body a distance of 4m along the z-axis?View SolutionQuestion 15
A force →F=(3xN)ˆi+(4N)ˆj, with x in meter, acts on a particle, changing only the kinetic energy of the particle. How mcuh work is done on the particle as it moves from coordinates (2m,3m,5m) to (3m,0m,6m)? Does the speed of the particle increase, decrease, or remain the same?View SolutionQuestion 30
You are reshelving books in a library. You lift a book from the floor to the top shelf. The kinetic energy of the book on the floor was zero and the kinetic energy of the book on the top shelf is zero, so no change occurs in the kinetic energy even though you did some work in lifting the books. Is the work-kinetic energy theorem violated?View SolutionQuestion 34
A particle moves in x-y plane in figure under the influence of a friction force with magnitude 3.00N and acting in the direction opposite to the particle's displacement. Calculate the work done by the friction force on particle as it moves along the following paths: (a) path OA followed by AC (b) path OA followed by AC and the return path CO, (c) path OC followed by the return path CO, and (d) each of your three answers should be non-zero. What is the significant of this observation?
 View Solution
View SolutionQuestion 35
A single conservative force acting on a particle varies as F=(−Ax+Bx2)ˆiN, where A and B are constants and x is in meters. (a) Calculate the potential-energy function U(x) associated with this force, taking U=0 at x=0.
(b) Find the change in potential energy and the change in kinetic energy as the particle moves from x=2.00m to x=3.00m.View SolutionQuestion 40
A single conservative force acting on a particle varies as →F=(−Ax+Bx2)ˆiN, where A and B are constants and x is in meters. (a) Calculate the potential energy function U(x) associated with this force, taking U=0 at x=0. (b) Find the change in potential energy and the change in kinetic energy of the system as the particles moves from x=2.00m to x=3.00m.View SolutionQuestion 41
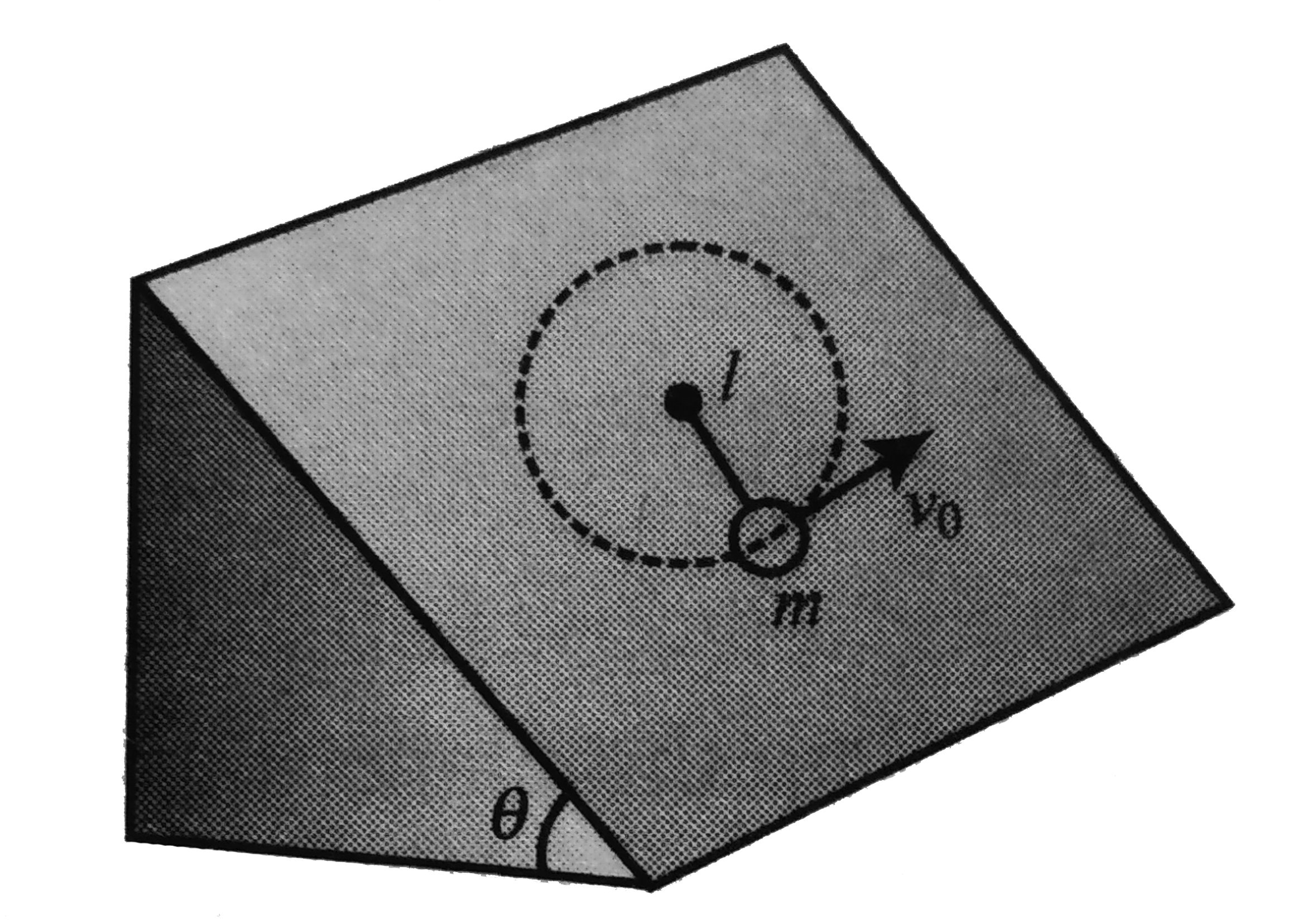
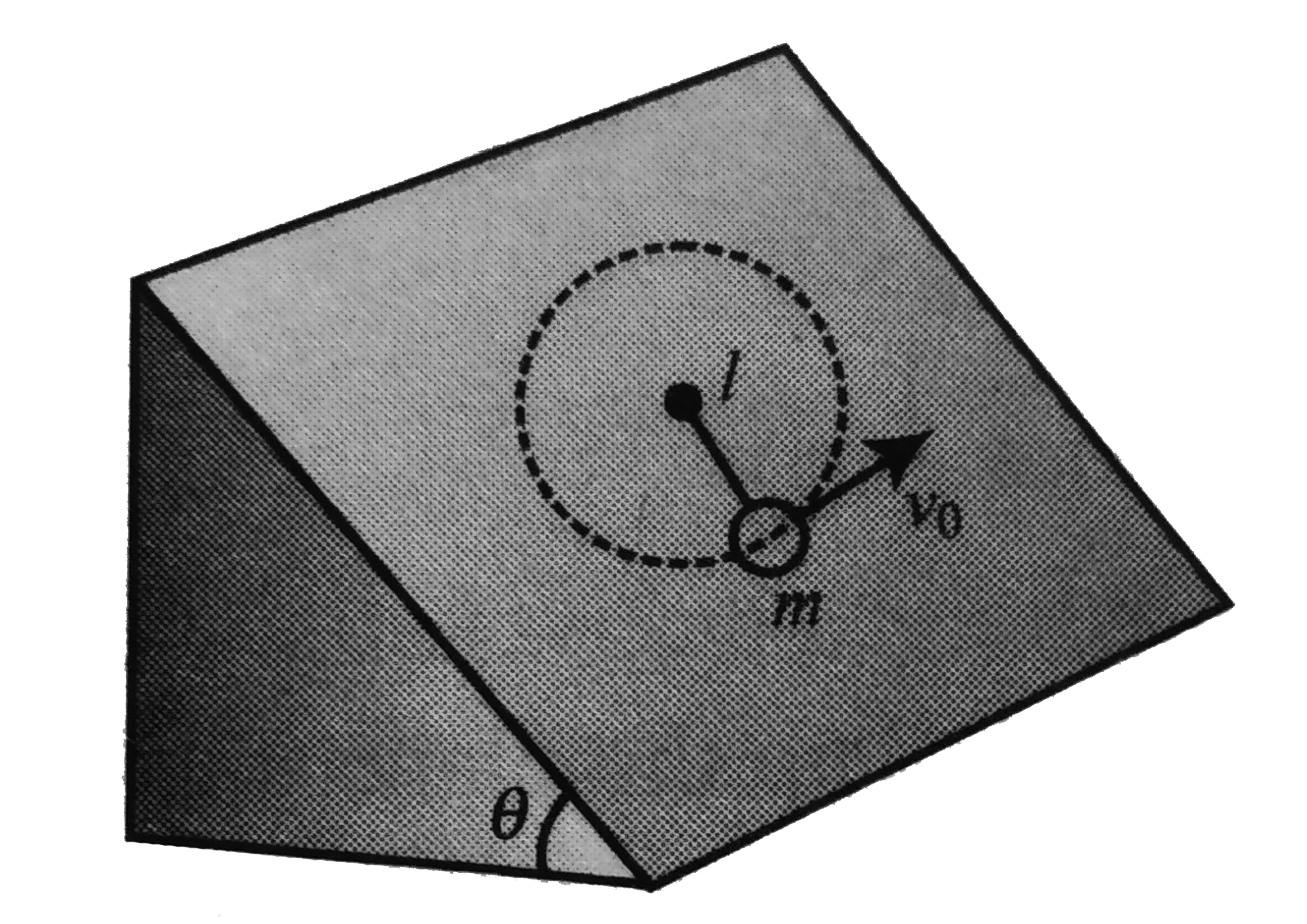
A block of mass m is placed at the bottom of a massless smooth wedge which if placed on a horizontal surface. When we push the wedge with a constant force, the block moves up the wedge. Find the work done by the external agent when the block has a speed v and is reaches the top of the wedge.
 View Solution
View SolutionQuestion 44
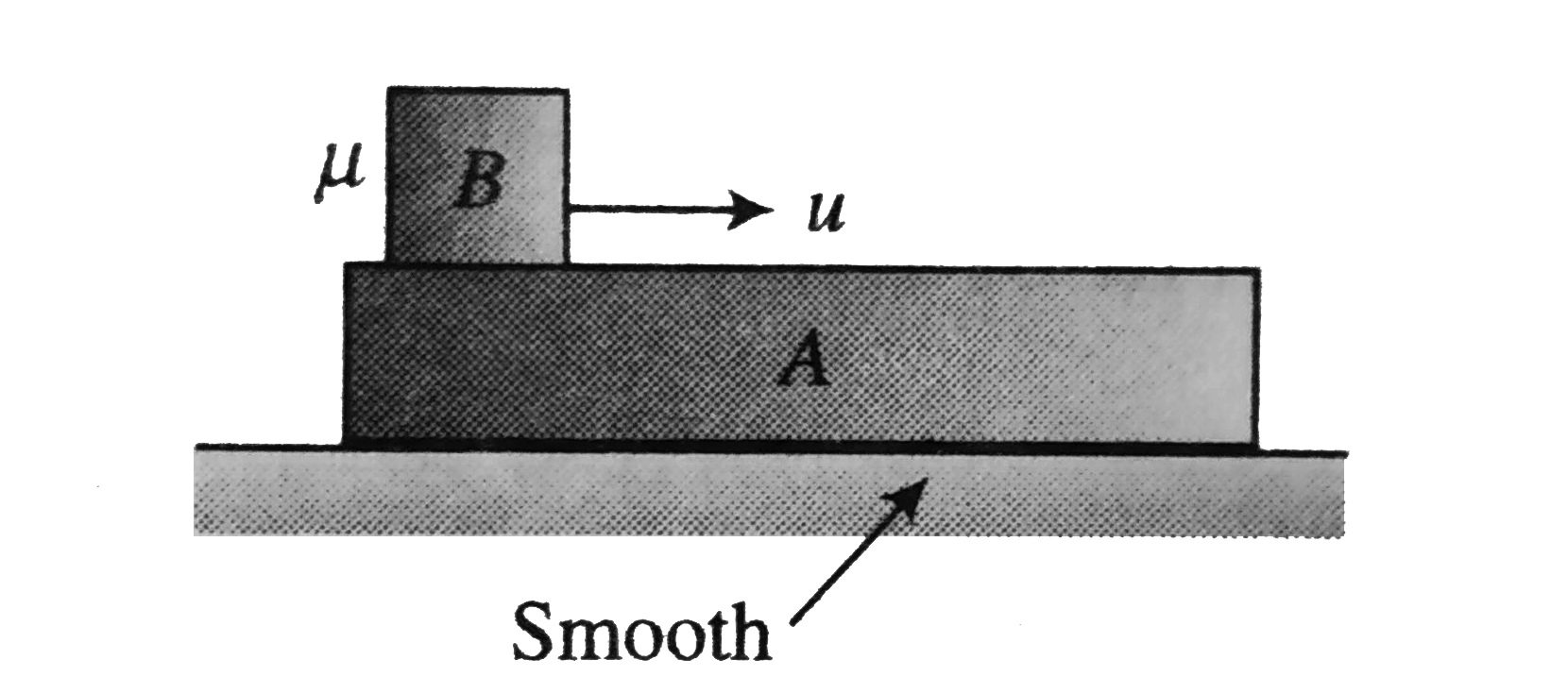
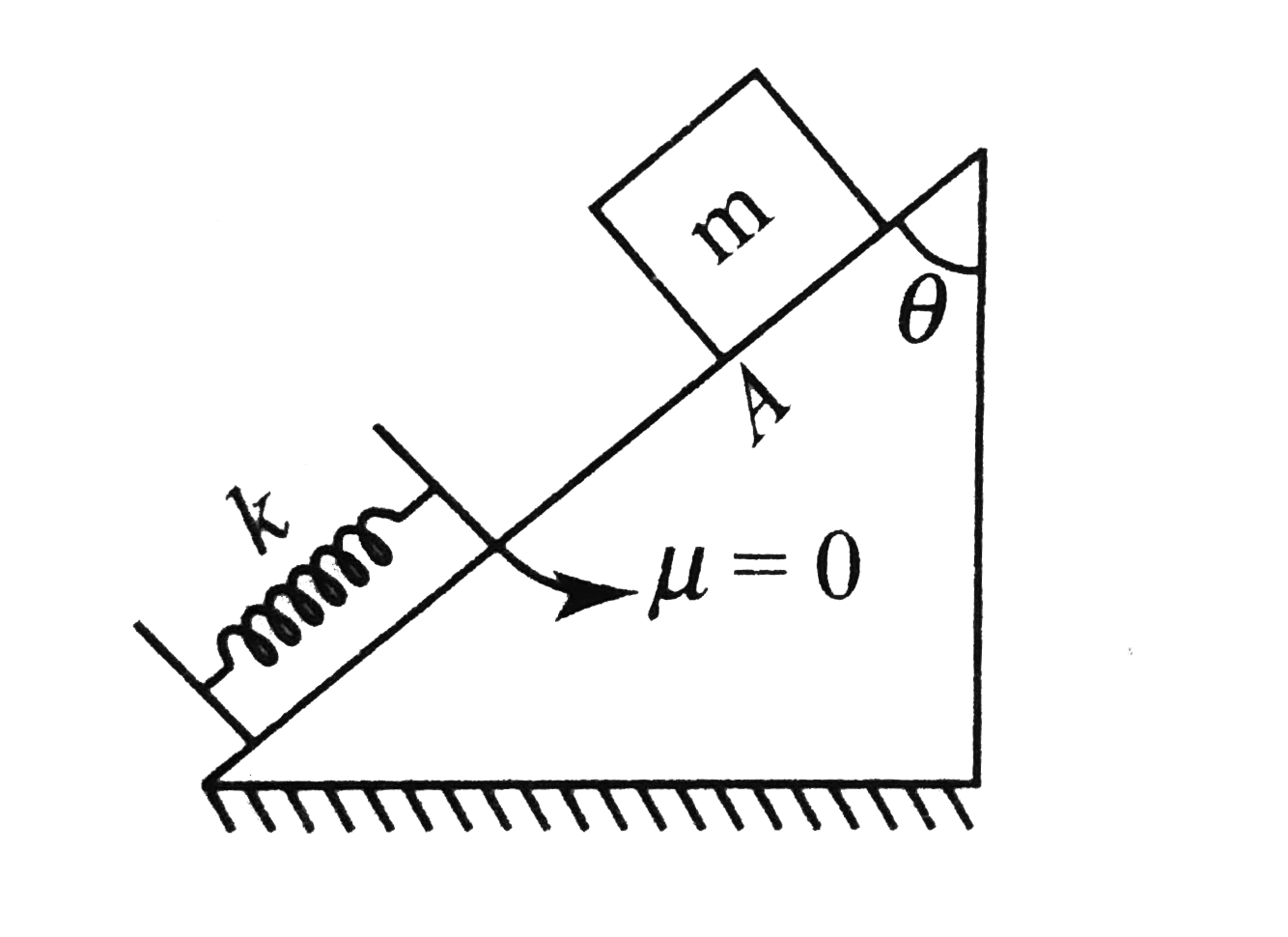
A block of mass m is connected with a rigid wall by light spring of stiffness k. Initially the spring is relaxed.

If the block is pushed with a velocity v0, it oscillates back and forth and stops. Assuming μ as the coefficient of kinetic friction between block and ground, find the work done by friction till the block stops.View SolutionQuestion 45
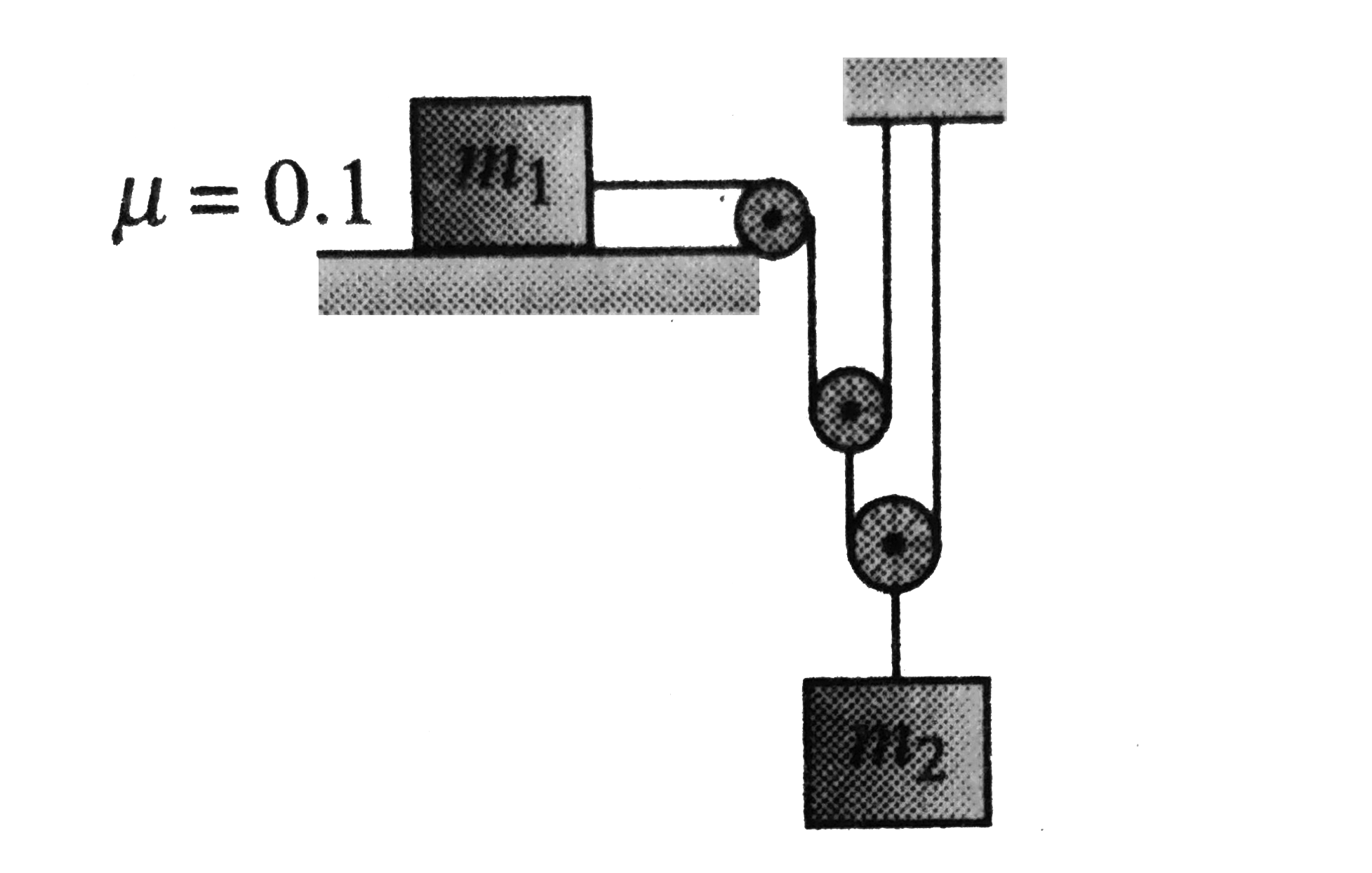
Two blocks of masses m1 and m2 inter connected by a spring of stiffness k are placed on a horizontal surface. If a constant horizontal force F acts on the block m1 it slides through a distance x whereas m2 remains stationary. If the coefficient of friction between all contacting surfaces is μ, find the speed of the block m1 as the function x.
 View Solution
View SolutionQuestion 47
A spring block system is placed on a rough horizontal surface having coefficient of friciton μ. The spring is given initial elongation 3μmg/k (where m=mass of block and k=spring constant) and the block is released from rest. For the subsequent motion, find
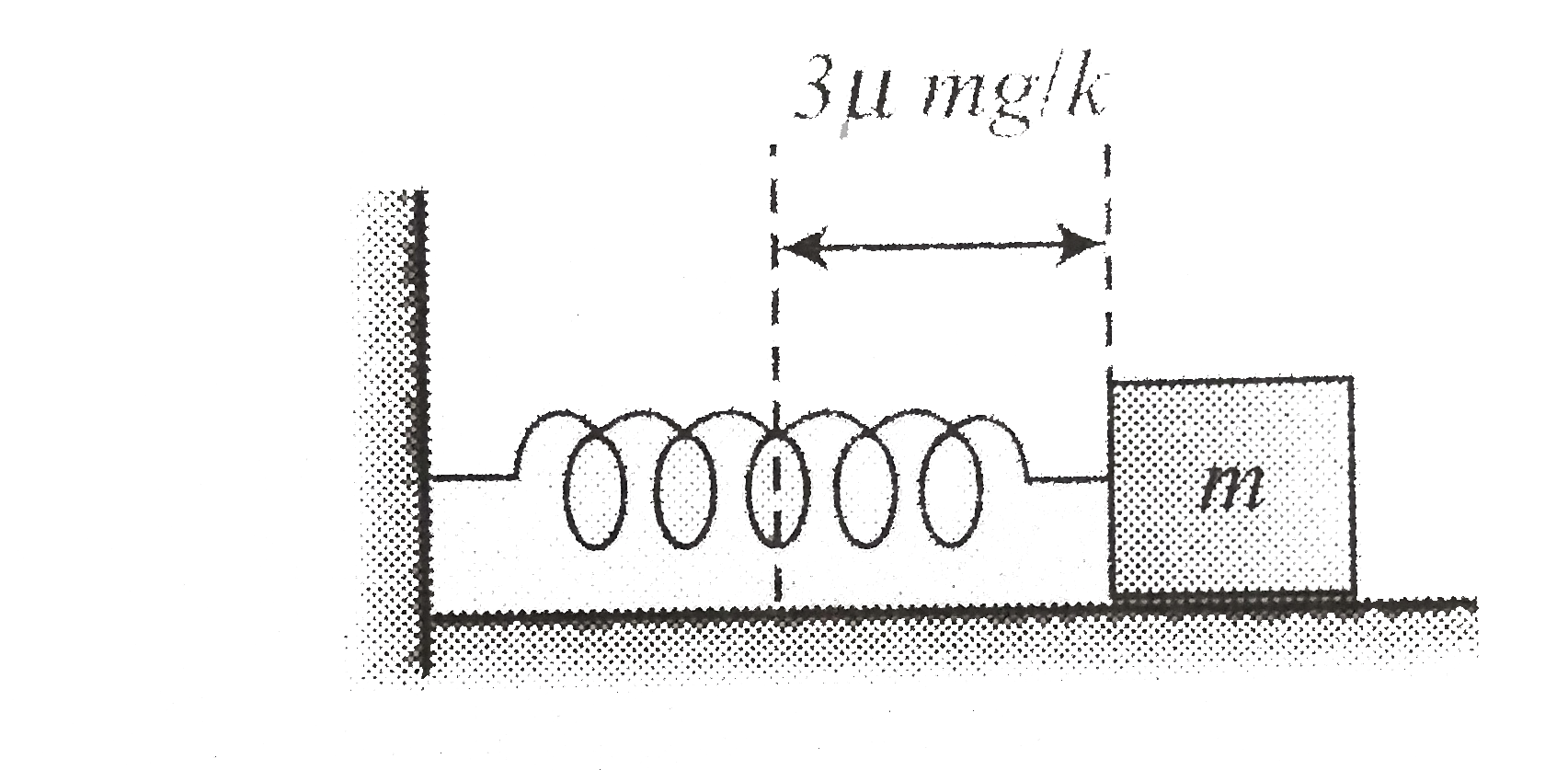
a. Initial acceleration of block
b. Maximum compression in spring
c. Maximum speed of the blockView SolutionQuestion 50
A uniform board of length L is sliding along a smooth (frictionless) horizontal plane as in figure. The board then slides across the boundary with a rough horizontal surface. The coefficient of kinetic friction between the board and the second surface surface is μk

a. Find the acceleration of the board at the moment its front end has traveled a distance x beyond the boundary.
b. The board stops at the moment its back end reaches the boundary, as in figure. Find the initail speed v of the board.View SolutionQuestion 51
Figure shows a light, inextensible string attached to a cart, which can slide along a frictionless horizontal rail aligned along the x axis. The left end of the string is pulled over a pulley of negligible mass and friction and fixed at height h=3m from the ground level. The cart slides from x1=3√3m to x2=4m and during the move, tension in the string is kept constant at 50N. Find the change in kinetic energy of the cart in joules. (Use √3=1.3)
 View Solution
View SolutionQuestion 53
An elevatore is moving up with a constant velocity. Two different masses are attached to two different springs of same spring constant. Say you do two operations expanding the spring or compressing the spring by the same distance. Which operation consumes more energy: expanding the spring or compressing it?View SolutionQuestion 57
A rock of mass m is dropped to the ground from a height h. A second rock, with mass 2m, is dropped from the same height. When the second rock strikes the ground, what is its kinetic energy? (a) Twice that of the first rock, (b) four times that of the first rock, (c) same as that of the first rock, (d) half as much as that of the first rock, (e) impossible to determine. View SolutionQuestion 58
Three identical balls are thrown from the top of a building, all with the same initial speed. As shown in figure., the first ball is thrown horizontally, second above horizontal level, and third at an angle below the horizontal. Neglecting air resistance, rank the speeds of the balls at the instant each hits the ground.
 View Solution
View SolutionQuestion 62
Two objects are connected by a light string passing over a light, frictionless pulley as shown in figure. The object of mass 5.00kg is released from rest. Using the isolated system model, (a) determine the speed of the 3.00kg object just as the 5.00−kg object hits the ground, (b) find the maximum height to which the 3.00−kg object rises.
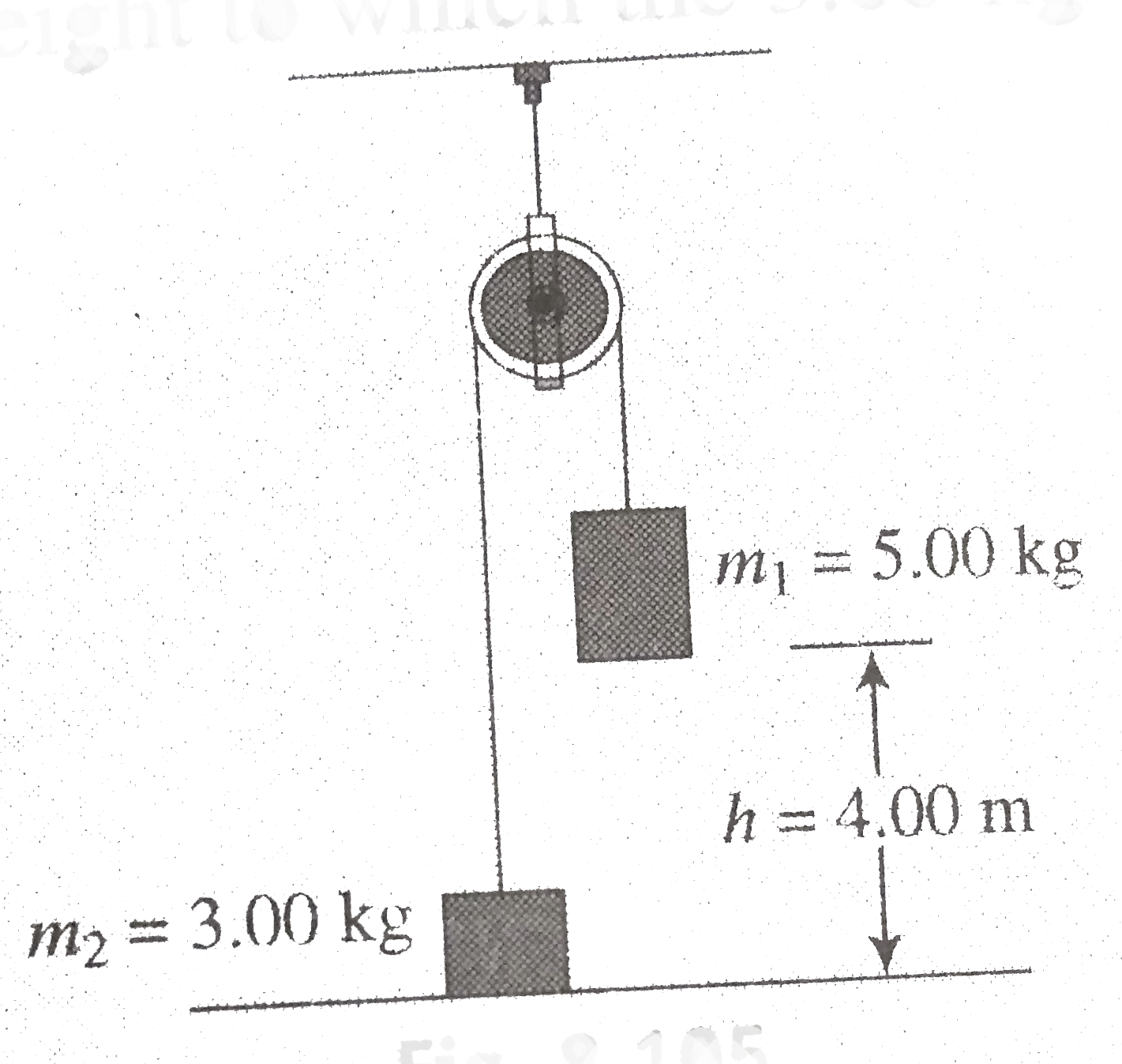 View Solution
View SolutionQuestion 63
At time t, the kinetic energy of a particle is 30.0J and the potential energy of the system to which it belongs is 10.0J. At some later time tf, the kinetic energy of the particle is 18J, what are the potential energy and the total energy at time tf? If the potential energy of the system at time t3 is 5.00J, are any non-conservative forces acting on the particle? Explain.View SolutionQuestion 67
In the figure, a block slides along a track from one level to a higher level, by moving through an intermediate valley. The track is frictionless until the block reaches the higher level. There a frictional force stops the block in a distance d. The block's initial speed υ0 in 6m/s, the height difference h is 1.1 m and the coefficient friction μ is 0.6. The value of d is (g=10m/s2)
 View Solution
View SolutionQuestion 71
A child's pogo stick(figure) stores energy in a spring with a force constant of 2.5x104Nm. At position (A) (xA=0.10m), the spring compression is a maximum and the child is momentarily at rest. At position (B) (xB=0), the spring is relaxed and the child is moving upward. At position (C), the child is again momentarily at rest at the top of the jump. The combined mass of child and pogo stick is 25kg. (a) Calculate the total energy of the child-stick-earth system if both gravitational and elastic potential energies are zero for x=0. (b) Determine xC. (c) Calculate the speed of the child at x=0. (d) Determine the value of x for which the kinetic energy of the system is a maximum. (e) Calculate the child's maximum upward speed.
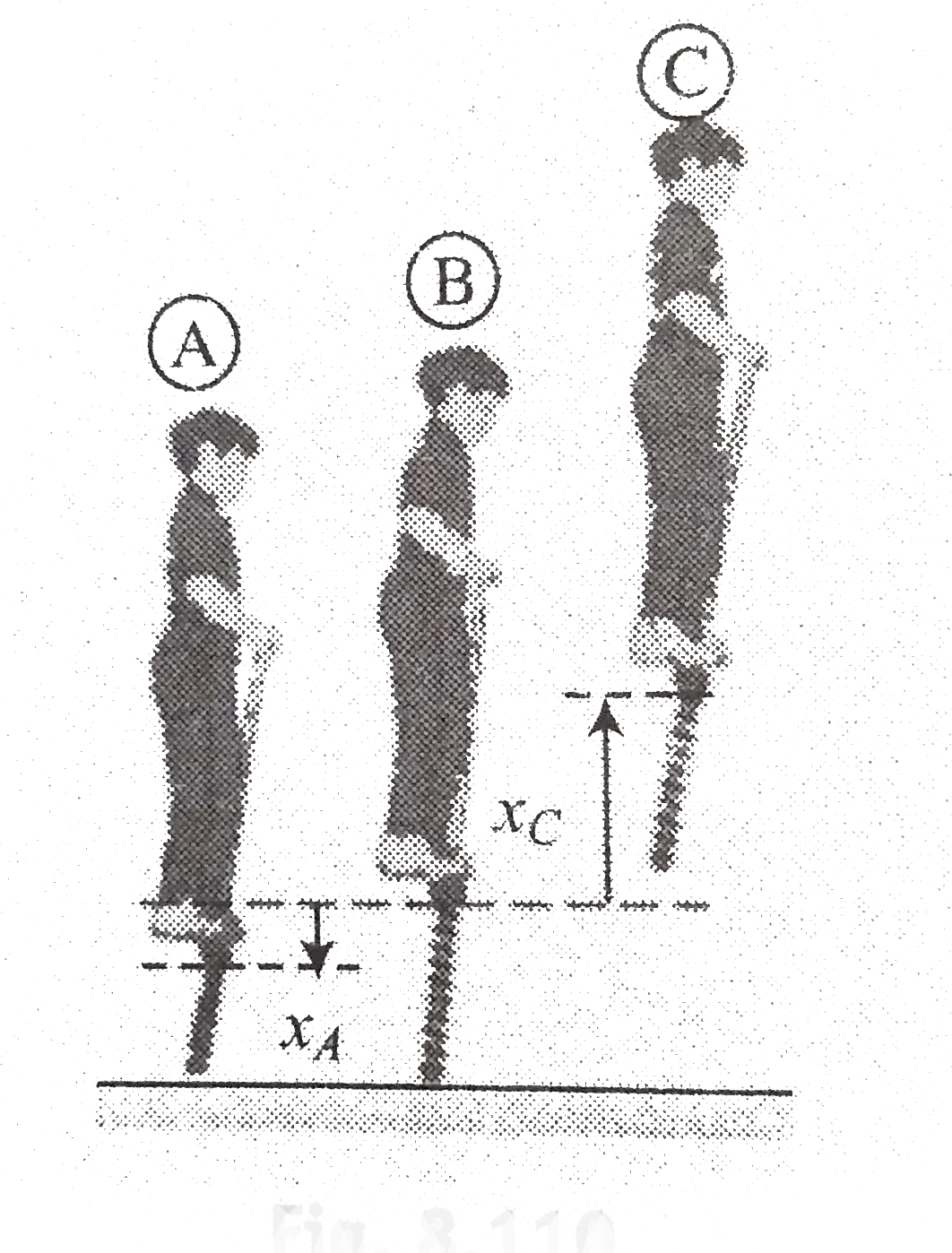 View Solution
View SolutionQuestion 72
A block of mass m is released from point (A) in figure. The track is frictionless except for the position between points (B) and (C), which has a length of dBC. The block travels down the track, hits a spring of force constant k, and compresses the spring x from its equilibrium position before coming at rest momentarily. Determine the coefficient of kinetic friction between the block and the rough surface between (B) and (C).
 View Solution
View SolutionQuestion 73
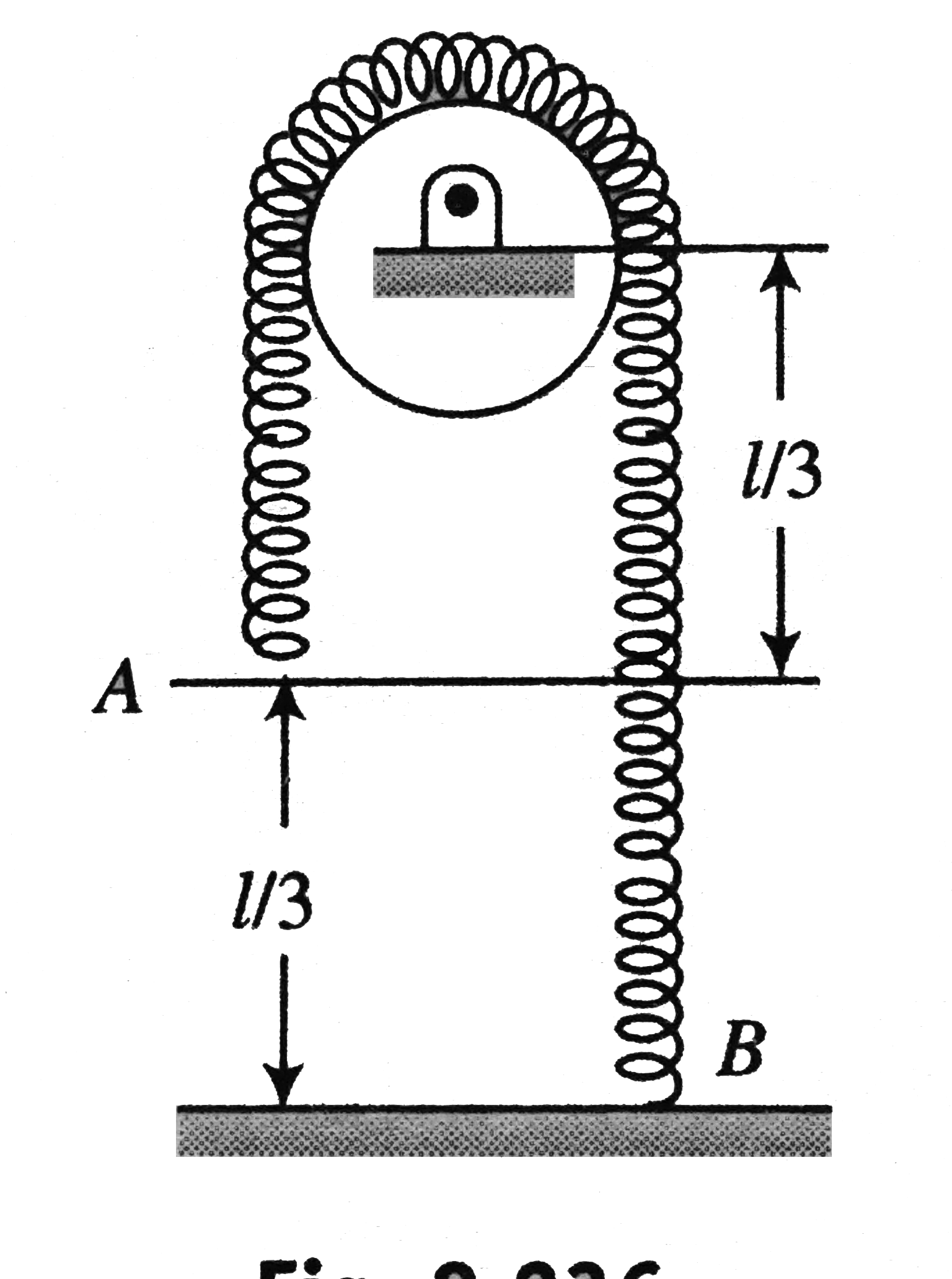
In figure, the stiffness of the spring is k and mass of the block is m. The pulley is fixed. Initially, the block m is held such that the elongation in the spring is zero and then released from rest. Find:
a. the maximum elongation in the spring.
b. the maximum speed of the block m. Neglect the mass of the spring and that of the string. Also neglect the friction.
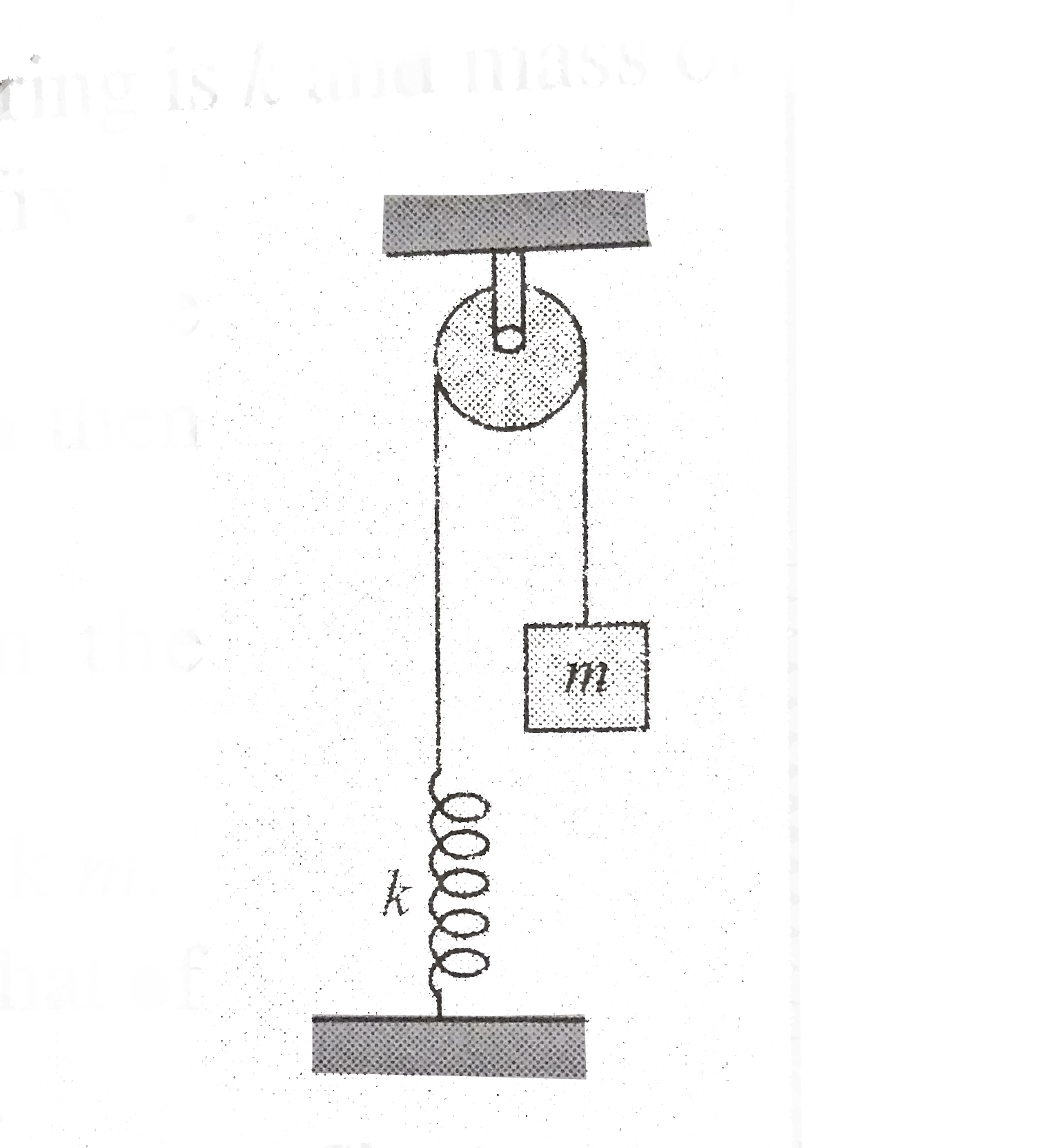 View Solution
View SolutionQuestion 76
A ring of mass m=10kg can slide through a vertical rod with friction. It is connected with a spring of force constant k=100Nm−1. The relaxed length of spring is 4m. The ring is displaced 3m as shown in the figure and released. Find velocity of ring when spring becomes horizontal.
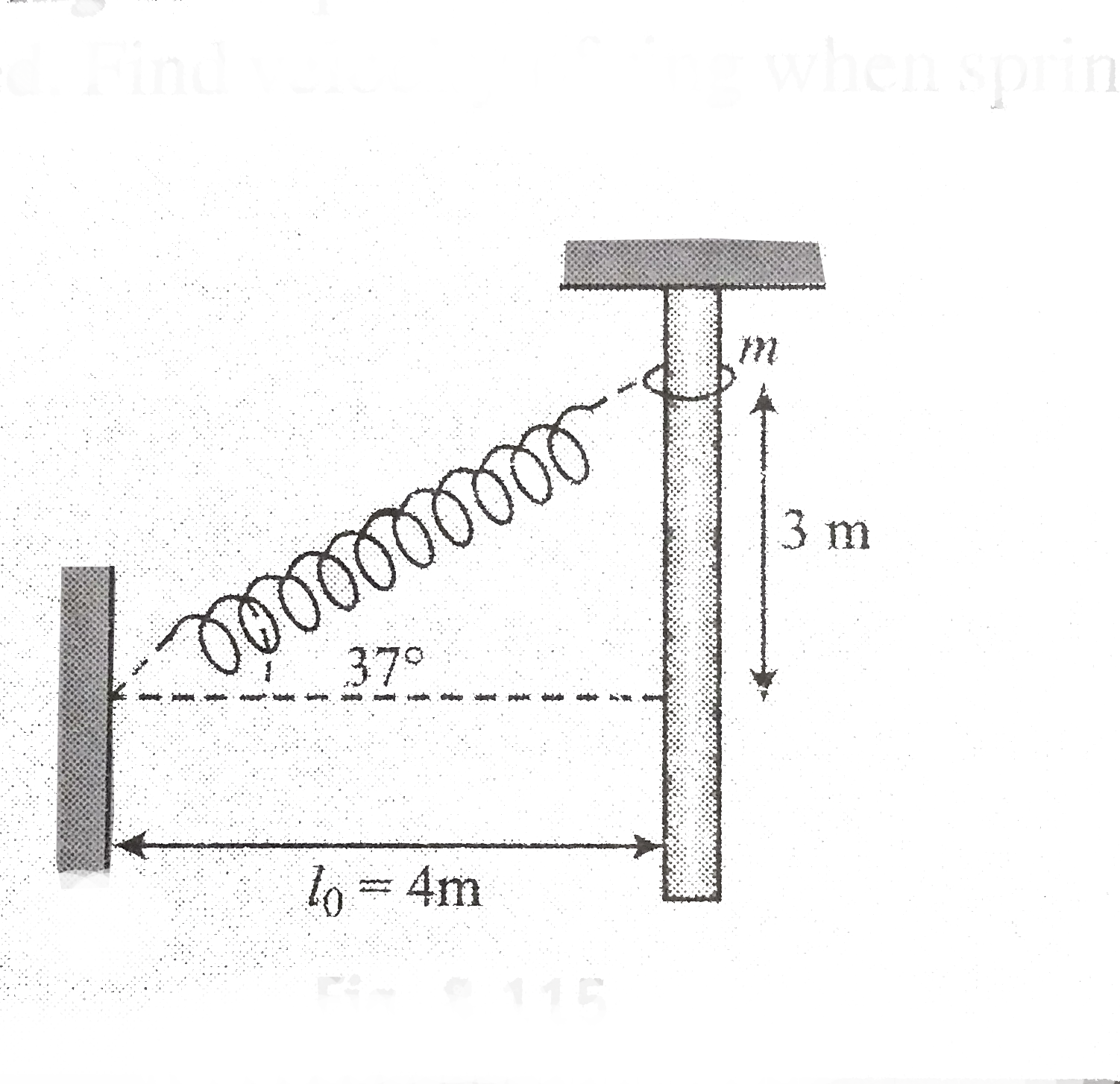 View Solution
View SolutionQuestion 77
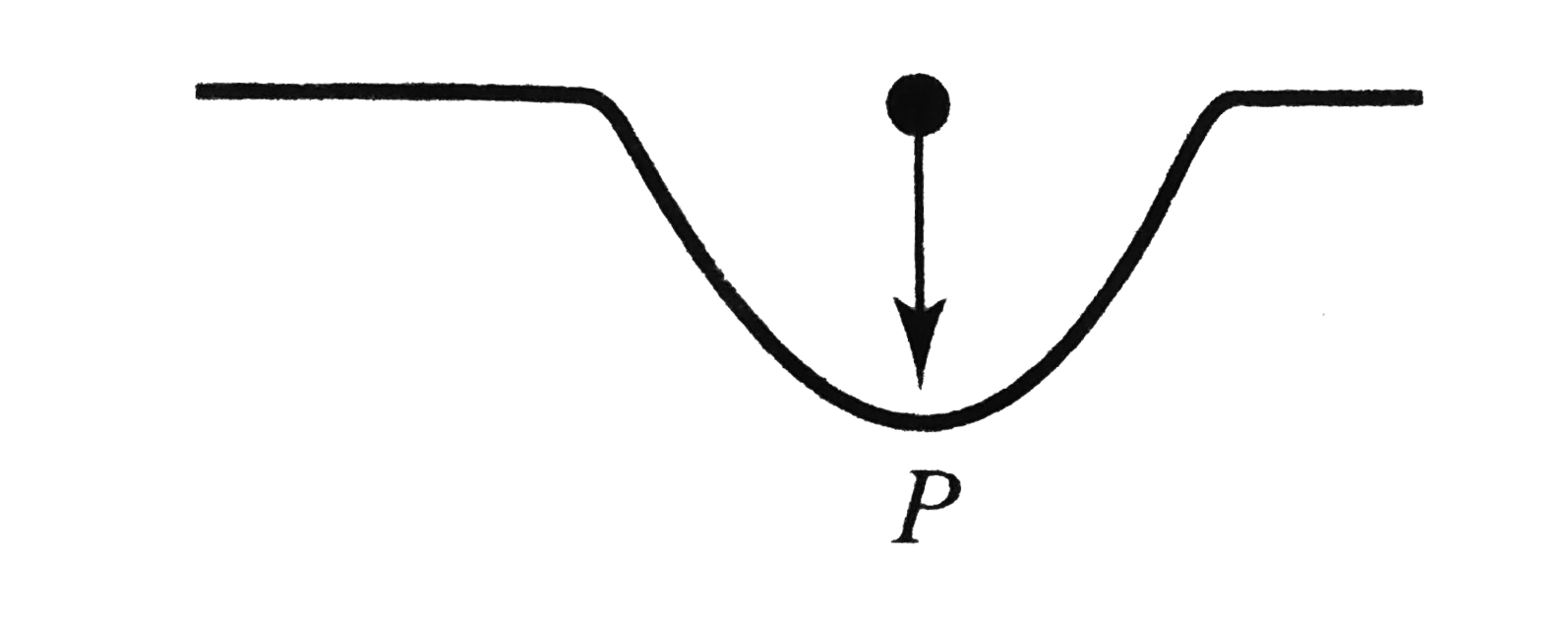
Figure shows a smooth track, a part of which is a circle of radius r. A block of mass m is pushed against a spring of spring constant k fixed at the left end and is then released. Find the initial compression of the spring so that the block presses the track with a force mg when it reaches the point P, where the radius of the track is horizontal.
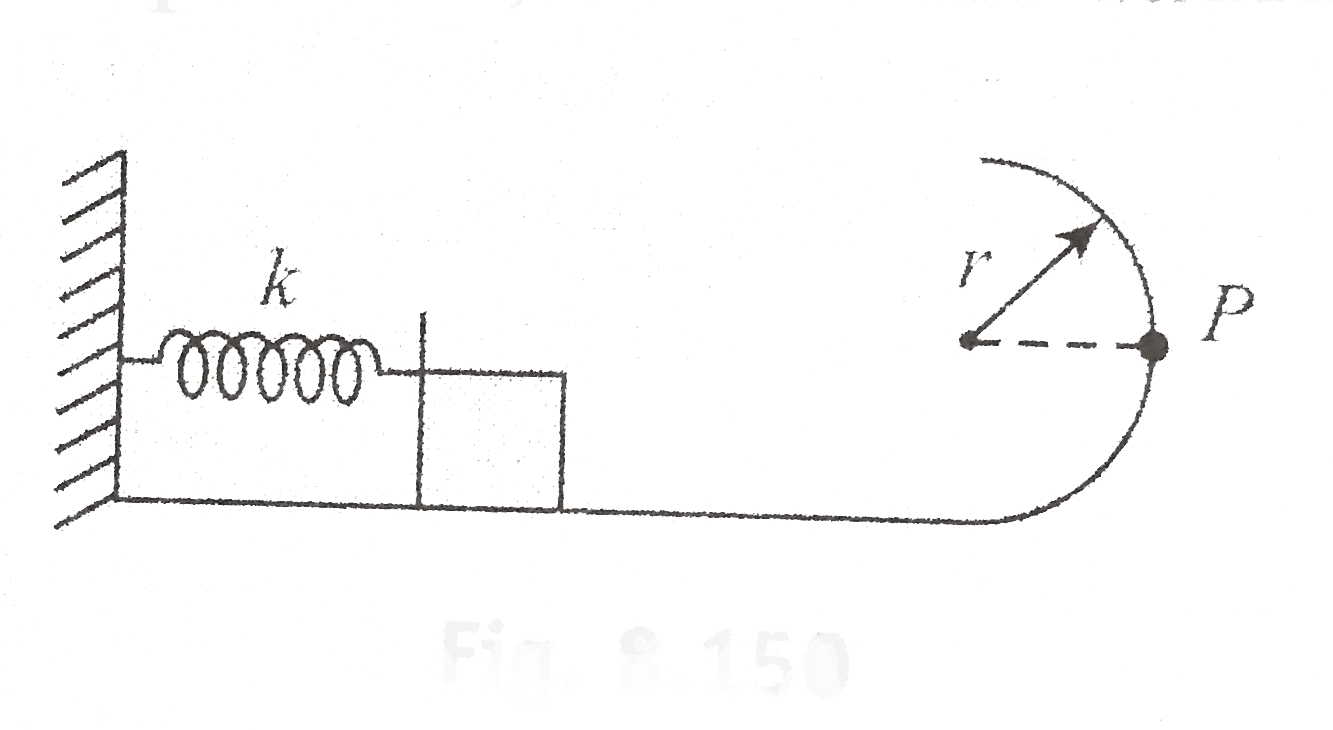 View Solution
View SolutionQuestion 78
A particle of mass m is kept on a fixed, smooth sphere of radius R at a position, where the radius through the particle makes an angle of 30 ∘ with the vertical. The particle is released from this position. (a) What is the force exerted by the sphere on the particle just after the release? (b) Find the distance traveled by the particle before it leaves contact with the sphere.View SolutionQuestion 79
A particle is suspended from a fixed point by a string of lengh 5m. It is projected from the equilibrium position with such a velocity that the string slakens after the particle has reached a height 8m above lowest point. Find the velocity of the particle, just before the string slackens.
Find also, to what to what height the particle can rise further? View SolutionQuestion 80
A heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizonally with speed √gl . Find the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string is equal to the weight of the particle. View SolutionQuestion 81
A ball is attached to a horizontal cord of length l whose other end is fixed. (a) If the ball is released, what will be its speed at the lowest point of its path? (b) A peg is located a distance h directly below the point of attachment of the cord. If h=0.75l, what will be the speed of the ball when it reaches the top of its circular path about the peg?View SolutionQuestion 82
A smooth sphere of radius R is made to translate line with a constant acceleration a=g. A particle kept on the top of the sphere is released from there at zero velocity with respect to the sphere. Find the speed of the particle with respect to the sphere as a function of angle θ as it slides down.View SolutionQuestion 87
A simple pendulum of length l and mass m free to oscillate in vertical plane. A nail is located at a distance d=l−a vertically below the point of suspension of a simple pendulum. The pendulum bob is released from the position where the string makes an angle of 90∘ from vertical. Discuss the motion of the bob if (a) l=2a and (b) l=2.5a.View SolutionQuestion 90
A cabin is moving upwards with a constant acceleration g. A boy standing in the cabin wants to whirl a particle of mass m in a vertical circle of radius l. (Mass is attached to an ideal string.) Calculate minimum velocity which should be provided at lowermost point (w.r.t cabin) so that particle can just complete the circle.
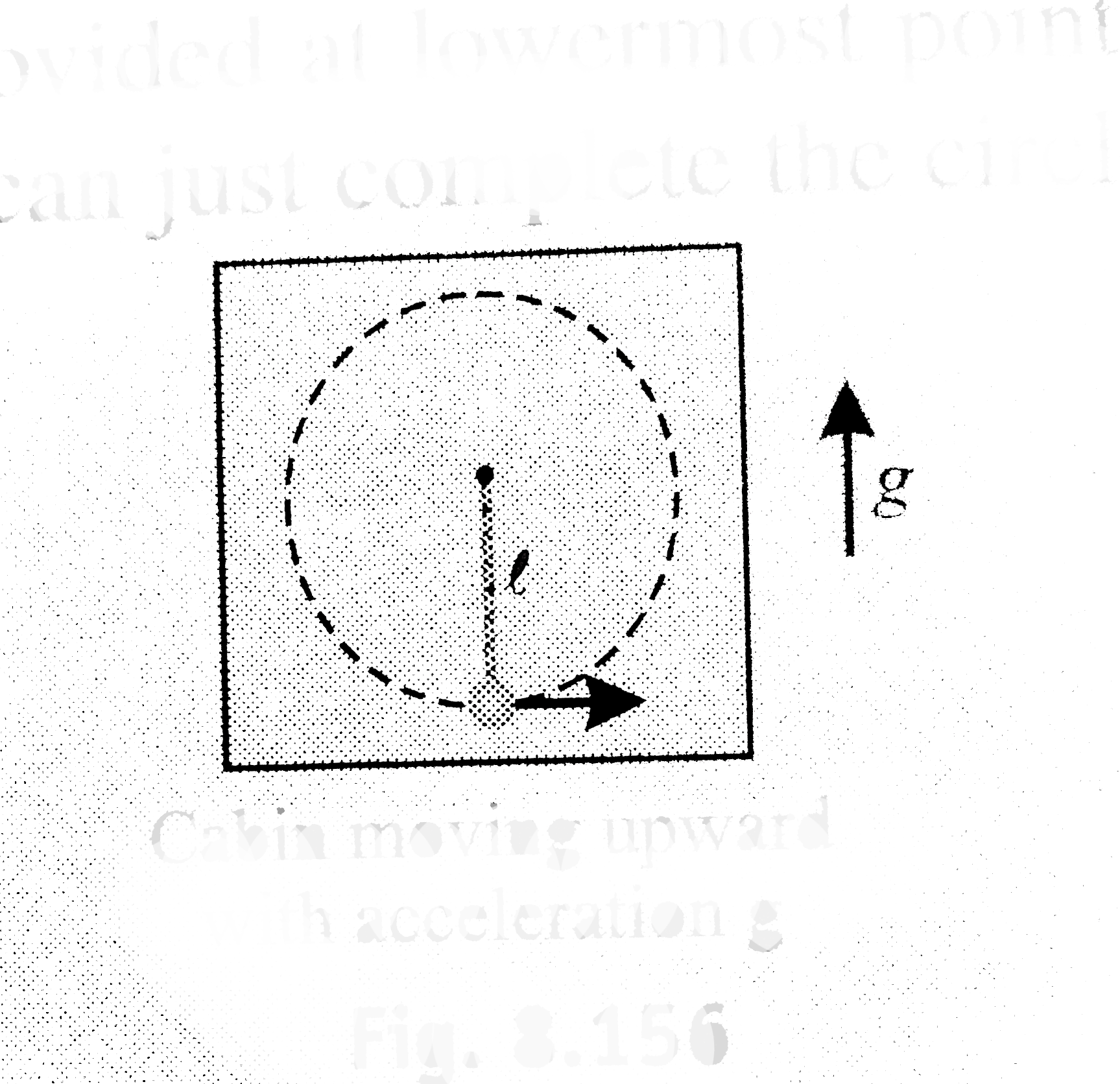 View Solution
View SolutionQuestion 96
The blades of a windmill sweep out a circle of area A. (a) If the wind flows at a velocity v perpendicular to the circle, what is the mass of the air passing through in time t? (b) What is the kinetic energy of the air? (c) Assume that the windmill converts 25% of the wind's energy into electrical energy, and that A=30m2, v=36kmh−1 and the density of air is 1.2kgm−3, what is the electrical power produced?View SolutionQuestion 101
A 90−kg man runs up an escalator while it is not in operation in 10s. What is the average power developed by the man. Suppose the escalator is running so that the escalator steps move at a speed of 0.5m−1. What is then the power developed by the man as seen by the ground reference if he moves at the same speed relative to the escalator steps as he did when the escalator is not in operation?
 View Solution
View SolutionQuestion 108
In figure, the pulley shown is smooth. The spring and the string are light. Block B slides down from the top along the fixed rough wedge of inclination θ. Assuming that the block reaches the end of the wedge, find the speed of the block at the end. Take the coefficient of friction between the block and the wedge to be μ and that the spring was relaxed when the block was released from the top of the wedge.
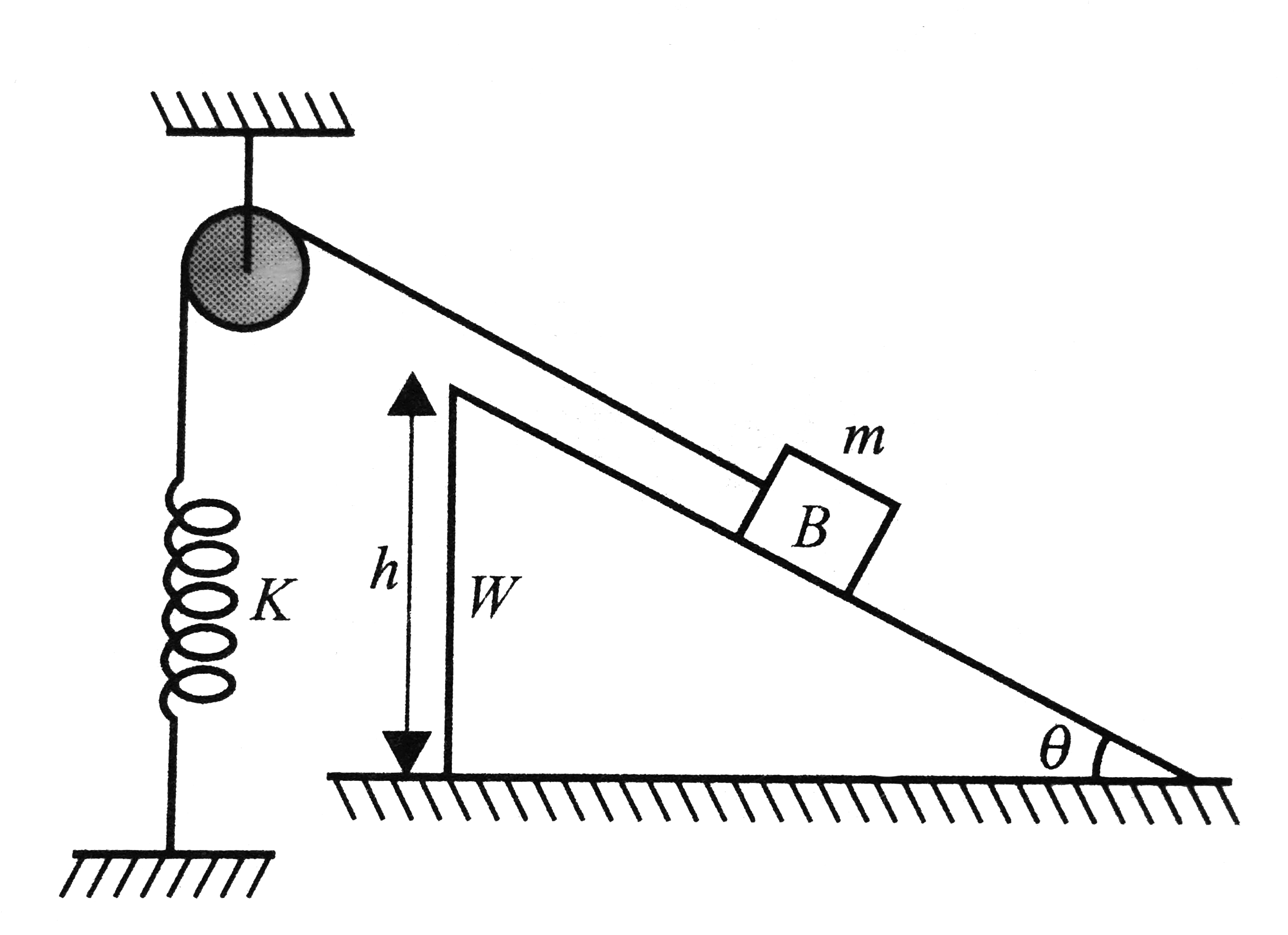 View Solution
View SolutionQuestion 110
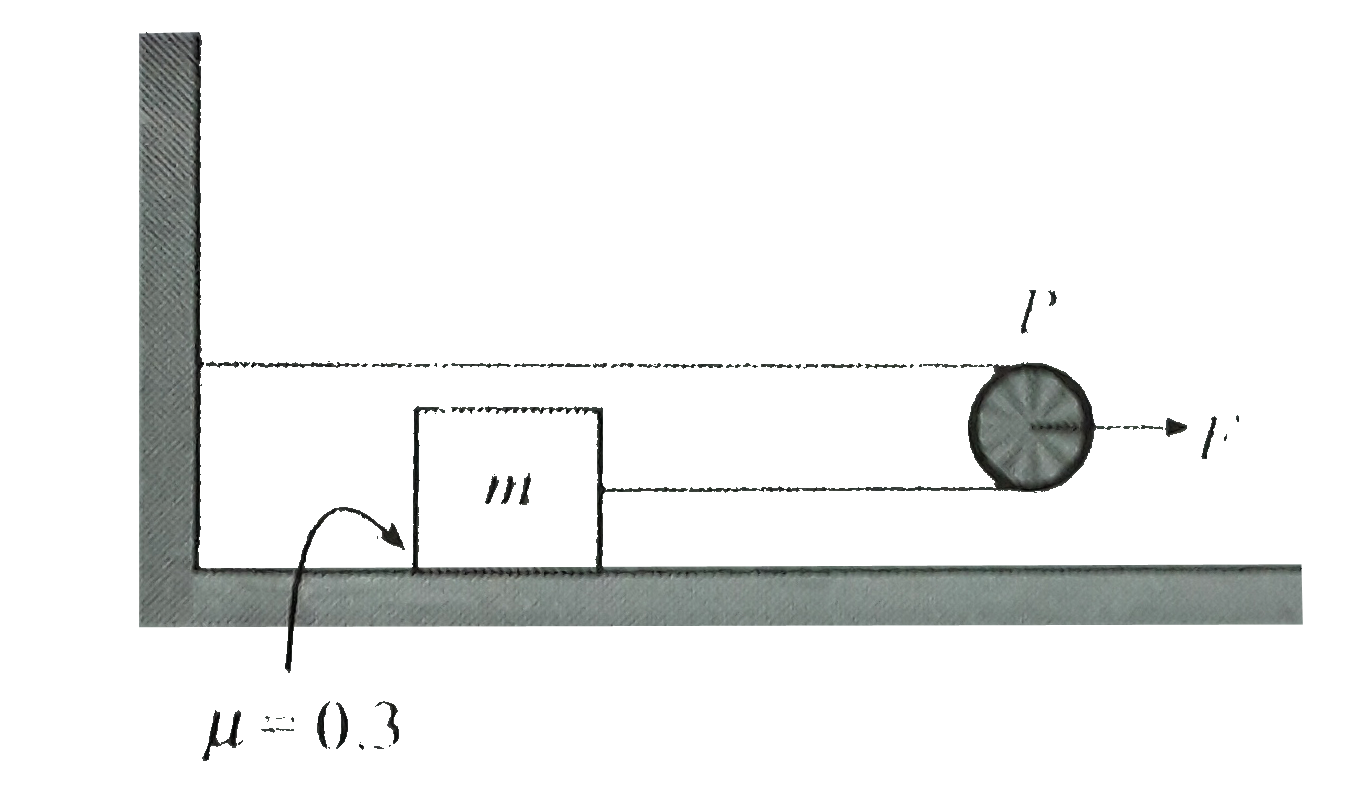
A small block of mass 20kg rests on a bigger block of mass 30kg, which lies on a smooth horizontal plane. Initially the whole system is at rest. The coefficient of friction between the blocks is 0.5. The horizontal force F=50N is applied on the lower block.
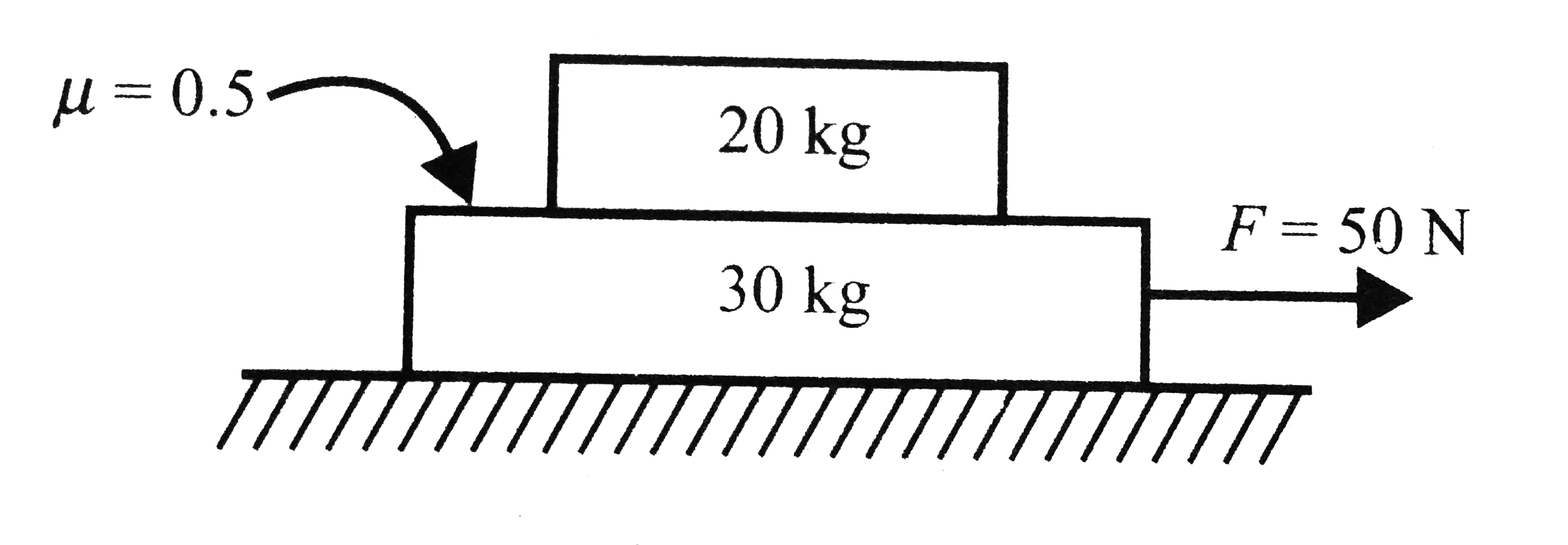
a. Find the work done by fricitonal force on upper block and on the lower block in t=2s.
b. Is the magnitude of work done by the frictional force on upper and lower blocks same?
c. Is the work done by the frictional force on the upper block converted to heat or mechanical energy or both?View SolutionQuestion 111
A small block of mass m=1kg is attached with one end of the spring of force constant K=110Nm−1. Other end of the spring is fixed to a rough plane having coefficient of friction μ=0.2. The spring is kept in its natural length by an inextensible thread ties between its ends as shown in figure. If the thread is burnt, calculate the elongation of the spring when the block attains static equilibrium position.
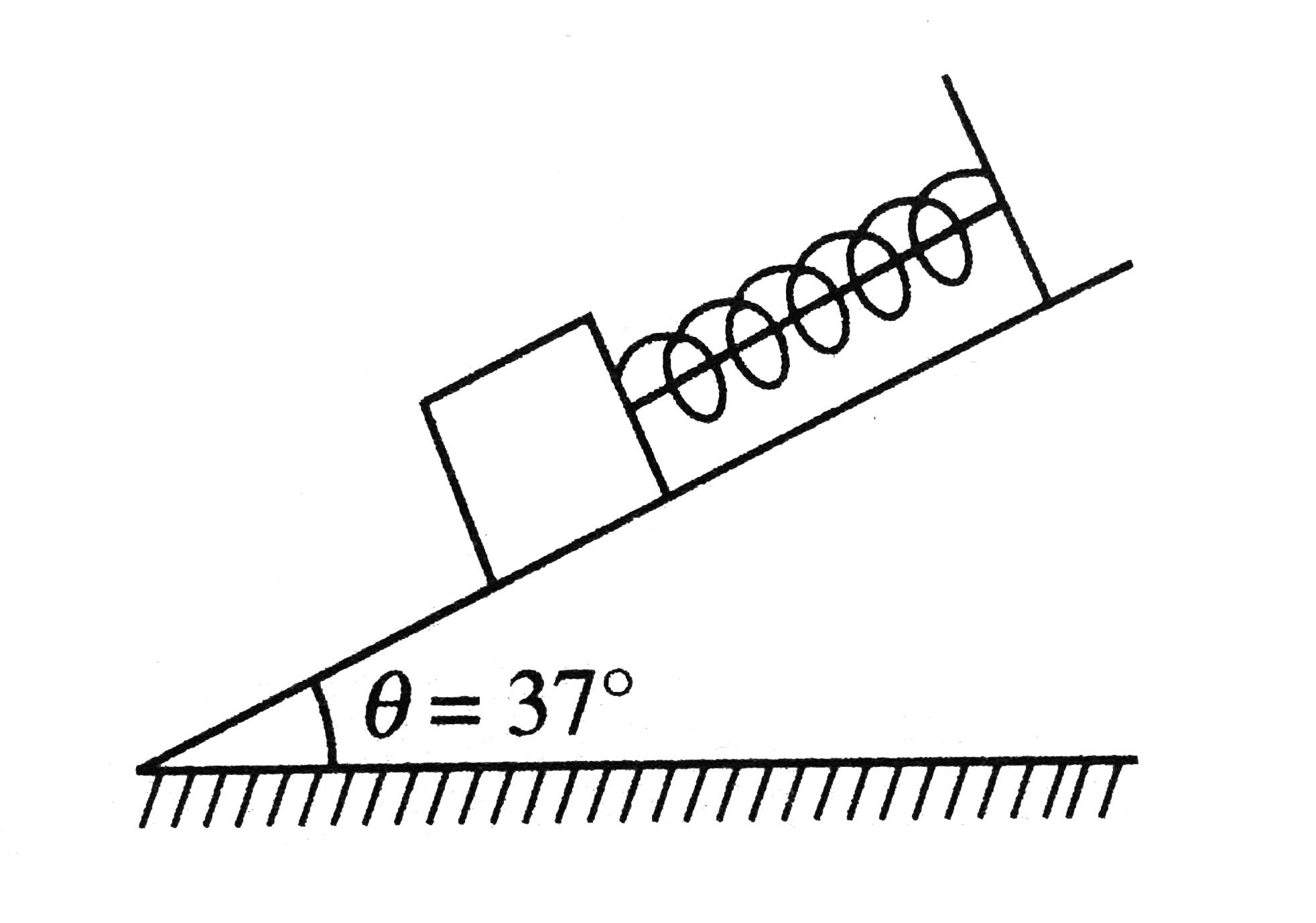 View Solution
View SolutionQuestion 112
Two identical beads, each of m=100g, are connected by an inextensible massless string, which can slide along the two arms AC and BC of a rigid smooth wire frame in a vertical plane. If the system is released from rest, the kinetic energy of the first bead when the second bead has moved down by a distance of 0.1m is ×x10−3J. Find the value of x(g=10ms−2) (shown situation is after movement of 0.1m).
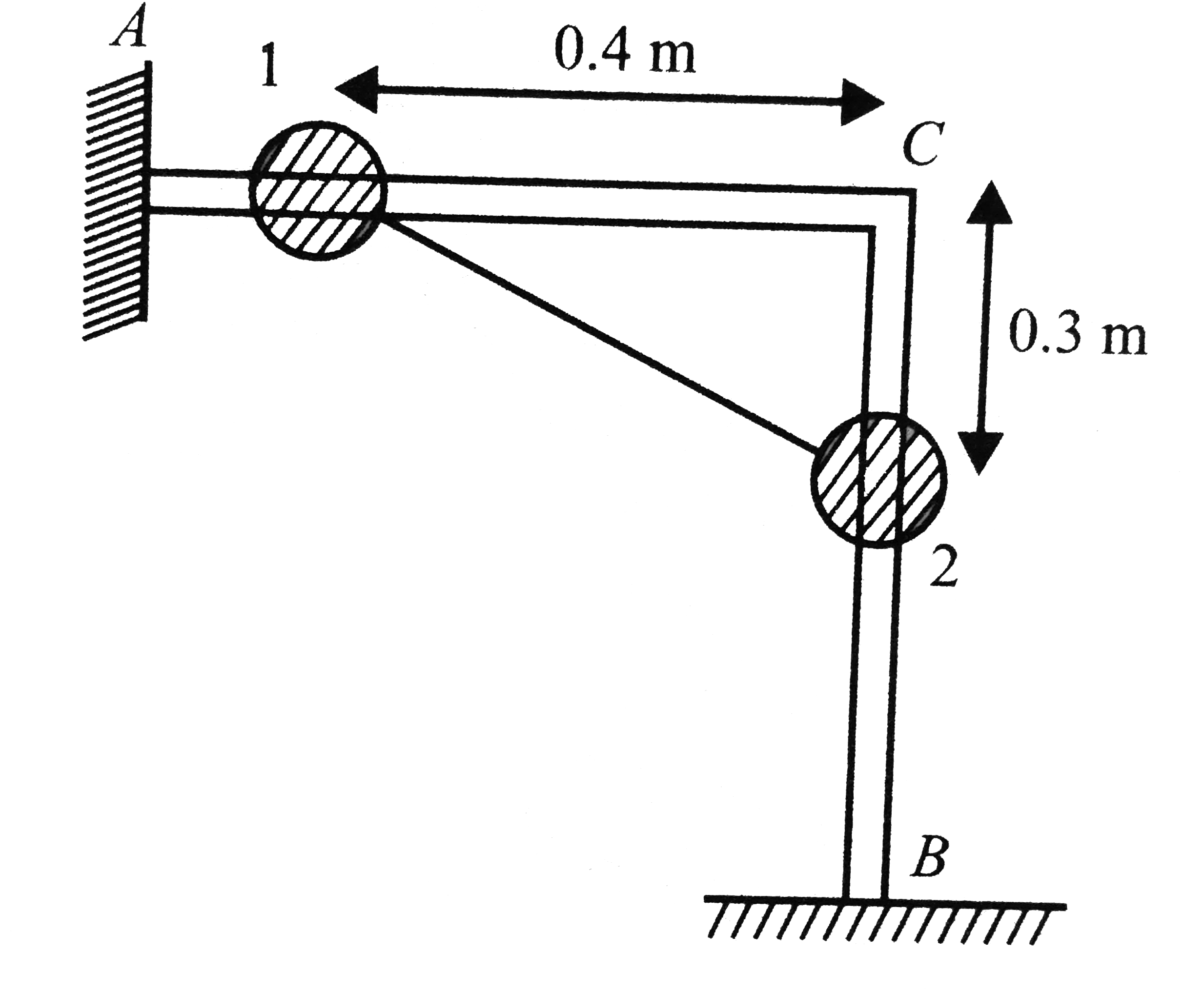 View Solution
View SolutionQuestion 113
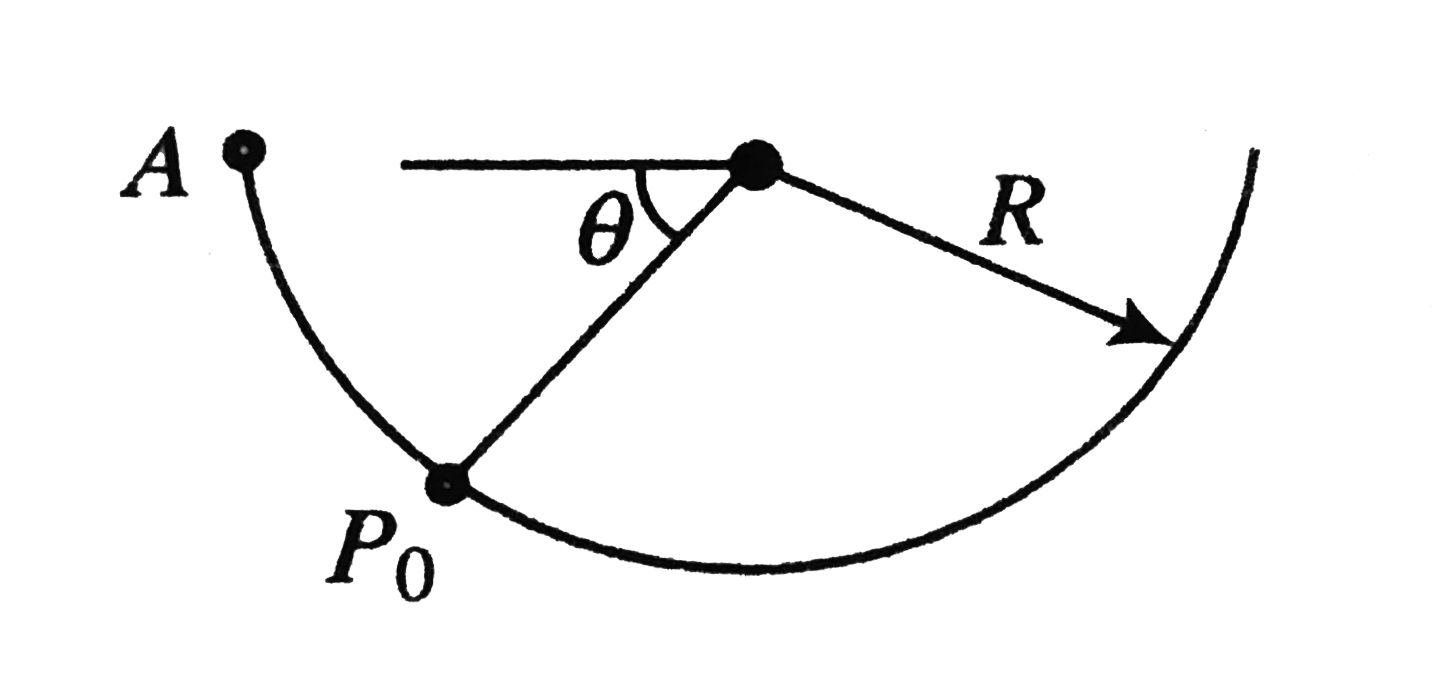
AB is a quarter of smooth circular track of radius R=6m. A particle P of mass 0.5kg moves along the track from A to B under the action of the following forces.
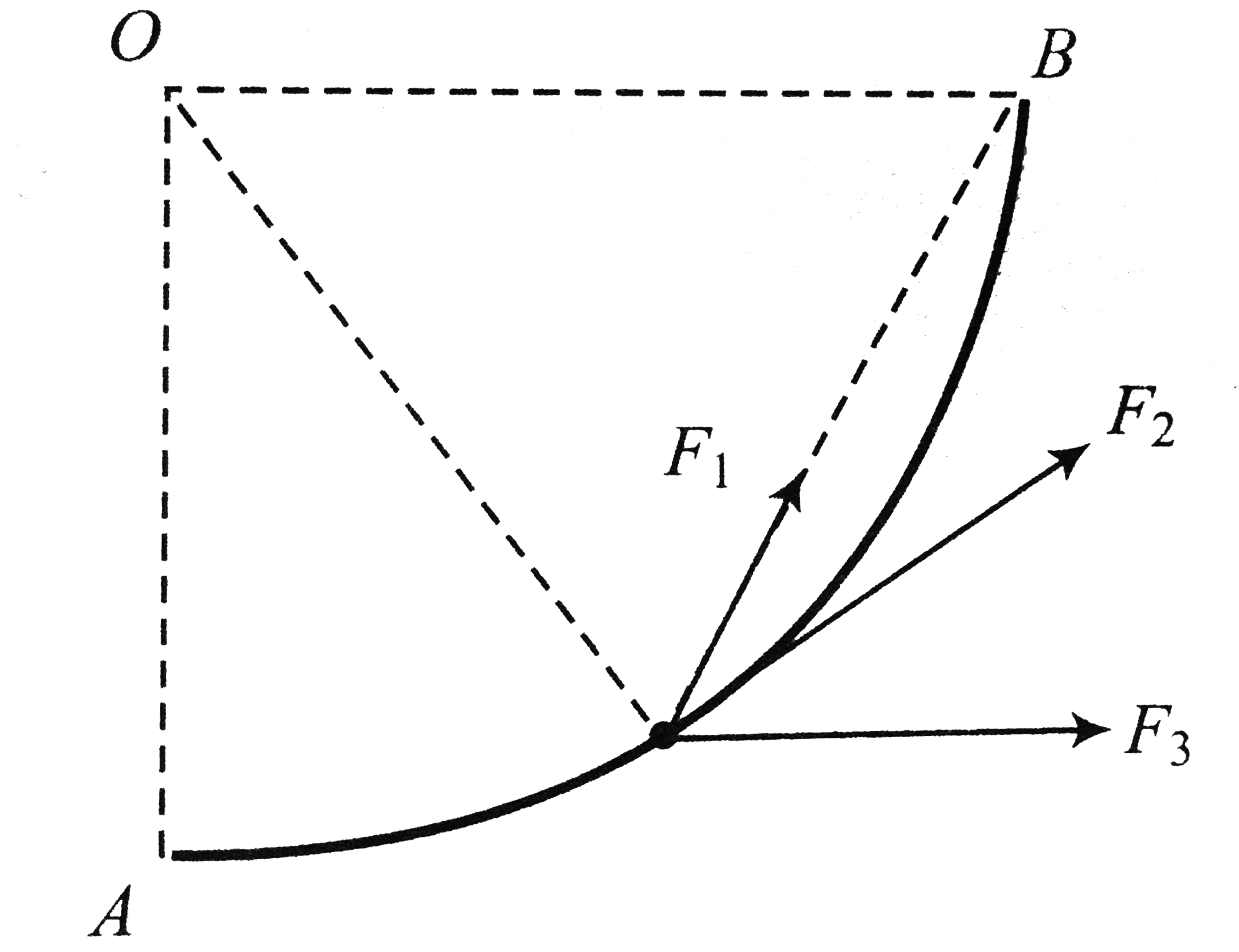
a. A force F1 directed always towards the point B, its magnitude is constant and is equal to 20N.
b. A force F2 directed along the instantaneous tangent to the circular track, its magnitude is (15−10S)N, where S is the distance travelled in metre.
c. A horizontal force of magnitude 30N.
Find the work done by forces mentioned in (a), (b) and (c) View SolutionQuestion 116
A block of mass m is dropped onto a spring of constant k from a height h. The second end of the spring is attached to a second block of mass M as shown in figure. Find the minimum value of h so that the block M bounces off the ground. If the block of mass m sticks to the spring immediately after it comes into contact with it.
 View Solution
View SolutionQuestion 117
A particle of mass m attached with a massless spring natural length l and stiffness k is released from rest from the horizontal position of the relaxed spring. When the particle passes through its lowest point, the maximum length of the spring becomes 2l. Find the:
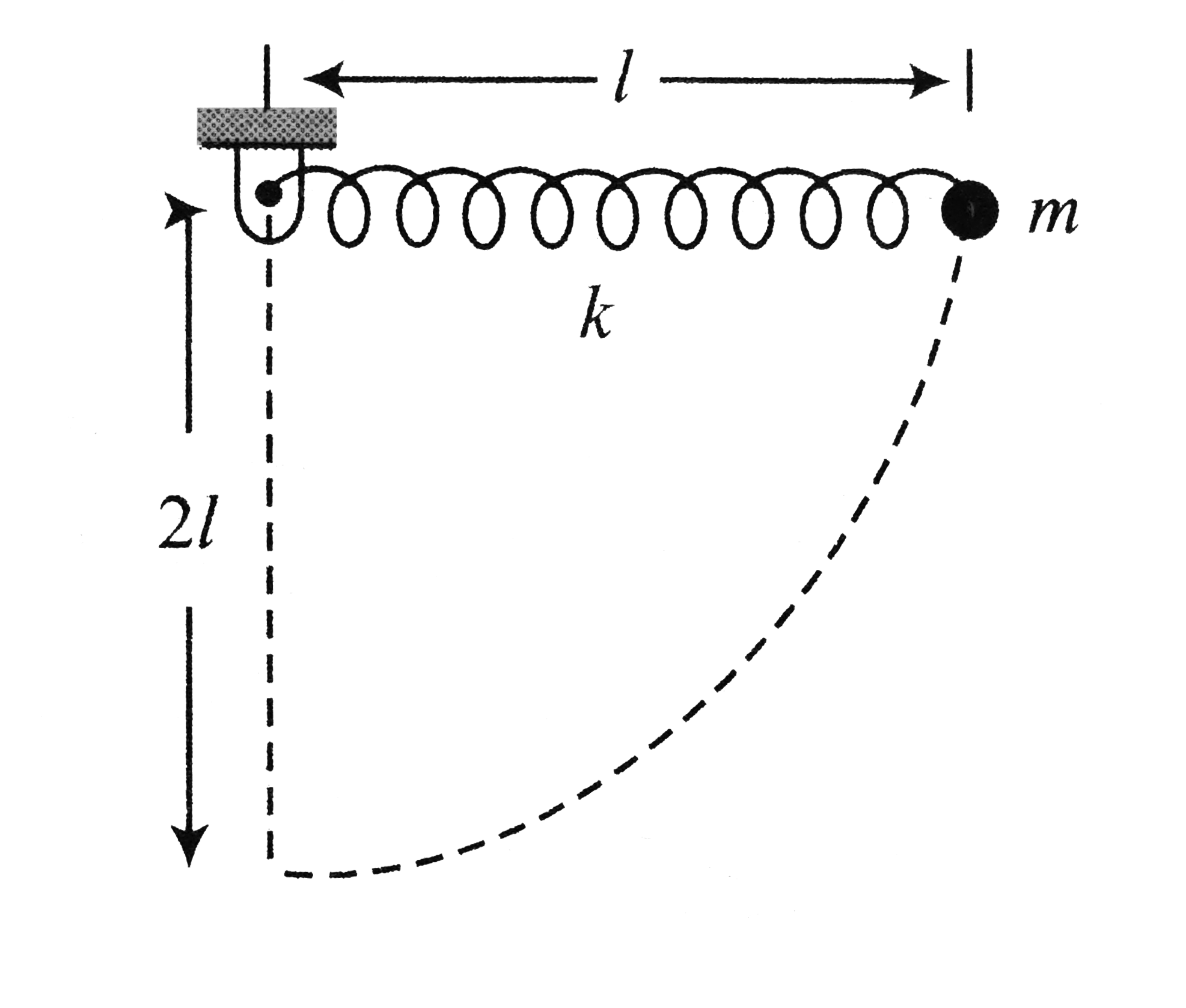
a. speed of the particle at its lowest point.
b. acceleration of the particle at its lowest position.View SolutionQuestion 118
Two blocks having masses 8kg and 16kg are connected to the two ends of a light spring. The system is placed on a smooth horizontal floor. An inextensible string also connects B with ceiling as shown in the figure at the final moment. Initially the spring has its natural length. A constant horizontal force F is applied to the heavier block as shown. What is the maximum possible value of F so the lighter block doesn't loose contact with ground?
 View Solution
View SolutionQuestion 119
a. A 2−kg situated on a smooth fixed incline is connected to a spring of negligible mass, with spring constant k=100Nm−1, via a frictionless pulley. The block is released from rest when the spring is unstretched. How far does the block moves down the incline before coming (momentarily) to rest? What is its acceleration at its lower point?
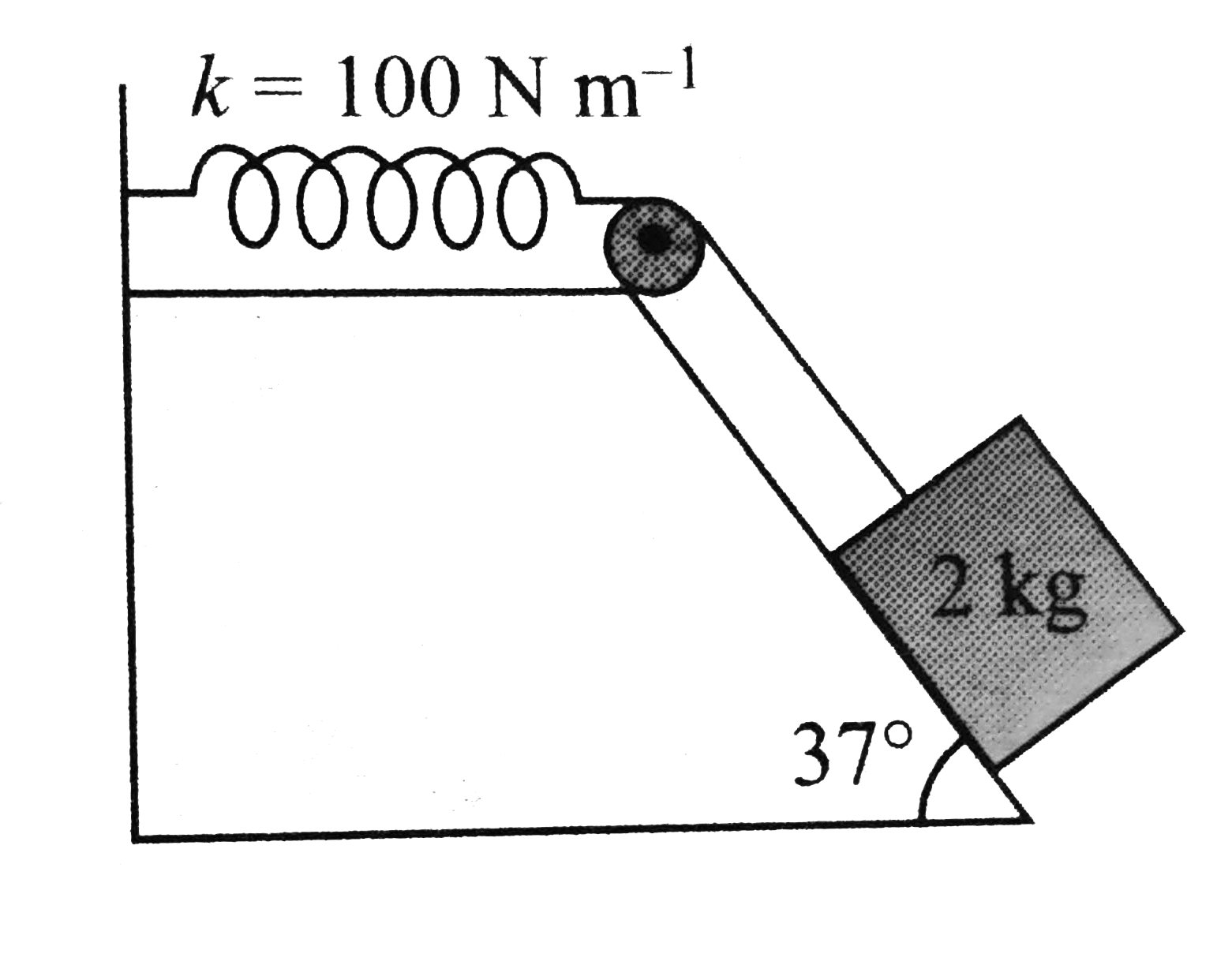
b. The experiment is repeated on a rough incline. If the block is observed to move 0.20m down along the incline before it comes to instantaneous rest, calculate the coefficient of kinetic friction.View SolutionQuestion 120
A ring of mass m=1kg can slide over a smooth vertical rod. A light string attached to the ring passing over a smooth fixed pulley at a distance of L=0.7m from the rod as shown in figure.
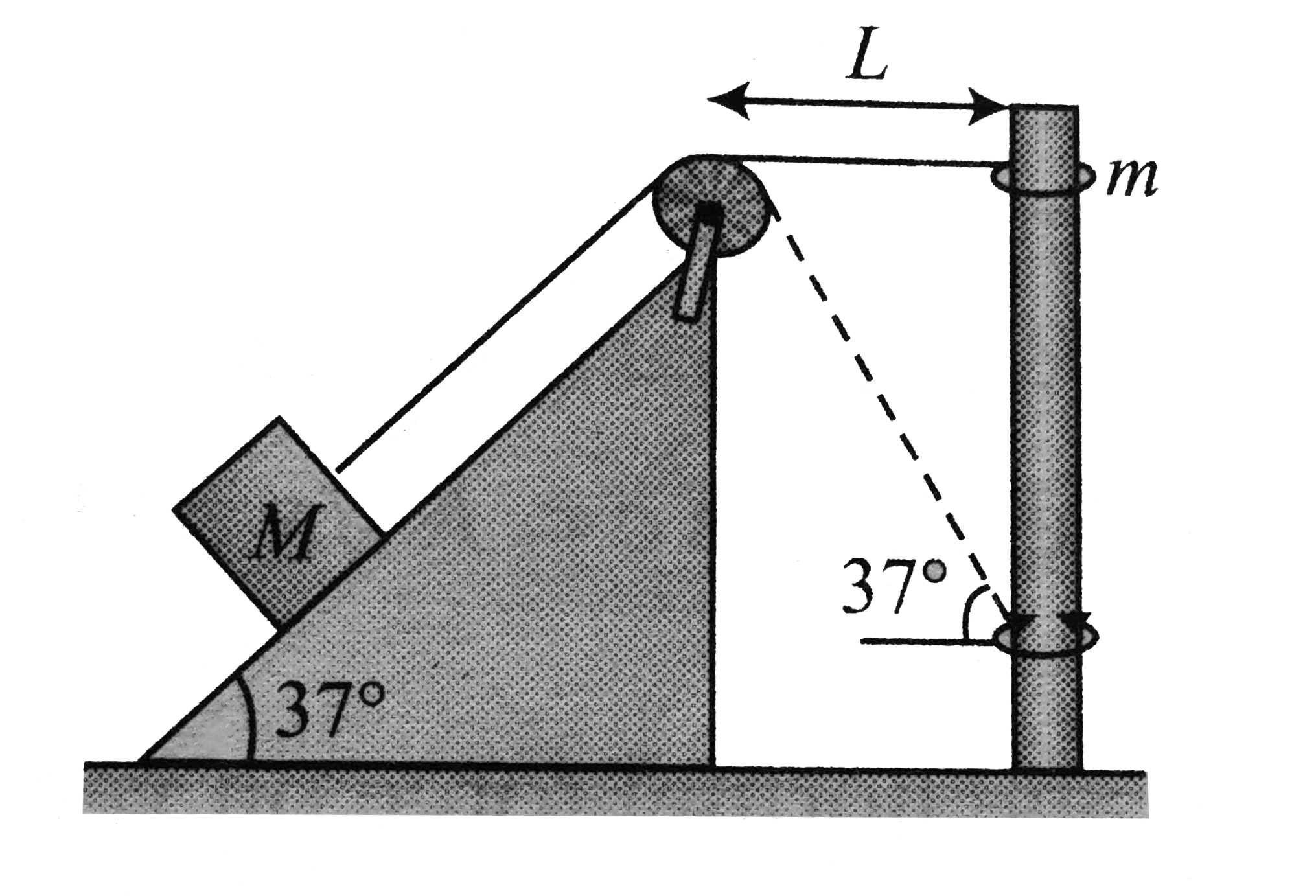
At the other end of the string mass M=5kg is attached, lying over a smooth fixed inclined plane of inclination angle 37∘. The ring is held in level with the pulley and released. Determine the velocity of ring when the string makes an angle (α=37∘) with the horizontal. [sin37∘=0.6]View SolutionQuestion 122
A block of mass m is released from rest onto a spring. A having stiffness kA=mg/2h as shown in figure. If the block compresses spring B through a distance h, find the:
a. stiffness of the spring B
b. equilibrium position of the block
c. maximum velocity of the block
d. maximum acceleration of the blockView SolutionQuestion 124
A vehicle of mass m starts moving along a horizontal circle of radius R such that its speed varies with distance s covered by the vehicle as c=K√s, where K is a constant. Calculate:
a. Tangential and normal force on vehicle as fucntion of s.
b. Distance s in terms of time t.
c. Work done by the resultant force in first t seconds after the beginning of motion. View SolutionQuestion 125
A block A of mass m is held at rest on a smooth horizontal floor. A light frictionless, small pulley is fixed at a height of 6m from the floor. A light inextensible string of length 16m, connected with A passes over the pulley and another identical block B is hung from the string. Initial height of B is 5m from the floor as shown in figure
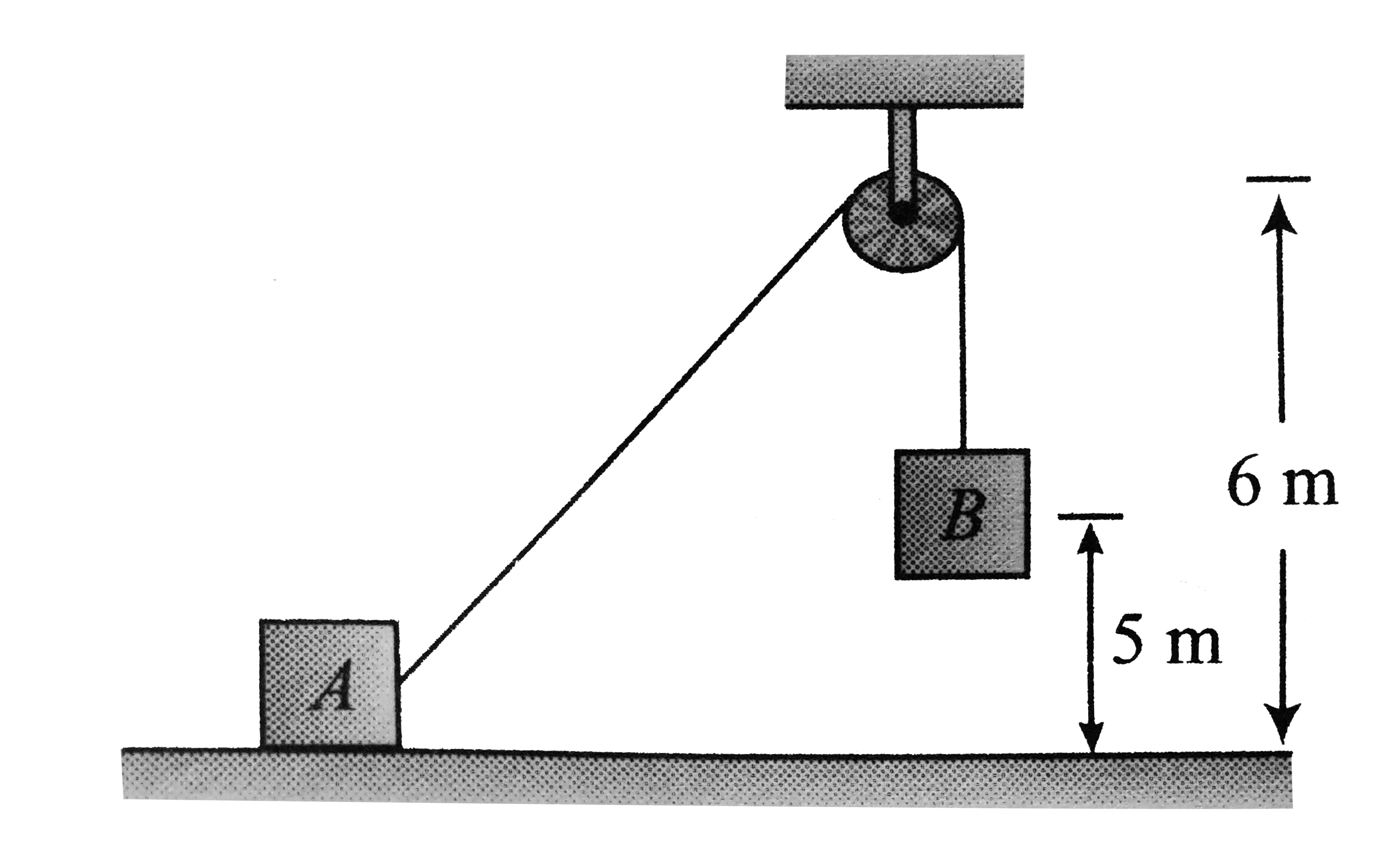
When the system is released from rest, B starts to move vertically downwards and A slides on the floor towards right.
a. If at an instant string makes an angle θ with horizontal, calculate relation between velocity u of A and v of B.
b. Calculate v when B strikes the floor. (g=10ms−2).View SolutionQuestion 127
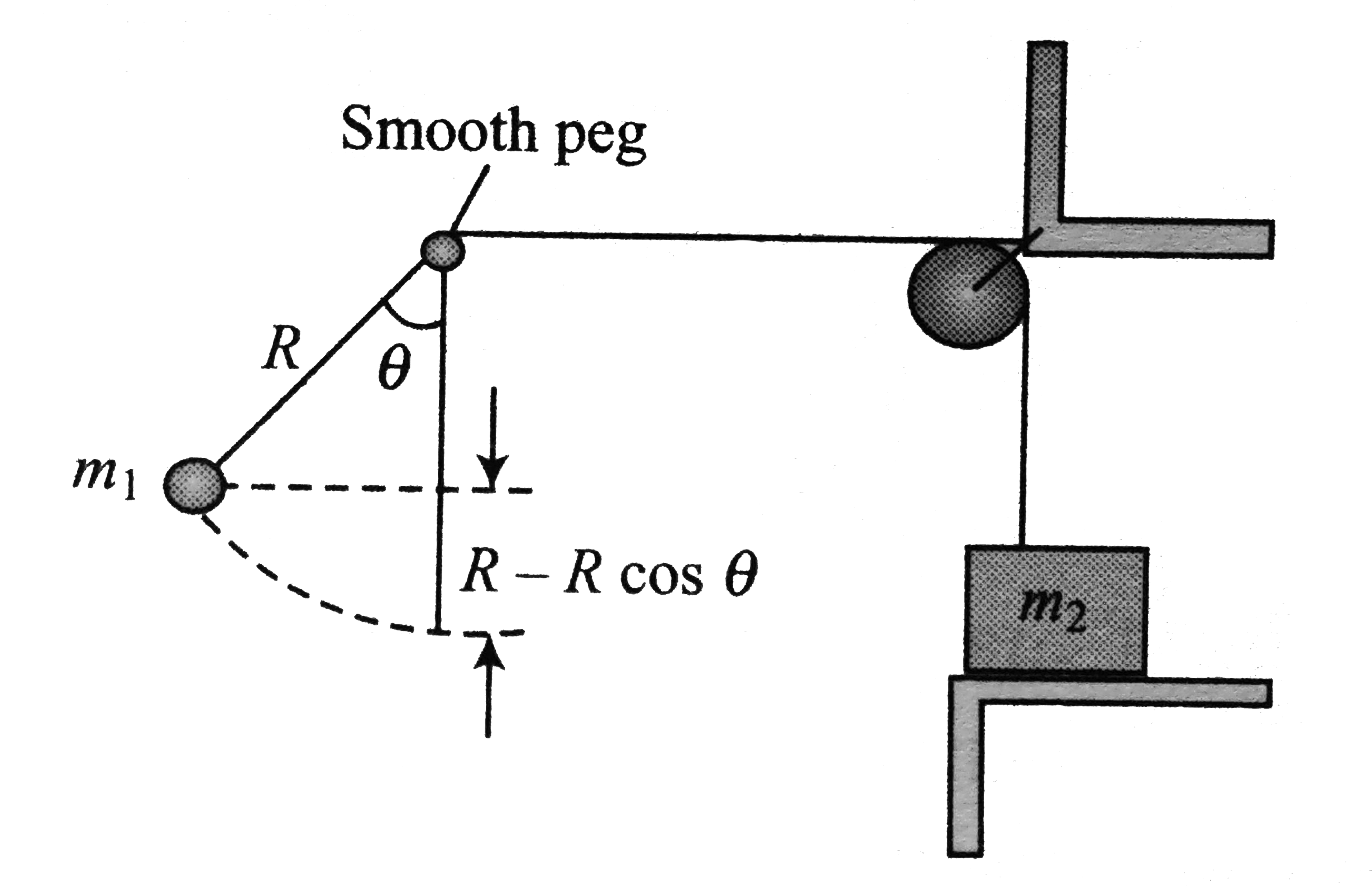
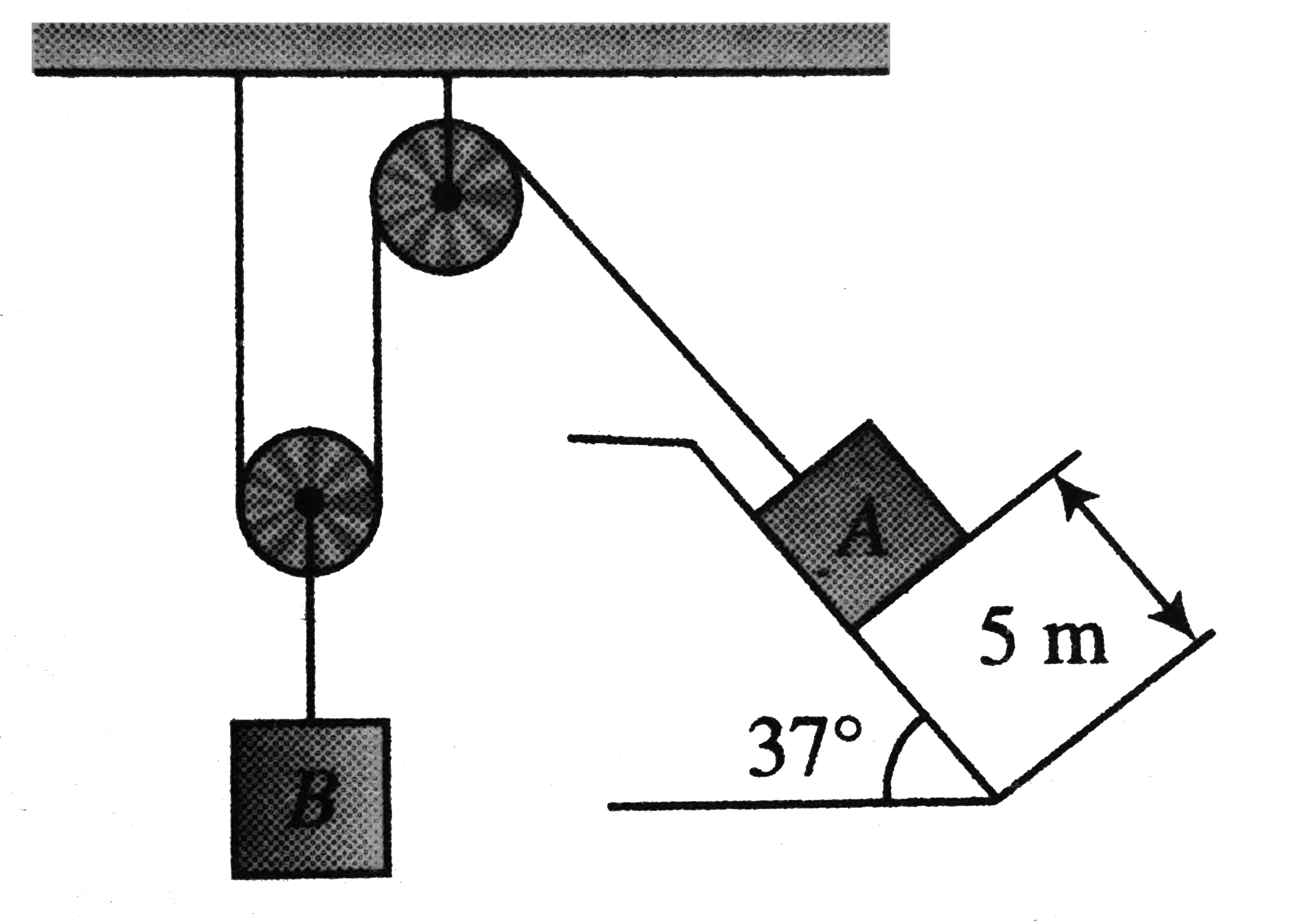
Two blocks are connected by a massless string that passes over a frictionless peg as shown in figure. One end of the string is attached to a mass m1=3kg, i.e., a distance R=1.20m from the peg. The other end of the string is connected to a block of mass m2=6kg resting on a table. From what angle θ, measured from the vertical, must the 3−kg block be released in order to just lift the 6kg block off the table?
 View Solution
View SolutionQuestion 128
A bob of mass m is projected with a horizontal velocity v=√gl2 as shown in figure. In consequence, it moves in a circular path in a vertical plane by the inextensible string which passes over the smooth fixed peg. Find the maximum angle that the bob swings in the left hand side.
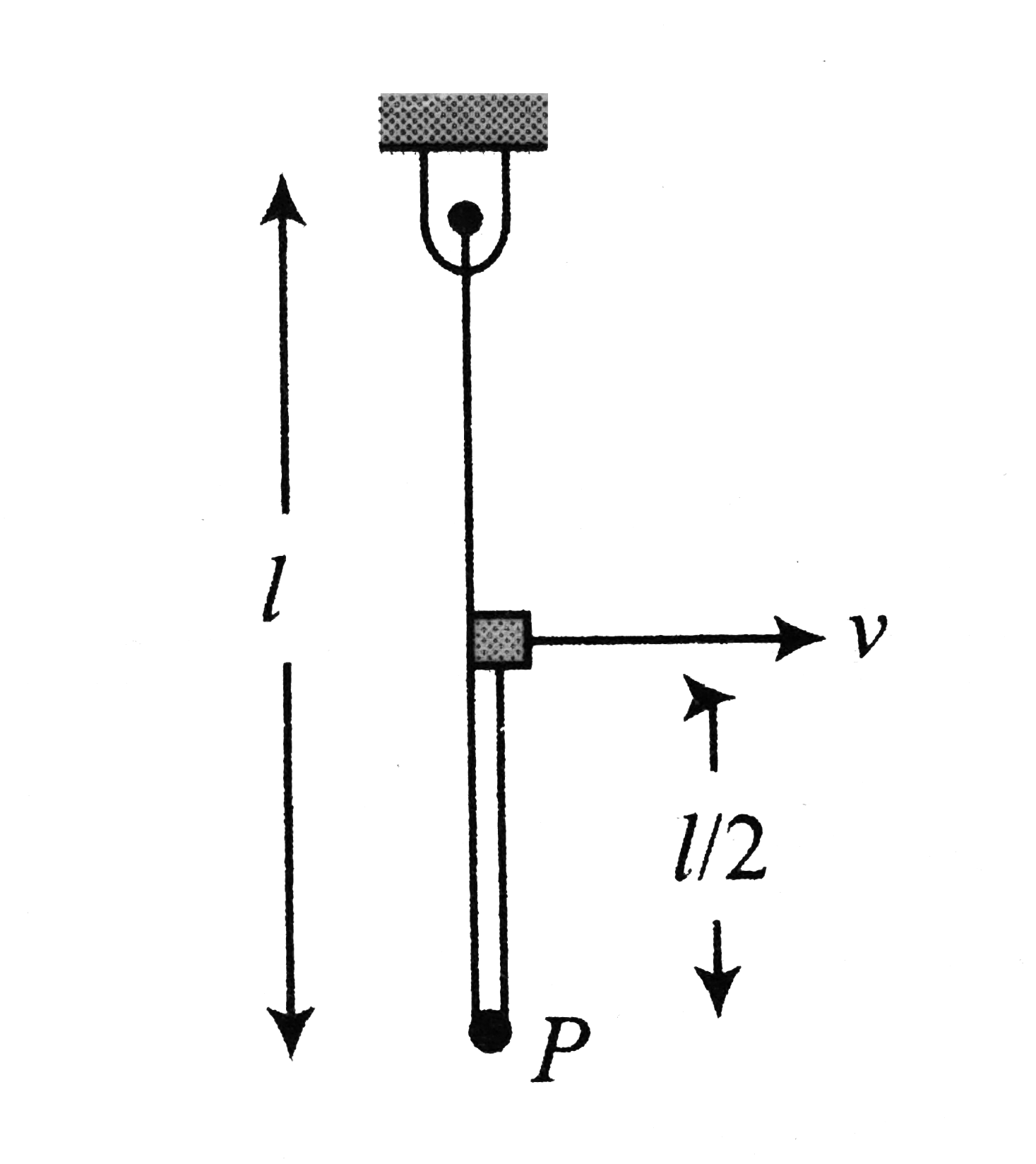 View Solution
View SolutionQuestion 129
A block is projected with a speed v0 such that it strikes the point of projection after describing the path as shown by the dotted line. If friction exists for the parth of length d and the vertical circular path is smooth, assuming μ=coefficient of friction,
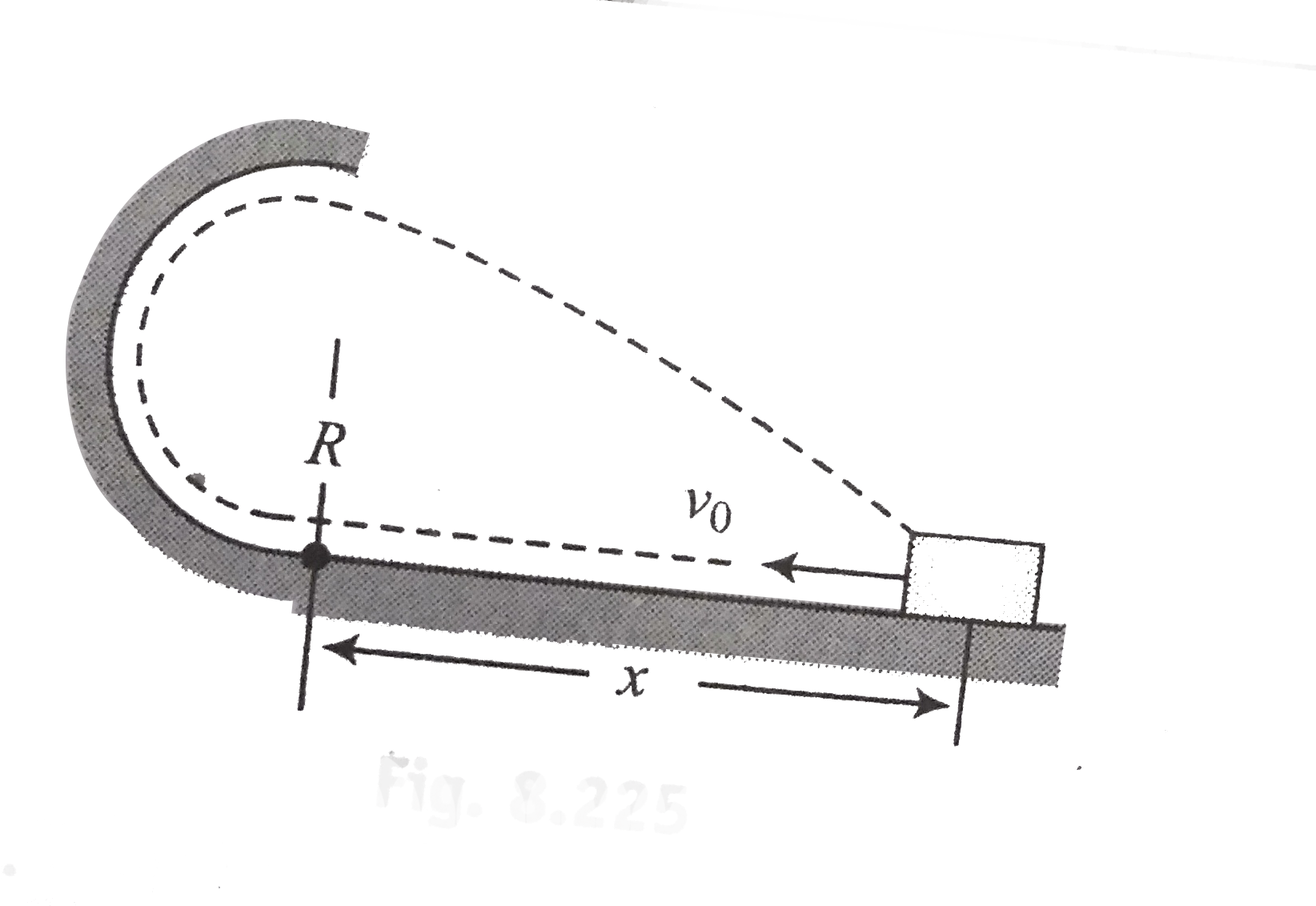
a. Find v0.
b. What is the minimum value of v0?View SolutionQuestion 130
A small ball is suspended from point O by a thread of length l. A nail is driven into the wall at a distance of l/2 below O, at A. The ball is drawn aside so that the thread takes up a horizontal position at the level of point O and then released. Find
a. At what angle from the vertical of the ball's trajectory, will the tension in the thread disappear?
b. What will be the highest point from the lowermost point of circular track, to which it will rise?View SolutionQuestion 131
The displacement x of particle moving in one dimension, under the action of a constant force is related to the time t by the equation t=√x+3
where xis∈metersandt∈seconds . Find
(i) The displacement of the particle when its velocity is zero , and
(ii) The work done by the force in the first 6seconds. View SolutionQuestion 134
Two identical 5kg blocks are moving with same speed of 2ms−1 towards each other along a frictionless horizontal surface. The two blocks collide, stick together, and come to rest. Consider the two blocks as a system. The works done by external and internal forces are, respectively,View SolutionQuestion 143
A bus can be stopped by applying a retarding force F when it is moving with speed v on a level road. The distance covered by it before coming to rest is s. If the load of the bus increase by 50% because of passengers, for the same speed and same retarding force, the distance covered by the bus to come to rest shall be View SolutionQuestion 153
An object of mass m slides down a hill of height h of arbitrary shape and after travelling a certain horizontal path stops because of friction. The friction coefficient is different for different segments for the entire path but is independent of the velocity and direction of motion. The work that a force must perform to return the object to its initial position along the same path is View SolutionQuestion 155
A block of 4kg mass starts at rest and slides a distance d down a friction less incline ( angle 30∘) where it runs into a spring of negligible mass. The block slides an additional 25cm before it is brought to rest momentarily by compressing the spring. The force constant of the spring is 400Nm−1. The value of d is (take g=10ms−2)
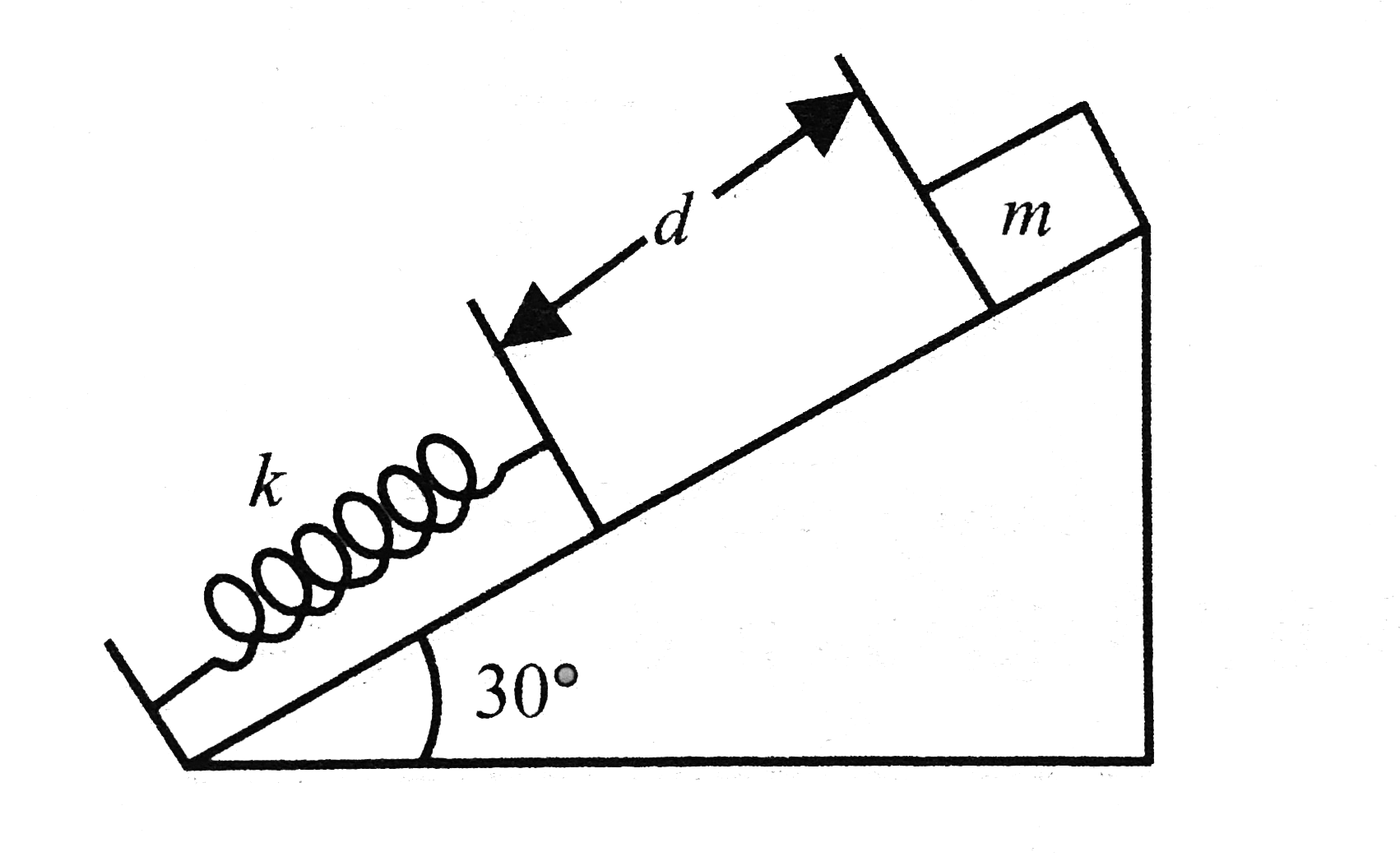 View Solution
View SolutionQuestion 157
A spring is compressed between two toy carts to masses m1 and m2. When the toy carts are released, the spring exerts on each toy cart equal and opposite forces for the same small time t. If the coefficients of friction μ between the ground and the toy carts are equal, then the magnitude of displacements of the toy carts are in the ratioView SolutionQuestion 158
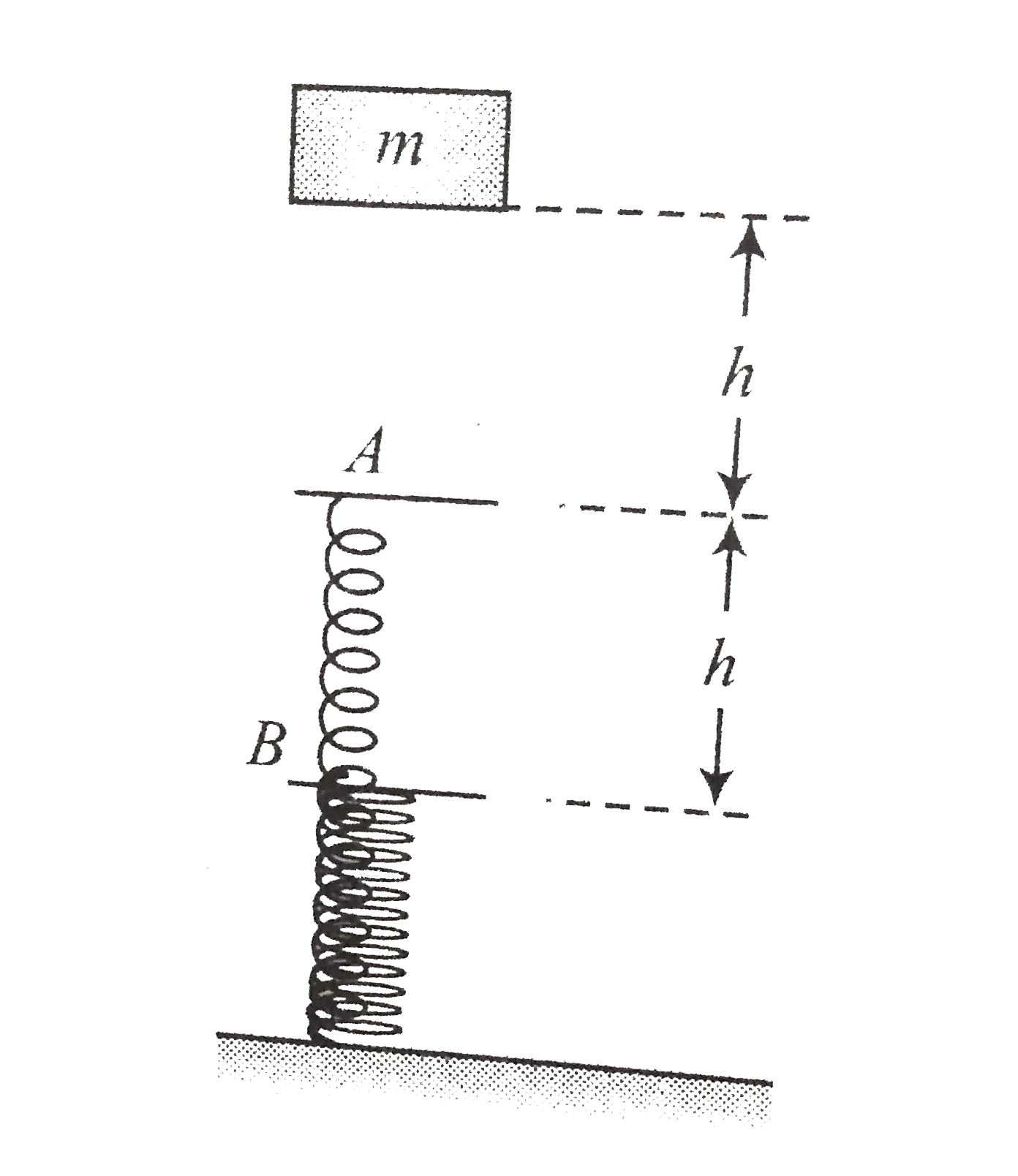
A massless platform is kept on a light 0.1 kg elastic spring, as shown in the figure When particle of mass 0.1 kg is dropped on the pan from a height of 0.24 m, the particle strikes the pan, and the spring is compressed by 0.01 m. From what height should the particle be dropped to cause a compression of 0.04 m ?
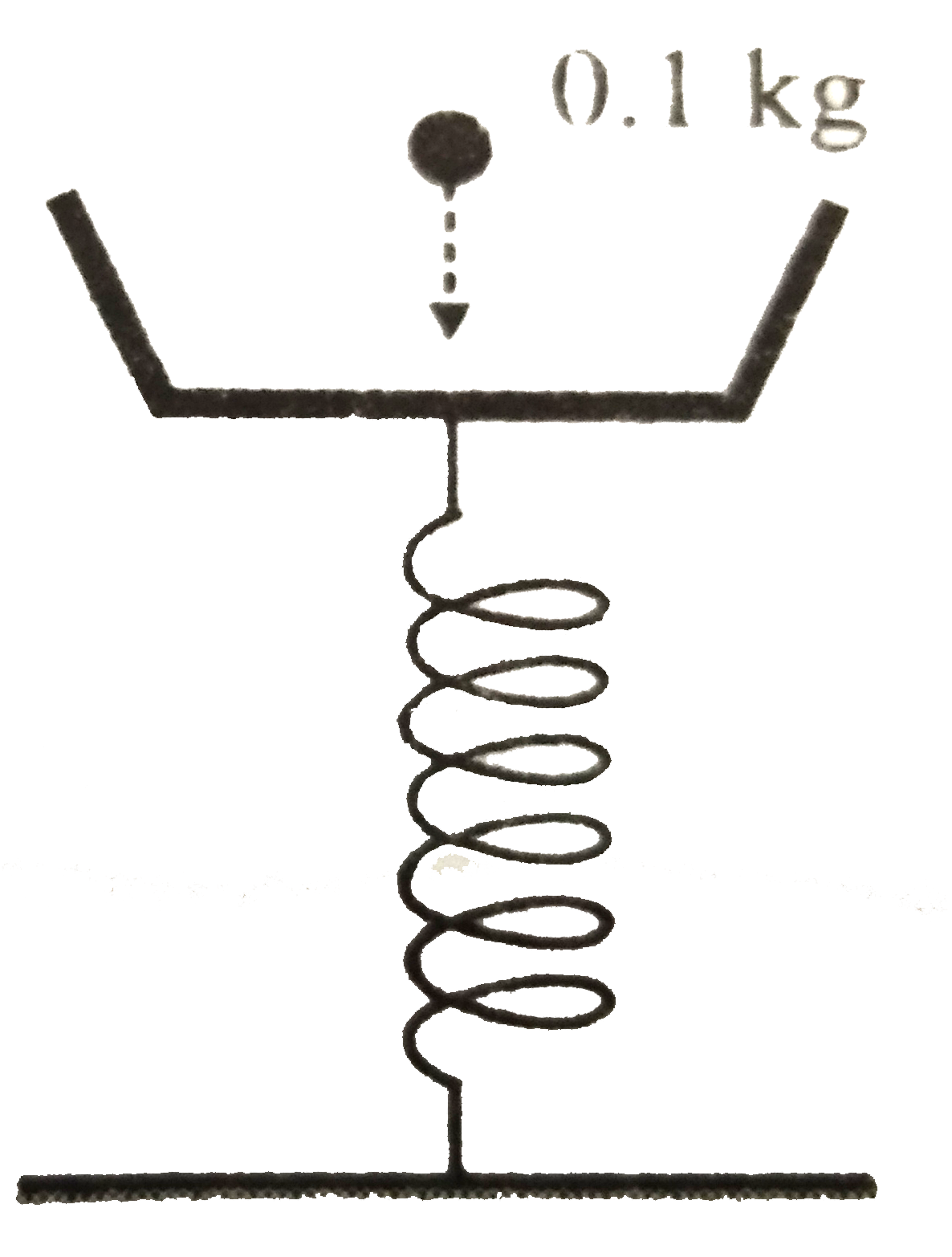 View Solution
View SolutionQuestion 159
A partical is realeased from the top of two inclined rought surface of height h each. The angle of inclination of the two planes are 30∘ and 60∘ respectively. All other factors (e.g. coefficient of friction , mass of the block etc) are same in both the cases. Let K1andK2 be the kinetic energy of the partical at the bottom of the plane in two cases. Then View SolutionQuestion 166
A large slab of mass 5kg lies on a smooth horizontal surface, with a block of mass 4kg lying on the top of it. The coefficient of friction between the block and the slab is 0.25. If the block is pulled horizontally by a force of F =6N, the work done by the force of friction on the slab, between the instants t=2s and t=3s, is (g=10ms−2)
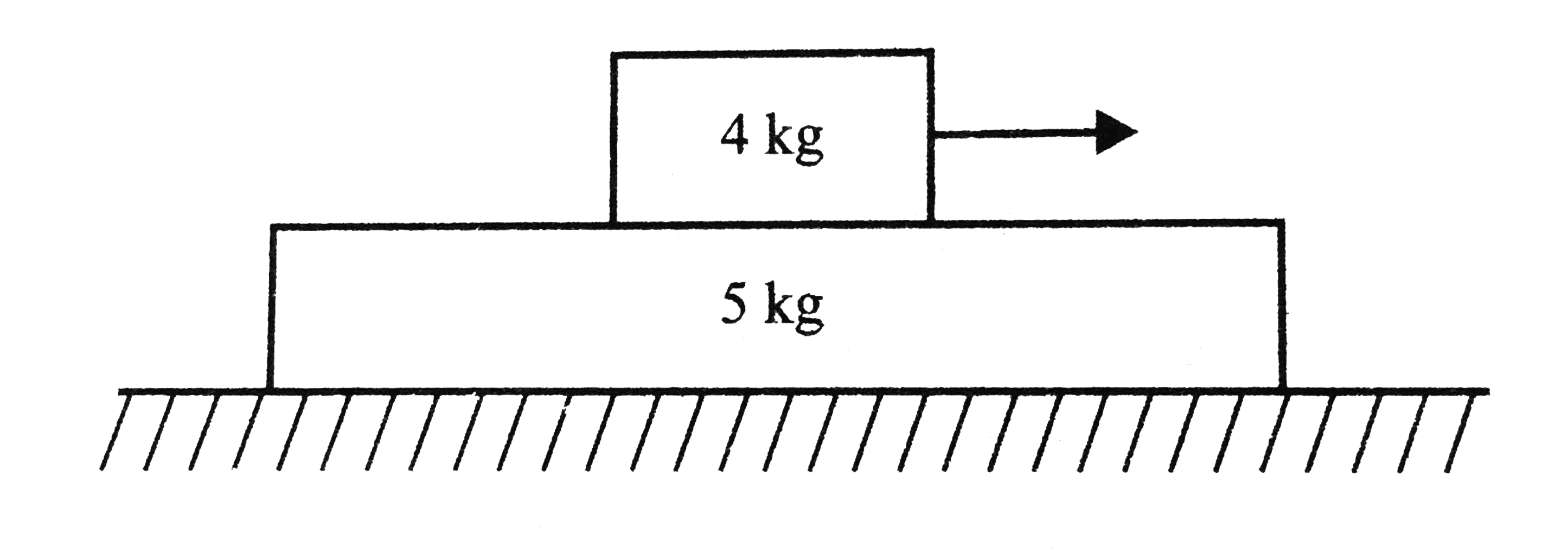 View Solution
View SolutionQuestion 167
A small block of mass 2kg is kept on a rough inclined surface of inclination θ=30∘ fixed in a lift. The lift goes up with a uniform speed of 1ms−1 and the block does not slide relative to the inclined surface. The work done by the force of friction on the block in a time interval of 2s isView SolutionQuestion 171
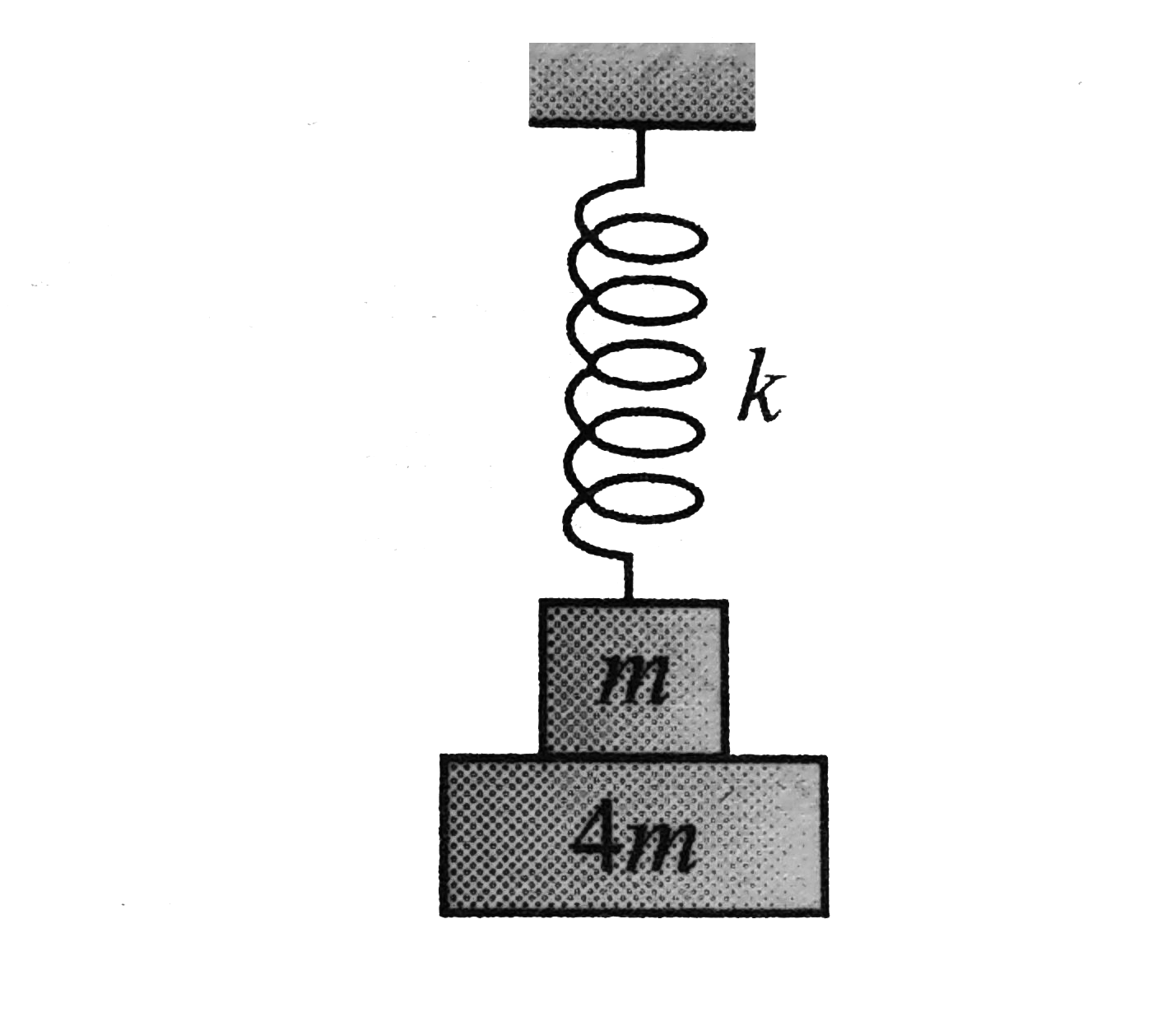
Two discs, each having mass m, are attached rigidly to the ends of a vertical spring. One of the discs rests on a horizontal surface and the other produces a compression x0 on the spring when it is in equilibrium. How much further must the spring be compressed so that when the force causing compression is removed, the extension of the spring will be able to lift the lower disc off the table?
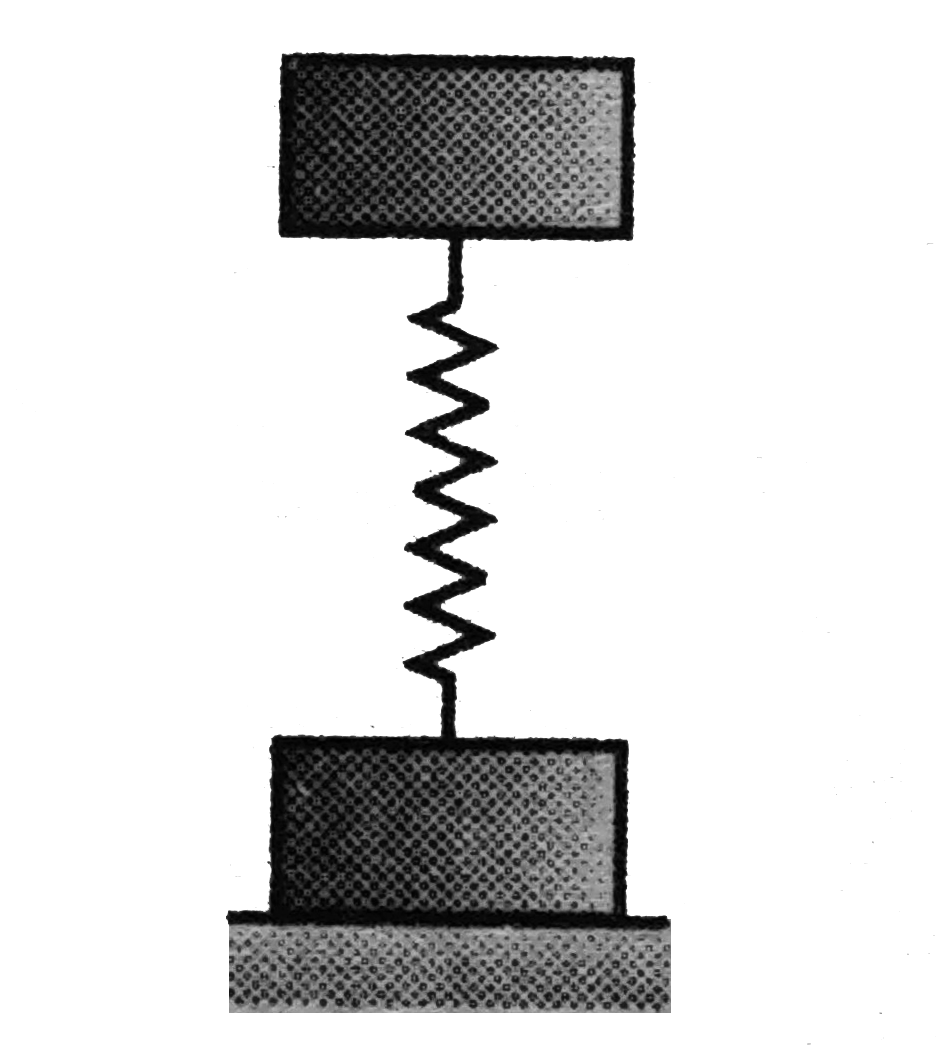 View Solution
View SolutionQuestion 173
A block m is kept stationary on the surface of an accelerating cage as shown in figure. At the given instant, study the following statetments regarding the block.
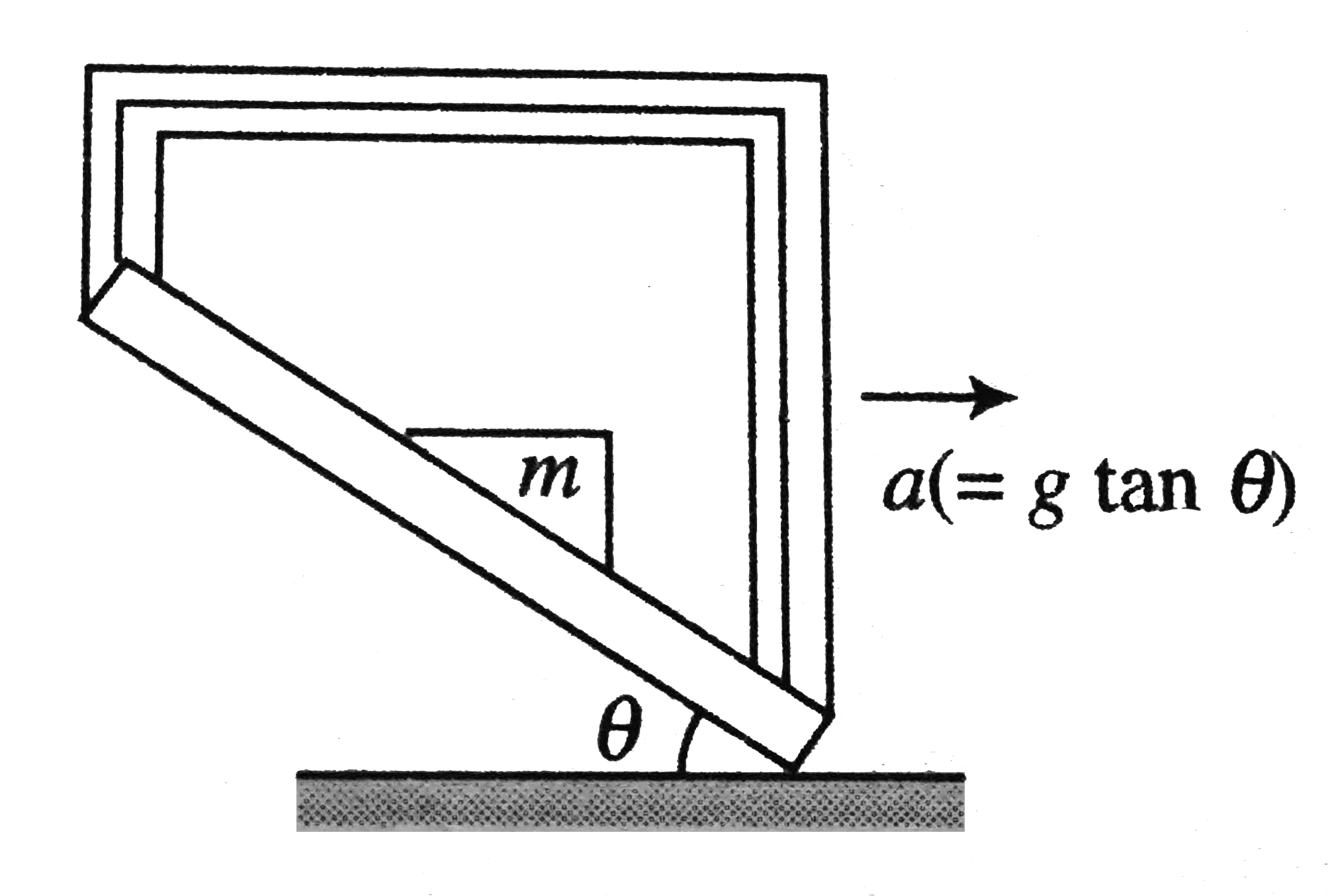
i. Normal reaction performs positive work on the block.
ii. Frictional work done on the block is negative.
iii. No net work is done by normal reaction and friction on the block.
Now mark the correct answer.View SolutionQuestion 177
A collar B of mass 2kg is constrained to move along horizontal smooth and fixed circular track of radius 5 m and having spring constant 200Nm−1 is underformed when the collar is at A. If the collar starts from rest at B the normal reaction exerted by the track on the collar when it passes through A is
 View Solution
View SolutionQuestion 179
A particle is projected along a horizontal field whose coefficient of friction varies as μ=A/r2, where r is the distance from the origin in meters and A is a positive constant. The initial distance of the particle is 1m from the origin and its velocity is radially outwards. The minimum initial velocity at this point so the particle never stops is View SolutionQuestion 180
Two identical blocks A and B are placed on two inclined planes as shown in figure. Neglect resistance and other friction.
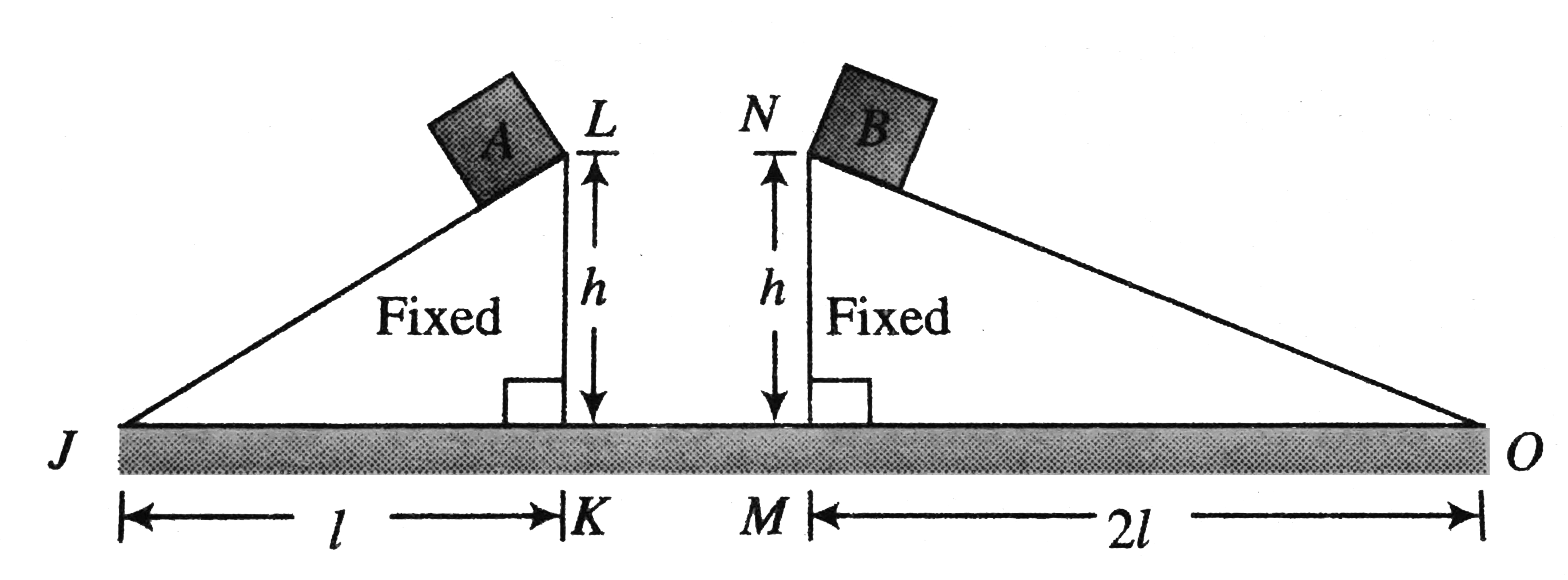
Read the following statements and choose options.
Statement I: The kinetic energy of A on sliding to J will be greater than the kinetic of B on sliding to O.
Statement II: The acceleration of A will be greater than acceleration of B when both are released on the inclined plane.
Statement III: The work done by external agent to move the block slowly from position B to O is negative.View SolutionQuestion 187
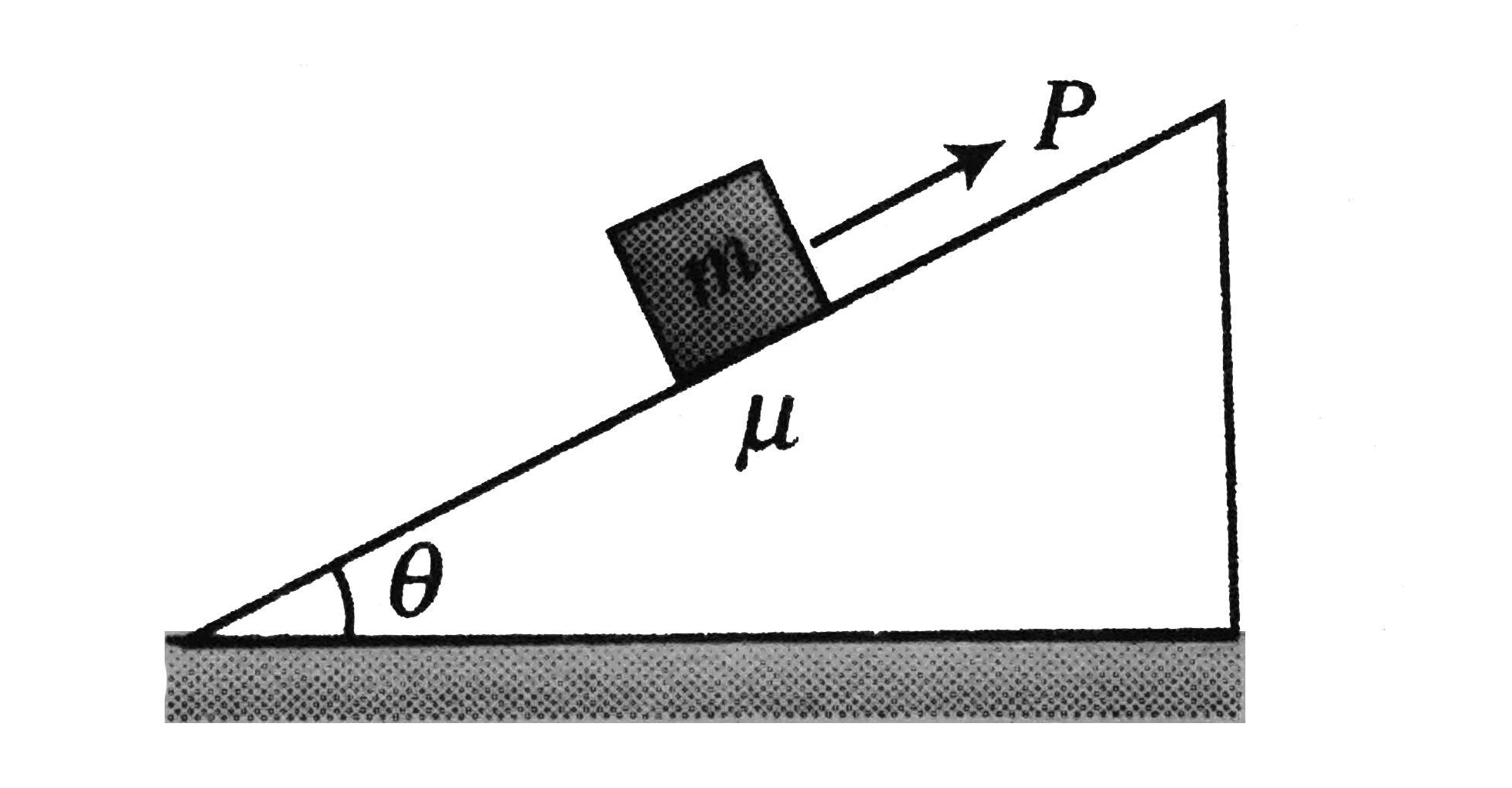
A block of mass m is attached with a massless spring of force constant k. The block is placed over a rough inclined surface for which the coefficient of friction is μ=34. The minimum value of M required to move the block up the plane is (Neglect mass of string, mass of pulley and friction in pulley)
 View Solution
View SolutionQuestion 190
A particle is projected vertically upwards with a speed of 16ms−1. After some time, when it again passes through the point of projection, its speed is found to be 8ms−1. It is known that the work done by air resistance is same during upward and downward motion. Then the maximum height attained by the particle is (take g=10ms−2)View SolutionQuestion 201
The potential energy of a particle is determined by the expression U=α(x2+y2), where α is a positive constant. The particle begins to move from a point with the co-ordinates (3, 3) only under the action of potential fields force. When it reaches the point
(1, 1) its kinetic energy is 4Kα. Find the value of K.View SolutionQuestion 202
In the position shown in figure, the spring is at its natural length. The block of mass m is given a velocity v0 towards the vertical support at t=0. The coefficient of friction between the block and the surface is given by μ=αx, where α is a positive constant and x is the position of the block from its starting position. The block comes to rest for the first time at x, which is
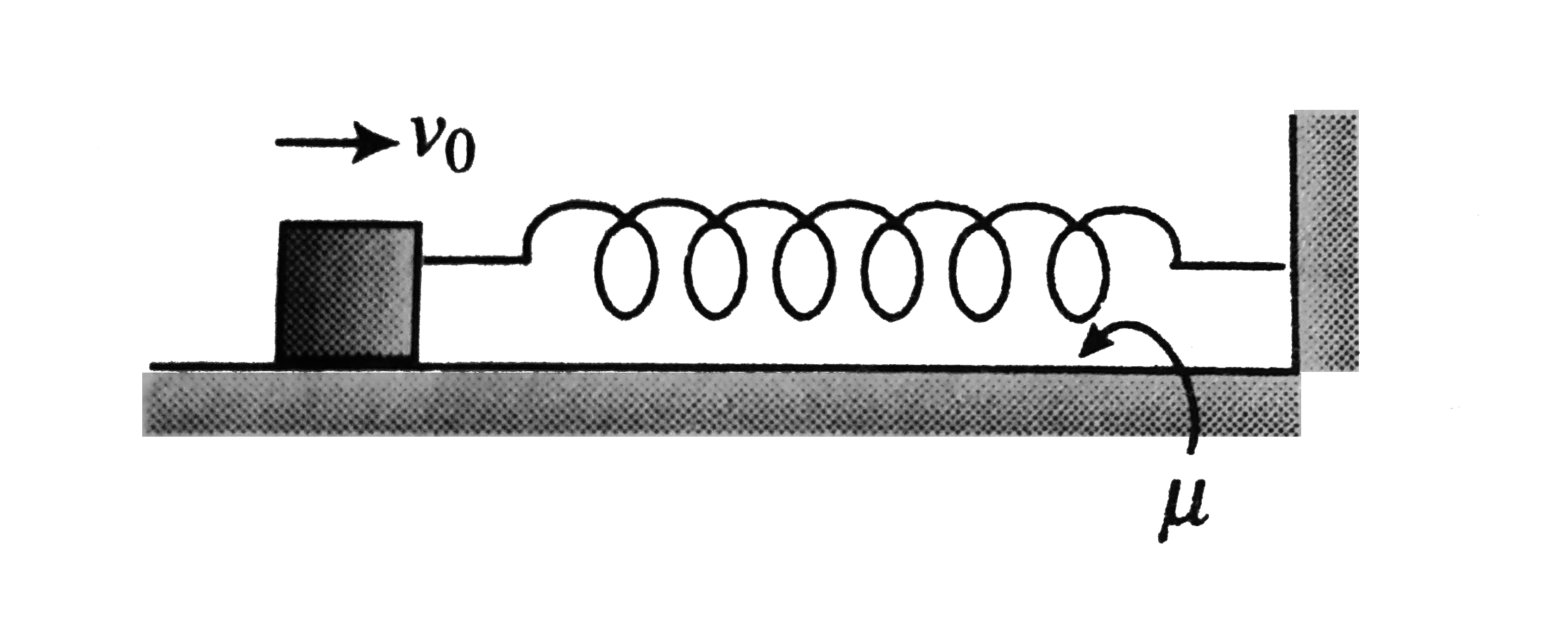 View Solution
View SolutionQuestion 203
In the figure shown, a spring of spring constant K is fixed at on end and the other end is attached to the mass 'm' . The coefficient of friction between block and the inclined plane is μ. The block is released when the spring is in tis natural length. Assuming that the θ>μ, the maximum speed of the block during the motion is.
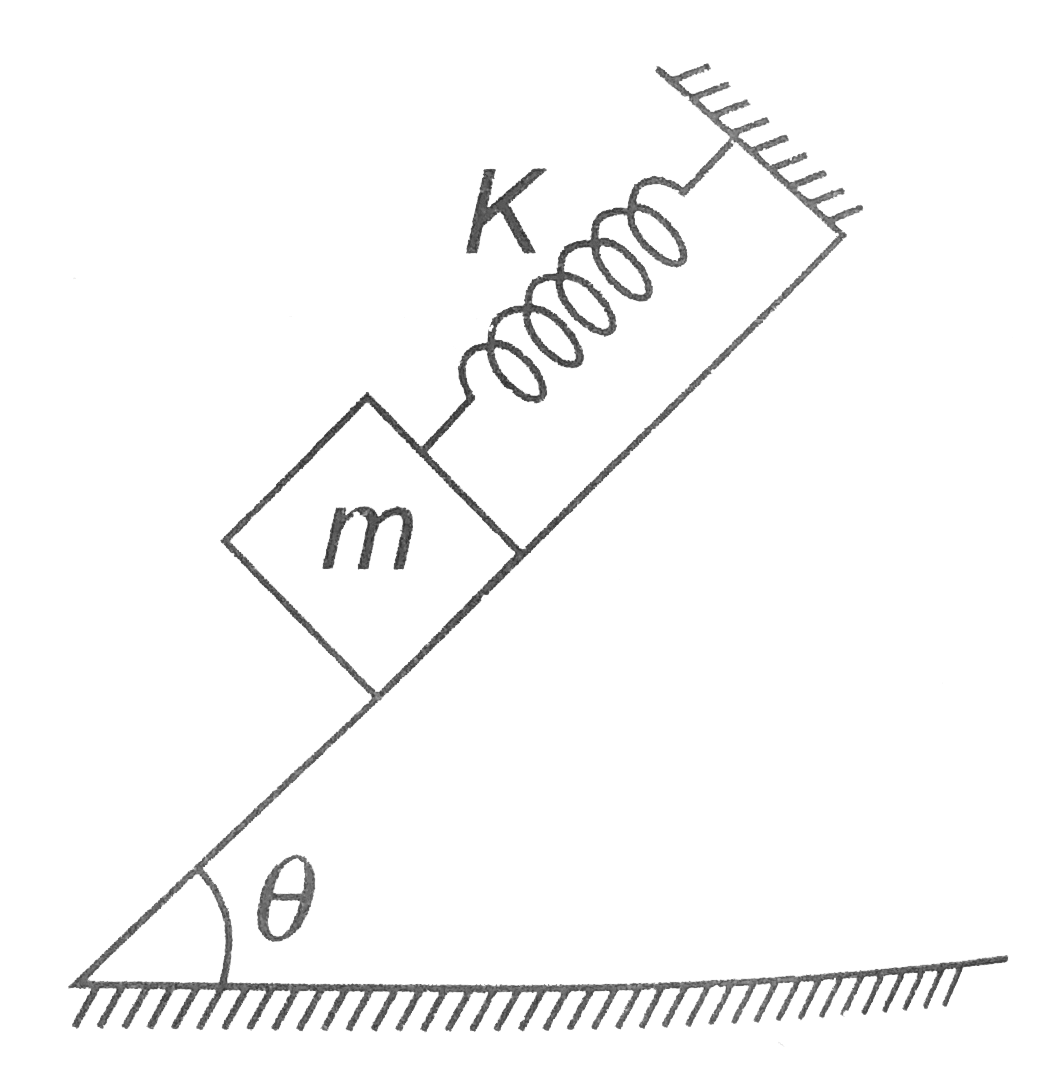 View Solution
View SolutionQuestion 204
Let r be the distance of a particle from a fixed point to which it is attracted by an inverse square law force given by F=k/r2 (k=constant). Let m be the mass of the particle and L be its angular momentum with respect to the fixed point. Which of the following formulae is correct about the total energy of the system?View SolutionQuestion 206
A particle of mass m slides along a curved-flat-curved track. The curved portions of the track are smooth. If the particle is released at the top of one of the curved portions, the particle comes to rest at flat portion of length l and of μ=μkinetic after covering a distance of
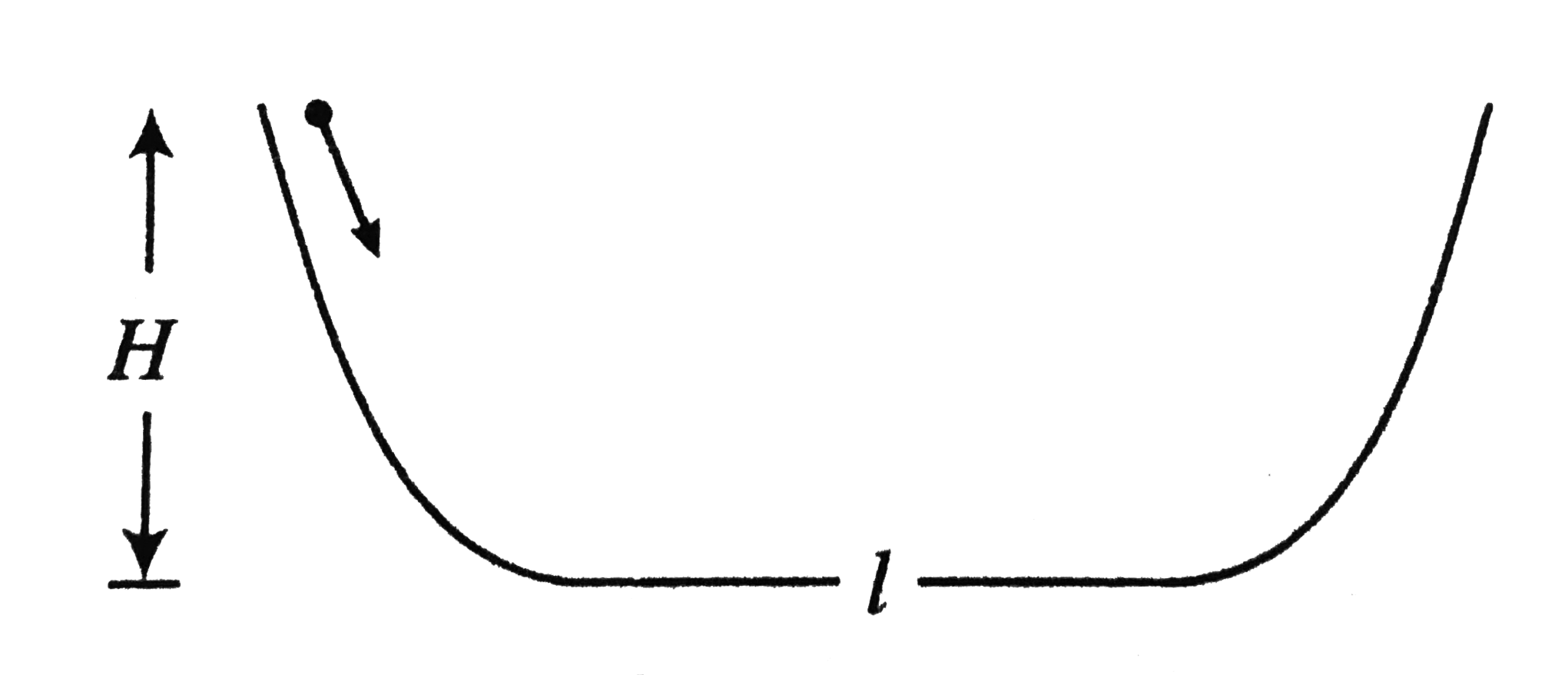 View Solution
View SolutionQuestion 207
A block of mass m has initial velocity u having direction towards +x axis. The block stops after covering a distnce S causing similar extension in the spring of constant K holding it. If μ is the kinetic friction between the block and the surface on which it was moving, the distance S is given
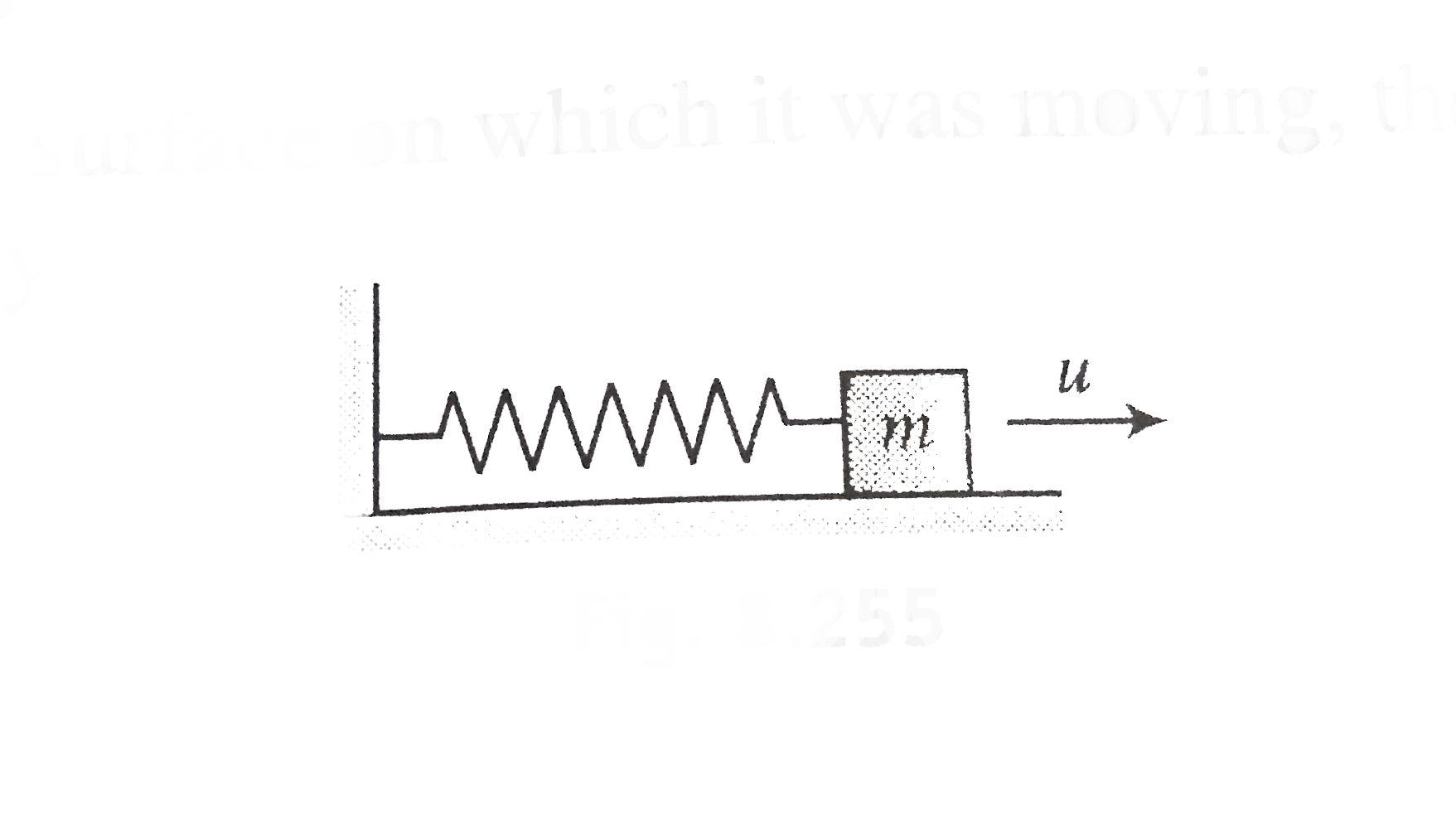 View Solution
View SolutionQuestion 209
A rope ladder of length L is attached to a balloon of mass M. As the man of mass m climbs the ladder into the balloon basket, the balloon comes down by a vertical distance s. Then the increase in potential energy of man divided by the increase in potential energy of balloon is
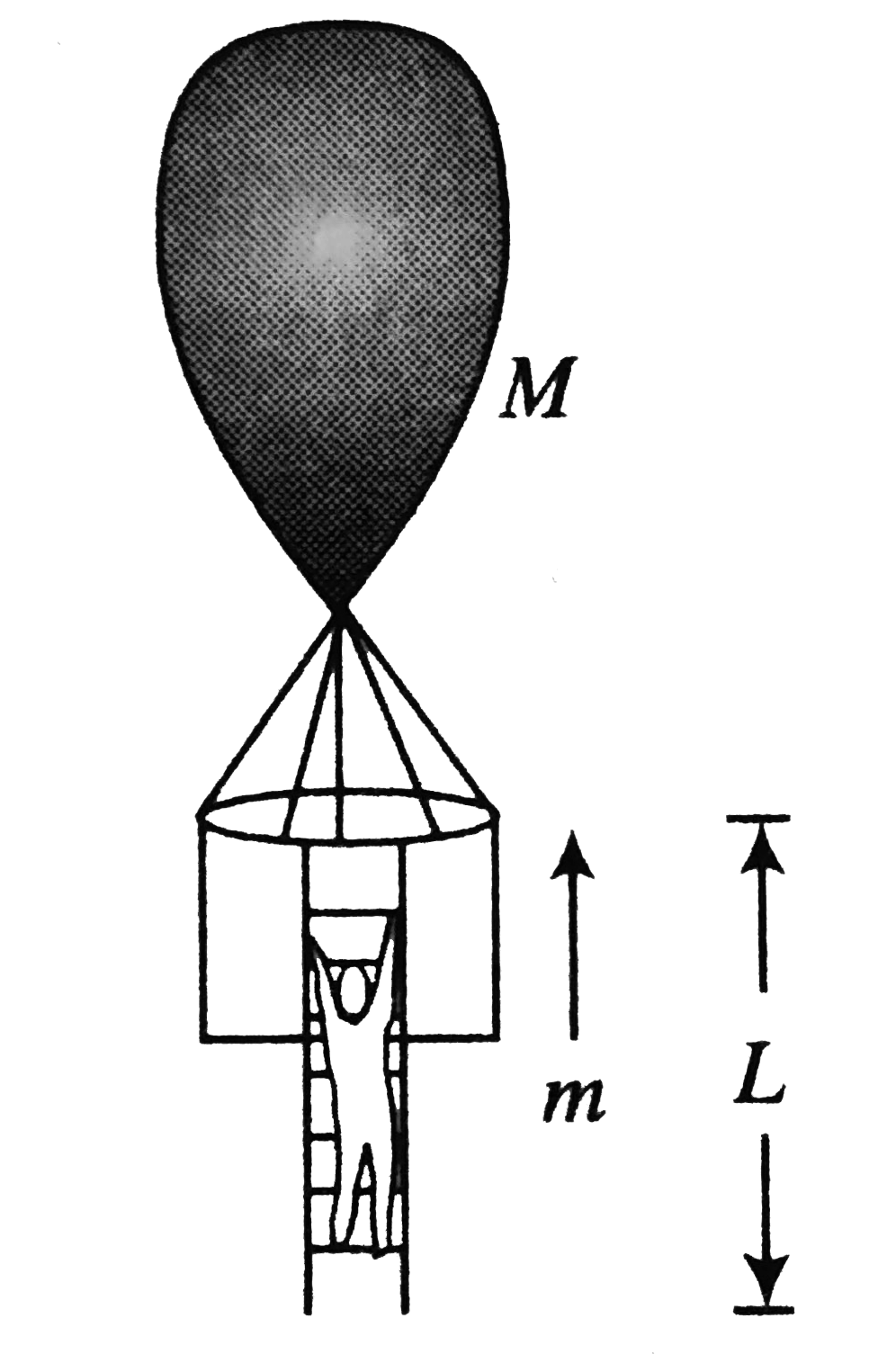 View Solution
View SolutionQuestion 213
A simple pendulum consisting of a mass M attached to a string of length L is released from rest at an angle α. A pin is located at a distance l below the pivot point. When the pendulum swings down, the string hits the pin as shown in figure. The maximum angle θ which the string makes with the vertical after hitting the pin is
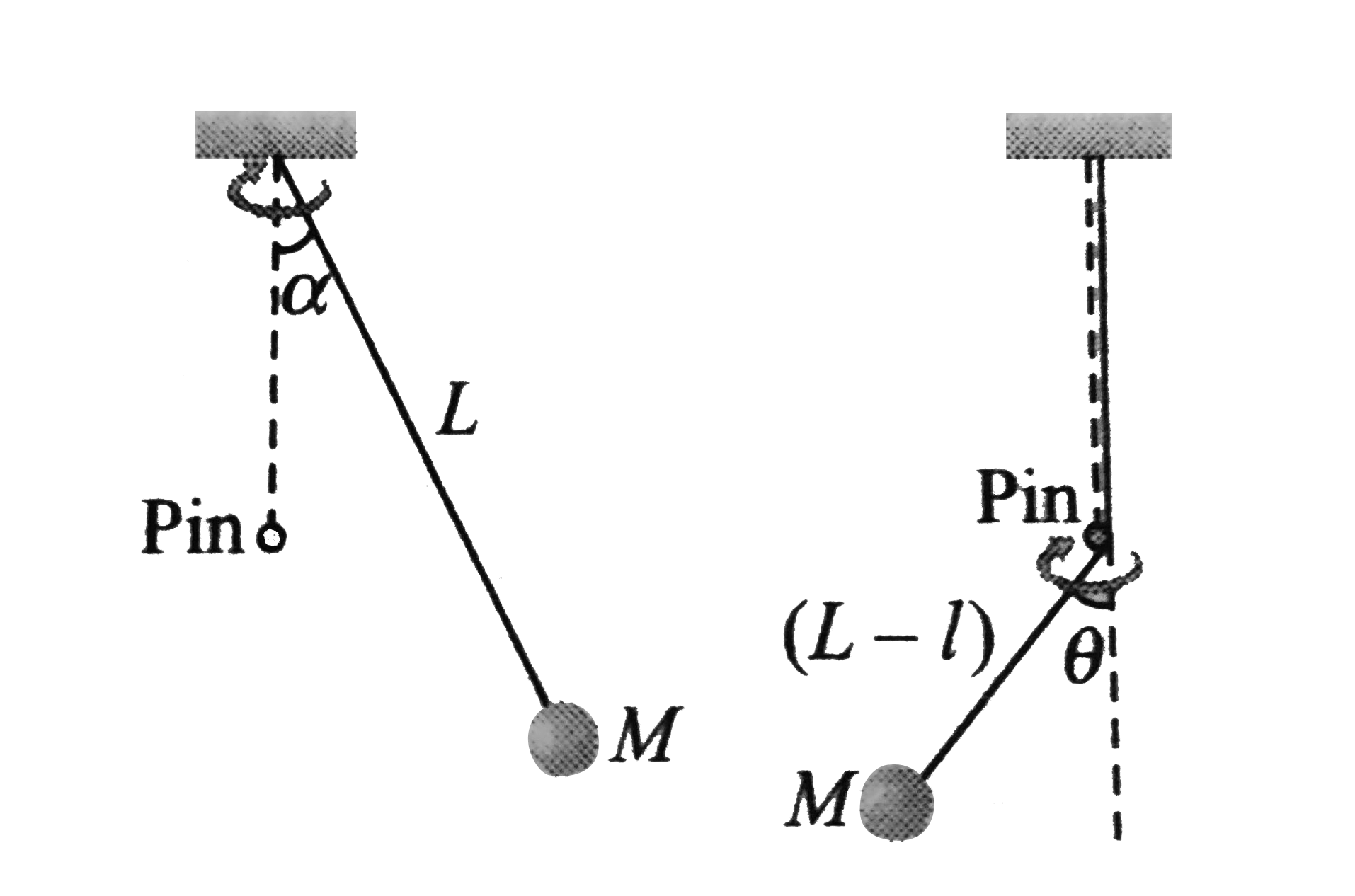 View Solution
View SolutionQuestion 214
Two bodies of masses m and 4m are attached to a light string as shown in figure. A body of mass m hanging from string is executing oscillations with angular amplitude 60∘, while other body is at rest on a horizontal surface. The minimum coefficient of friction between mass 4m and the horizontal surface is (here pulley is light and smooth)
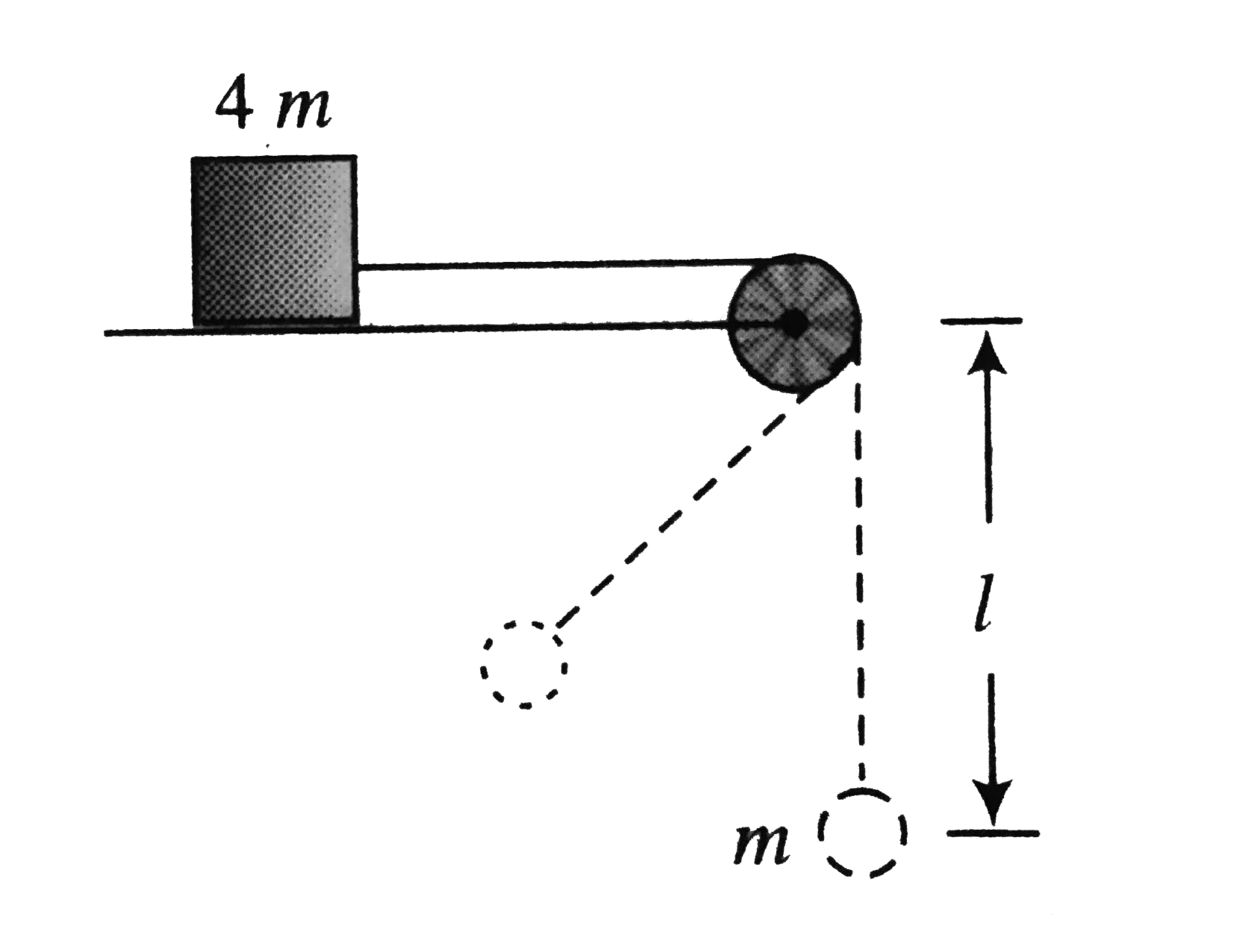 View Solution
View SolutionQuestion 220
A block of mass m is connected to a spring of spring constant k as shown in figure. The frame in which the block is placed is given an acceleration a towards left. Neglect friction between the block and the frame walls. The maximum velocity of the block relative to the frame is
 View Solution
View SolutionQuestion 222
A 20−kg block attached to a spring of spring constant 5Nm−1 is released from rest at A. The spring at this instant is having an elongation of 1m. The block is allowed to move in smooth horizontal slot with the help of a constant force 50N in the rope as shown. The velocity of the block as it reaches B is (assume the rope to be light)
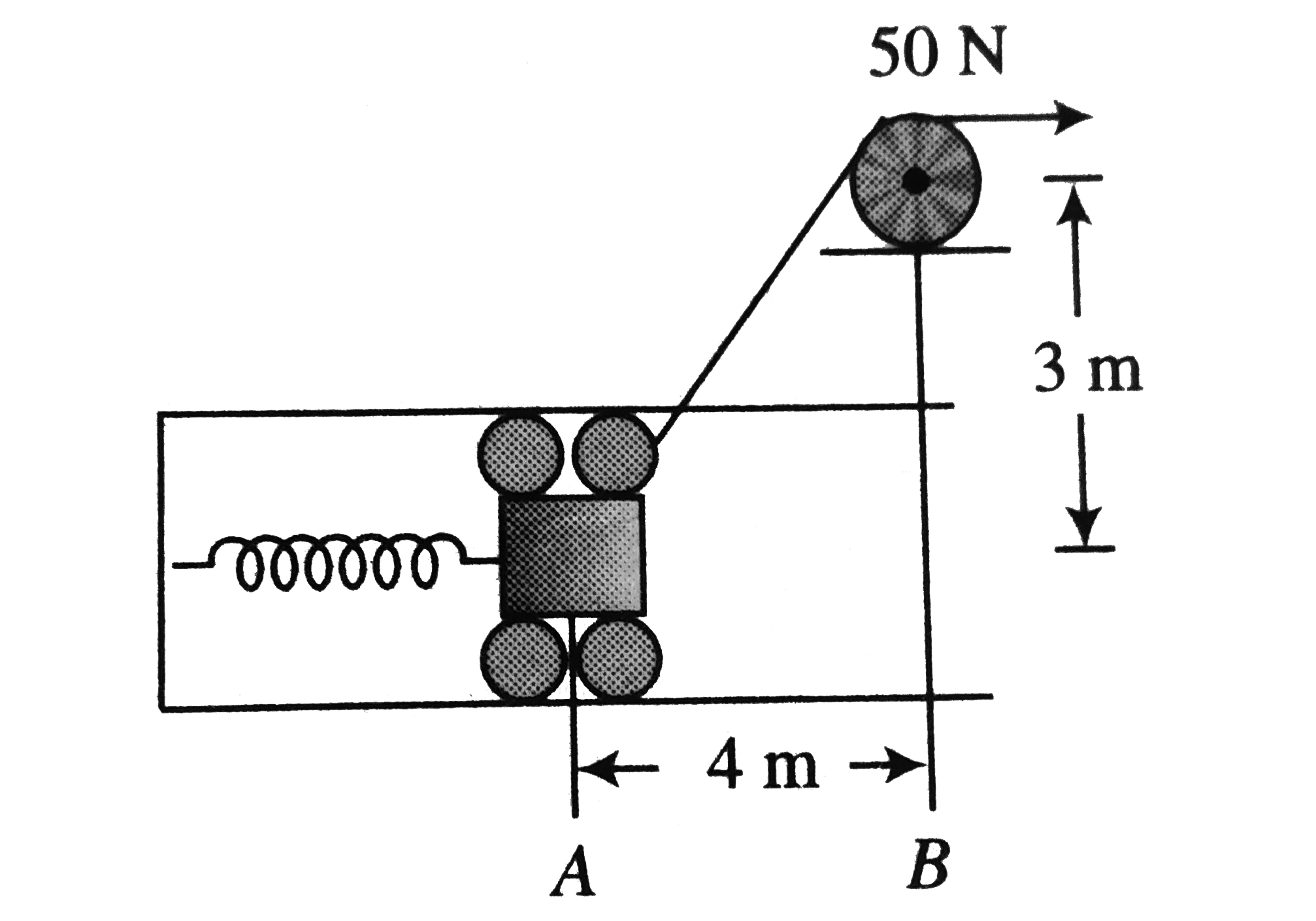 View Solution
View SolutionQuestion 223
Two identical blocks, each having mass M, are placed as shown in figure. These two blocks A and B are smoothly conjugated, so that when another block C of mass m passes from A to B there is no jerk. All the surfaces are frictionless, and all three blocks are free to move. Block C is released from rest, then
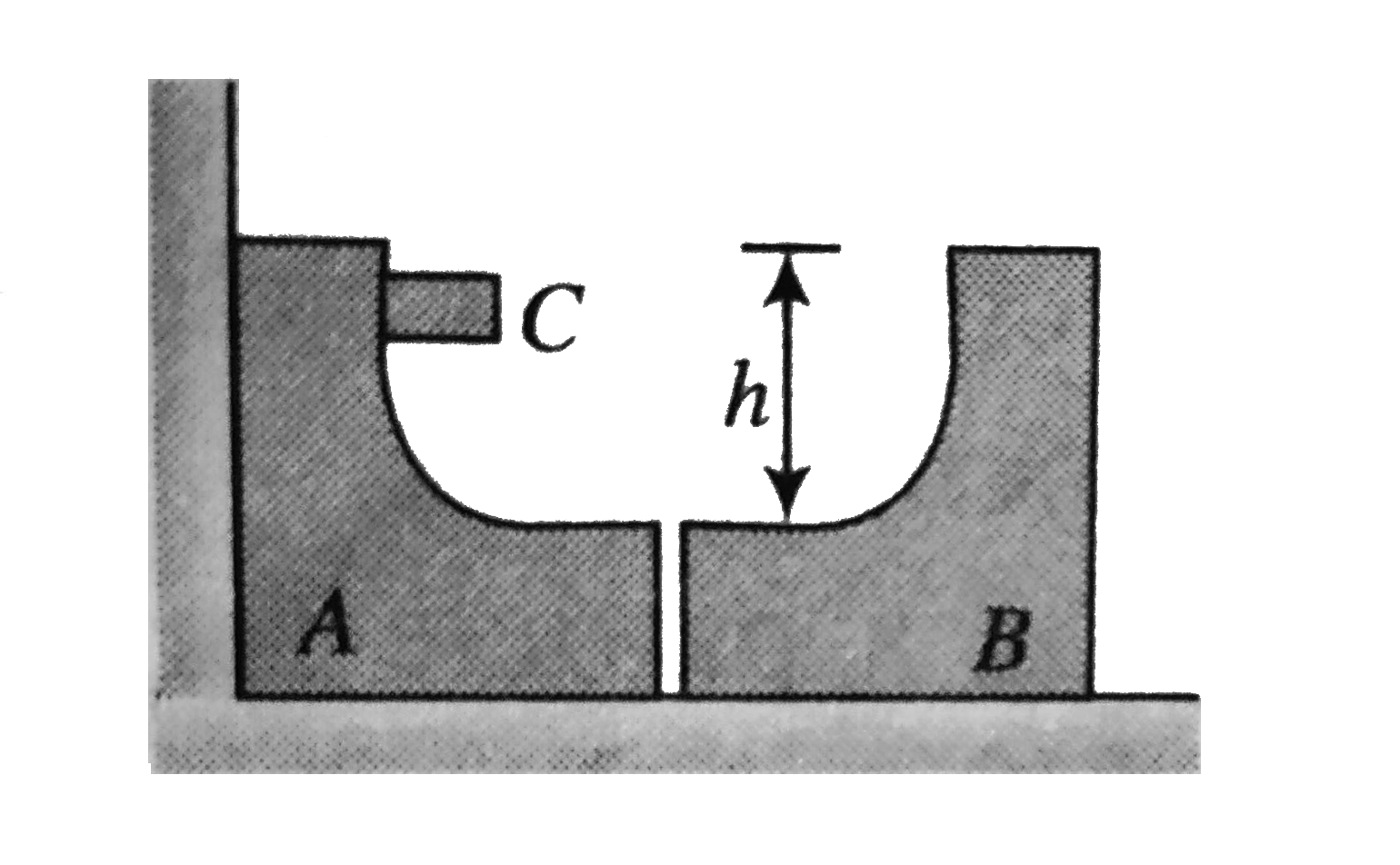 View Solution
View SolutionQuestion 228
A small sphere is given vertical velocity of magnitude v0=5ms−1 and it swings in a vertical plane about the end of a massless string. The angle θ with the vertical at which string will break, knowing that it can withstand a maximum tension equal to twice the weight of the sphere, is
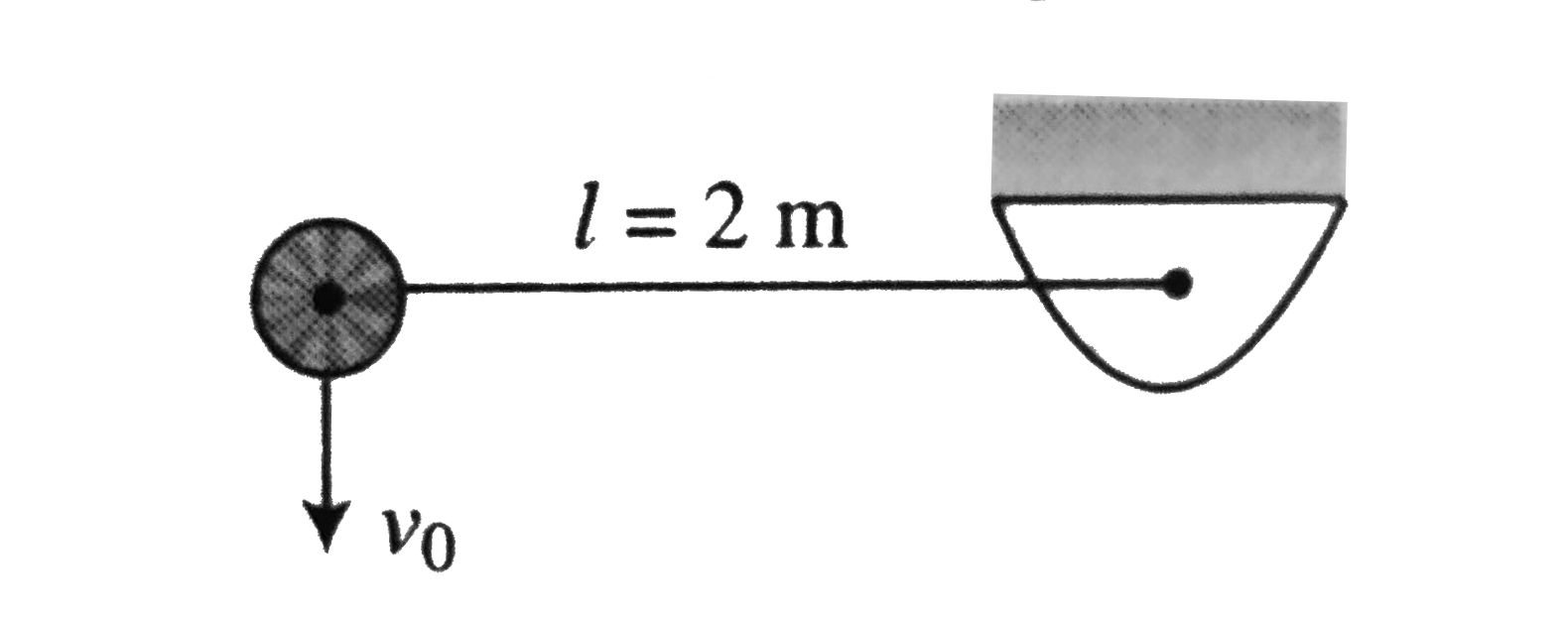 View Solution
View SolutionQuestion 230
A block of mass 5.0kg slides down from the top of an inclined plane of length 3m. The first 1m of the plane is smooth and the next 2m is rough. The block is released from rest and again comes to rest at the bottom of the plane. If the plane is inclined at 30∘ with the horizontal, find the coefficient of friction on the rough portion.
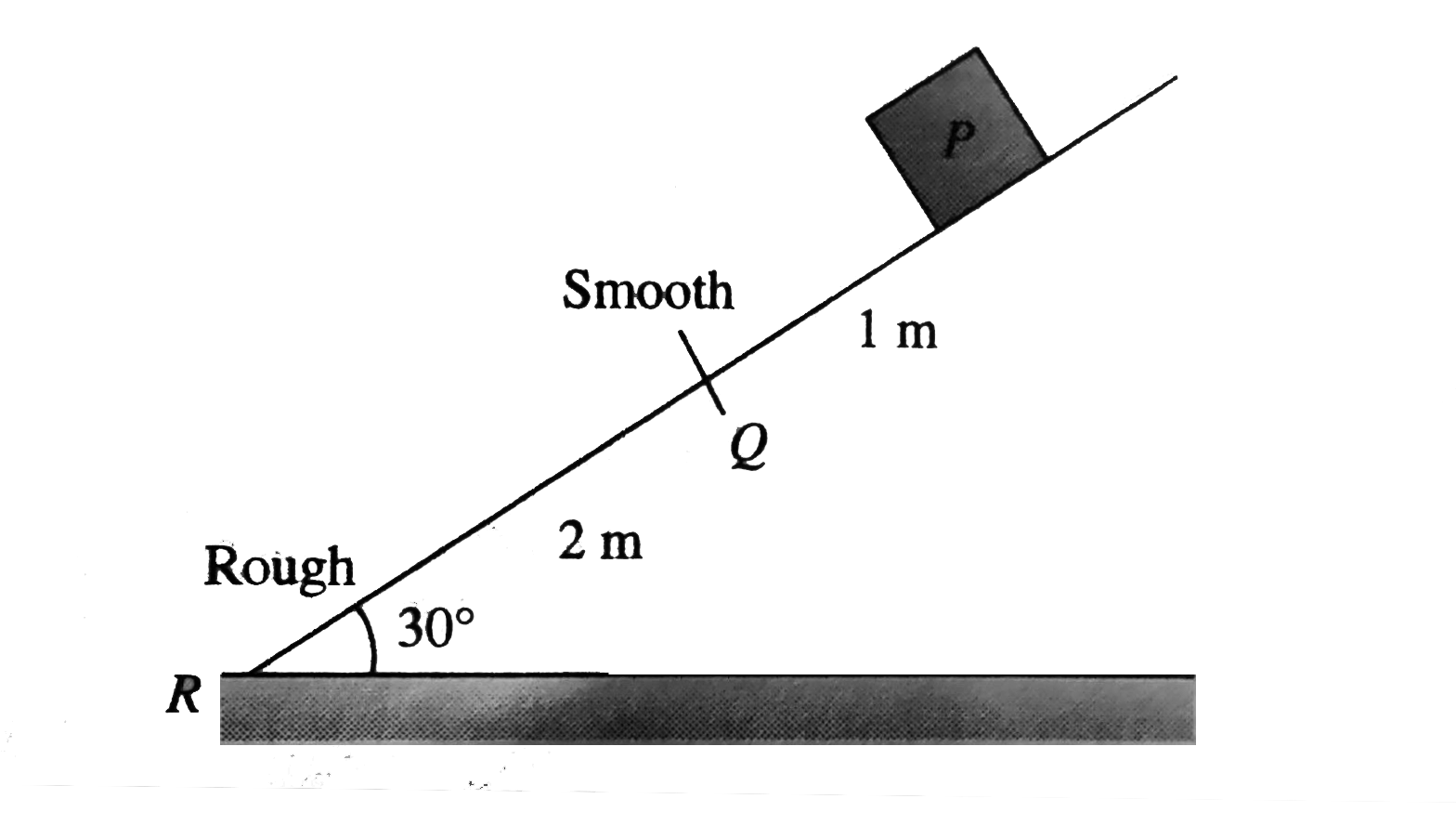 View Solution
View SolutionQuestion 241
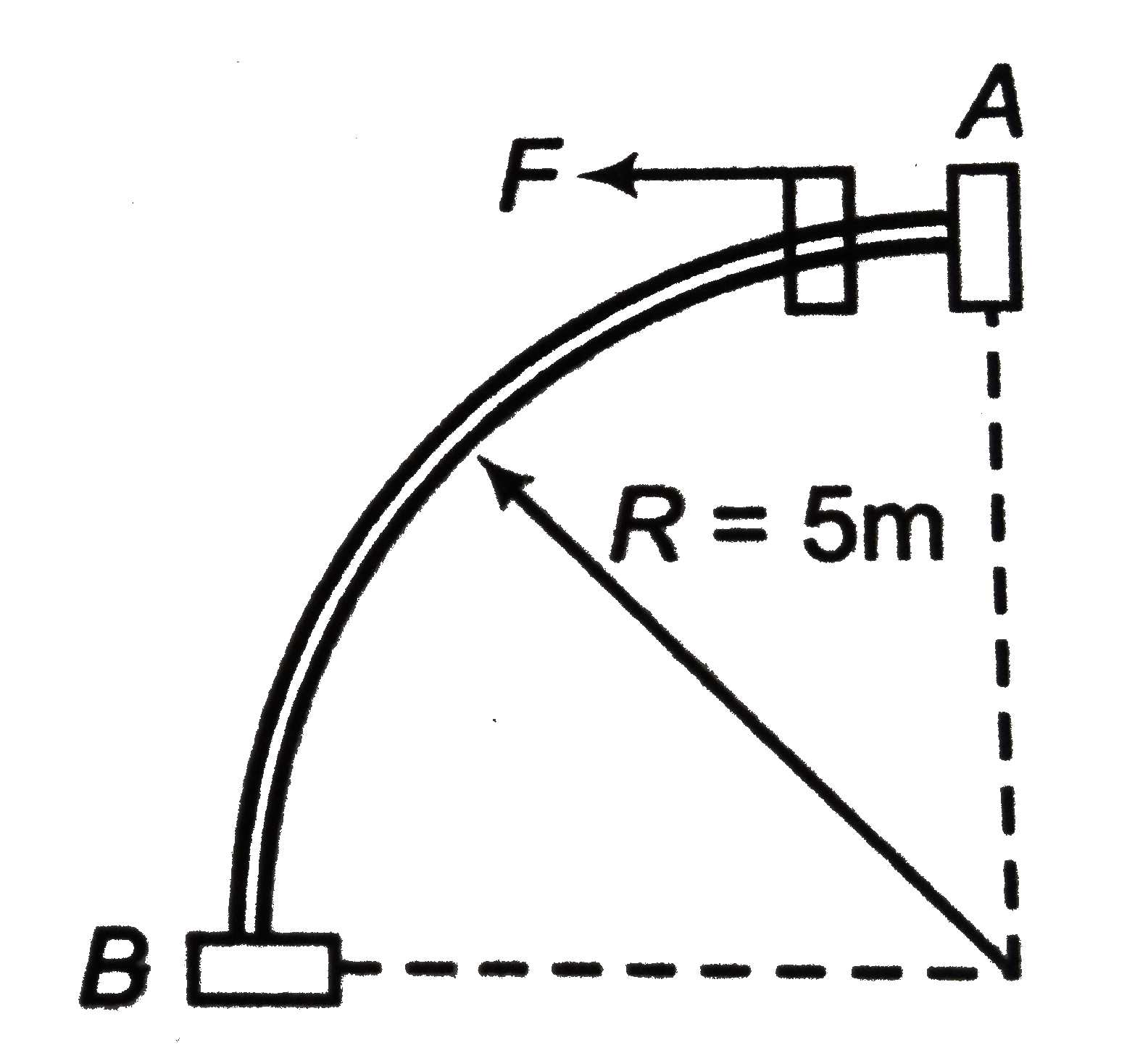
A vehicle is driven along a straight horizontal track by a motor which exerts a constant driving force. The vehicle starts from rest at t=0 and the effects of friction and air resistance are negligible. If the kinetic eneryg of the vehicle at time t is E and power developed by the motor is P, which of the following graphs are correct?View SolutionQuestion 247
A horizontal plane supports a plank with a block placed on it. A light elastic string is attached to the block, which is attached to a fixed point O. Initially, the cord is unstretched and vertical. The plank is slowly shifted to right until the block starts sliding over it. It occurs at the moment when the cord deviates from vertical by an angle θ=0∘. Work done by the force F equals
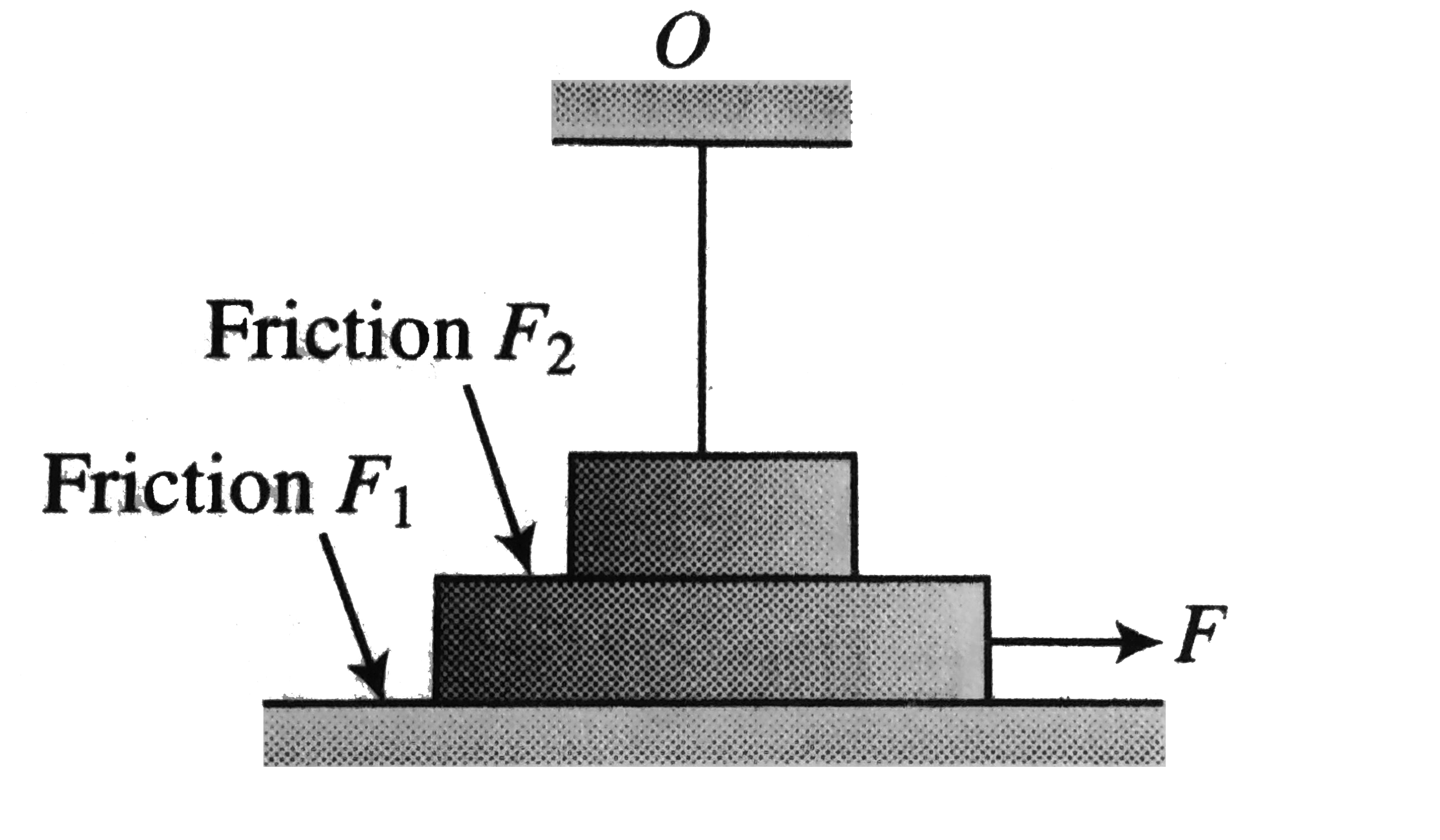 View Solution
View SolutionQuestion 253
A particle is taken from point A to point B under the influence of a force field. Now it is taken back from B to A and it is observed that the work done in taking the particle from A to B is not equal to the work done in taking it from B to A. If Wnc and Wc are the work done by non-conservative and conservative forces present in the system, respectively, ΔU is the change in potential energy and Δk is the change in kinetic energy, thenView SolutionQuestion 268
A single conservative force F(x) acts on a on a (1.0kg ) particle that moves along the x-axis. The potential energy U(x) is given by:
U(x)=20+(x−2)2
where, x is meters. At x=5.0m the particle has a kinetic energy of 20J
(a) What is the mechanical energy of the system?
(b) Make a plot of U(x) as a function of x for −10m≤x≤10m, and on the same graph draw the line that represents the mechanical energy of the system. Use part (b) to determine.
(c) The least value of x and
(d) the greatest value of x between which the particle can move.
(e) The maximum kinetic energy of the particle and
(f) the value of x at which it occurs.
(g) Datermine the equation for F(x) as a function of x.
(h) For what (finite ) value of x does F(x)=0?.View SolutionQuestion 269
A single conservative force F(x) acts on a on a (1.0kg ) particle that moves along the x-axis. The potential energy U(x) is given by:
U(x)=20+(x−2)2
where, x is meters. At x=5.0m the particle has a kinetic energy of 20J
(a) What is the mechanical energy of the system?
(b) Make a plot of U(x) as a function of x for −10m≤x≤10m, and on the same graph draw the line that represents the mechanical energy of the system. Use part (b) to determine.
(c) The least value of x and
(d) the greatest value of x between which the particle can move.
(e) The maximum kinetic energy of the particle and
(f) the value of x at which it occurs.
(g) Datermine the equation for F(x) as a function of x.
(h) For what (finite ) value of x does F(x)=0?.View SolutionQuestion 270
A single conservative force F(x) acts on a on a (1.0kg ) particle that moves along the x-axis. The potential energy U(x) is given by:
U(x)=20+(x−2)2
where, x is meters. At x=5.0m the particle has a kinetic energy of 20J
(a) What is the mechanical energy of the system?
(b) Make a plot of U(x) as a function of x for −10m≤x≤10m, and on the same graph draw the line that represents the mechanical energy of the system. Use part (b) to determine.
(c) The least value of x and
(d) the greatest value of x between which the particle can move.
(e) The maximum kinetic energy of the particle and
(f) the value of x at which it occurs.
(g) Datermine the equation for F(x) as a function of x.
(h) For what (finite ) value of x does F(x)=0?.View SolutionQuestion 271
A 1.5−kg block is initially at rest on a horizontal frictionless surface when a horizontal force in the positive direction of x-axis is applied to the block. The force is given by →F=(4−x2)→iN, where x is in meter and the initial position of the block is x=0.
The maximum kinetic energy of the block between x=0 and x=2.0m is
A.2.33 J B.8.67 J C.5.33 J D.6.67 JView SolutionQuestion 272
A 1.5−kg block is initially at rest on a horizontal frictionless surface when a horizontal force in the positive direction of x-axis is applied to the block. The force is given by →F=(4−x2)→iN, where x is in meter and the initial position of the block is x=0.
The maximum kinetic energy of the block between x=0 and x=2.0m is
A.2.33 J B.8.67 J C.5.33 J D.6.67 JView SolutionQuestion 278
A man of mass m speeds up while running from rest to a speed v in a straight track along an inclined plane, after raising through a height h.
Wgravity=work done by gravity on the man
Wiction=work done by friction on the man
Wman=work done by man
Which of the following options is correct regarding the various work done?View SolutionQuestion 279
A man of mass m speeds up while running from rest to a speed v in a straight track along an inclined plane, after raising through a height h.
Wgravity=work done by gravity on the man
Wiction=work done by friction on the man
Wman=work done by man
If instead of moving up the plane, the man increases his speed to the value v while moving down the inclined plane through the same vertical distance h, thenView SolutionQuestion 280
A man of mass m speeds up while running from rest to a speed v in a straight track along an inclined plane, after raising through a height h.
Wgravity=work done by gravity on the man
Wiction=work done by friction on the man
Wman=work done by man
If in the previous problem, we replace the man by a block of mass m and release it from top of the inclined plane, and let it gain a speed v, thenView SolutionQuestion 281
A boy of mass m climbs up a conveyor belt with a constant acceleration. The speed of the belt is v=√gh/6 and the coefficient of friction between the body and conveyor belt is μ=53√3. The boy starts from A and moves with the maximum possible acceleration till he reaches the highest point B.
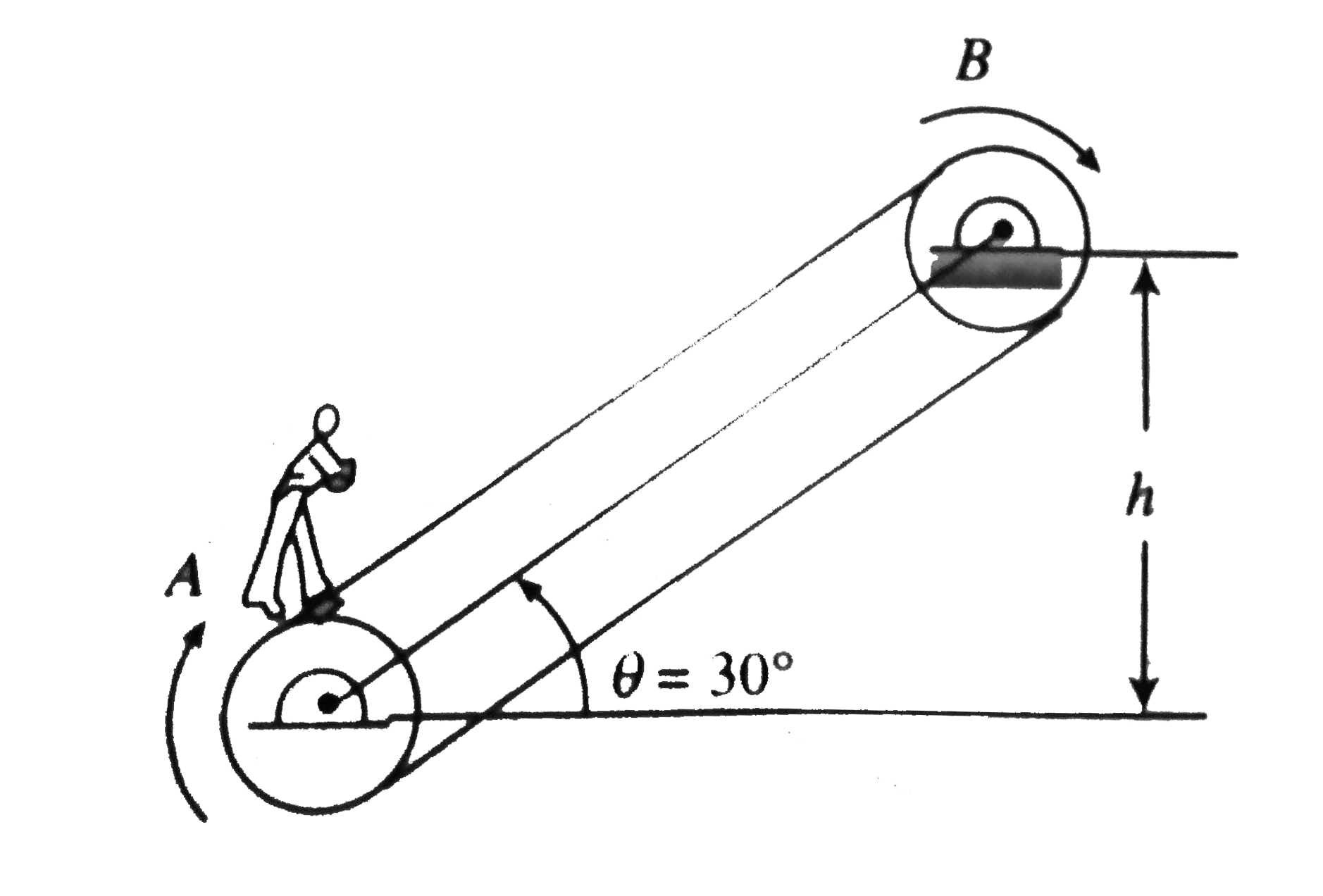
The time taken by the boy to reach the height h is View SolutionQuestion 282
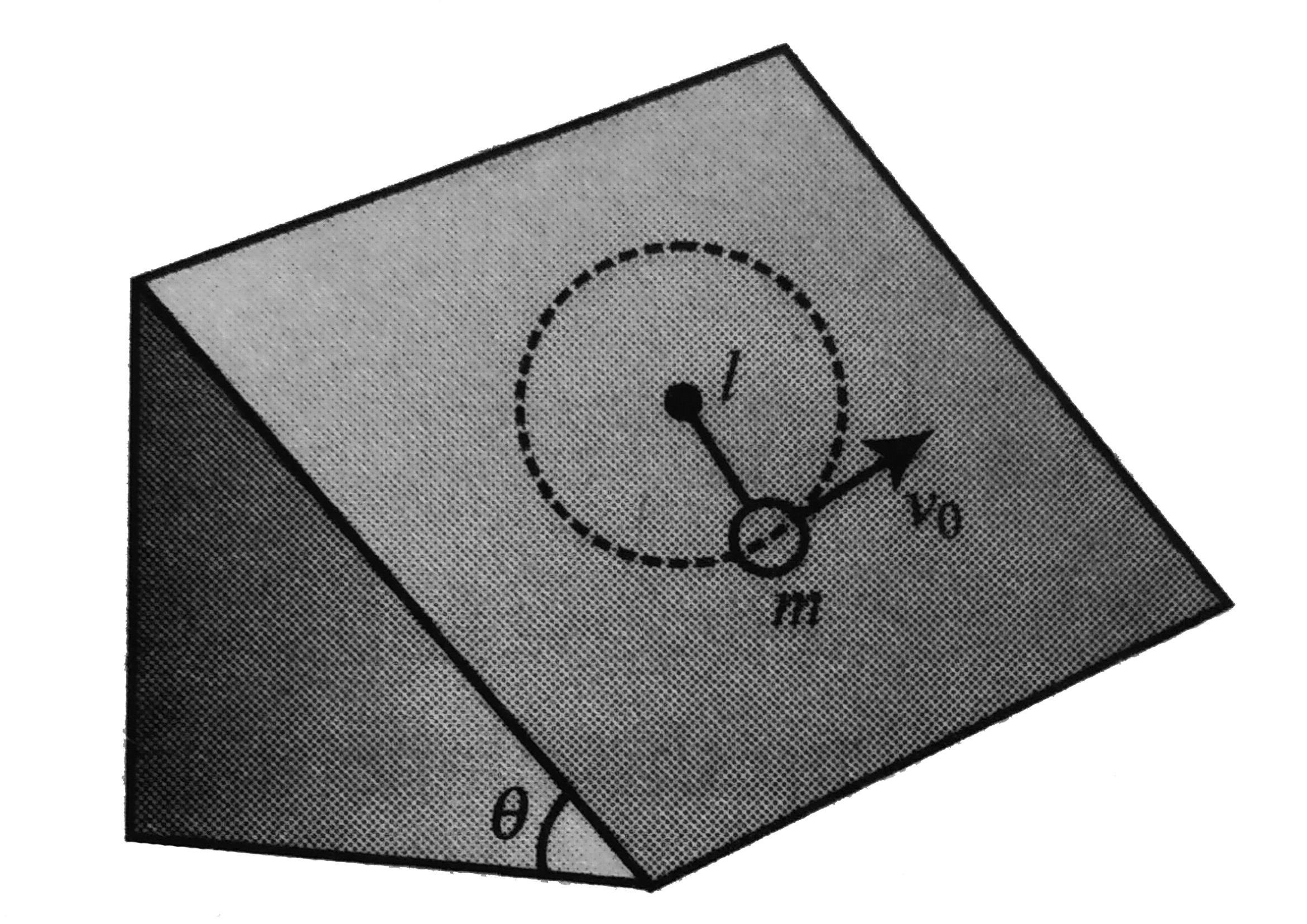
A boy of mass m climbs up a conveyor belt with a constant acceleration. The speed of the belt is v=√gh/6 and the coefficient of friction between the body and conveyor belt is μ=53√3. The boy starts from A and moves with the maximum possible acceleration till he reaches the highest point B.
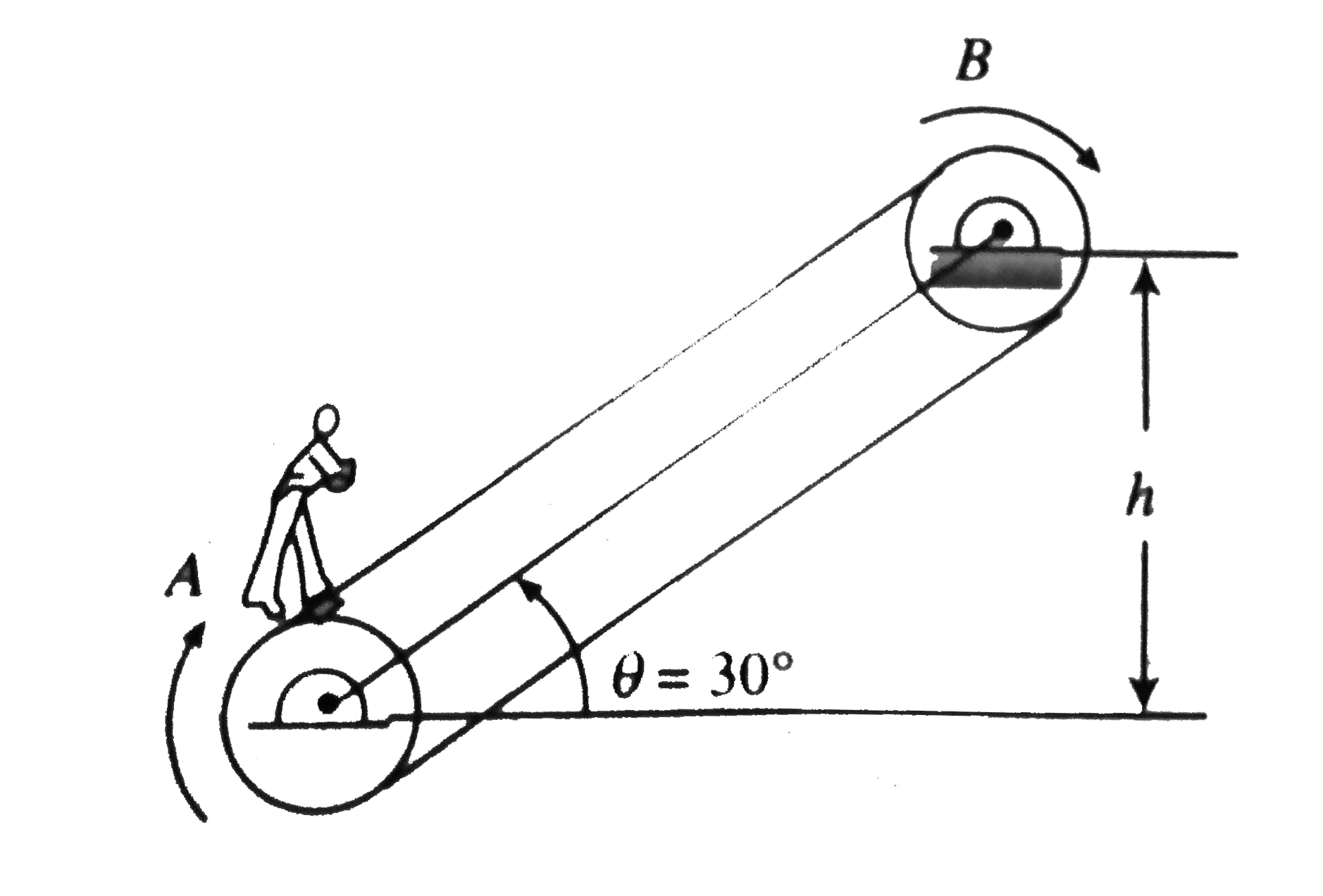
Work done by gravity to w.r.t. the conveyor belt isView SolutionQuestion 283
A boy of mass m climbs up a conveyor belt with a constant acceleration. The speed of the belt is v=√gh/6 and the coefficient of friction between the body and conveyor belt is μ=53√3. The boy starts from A and moves with the maximum possible acceleration till he reaches the highest point B.
Work done by the boy is View SolutionQuestion 284
A boy of mass m climbs up a conveyor belt with a constant acceleration. The speed of the belt is v=√gh/6 and the coefficient of friction between the body and conveyor belt is μ=53√3. The boy starts from A and moves with the maximum possible acceleration till he reaches the highest point B.

Work done by the boy is View SolutionQuestion 285
Ram and Ali have been fast friends since childhood. Ali neglected studies and now has no means to earn money other than a channel whereas Ram has become an engineer. Now both are working in the same factory. Ali uses camel to transport the load within the factory.
 Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
i. The load used in each trip is 1000kg and has friction coefficient μk=0.1 and μs=0.2.
ii. Mass of camel is 500kg.
iii. Load is accelerated for first 50m with constant acceleration, then it is pulled at a constant speed of 5ms−1 for 2km and at last stopped with constant retardation in 50m.
iv. From biological data, the rate of consumption of energy of camel can be expressed as P=18×103v+104Js−1 where P is the power and v is the velocity of the camel. After calculations on different issues, Ram suggested proper food, speed of camel, etc. to his friend. For the welfare of Ali, Ram wrote a letter to the management to increase his salary.
(Assuming that the camel exerts a horizontal force on the load):
Sign of work done by the camel on the load during parts of motion, accelerated motion, uniform motion and retarded motion, respectively areView SolutionQuestion 286
Ram and Ali have been fast friends since childhood. Ali neglected studies and now has no means to earn money other than a channel whereas Ram has become an engineer. Now both are working in the same factory. Ali uses camel to transport the load within the factory.
 Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
i. The load used in each trip is 1000kg and has friction coefficient μk=0.1 and μs=0.2.
ii. Mass of camel is 500kg.
iii. Load is accelerated for first 50m with constant acceleration, then it is pulled at a constant speed of 5ms−1 for 2km and at last stopped with constant retardation in 50m.
iv. From biological data, the rate of consumption of energy of camel can be expressed as P=18×103v+104Js−1 where P is the power and v is the velocity of the camel. After calculations on different issues, Ram suggested proper food, speed of camel, etc. to his friend. For the welfare of Ali, Ram wrote a letter to the management to increase his salary.
(Assuming that the camel exerts a horizontal force on the load):
Maximum power transmitted by the camel to load isView SolutionQuestion 287
Ram and Ali have been fast friends since childhood. Ali neglected studies and now has no means to earn money other than a channel whereas Ram has become an engineer. Now both are working in the same factory. Ali uses camel to transport the load within the factory.
 Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
i. The load used in each trip is 1000kg and has friction coefficient μk=0.1 and μs=0.2.
ii. Mass of camel is 500kg.
iii. Load is accelerated for first 50m with constant acceleration, then it is pulled at a constant speed of 5ms−1 for 2km and at last stopped with constant retardation in 50m.
iv. From biological data, the rate of consumption of energy of camel can be expressed as P=18×103v+104Js−1 where P is the power and v is the velocity of the camel. After calculations on different issues, Ram suggested proper food, speed of camel, etc. to his friend. For the welfare of Ali, Ram wrote a letter to the management to increase his salary.
(Assuming that the camel exerts a horizontal force on the load):
Maximum power transmitted by the camel to load isView SolutionQuestion 288
Ram and Ali have been fast friends since childhood. Ali neglected studies and now has no means to earn money other than a channel whereas Ram has become an engineer. Now both are working in the same factory. Ali uses camel to transport the load within the factory.
 Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
i. The load used in each trip is 1000kg and has friction coefficient μk=0.1 and μs=0.2.
ii. Mass of camel is 500kg.
iii. Load is accelerated for first 50m with constant acceleration, then it is pulled at a constant speed of 5ms−1 for 2km and at last stopped with constant retardation in 50m.
iv. From biological data, the rate of consumption of energy of camel can be expressed as P=18×103v+104Js−1 where P is the power and v is the velocity of the camel. After calculations on different issues, Ram suggested proper food, speed of camel, etc. to his friend. For the welfare of Ali, Ram wrote a letter to the management to increase his salary.
(Assuming that the camel exerts a horizontal force on the load):
The ratio of the energy consumed by the camel during uniform motion for the two cases when it moves with speed 5ms−1 to the case when it moves with 10ms−1 View SolutionQuestion 289
Ram and Ali have been fast friends since childhood. Ali neglected studies and now has no means to earn money other than a channel whereas Ram has become an engineer. Now both are working in the same factory. Ali uses camel to transport the load within the factory.
 Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
i. The load used in each trip is 1000kg and has friction coefficient μk=0.1 and μs=0.2.
ii. Mass of camel is 500kg.
iii. Load is accelerated for first 50m with constant acceleration, then it is pulled at a constant speed of 5ms−1 for 2km and at last stopped with constant retardation in 50m.
iv. From biological data, the rate of consumption of energy of camel can be expressed as P=18×103v+104Js−1 where P is the power and v is the velocity of the camel. After calculations on different issues, Ram suggested proper food, speed of camel, etc. to his friend. For the welfare of Ali, Ram wrote a letter to the management to increase his salary.
(Assuming that the camel exerts a horizontal force on the load):
Maximum power transmitted by the camel to load isView SolutionQuestion 290
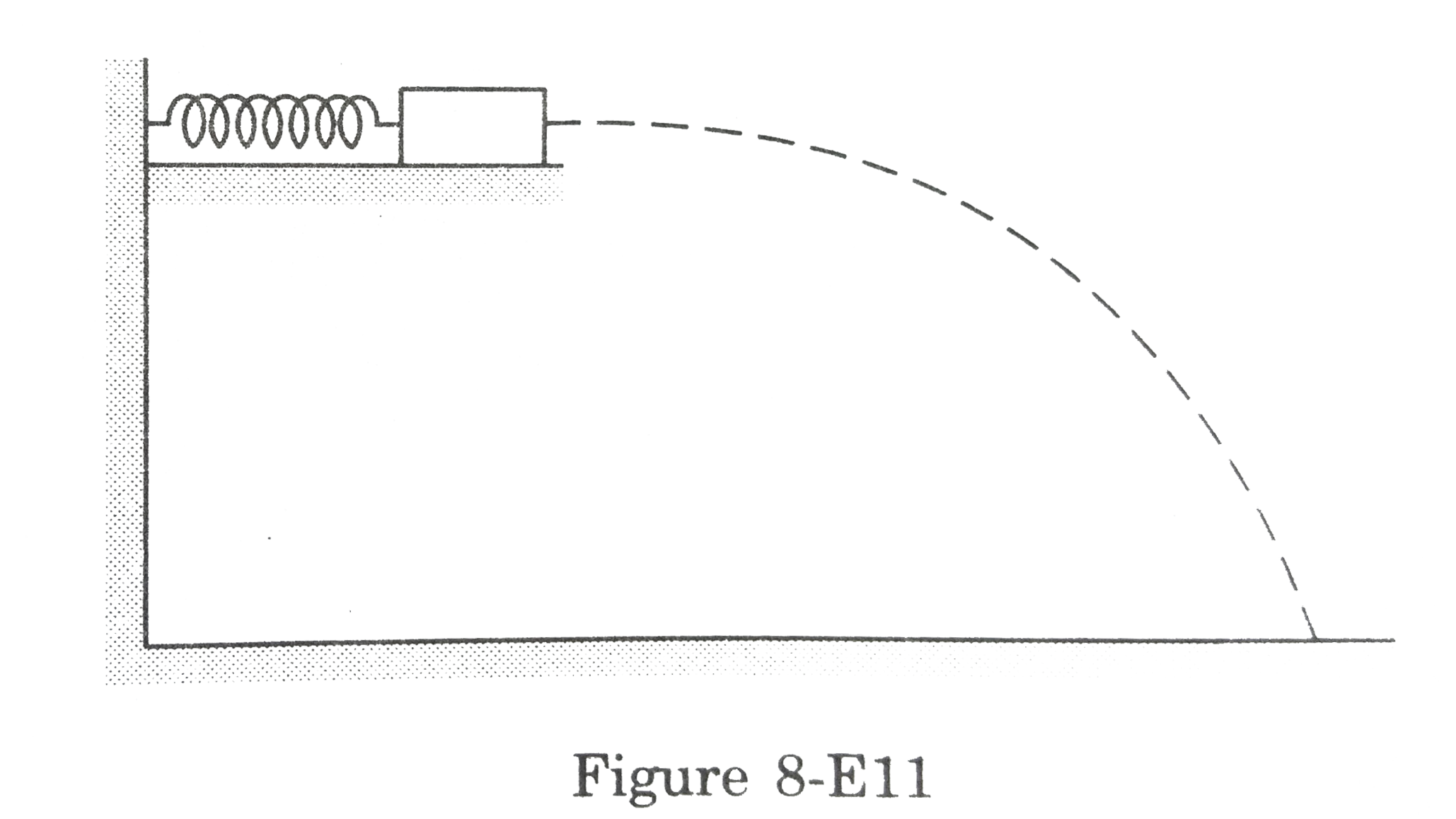
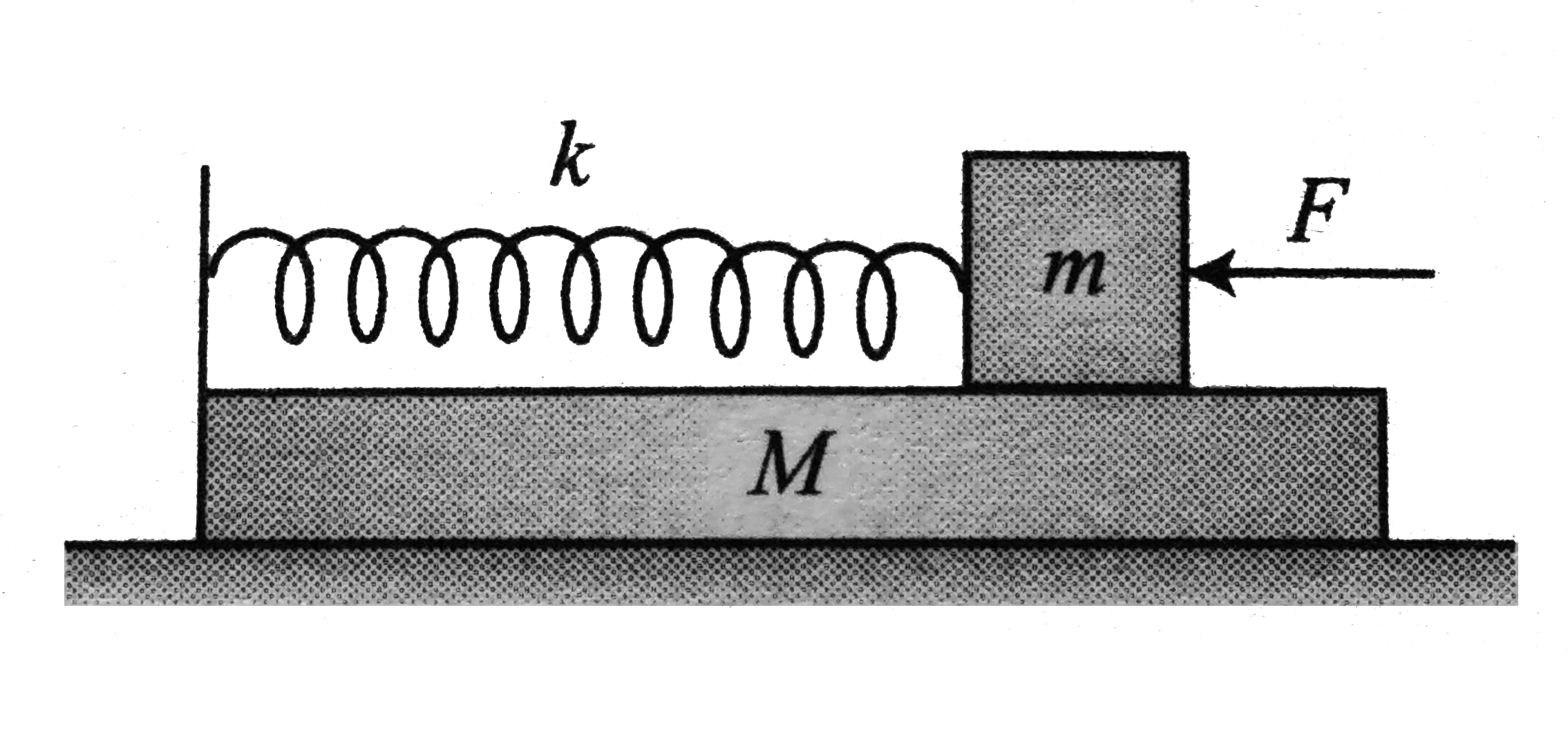
A srping lies along the x-axis attached to a wall at one end and a block at the other end. The block rests on a friction less surface at x=0. A force of constant magnitude F is applied to the block that begins to compress the spring, until the block comes to a maximum displacement xmax.
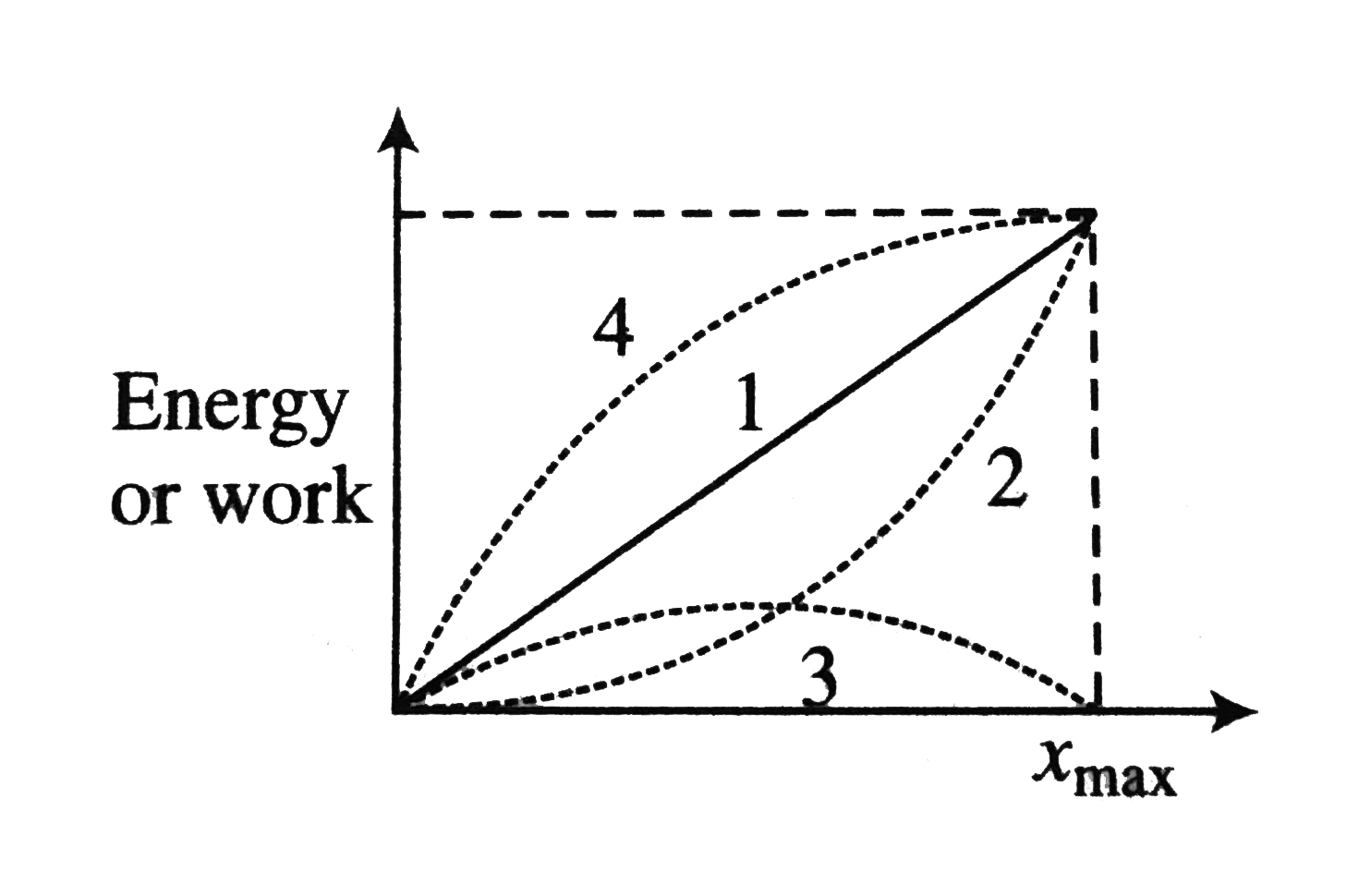
During the displacement, which of the curves shown in the graph best represents the kinetic energy of the block?View SolutionQuestion 291
A srping lies along the x-axis attached to a wall at one end and a block at the other end. The block rests on a friction less surface at x=0. A force of constant magnitude F is applied to the block that begins to compress the spring, until the block comes to a maximum displacement xmax.
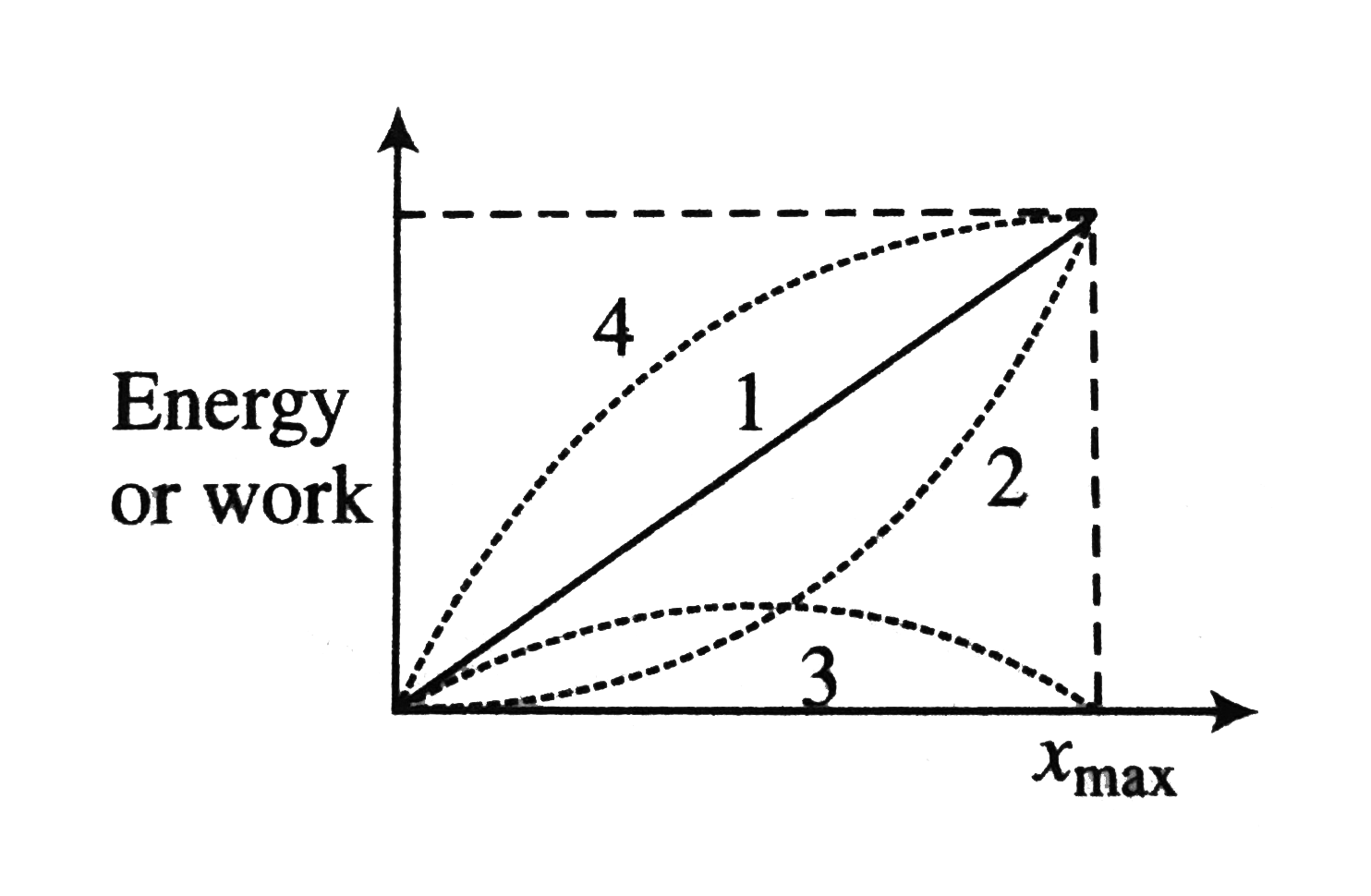
During the displacement, which of the curves shown in the graph best represents the work done on the spring block system by the applied force?View SolutionQuestion 292
A srping lies along the x-axis attached to a wall at one end and a block at the other end. The block rests on a friction less surface at x=0. A force of constant magnitude F is applied to the block that begins to compress the spring, until the block comes to a maximum displacement xmax.
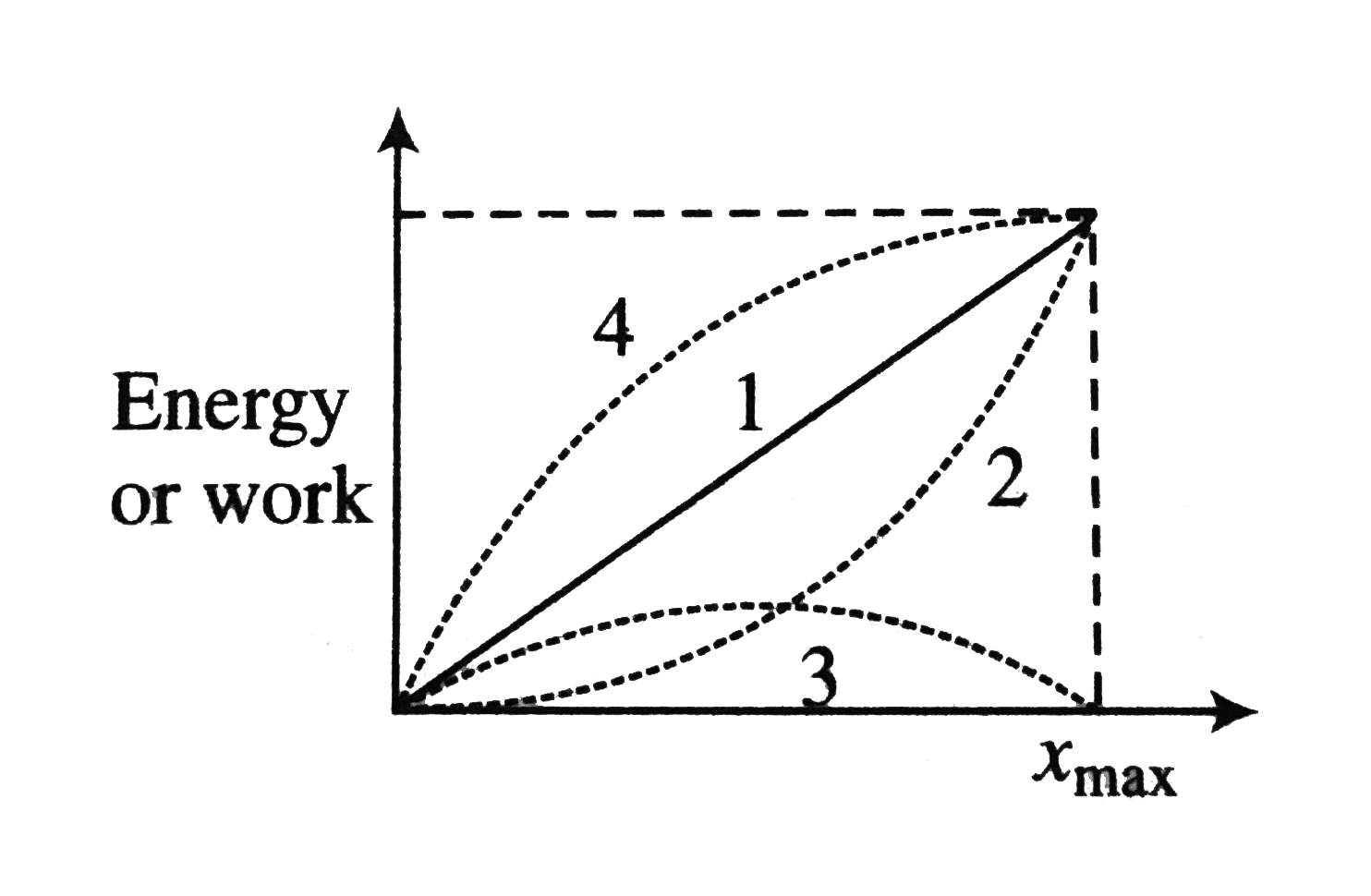
During the first half of the motion, applied force transfers more energy to theView SolutionQuestion 293
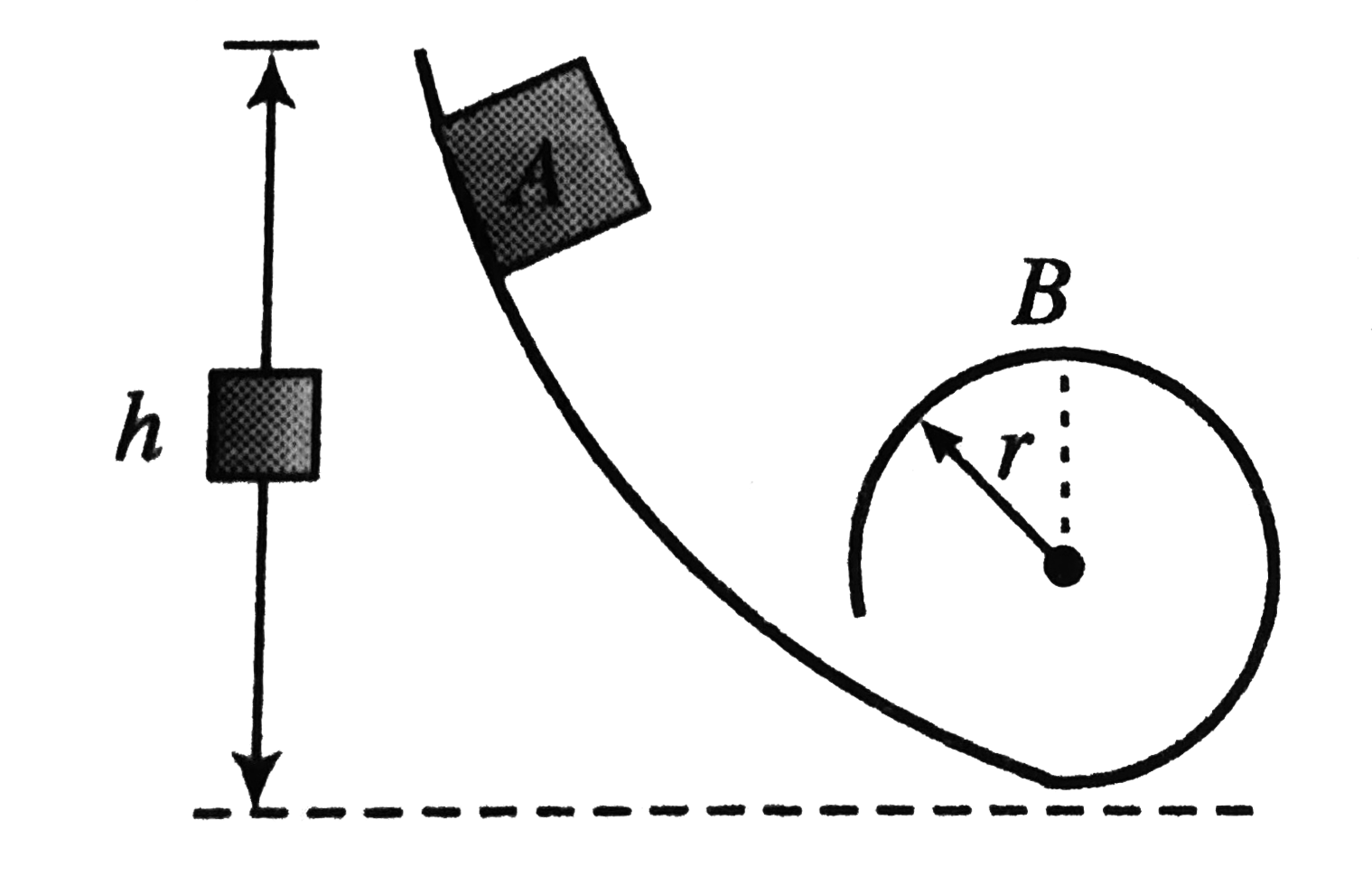
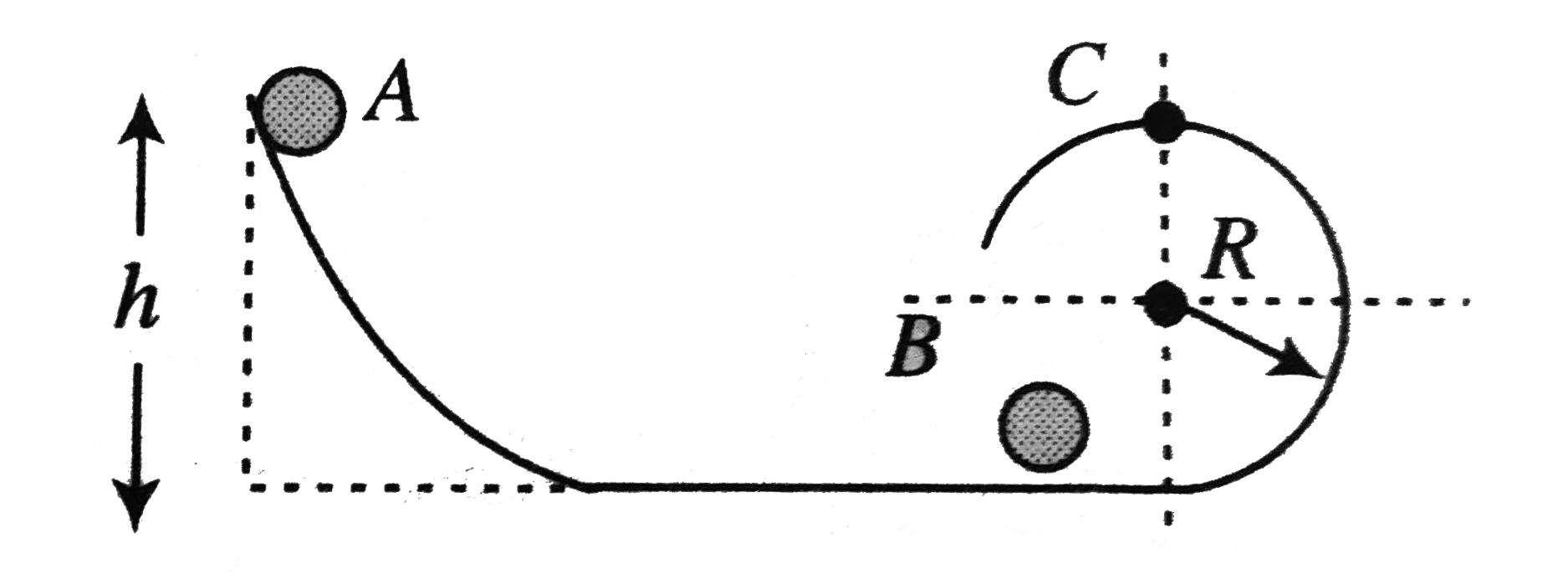
A small ball is given some velocity at point A towards right so that it moves on the semicircular track and does not leave contact up to the highest point B. After leaving the highest point B, it falls at the top of a building of height R and width x(x<<2R). (All the surfaces are frictionless).
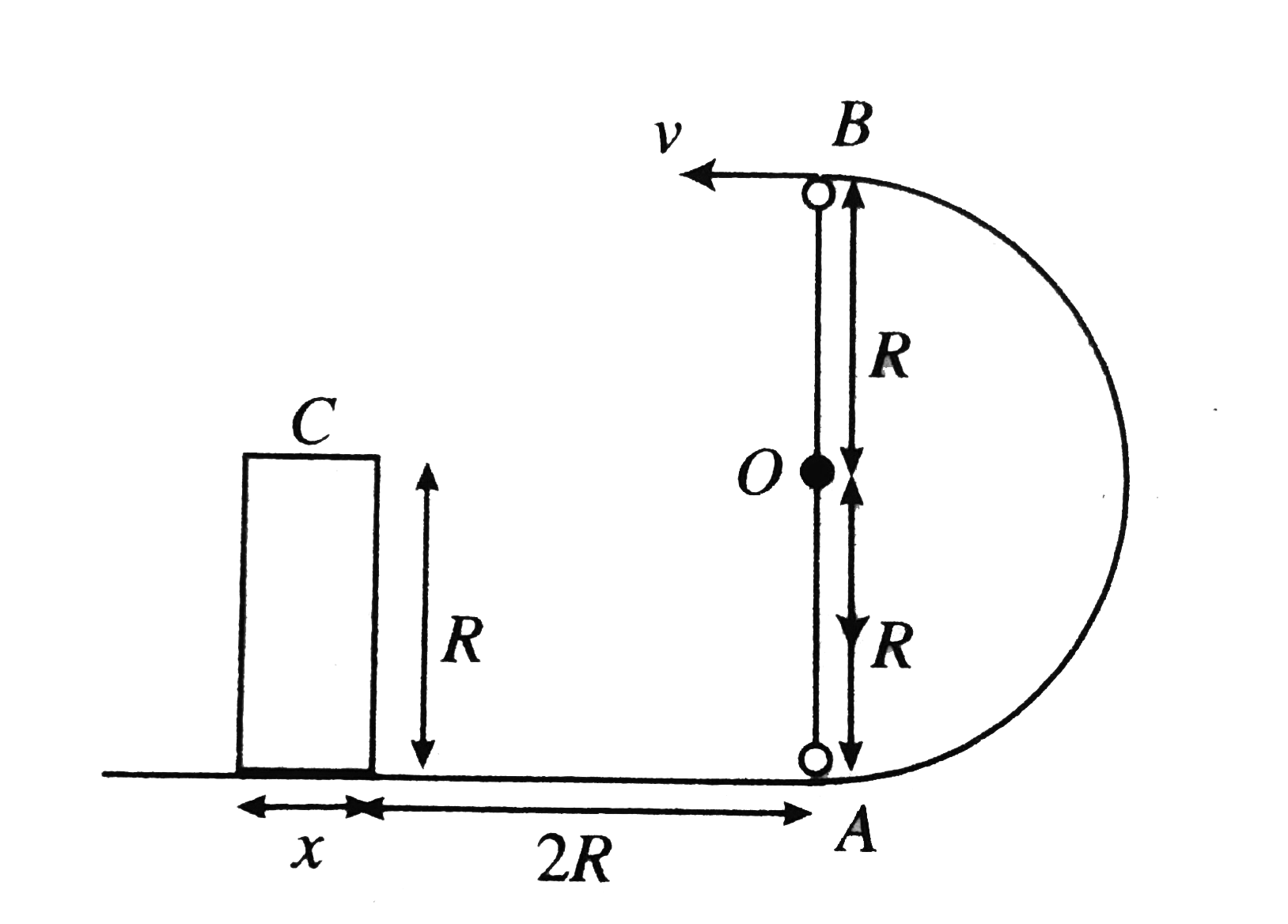
The velocity given to the ball at point A so that it may hit the top of the building is View SolutionQuestion 294
A small ball is given some velocity at point A towards right so that it moves on the semicircular track and does not leave contact up to the highest point B. After leaving the highest point B, it falls at the top of a building of height R and width x(x<<2R). (All the surfaces are frictionless).
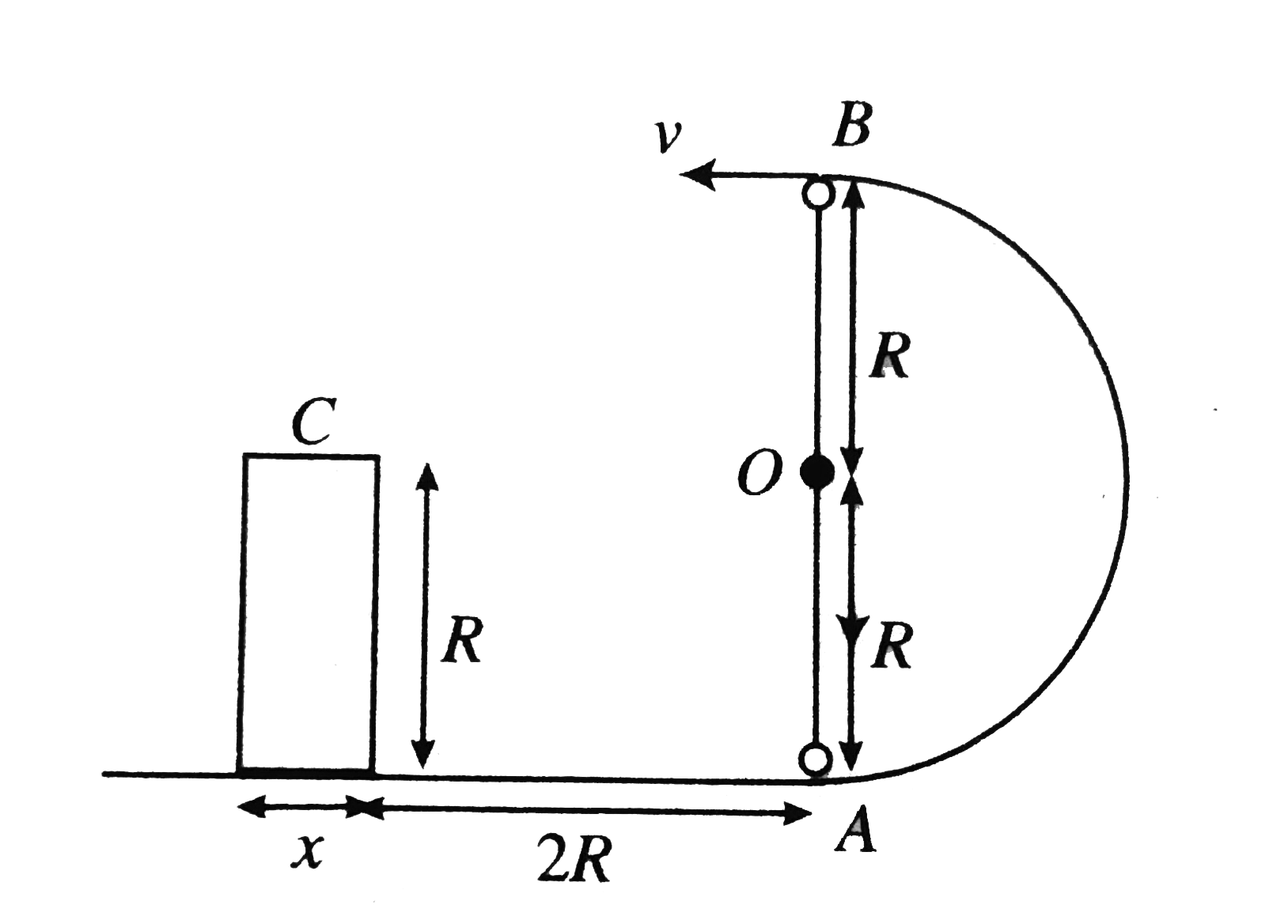
If the collision of ball with the building is elastic, then the angle with the horizontal at which the ball will rebound from the top of the building is View SolutionQuestion 295
A small ball is given some velocity at point A towards right so that it moves on the semicircular track and does not leave contact up to the highest point B. After leaving the highest point B, it falls at the top of a building of height R and width x(x<<2R). (All the surfaces are frictionless).
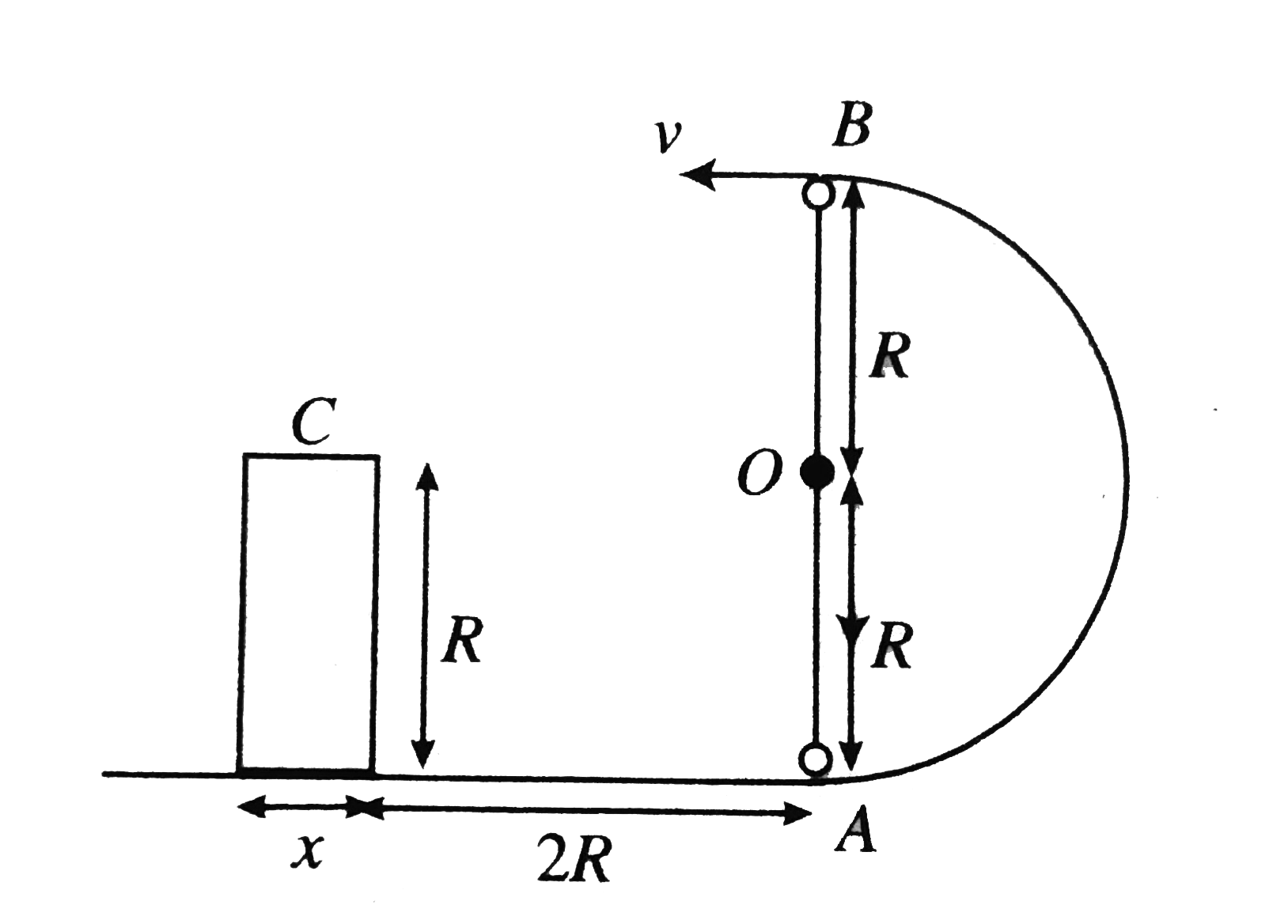
The horizontal distance of the ball from the foot of the builing where the ball strikes the horizontal ground will View SolutionQuestion 296
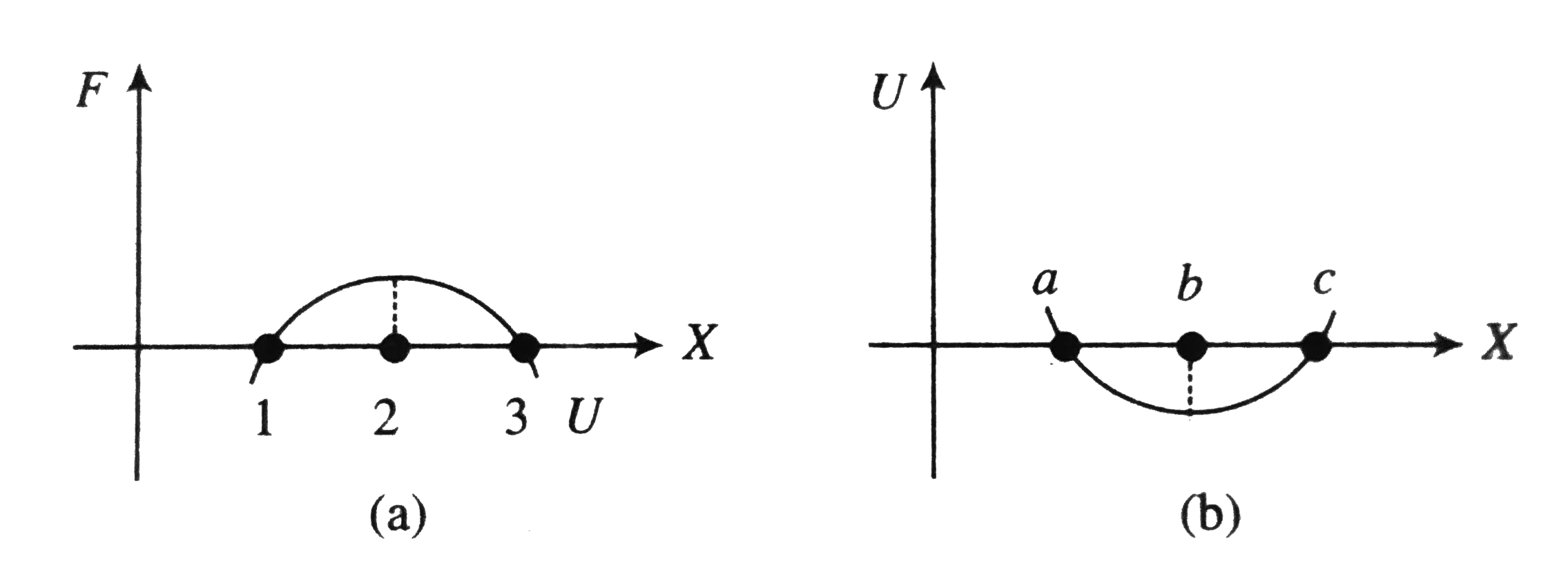
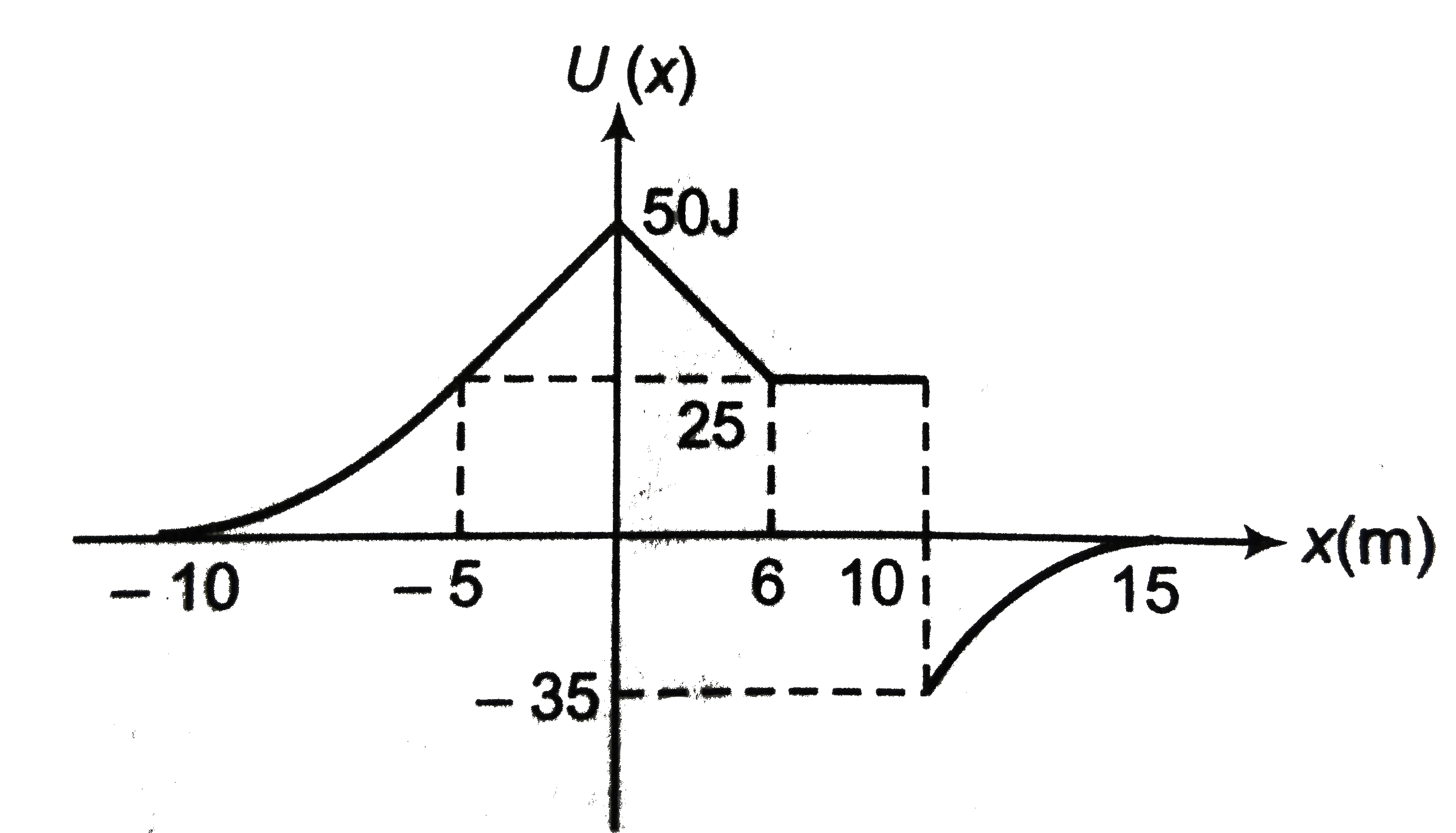
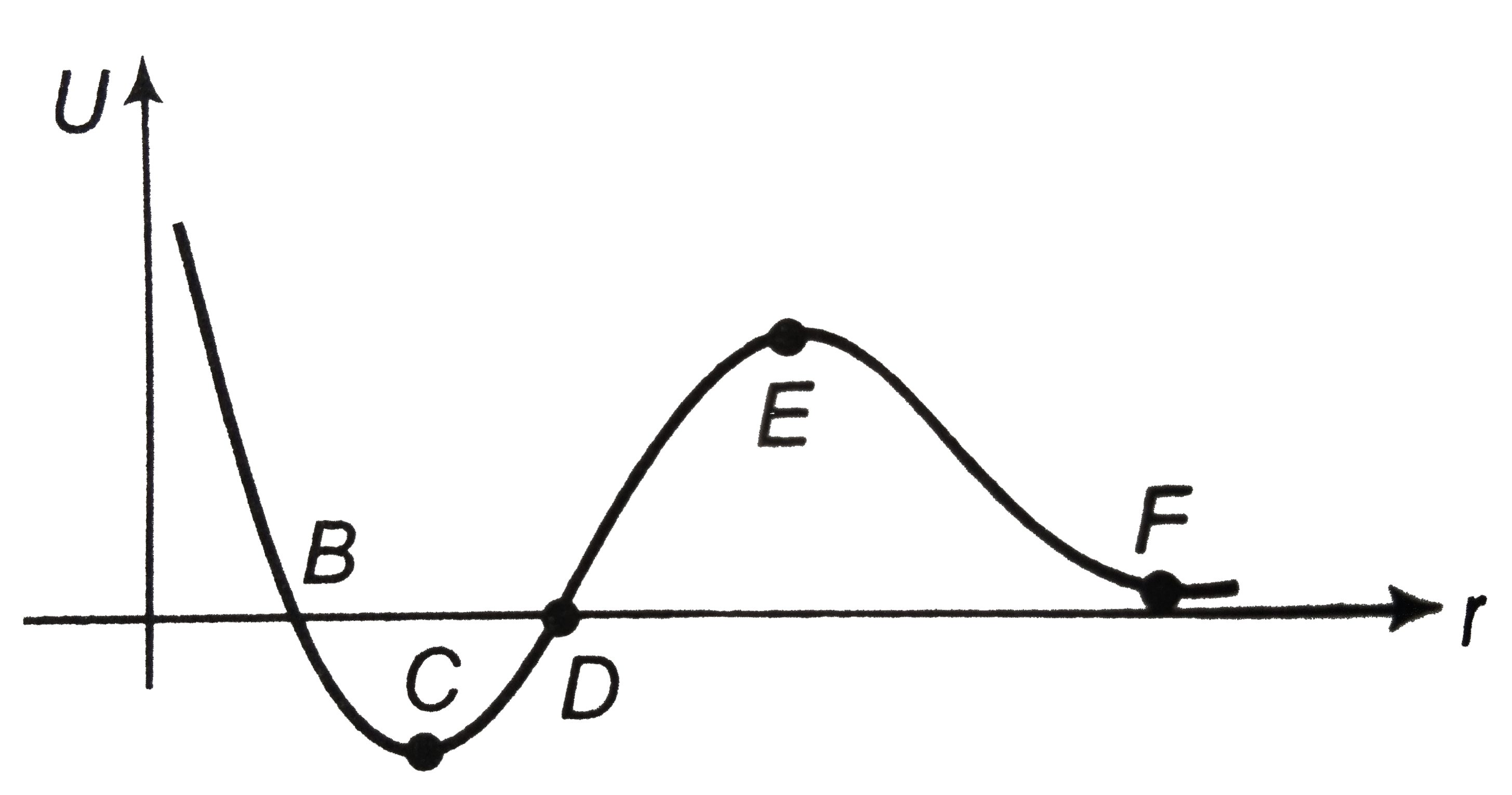
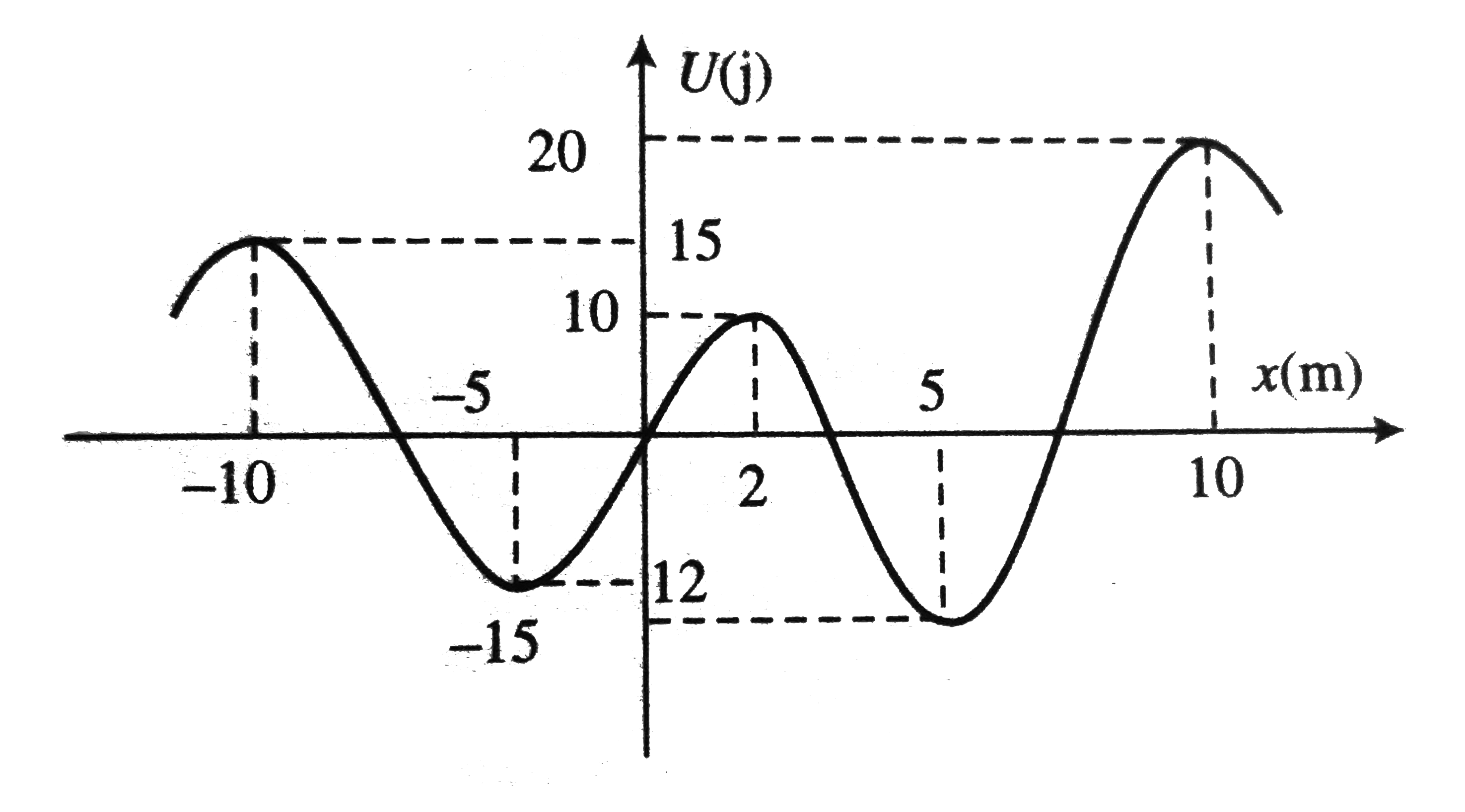
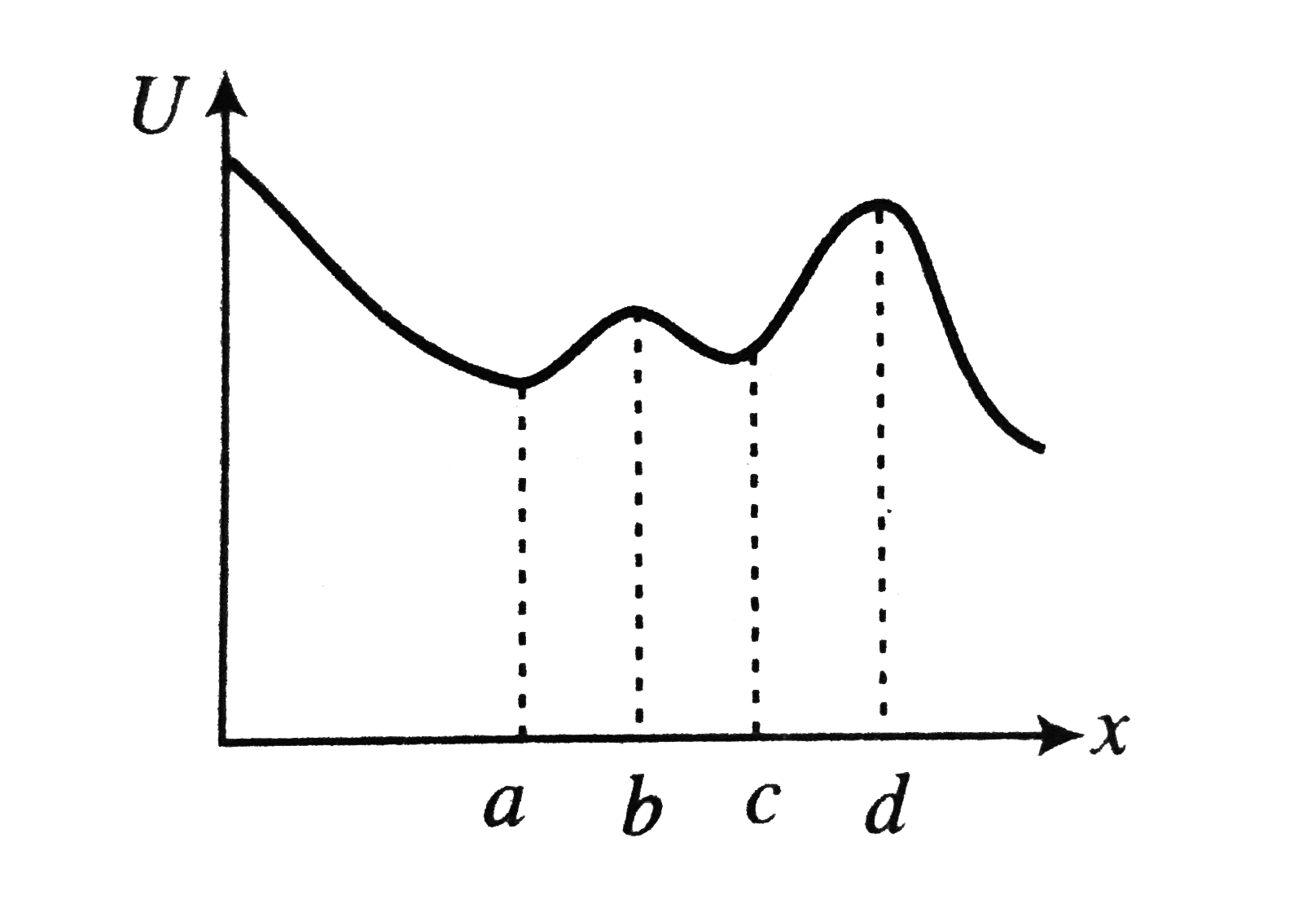
The figure shows the variation of potential energy of a particle as a function pf x, the x-coordination of the region. It has been assumed that potential energy depends only on x. For all other values x,U is zero. i.e. forx<−10 and x>15,U=0.
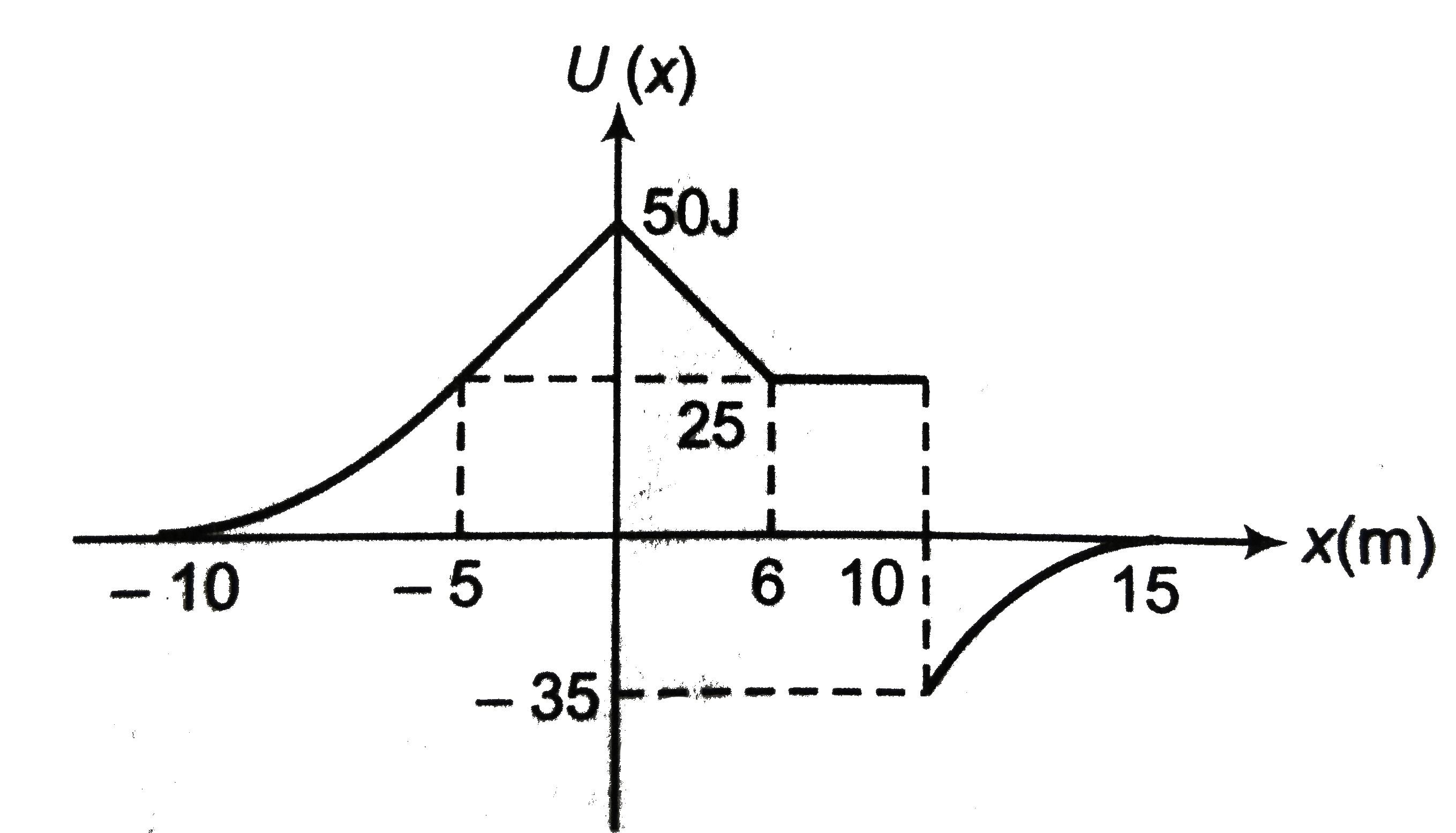
If total mechanical energy of the particle is 25J, then it can found in the region View SolutionQuestion 297
The figure shows the variation of potential energy of a particle as a funcation of x, the x-coordinate of the region. It has been assumed that potential energy depends only on x. For all other values x,U is zero. i.e. forx<−10 and x>15,U=0.
If total mechanical energy of the particle is −40J, then it can be found in region.View SolutionQuestion 298
Figure shows the variation of potential energy of a particle as a function of x, the x-coordinate of the region. It has been assumed that potential energy depends only on x. For all other values of x, U is zero, i.e., x←10 and x>15, U=0.
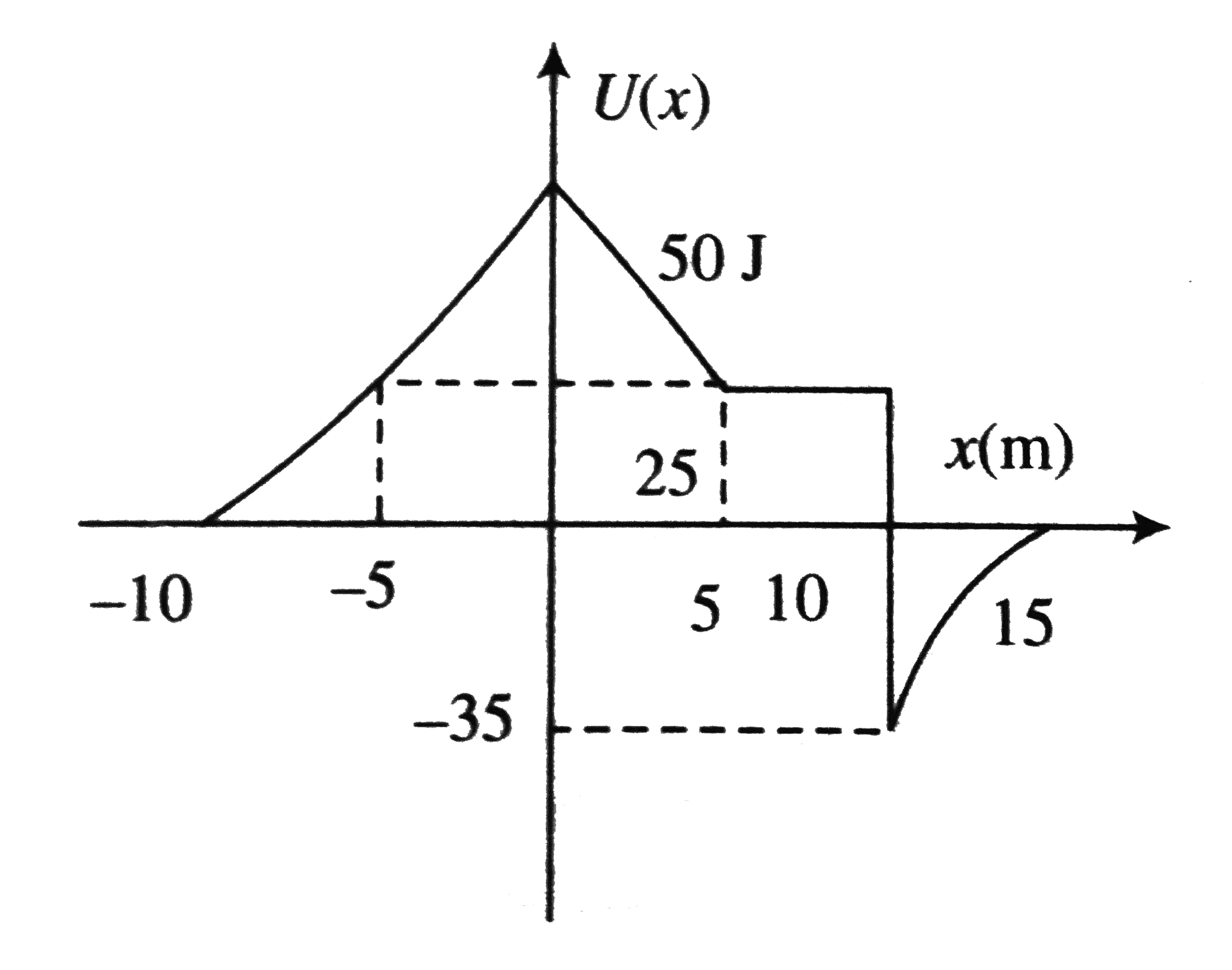
If the particle is isolated and its total mechanical energy is 60J, thenView SolutionQuestion 299
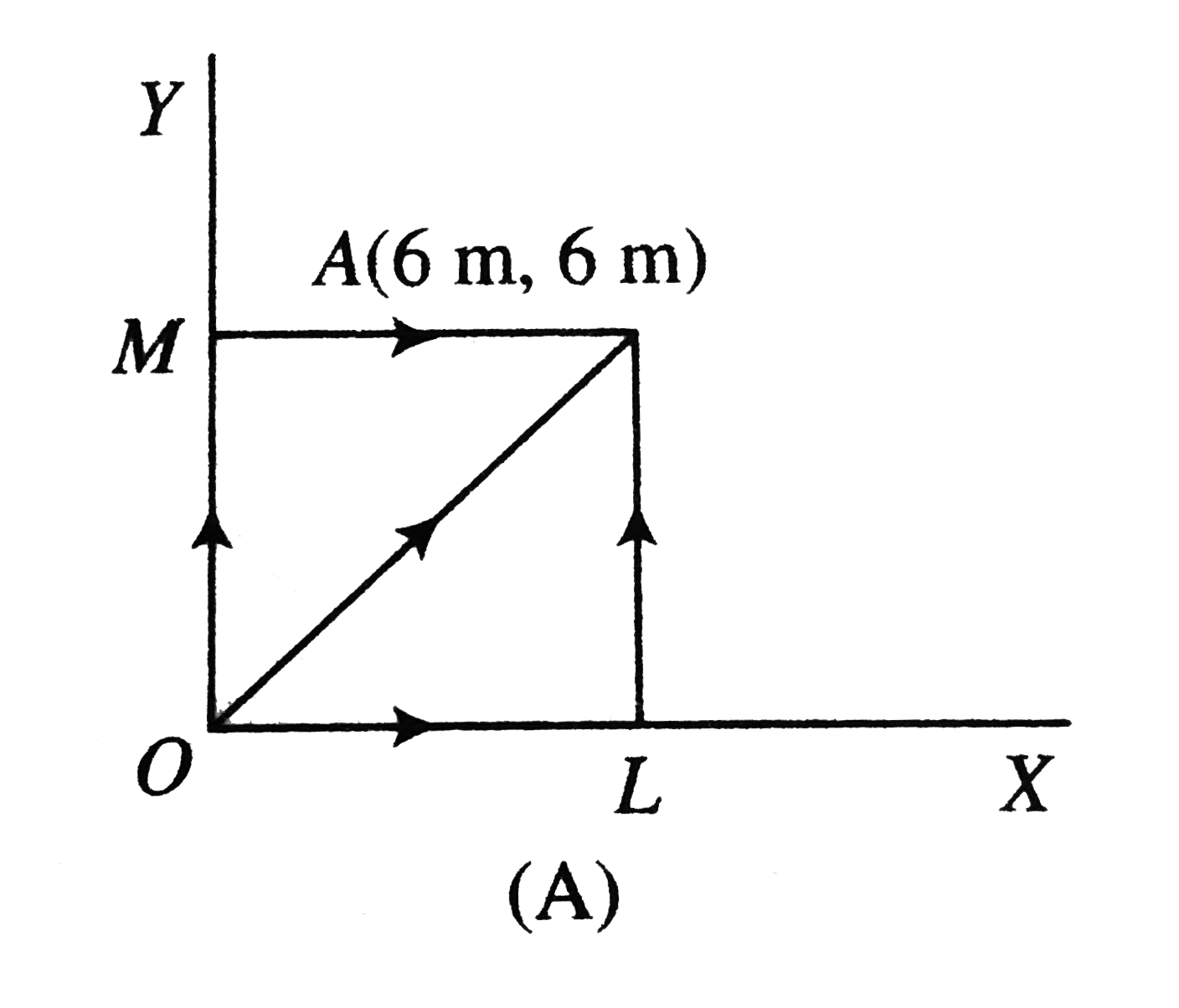
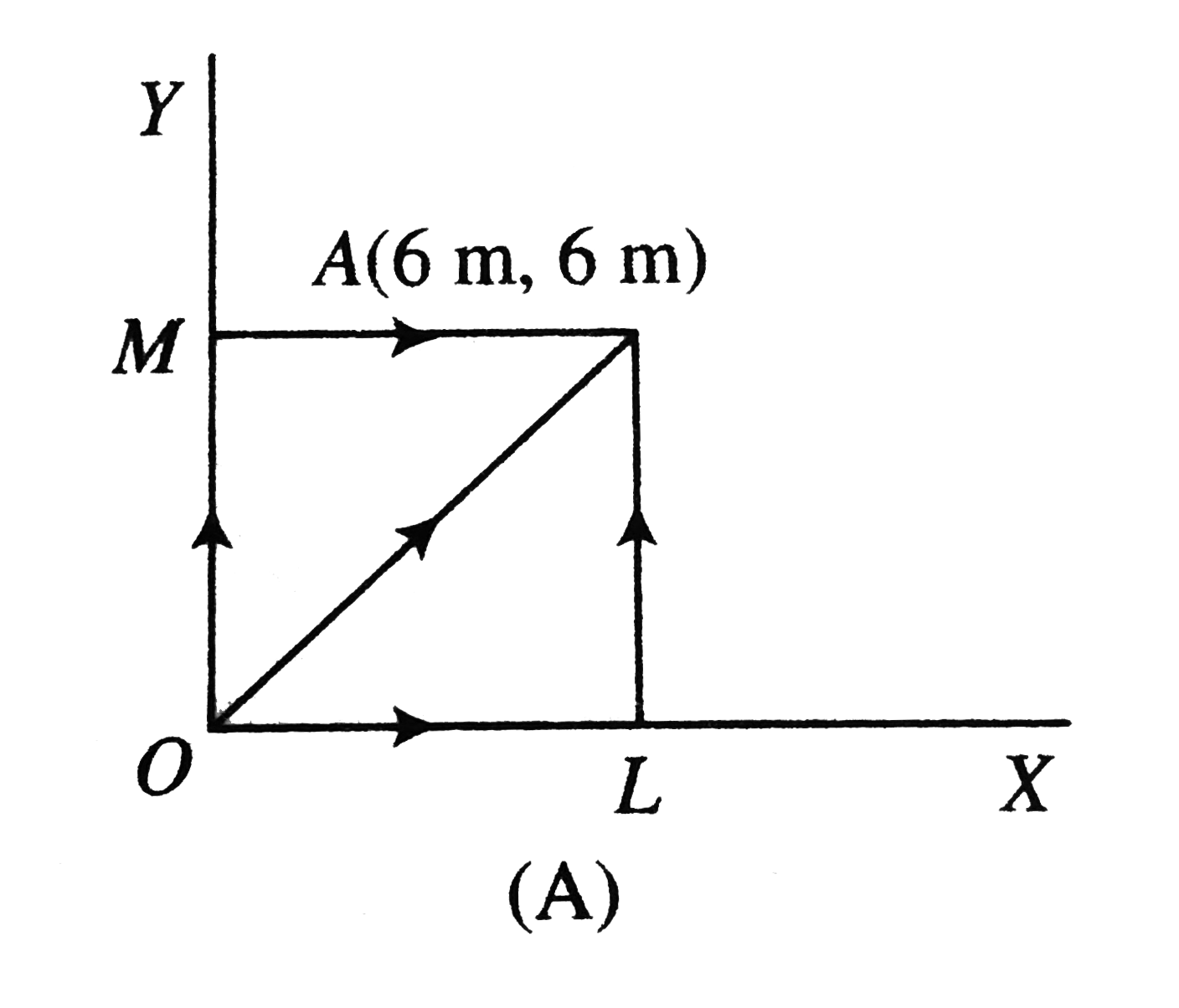
Force acting on a particle moving in the x-y plane is →F=(y2ˆi+xˆj)N, x and y are in metre. As shown in figure, the particle moves from the origin O to point A (6m,6m). The figure shows three paths, OLA, OMA, and OA for the motion of the particle from O to A.
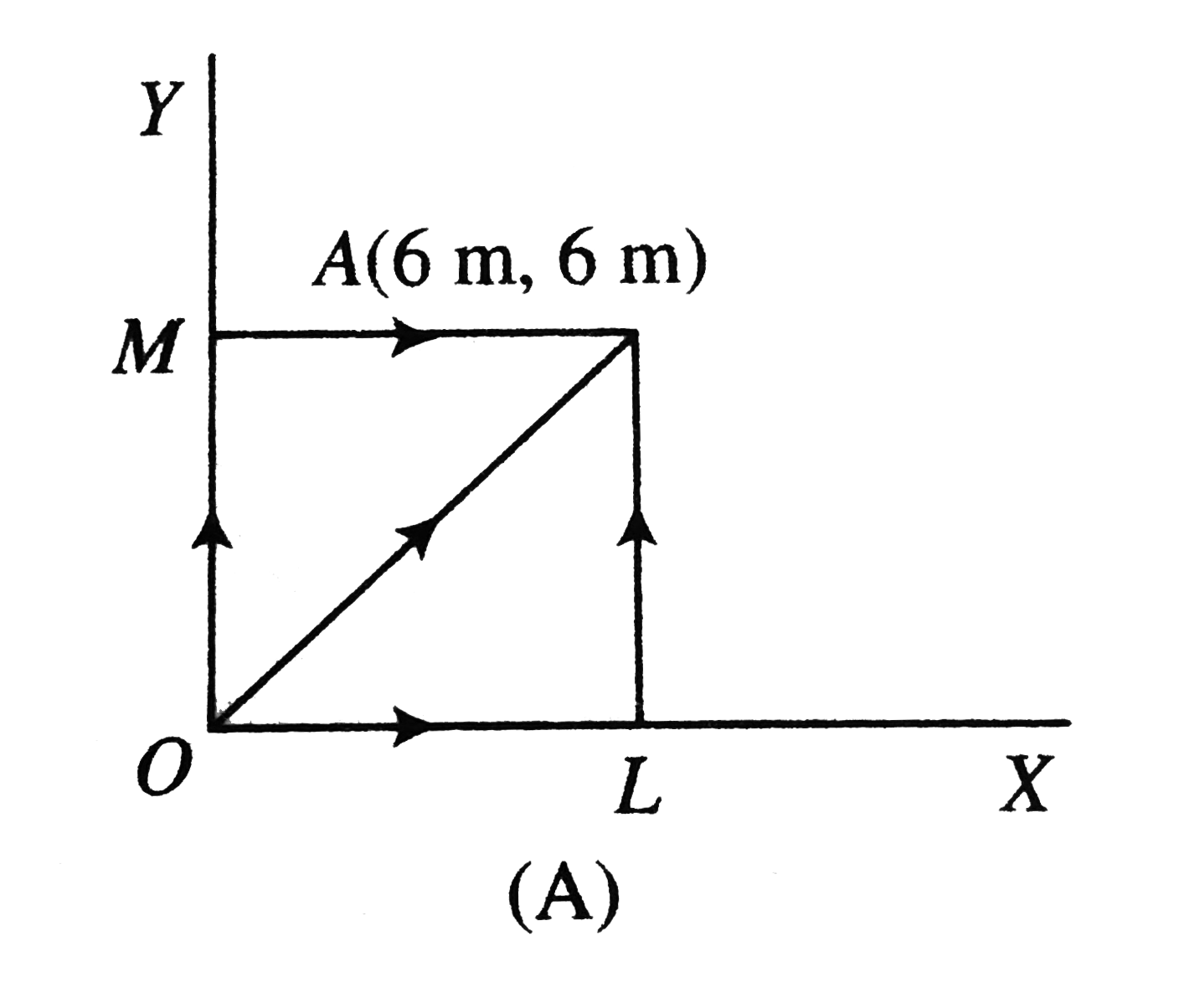
Which of the following is correct? View SolutionQuestion 300
Force acting on a particle moving in the x-y plane is →F=(y2ˆi+xˆj)N, x and y are in metre. As shown in figure, the particle moves from the origin O to point A (6m,6m). The figure shows three paths, OLA, OMA, and OA for the motion of the particle from O to A.

Which of the following is correct? View SolutionQuestion 301
Force acting on a particle moving in the x-y plane is →F=(y2ˆi+xˆj)N, x and y are in metre. As shown in figure, the particle moves from the origin O to point A (6m,6m). The figure shows three paths, OLA, OMA, and OA for the motion of the particle from O to A.
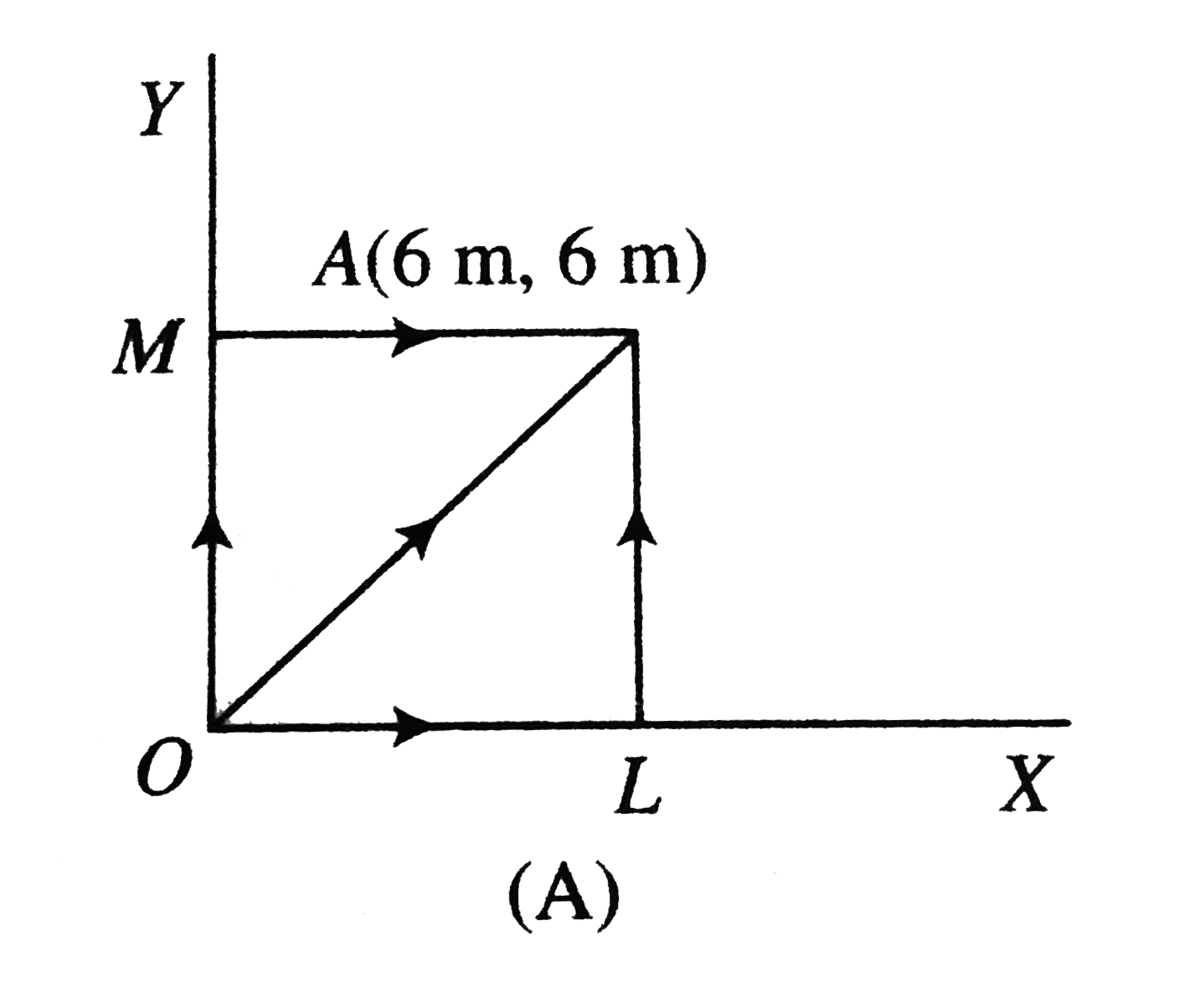
Work done for motion along path OA is nearly
 View Solution
View SolutionQuestion 302
Force acting on a particle moving in the x-y plane is →F=(y2ˆi+xˆj)N, x and y are in metre. As shown in figure, the particle moves from the origin O to point A (6m,6m). The figure shows three paths, OLA, OMA, and OA for the motion of the particle from O to A.

Which of the following is correct? View SolutionQuestion 303
Force acting on a particle moving in the x-y plane is →F=(y2ˆi+xˆj)N, x and y are in metre. As shown in figure, the particle moves from the origin O to point A (6m,6m). The figure shows three paths, OLA, OMA, and OA for the motion of the particle from O to A.
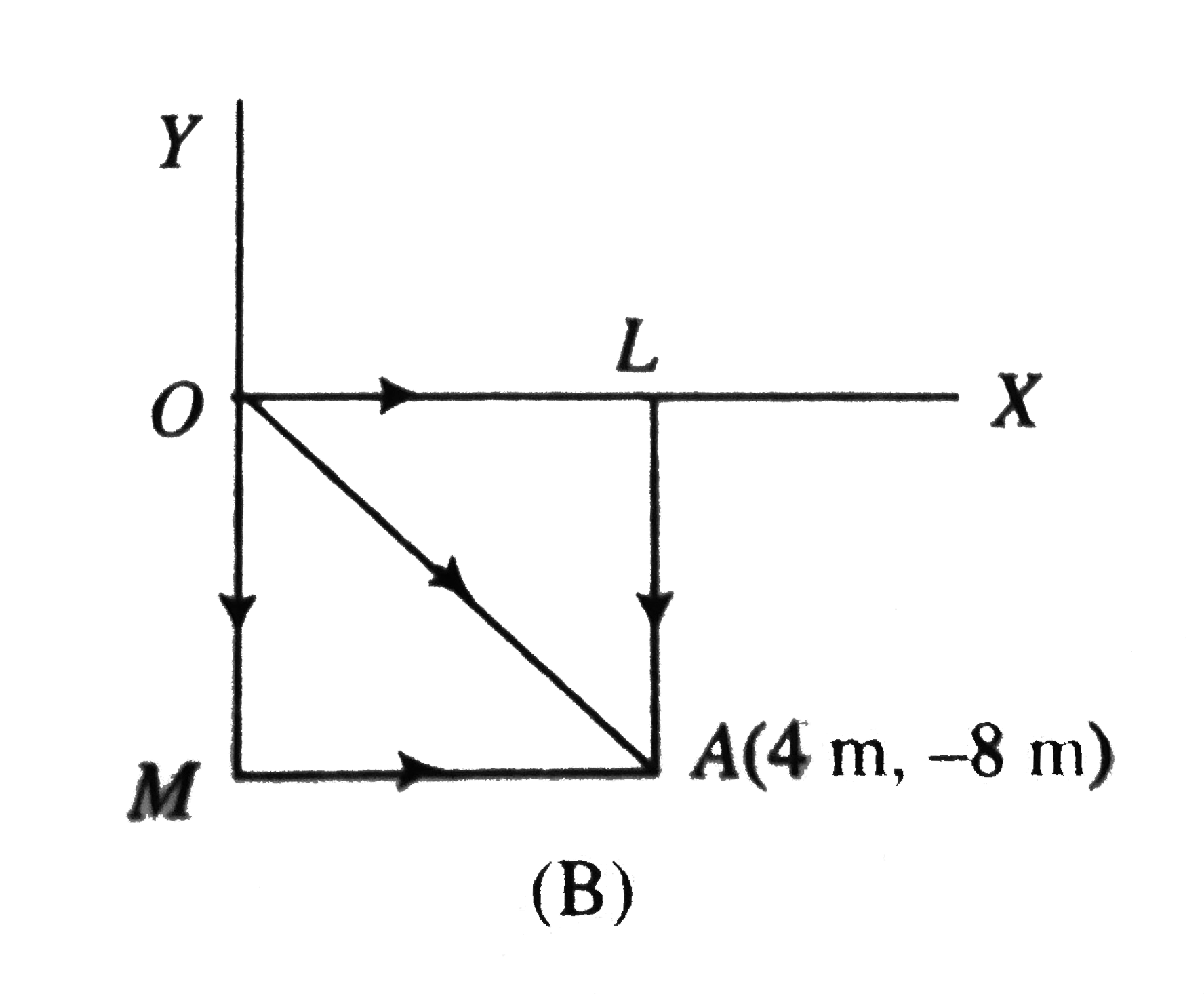
Now consider another situation. A force →F=(4ˆi+3ˆj)N acts on a particle of mass 2kg. The particle under the action of this force moves from the origin to a point A (4m,−8m). Initial speed of the particle, i.e., its speed at the origin is 2√6ms−1. Figure shows three paths for the motion of the particle from O to A.
Speed of the particle at A will be nearlyView SolutionQuestion 304
Force acting on a particle moving in the x-y plane is →F=(y2ˆi+xˆj)N, x and y are in metre. As shown in figure, the particle moves from the origin O to point A (6m,6m). The figure shows three paths, OLA, OMA, and OA for the motion of the particle from O to A.
Now consider another situation. A force →F=(4ˆi+3ˆj)N acts on a particle of mass 2kg. The particle under the action of this force moves from the origin to a point A (4m,−8m). Initial speed of the particle, i.e., its speed at the origin is 2√6ms−1. Figure shows three paths for the motion of the particle from O to A.
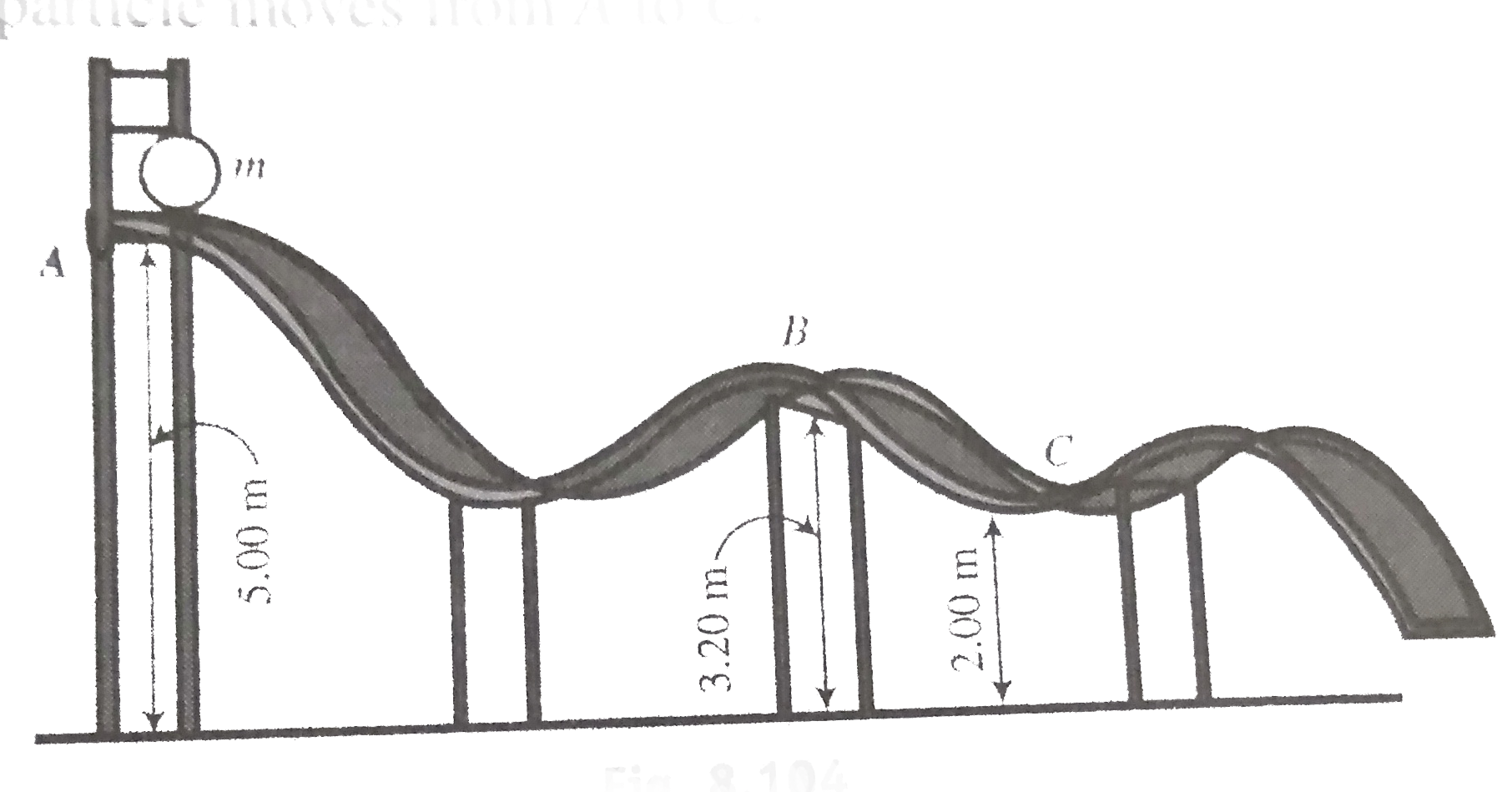
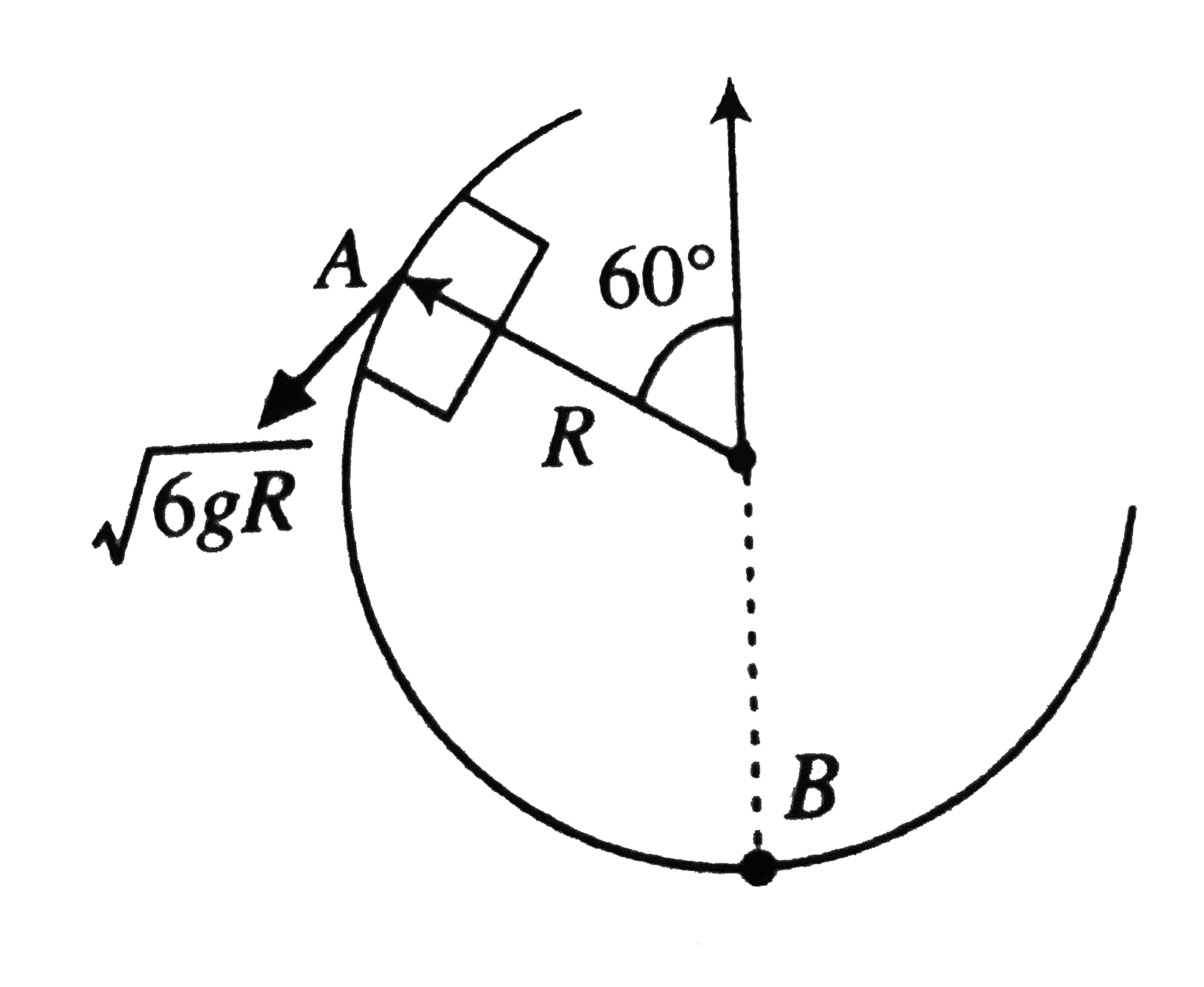
If the potential energy at O is 16J, the potential energy at A will beView SolutionQuestion 305
A small block of mass m is pushed on a smooth track from position A with a velocity 2√5 times the minimum velocity required to reach point D. The block will leave the contact with track at the point where normal force between them becomes zero.
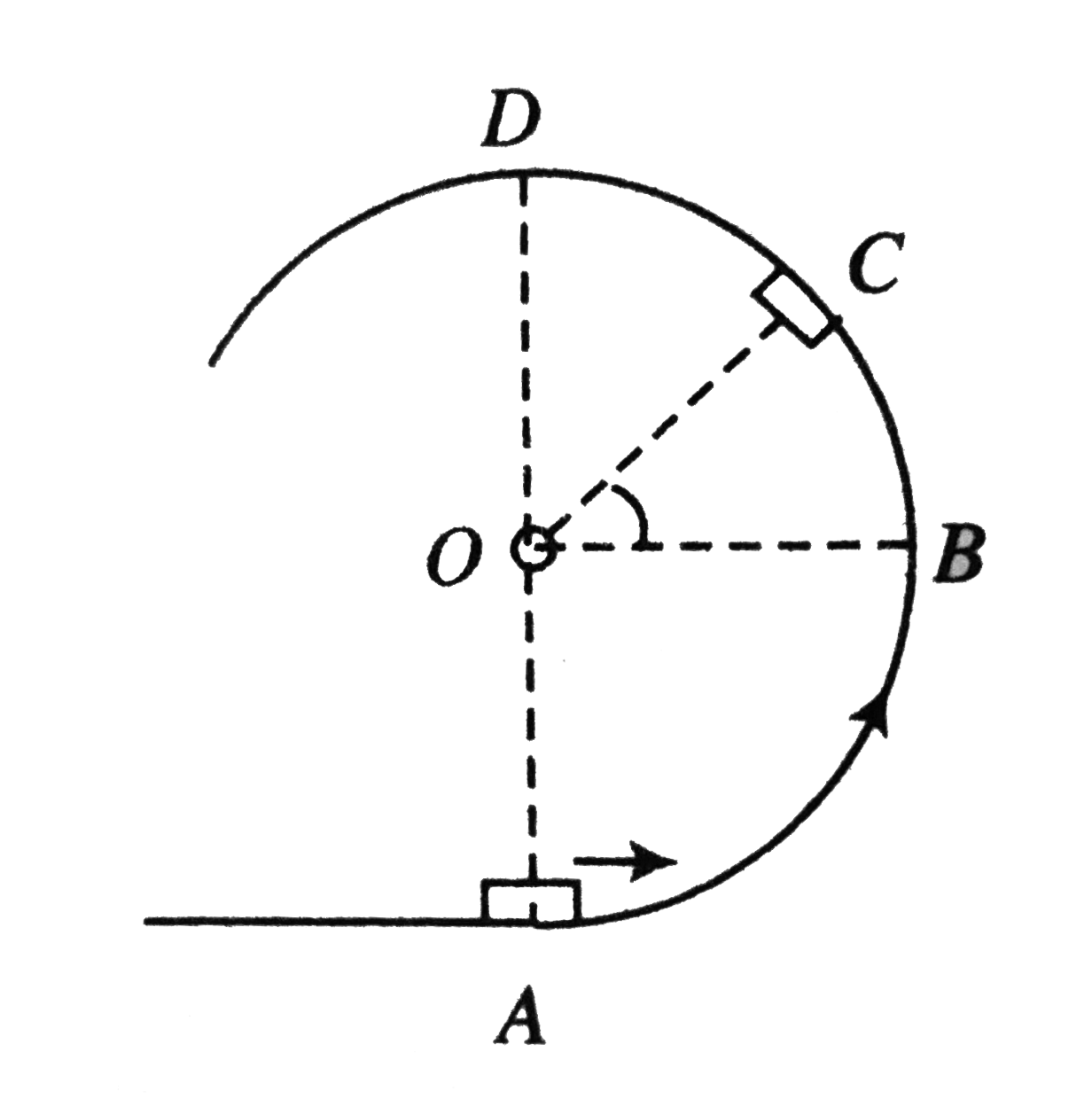
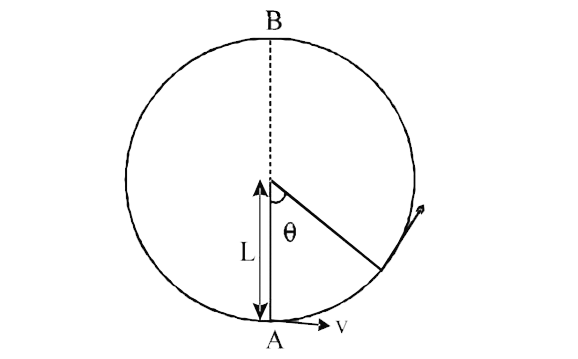
At what angle θ with horizontal does the block gets separated from the track?View SolutionQuestion 306
A small block of mass m is pushed on a smooth track from position A with a velocity 2√5 times the minimum velocity required to reach point D. The block will leave the contact with track at the point where normal force between them becomes zero.

At what angle θ with horizontal does the block gets separated from the track?View SolutionQuestion 307
A small block of mass m is pushed on a smooth track from position A with a velocity 2√5 times the minimum velocity required to reach point D. The block will leave the contact with track at the point where normal force between them becomes zero.
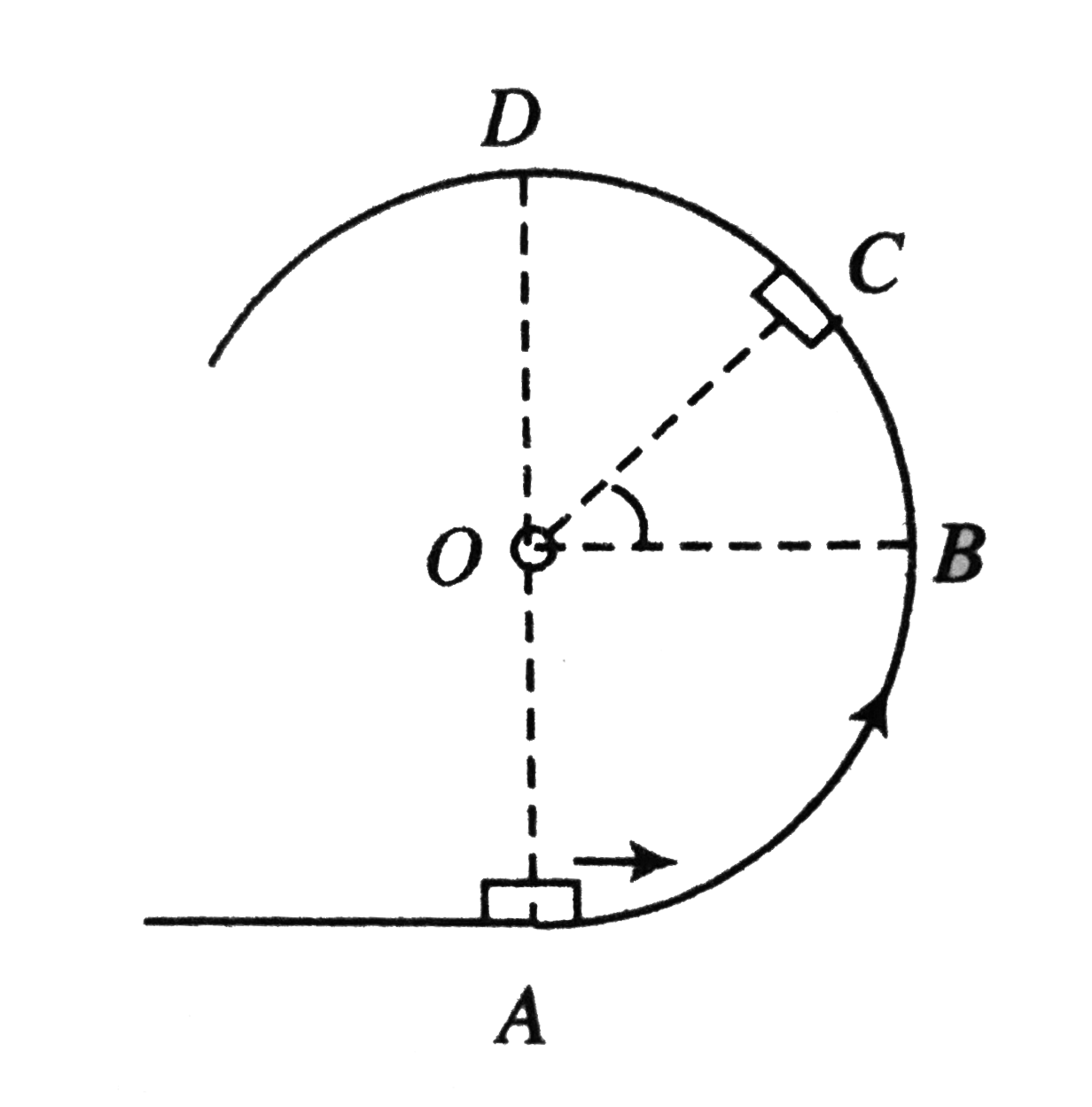
Find where the maximum contact force occurs between the block and the track.View SolutionQuestion 308
A force F=50N is applied at one end of a string, the other end of which is tied to a block of mass 10kg. The block is free to move on a frictionless horizontal surface. Take initial instant as θ=30∘ and final instant as θ=37∘. For the time between these two instants, answer teh following questions?
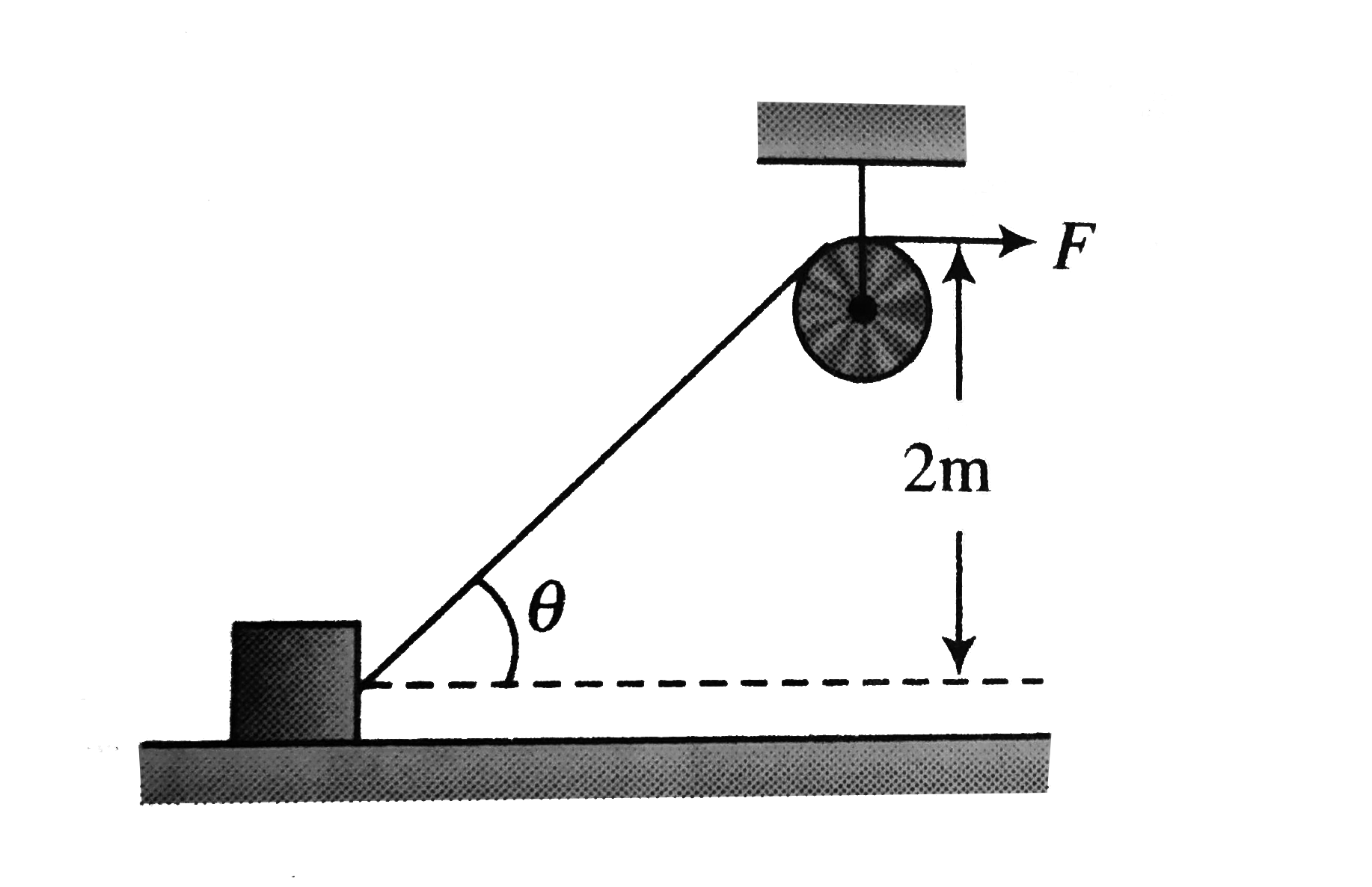
Net work done by the force F on the block is View SolutionQuestion 309
A force F=50N is applied at one end of a string, the other end of which is tied to a block of mass 10kg. The block is free to move on a frictionless horizontal surface. Take initial instant as θ=30∘ and final instant as θ=37∘. For the time between these two instants, answer teh following questions?
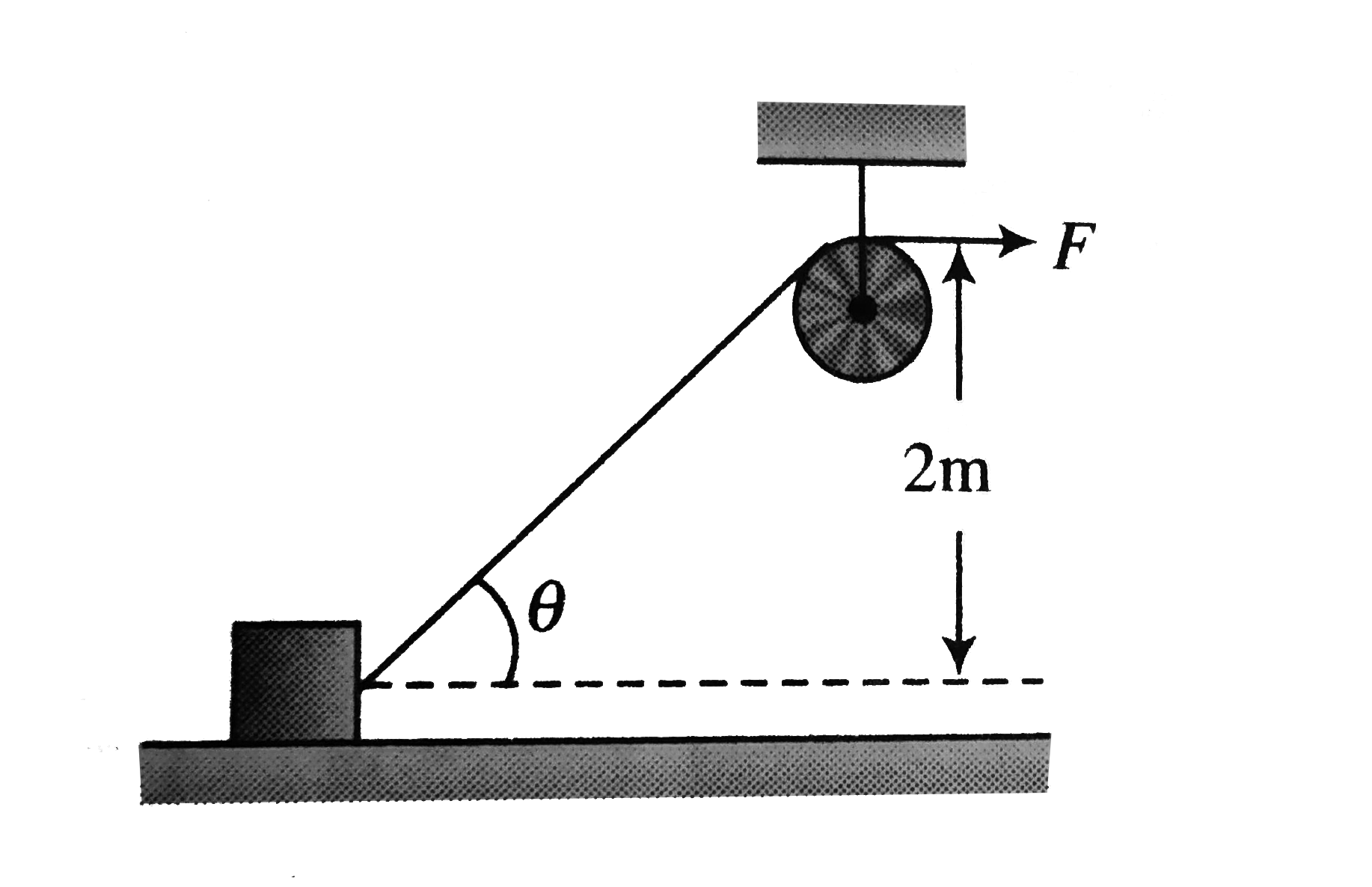
What is the final velocity of the block if initially it was at rest?View SolutionQuestion 310
A force F=50N is applied at one end of a string, the other end of which is tied to a block of mass 10kg. The block is free to move on a frictionless horizontal surface. Take initial instant as θ=30∘ and final instant as θ=37∘. For the time between these two instants, answer teh following questions?
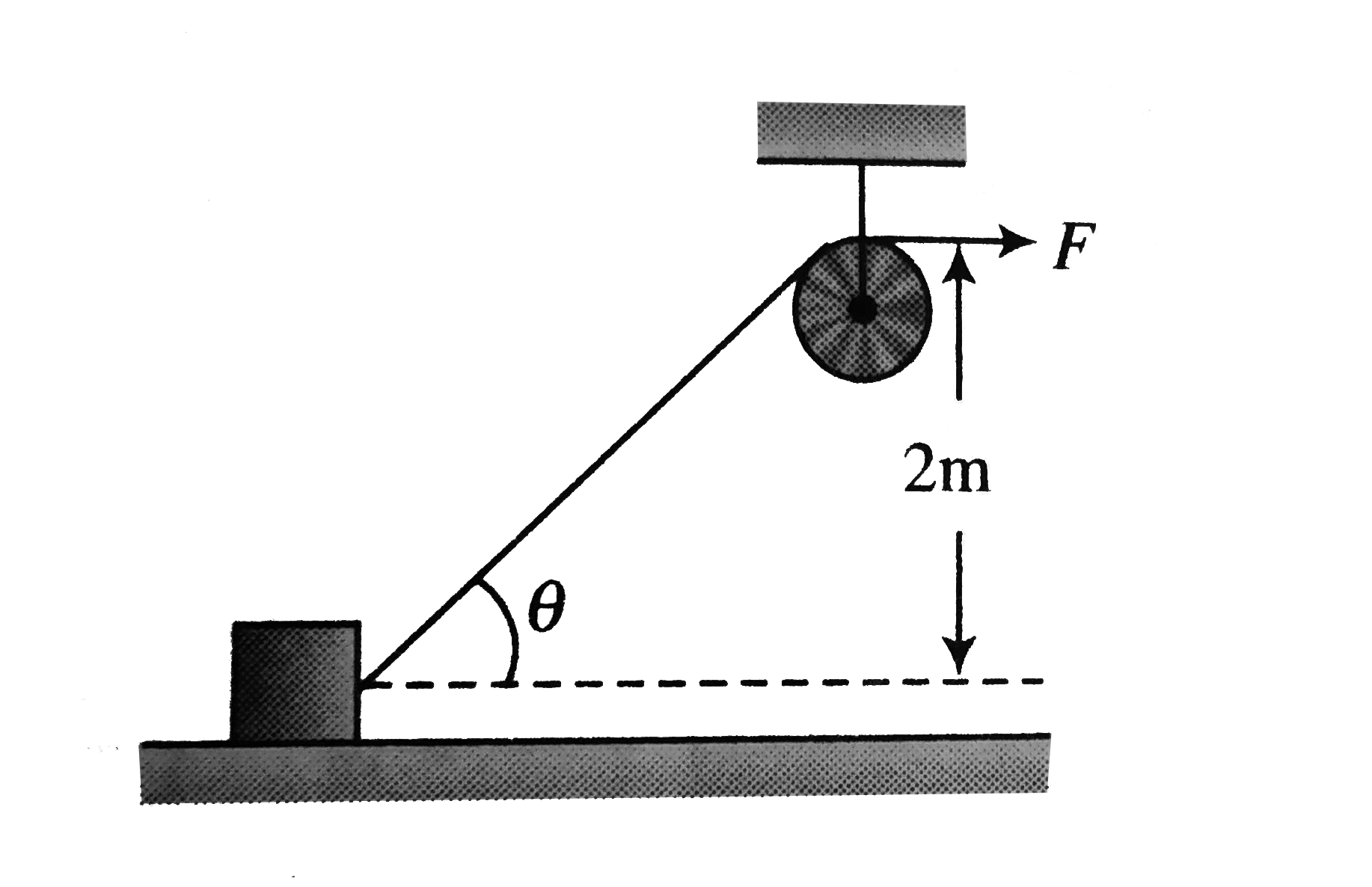
Find the ratio of initial acceleration to final acceleration of the blockView SolutionQuestion 312
An insect jumps from ball A onto ball B, which are suspended from inextensible light strings each of length L=8cm. The mass of each ball and insect is same. What should be the minimum relative velocity (in ms−1) of jump of insect w.r.t. ball A, if both the balls manage to complete the full circle?
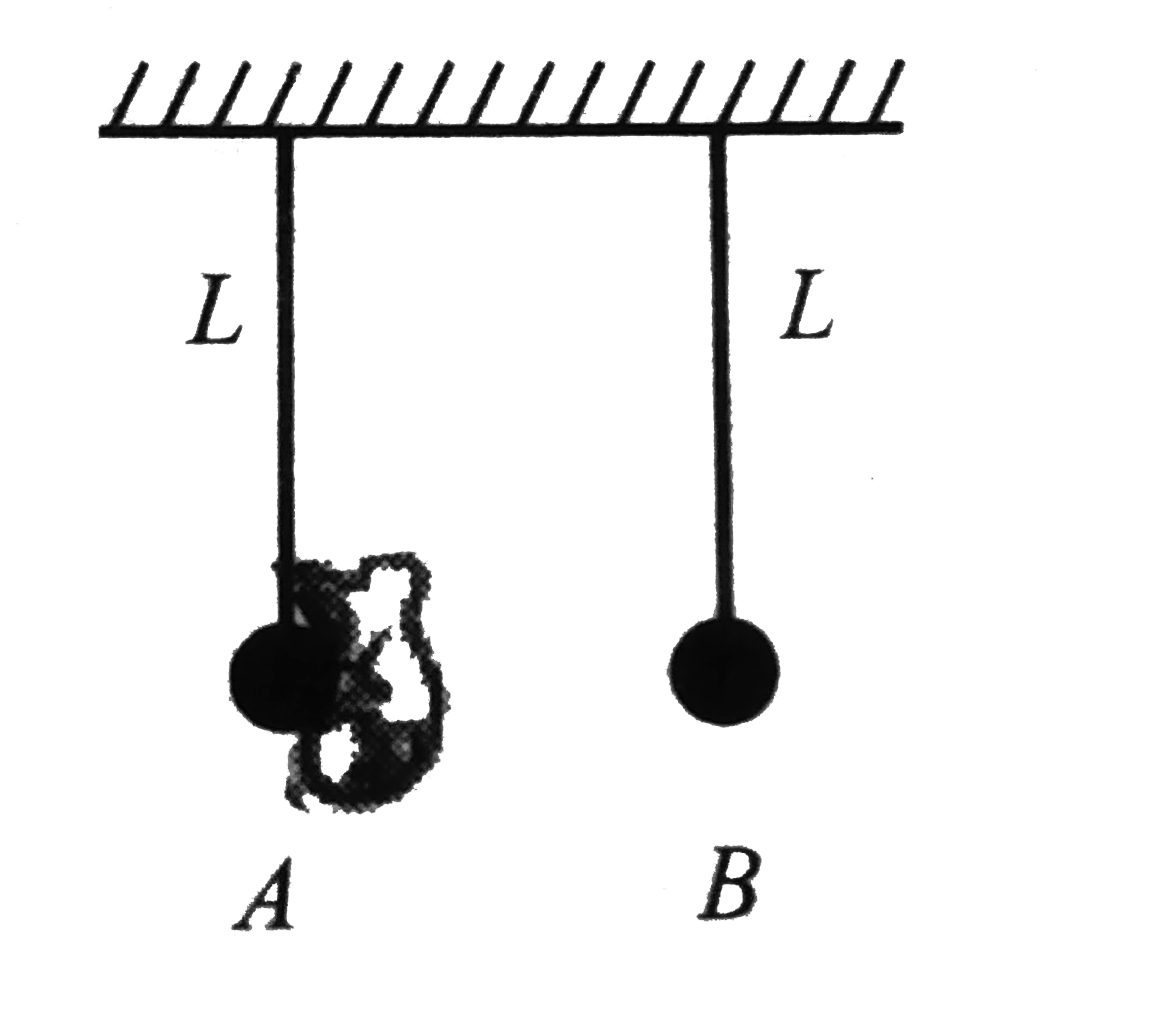 View Solution
View SolutionQuestion 316
In figuer, shown all the surfaces are frictionless, and mass of the block is m=100g. The block and the wedge are held initially at rest. Now the wedge is given a horizontal acceleration of 10ms−2 by applying a force on the wedge, so that the block does not slip on the wedge. Then find the work done in joules by the normal force in ground frame on the block in 1s.
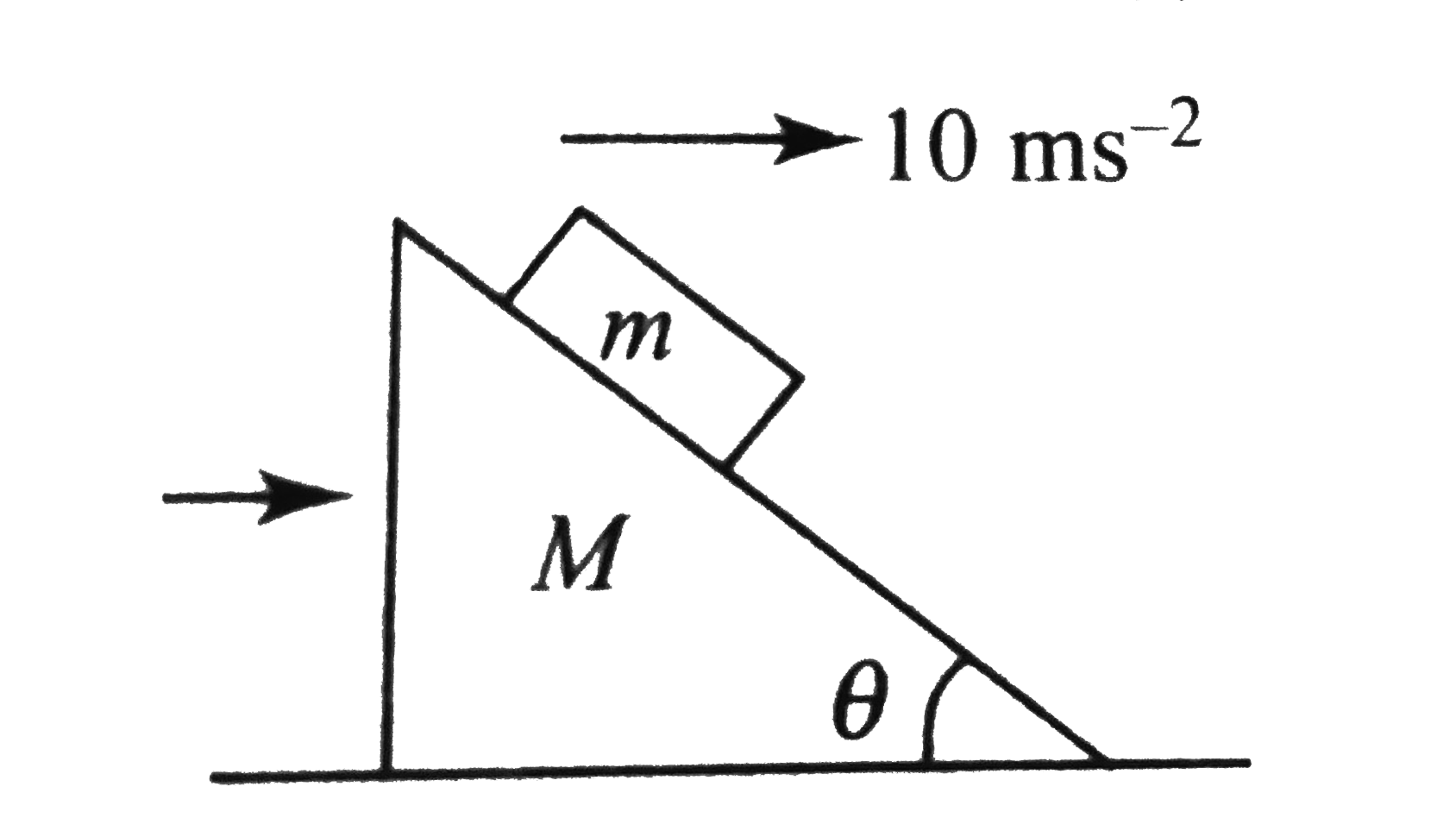 View Solution
View SolutionQuestion 319
The arrangement shown in figure is at rest. An ideal spring of natural length l0 having spring constant k=220Nm−1, is connected to block A. Blocks A and B are connected by an ideal string passing through a friction less pulley. The mass of each block A and B is equal to m=2kg when the spring was in natural length, the whole system is given an acceleration →a as shown. If coefficient of friction of both surfaces is μ=0.25, then find the maximum extension in 10(m) of the spring. (g=10ms−2).
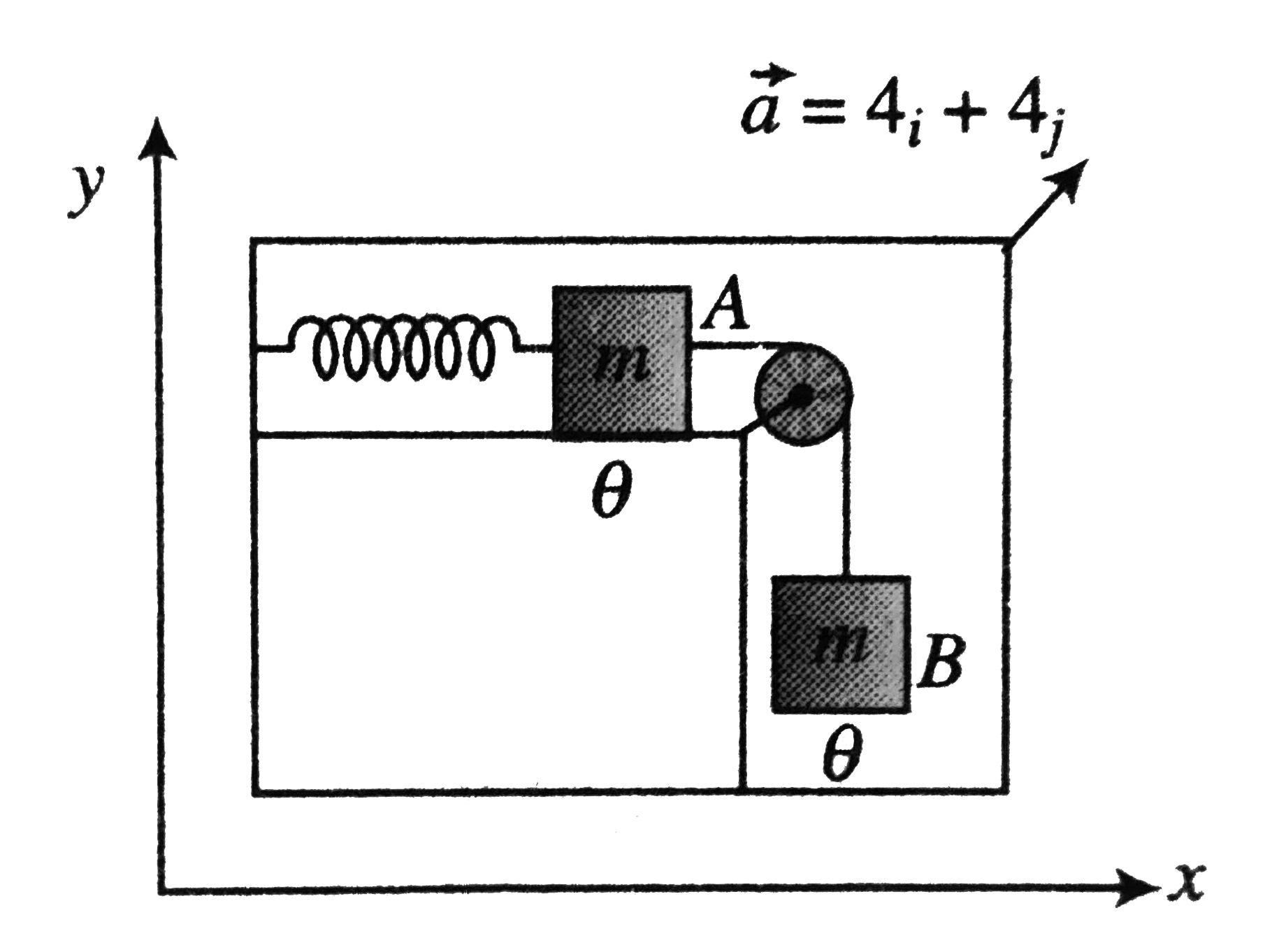 View Solution
View SolutionQuestion 321
One end of a spring of force constant k1 is attached to the ceiling of an elevator. A block of mass 1.5kg is attached to the other end. Another spring of force constant k2 is attached to the bottom of the mass and to the floor of the elevator as shown in figure. At equilibrium, the deformation in both the spring is equal and is 40cm. If the elevator moves with constant acceleration upward, the additional deformation in both the spring is 8cm. Find the elevator's accelerationn ( g=10ms−2).
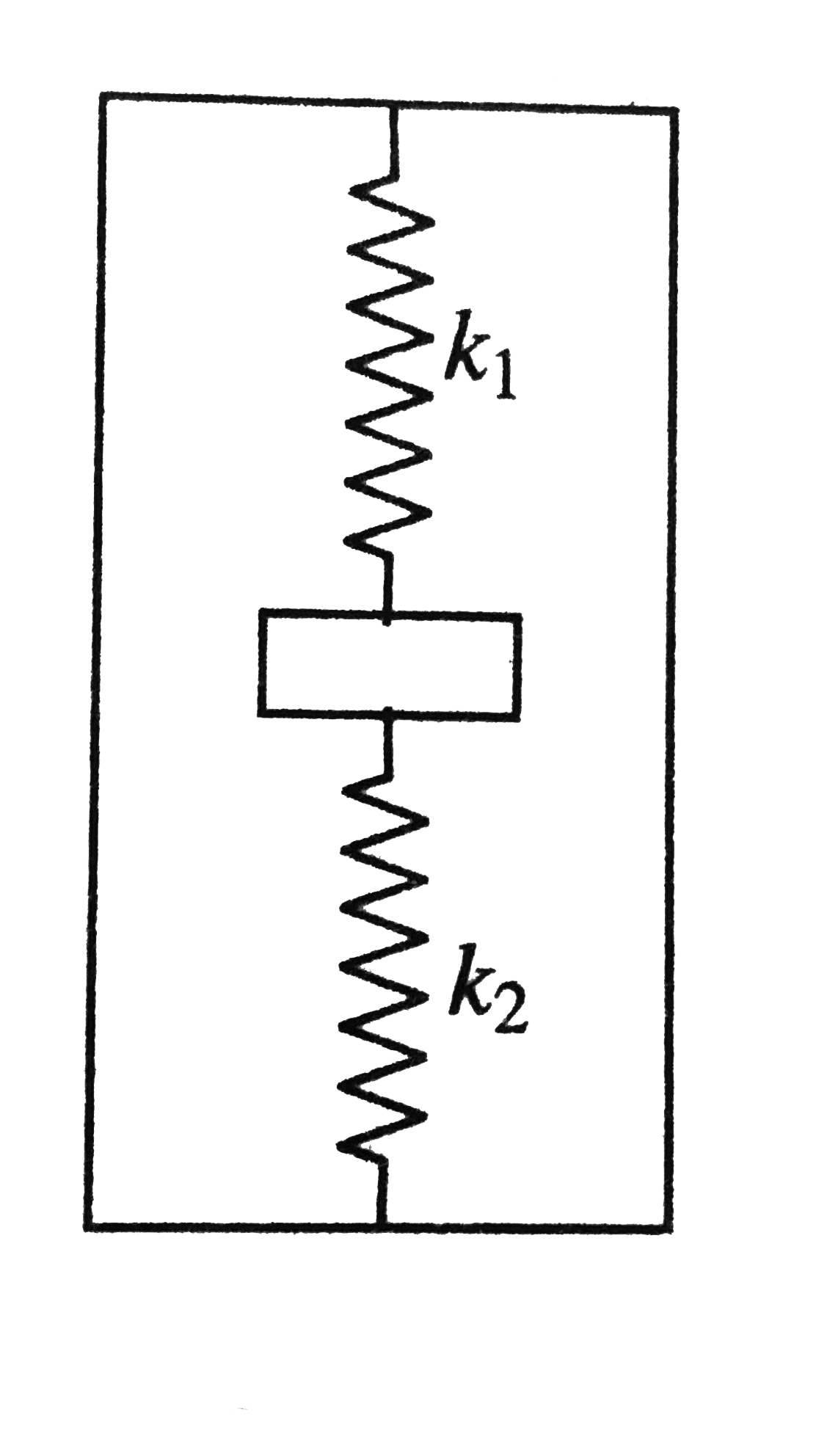 View Solution
View SolutionQuestion 322
A system consists of two identical cubes, each of mass 3kg, linked together by a compressed weightless spring of force constant 1000Nm−1. The cubes are also connected by a thread which is burnt at a certain moment. At what minimum value of initial compression x0 (in cm) of the spring will the lower cube bounce up after the thread is burnt together?
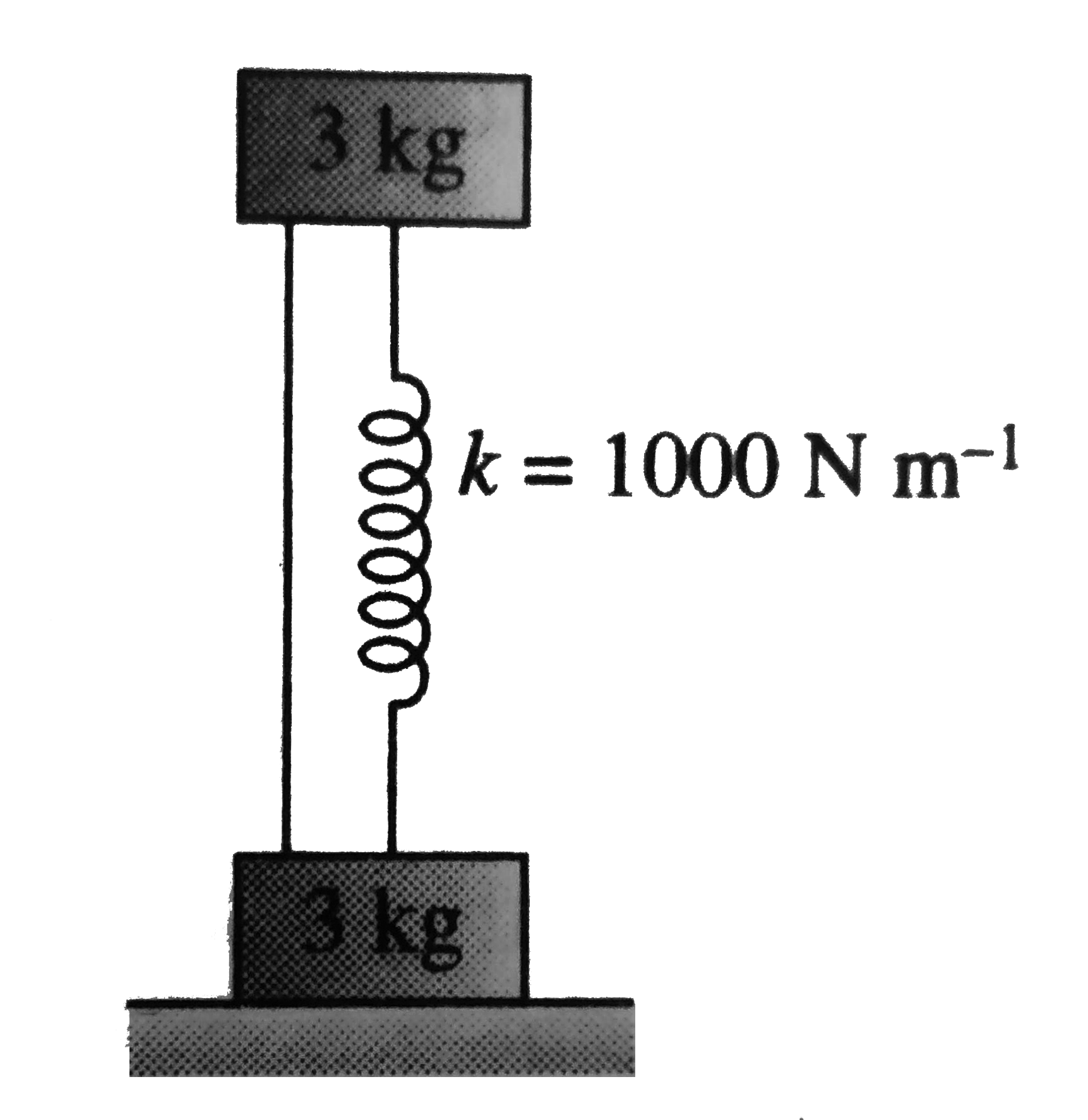 View Solution
View SolutionQuestion 323
A particle of mass 5kg is free to slide on a smooth ring of radius r=20cm fixed in a vertical plane. The particle is attached to one end of a spring whose other end is fixed to the top point O of the ring. Initially, the particle is at rest at a point A of the ring such that ∠OCA=60∘, C being the centre of the ring. The natural length of the spring is also equal to r=20cm. After the particle is released and slides down the ring, the contact force between the particle and the ring becomes zero when it reaches the lowest position B. Determine the force constant (in×102Nm−1) of the spring.
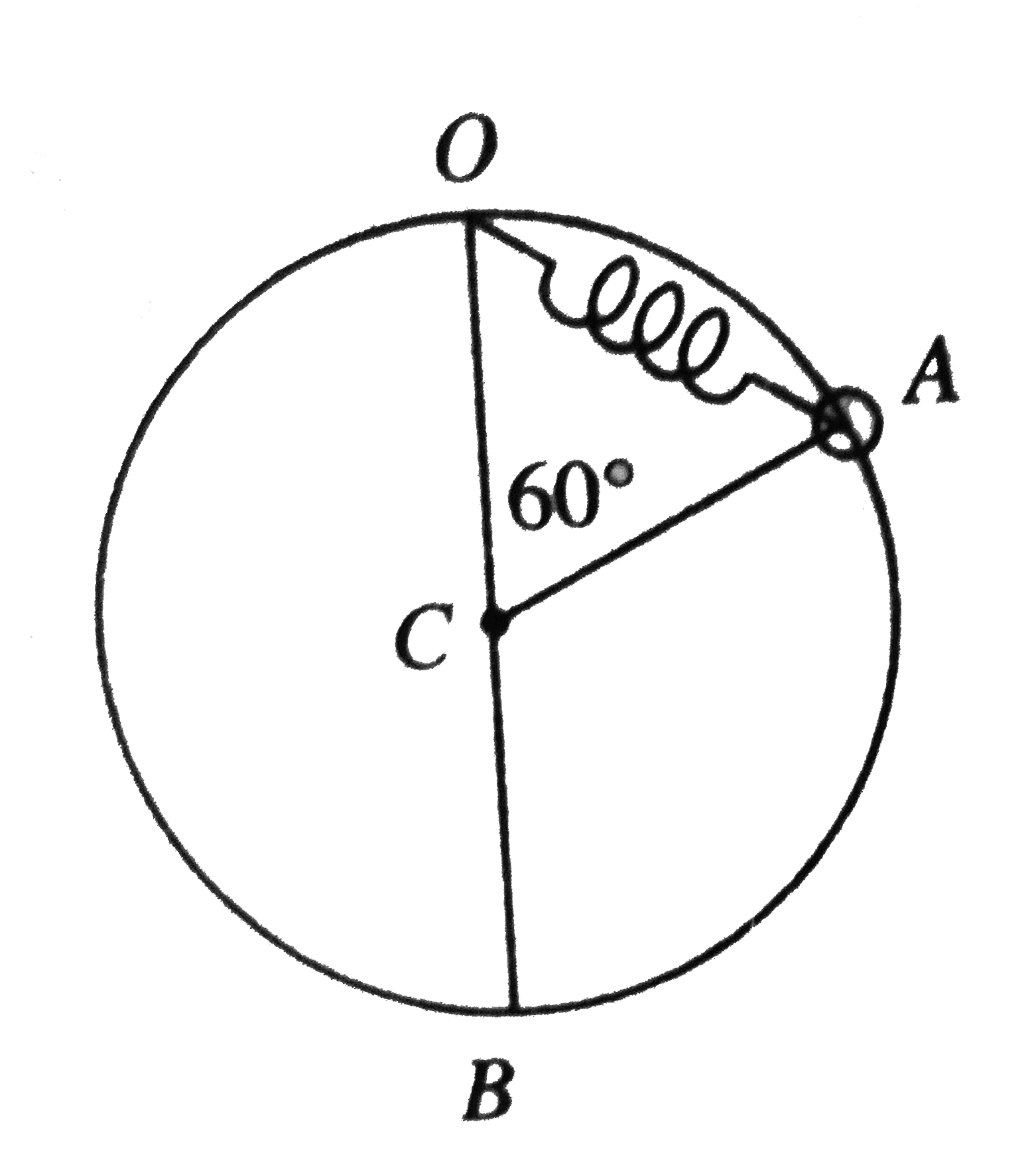 View Solution
View SolutionQuestion 324
A 2144kg freight car roles along rails with negligible friction. The car is brought to rest by a combination of two coiled springs as illustrated in figure. Both springs are described by Hooke's law with k1=1600Nm−1 and k2=3400Nm−1. After the first spring compresses a distance of 30.0cm, the second spring acts with the first to increase the force as additional compression occurs as shown in the graph in figure. The car comes to rest 50.0cm after first contracting the two-spring system. Find the car's initial speed (in×10−1Nm−1).
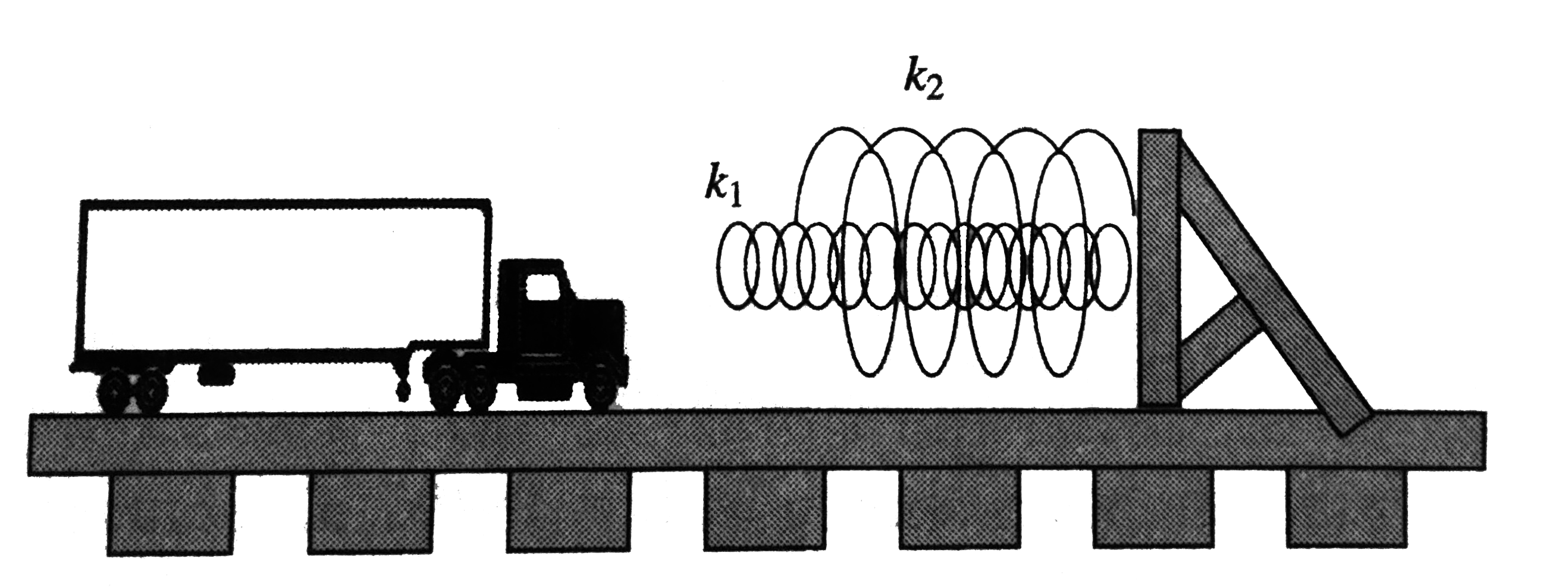
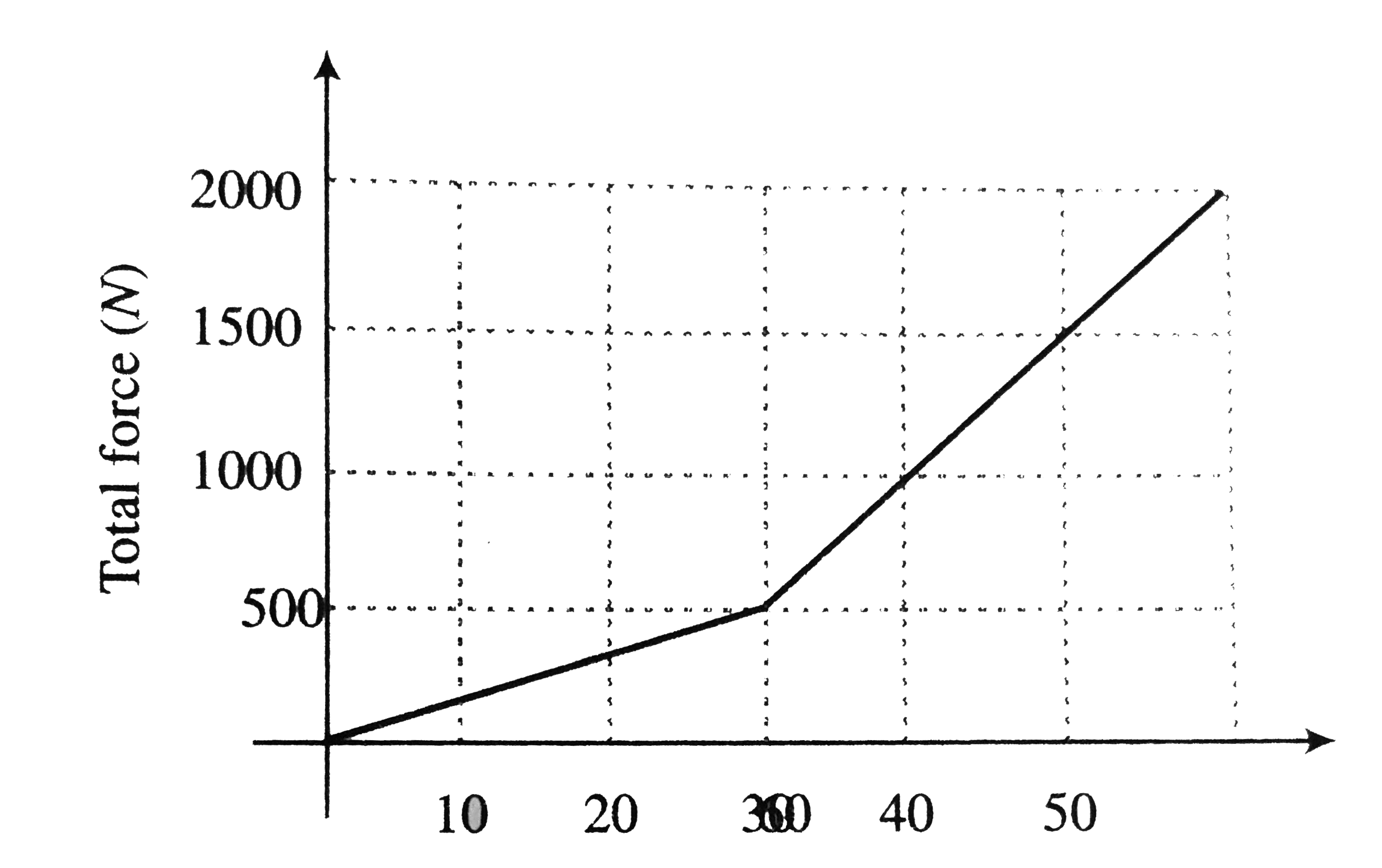 View Solution
View SolutionQuestion 329
A stone is tied to a string of length l and is whirled in a vertical circle with the other end of the string as the centre. At a certain instant of time, the stone is at its lowest position and has a speed u. The magnitude of the change in velocity as it reaches a position where the string is horizontal (g being acceleration due to gravity) is View SolutionQuestion 330
A force F=−kˆi+xˆj where k is a positive constant, acts on a praricle moving in the xy plane. Starting from the origin, the particle is taken along the positive x - axis to the point (a,0) and then parallel to the y-axis to the point (a,a) the total work done by the formce on the particle isView SolutionQuestion 334
A particle, which is constrained to move along x-axis, is subjected to a force in the some direction which varies with the distance x of the particle from the origin an F(x)=−kx+ax3. Here, k and a are positive constants. For x(≥0, the functional form of the potential energy (u) U of the U (x) the particle is.
(a)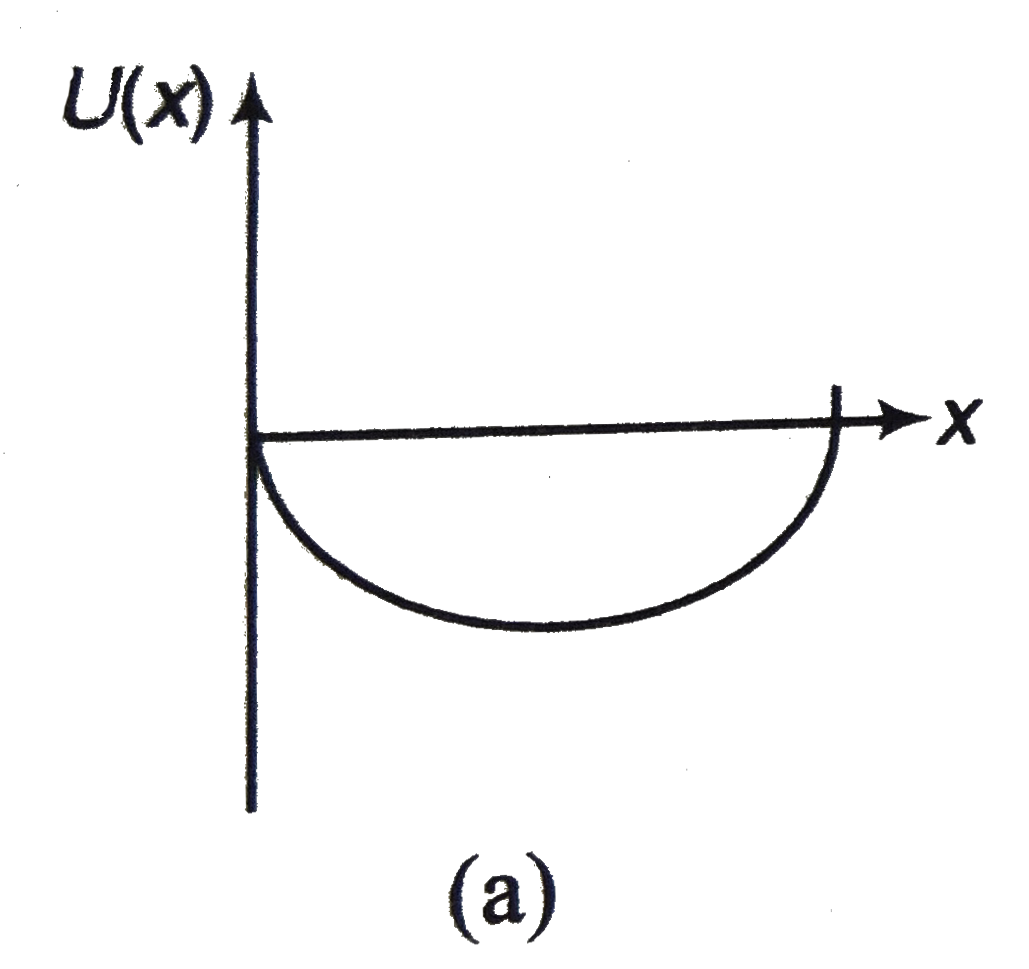 , (b)
, (b) 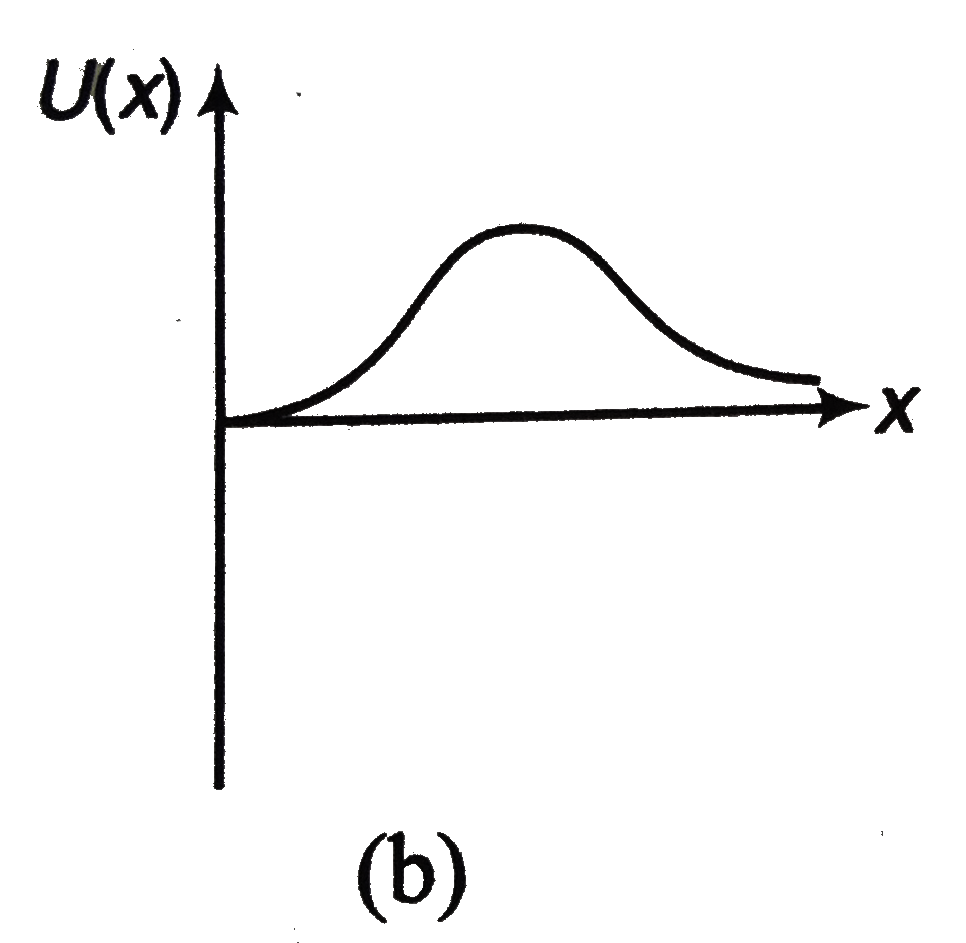 , (c)
, (c) 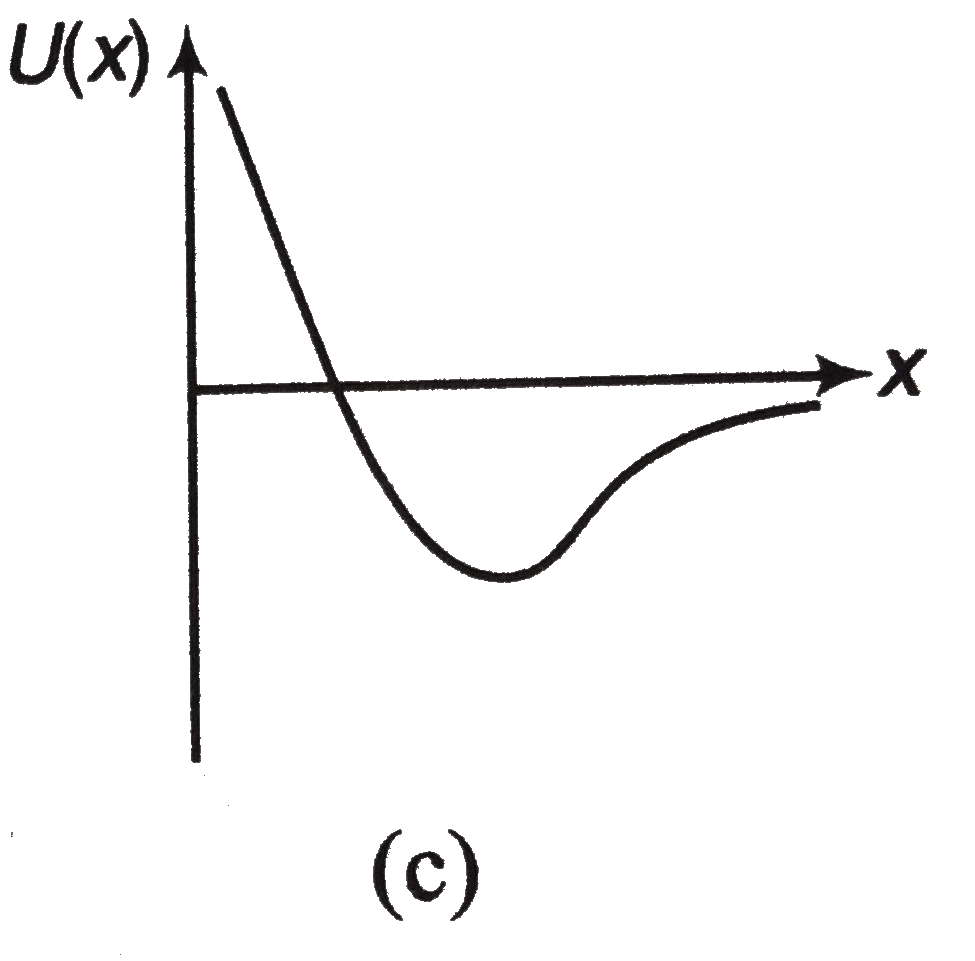 , (d)
, (d) 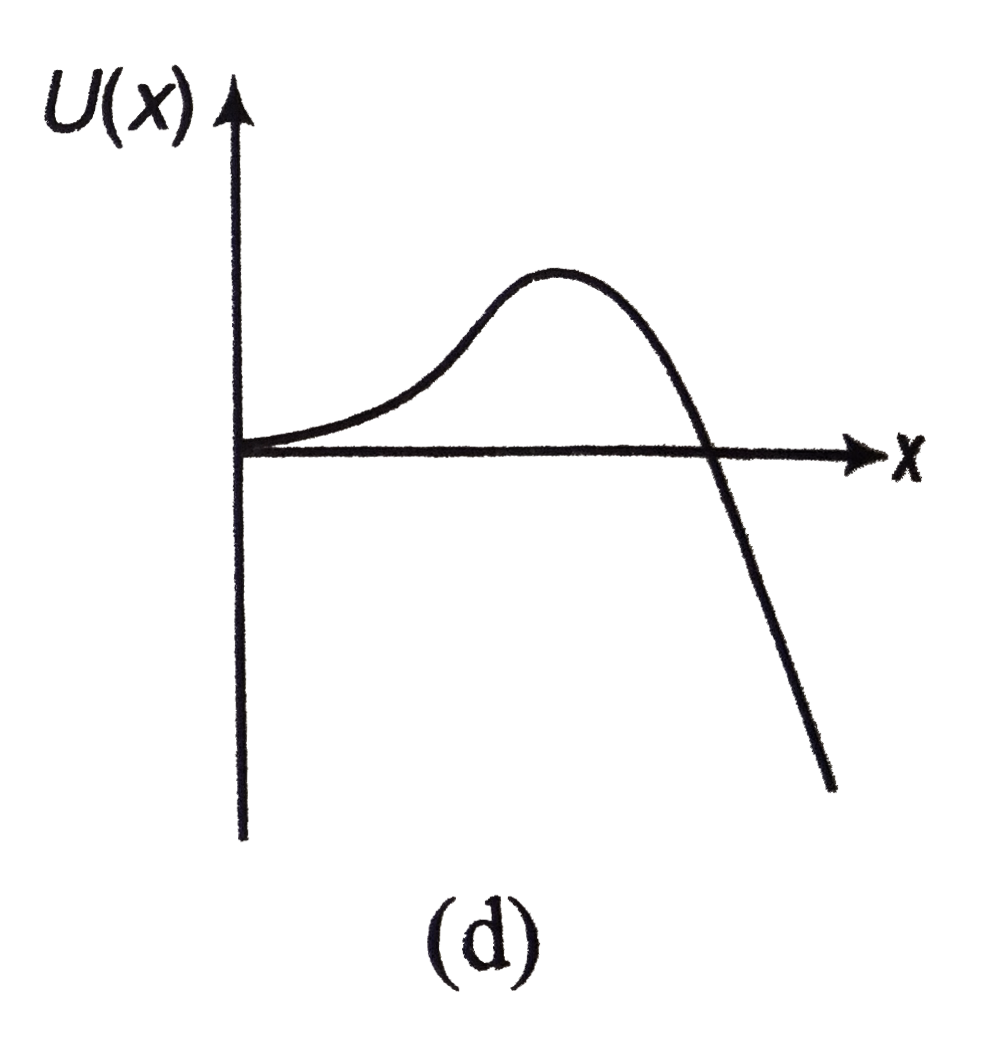 . View Solution
. View SolutionQuestion 339
A block (B) is attached to two unstriched sprig S1 and S2 with spring constant K and 4K , respectively (see fig 1) The other ends are atteched in identical support M1 and M2 not attached in the walls . The springs and supports have negligible mass . There is no friction anywhere . The block B is displaced toword wall 1 by a small distance x (figure (ii)) and released . The block return and moves a maximum distance y towards wall 2.Displacements x and y are measured w.r.to the equalibrum of the block B and the ratio y/x is
 View Solution
View SolutionQuestion 342
A tennis ball dropped on a horizontal smooth surface , it because back to its original position after hitting the surface the force on the bell during the collision is proportional to the length of compression of the bell . Which one of the following skethes desches discribe the variation of its kinetic energy K with time 1 mass apporiandly ? The figure as only illistrative and not to the scale . View SolutionQuestion 343
A wire, which passes through the hole in a small bead, is bent in the form of quarter of a circle. The wire is fixed vertically on ground as shown in the figure. The bead is released from near the top of the wire and it slides along the wire without friction. As the bead moves from A to B, the force it applies on the wire is
 View Solution
View SolutionQuestion 344
A simple pendulum of length L and mass (bob) M is oscillating in a plane about a vertical line between angular limit −ϕ and +ϕ. For an angular displacement θ(|θ|<ϕ), the tension in the string and the velocity of the bob are T and V respectively. The following relations hold good under the above conditions:View SolutionQuestion 346
Two identical blocks A and B, each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k with the spring at its natural length. A third identical block C (mass m) movimng with a speed v along the line joining A and B collides with A, the maximum compression in the spring isView SolutionQuestion 347
Asseration : A block of mass m starts moving on a rough horizontal surface with a velocity v. It stops due to friction between the block and the surface after moving through a ceratin distance. The surface is now tilted to an angle of 30∘ with the horizontal and same block is made to go up on the surface with the same initial velocity v. The decrease in the mechanical energy in the second situation is small than the first situation.
Reason : The coefficient of friction between the block and the surface decreases with the increase in the angle of inclination.View SolutionQuestion 348
A small block of mass 1 kg is a circular are of ratius 40 m . The block sides along the track without topping and a frictionnal force acts on it in the direction opposite in the instrmens velocity . The work done in evercoming the friction up to the point Q as shown is the figure below is 150J
(Take the acceleration due to gravity g=10ms−2)
The speed of the block when it reaches the point Q is View SolutionQuestion 349
A small block of mass 1 kg is a circular are of ratius 40 m . The block sides along the track without topping and a frictionnal force acts on it in the direction opposite in the instrmens velocity . The work done in evercoming the friction up to the point Q as shown is the figure below is 150J
(Take the acceleration due to gravity g=10ms−2)
The magnitude of the normal reaction that acts on the block at the point Q is View SolutionQuestion 350
A light inextensible string that gas over a smoth fixed polley as shown in the figure connect two blocks of mases it 0.36 kg and 0.72 kg Taking g=10ms−2 , find the work done by the string on the block of mass 0.36 kg doring the first second after the system is released from rest ,
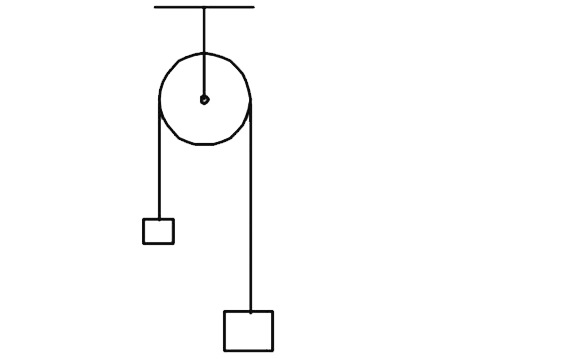 View Solution
View SolutionQuestion 351
A block of mass 0.18kg is attached to a spring of force-constant 2N/m. The coefficient of friction between the block and the floor is 0.1 Initially the block is at rest and the spring is un-stretched. An impulse is given to the block as shown in the figure. The block slides a distance of 0.06m and comes to rest for the first time. The initial velocity of the block in m//s is V=N/10. Then N is :
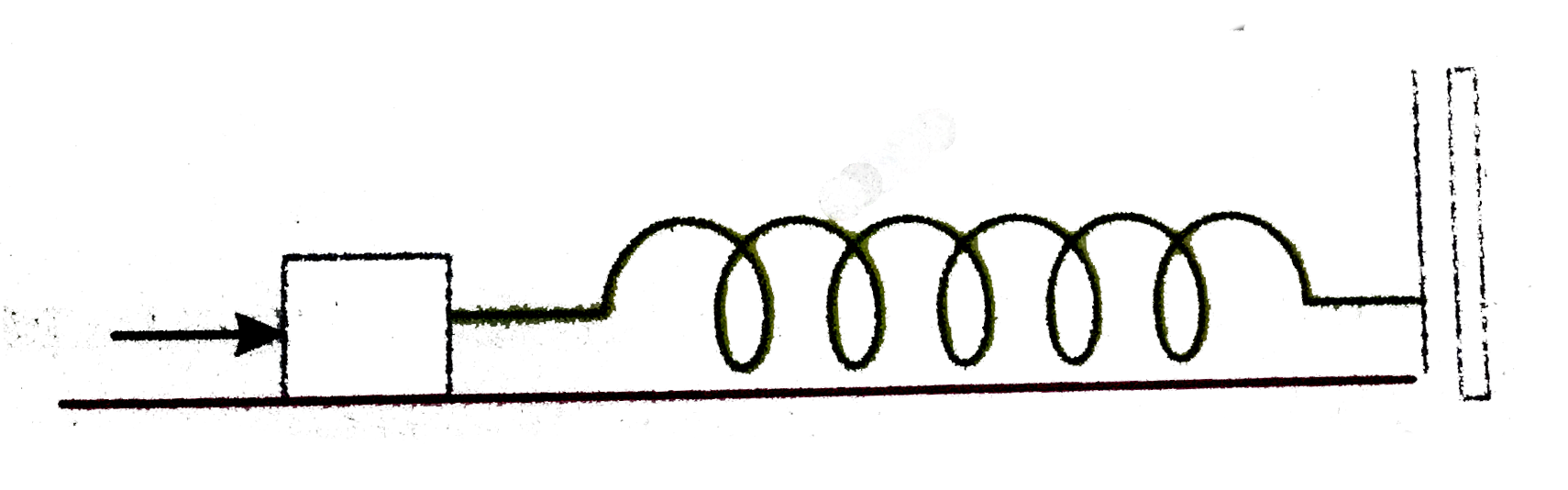 .View Solution
.View SolutionQuestion 352
A bob of mass m, suspended by a string of length l1 is given a minimum velocity required to complete a full circle in the vertical plane. At the highest point, it collides elastically with another bob of mass m suspended by a string of length l2, which is initially at rest. Both the strings are mass-less and inextensible. If the second bob, after collision acquires the minimum speed required to complete a full circle in the vertical plane, the ratio l1l2 isView Solution


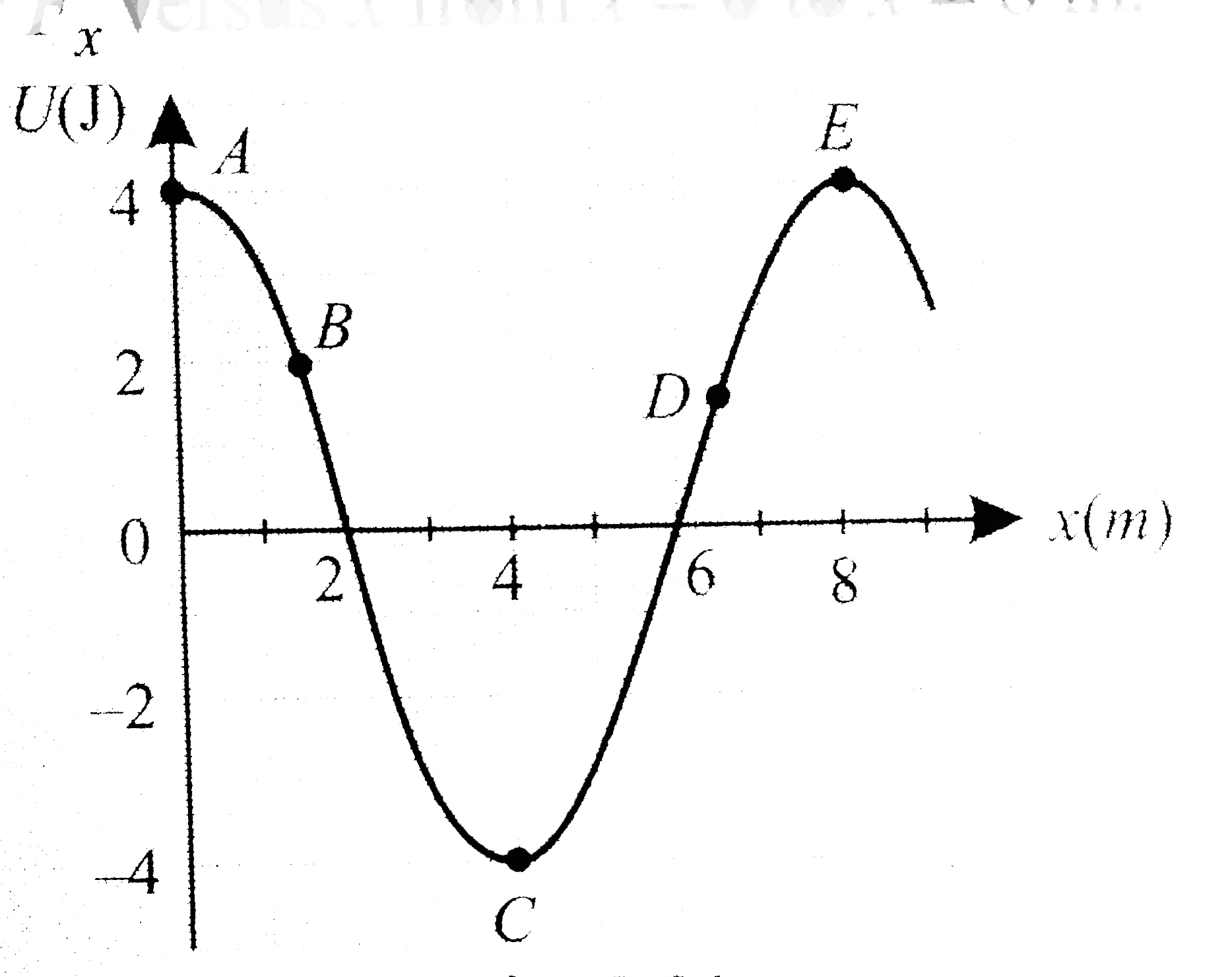








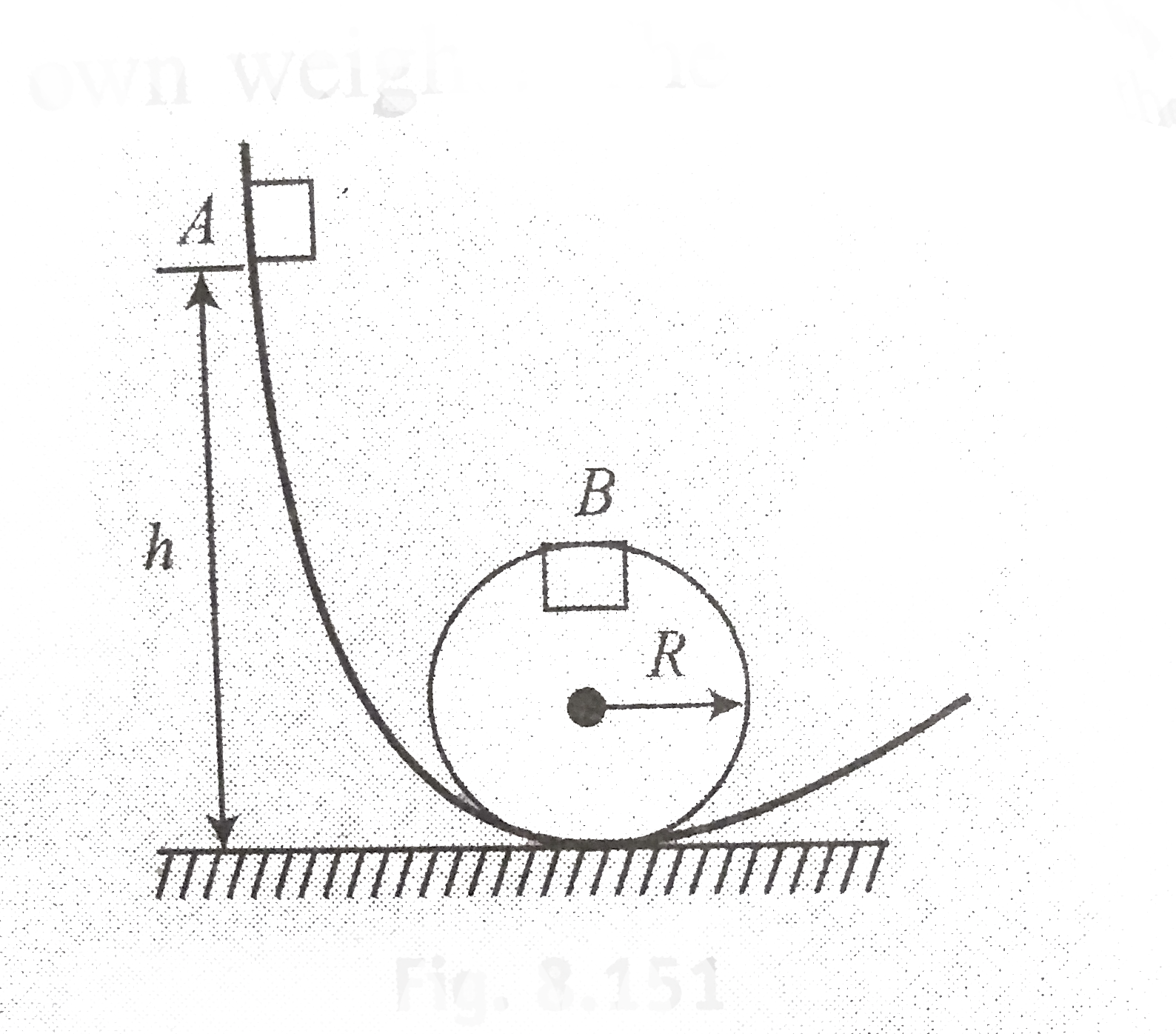

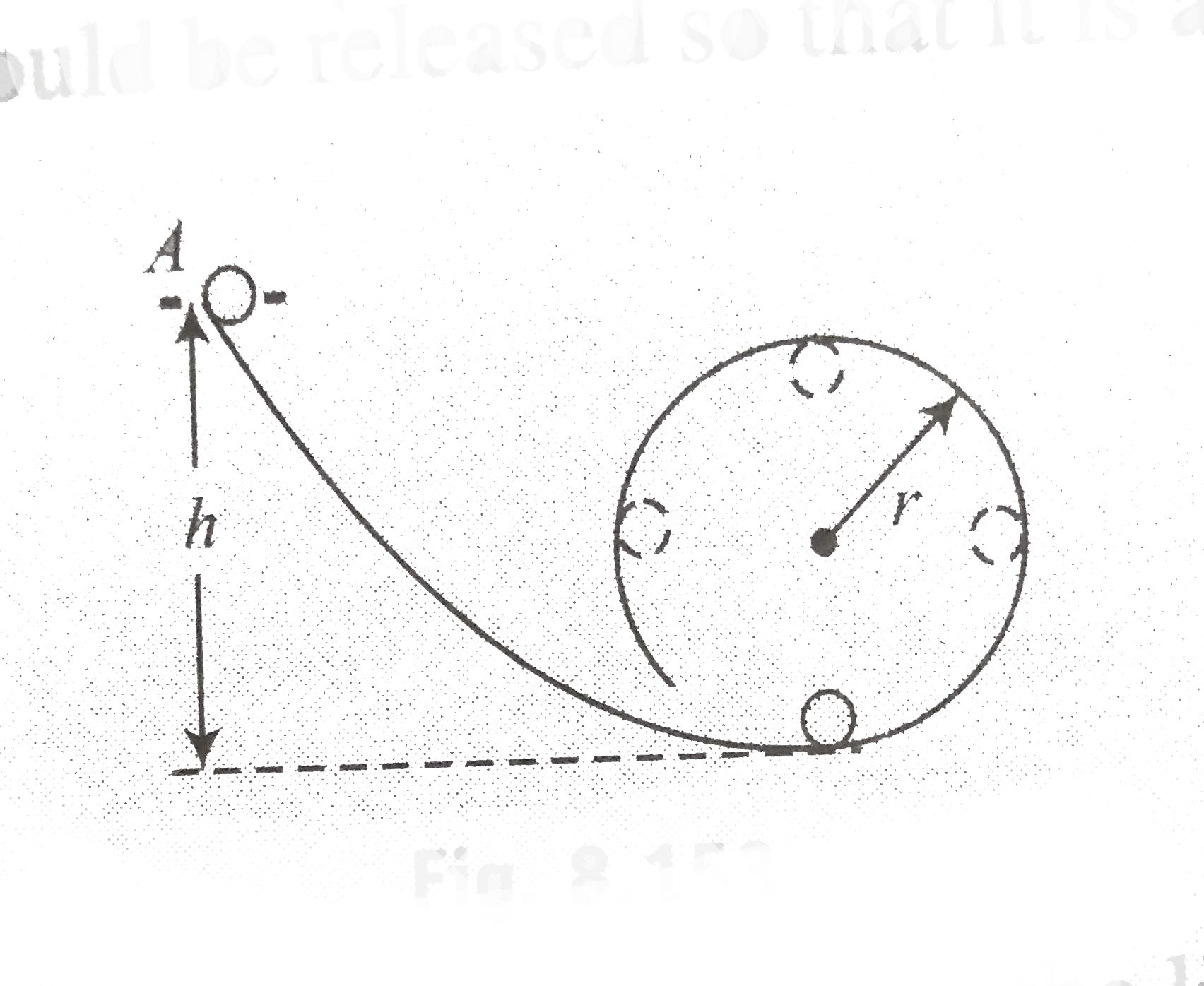

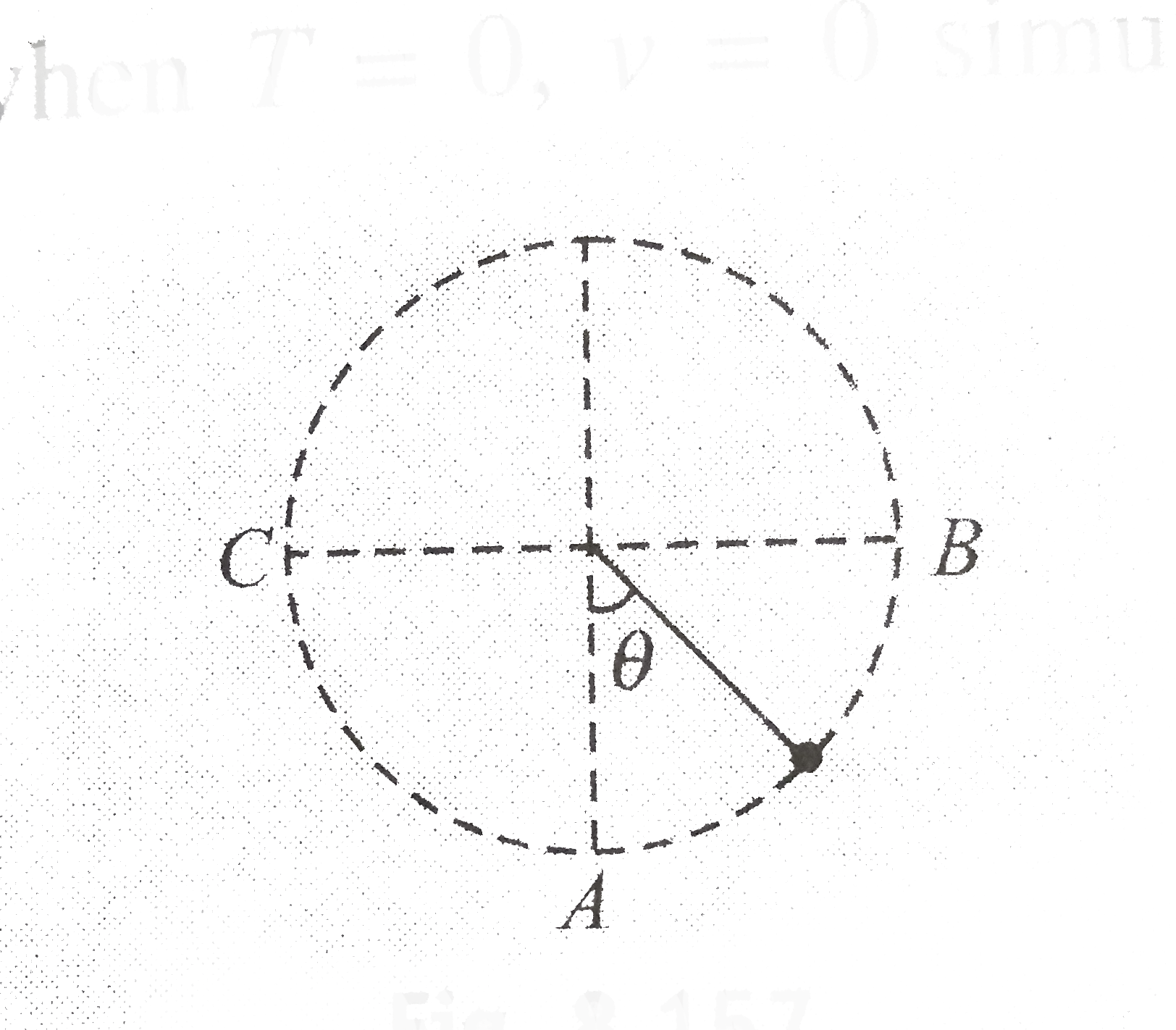



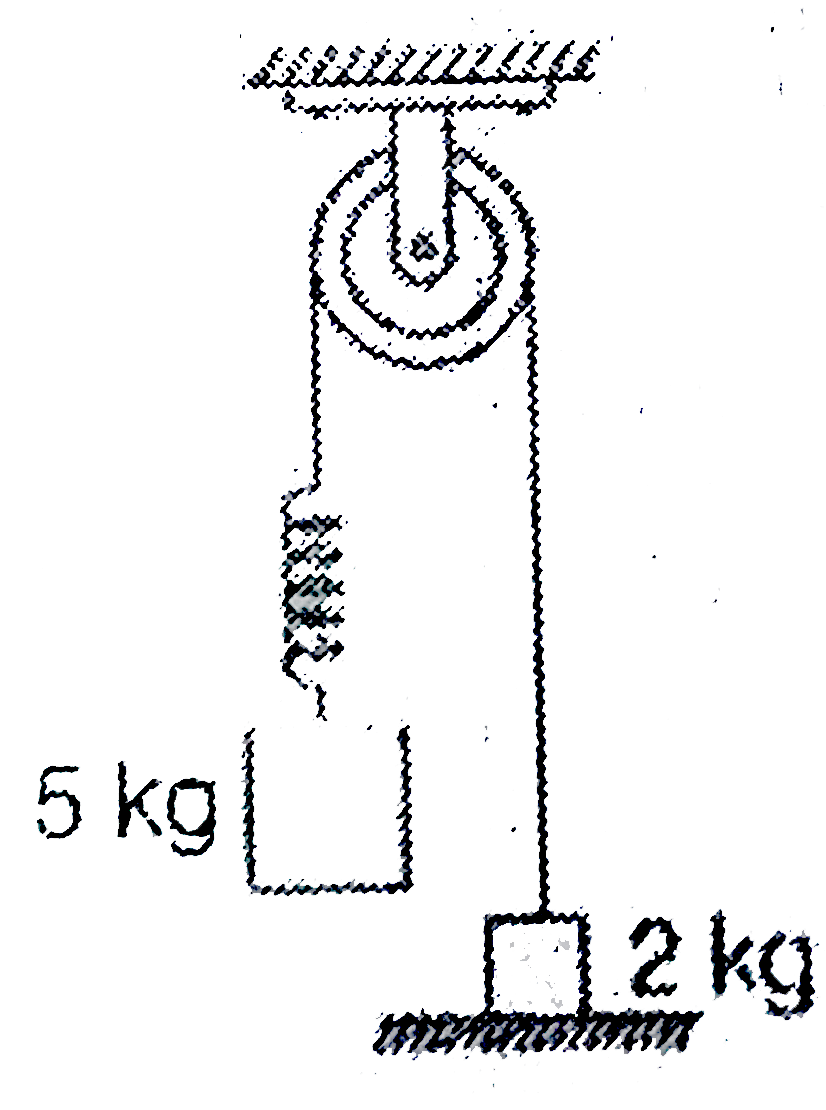
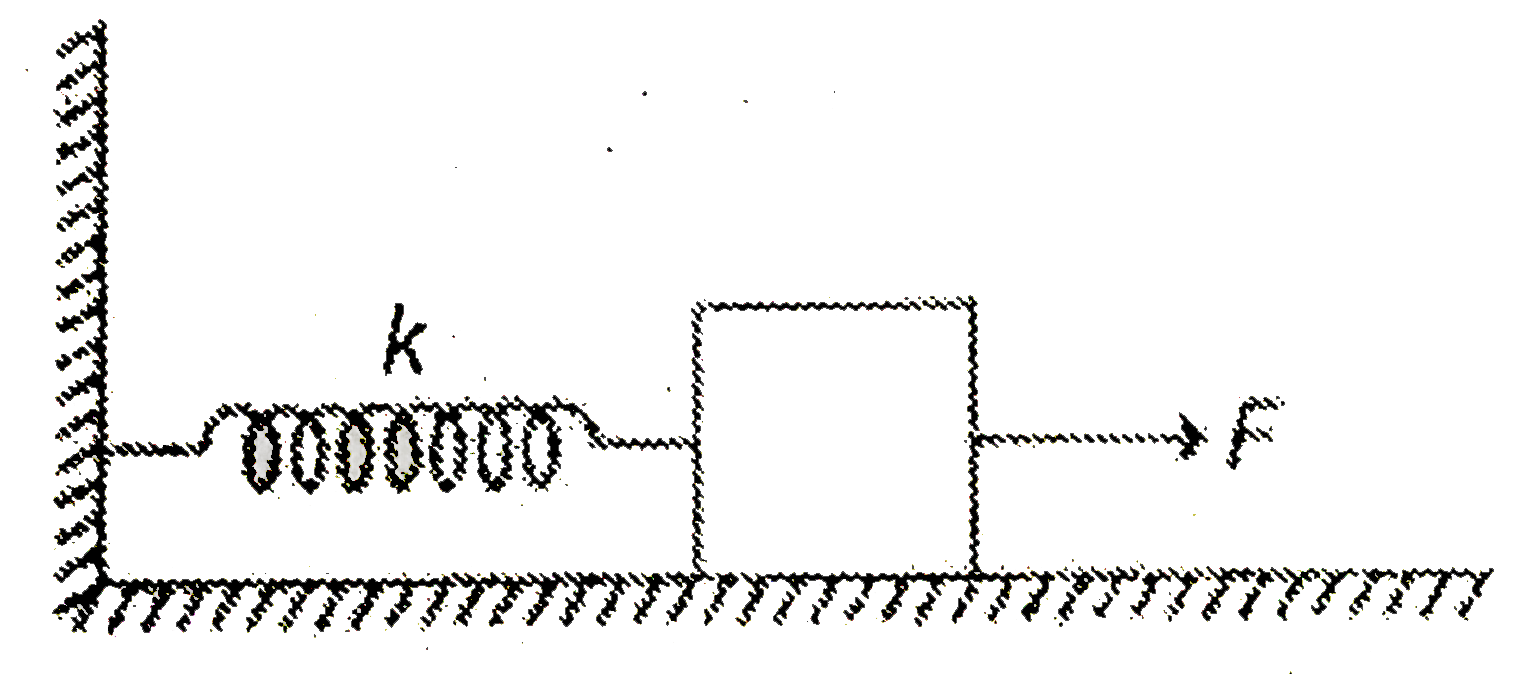

 .
.