Complete Solutions to SHORT ANSWER QUESTIONS of chapter ELECTROSTATIC POTENTIAL AND CAPACITANCE of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTROSTATIC POTENTIAL AND CAPACITANCE |
| U-LIKE SERIES | SHORT ANSWER QUESTIONS |
| Number Of Questions | 48 |
| Academic Year | 2023-24 |
Find an expression for the potential at a point due to a point charge Q.
View SolutionHow does electric potential vary from point to point due to a thin charged spherical shell ? Draw a graph showing variation of potential with distance.
View SolutionTwo spherical conductors of radii R, and R2 (R2 > Ri) are charged. If they are connected by a conducting wire, find out the ratio of the surface charge densities on them.
View SolutionDraw a plot showing the variation of (i) electric field E, and (ii) electric potential V with distance 'r' due to a point charge Q.
View SolutionDerive an expression for the electric potential at any point along the axial line of an electric dipole.
View SolutionDeduce an expression for the electric potential due to an electric dipole at any point on its axis. Mention one contrasting feature of electric potential at a point due to dipole as compared to that due to a single charge.
View SolutionShow mathematically that the potential at a point on the equatorial line of an electric dipole is zero.
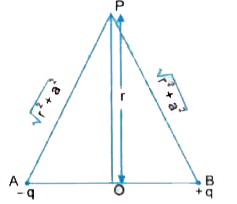
View SolutionDerive an expression for the work done in rotating an electric dipole of dipole moment 'p' in a uniform electric field 'E' from an orientation `theta_1" to " theta_2`.
View SolutionA dipole is present in an electrostatic field of magnitude `10^6 NC^(-1)`. If the work done in rotating it from its position of stable equilibrium to its positionof unatable equilibriumequals `2 xx 10^(-23) J`,find the magnitude of the dipole moment of this dipole.
View SolutionCalculate the amount of work done in turing an electric dipole of dipole moment `2 xx 10^(-8) C -m` from its position of unstable eqquilibrium to its position of stable equilibrium, in a uniform electric field of `10^3` N `C^(1)`.
View SolutionThe electric field and electric potential at any point due to a point charge kept in air si `20 N C^(-1)` and `10 J C^(-1)` respectively. Compute the magnitude of this charge.
View SolutionCalculate the electric potetial at the surface of a gold nucles. Given, the radius of nucleus `= 6.6 xx 10^(-15)` m and atomic number of gold = 79.
View SolutionThe following data was obtained for the dependence of the magnitude of the electric field, with distance,form a refernce point O, within the chargedistribution in the shaded region figure.

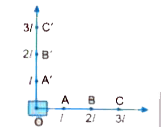
(i) Identify the charge distribution and justify your answer.
(ii) If the potential due to this charge distribution, has a value V at the point A, what is its value at the point A'?
View SolutionA test charge 'q' is moved without acceleration from A to C along the path from A to B and then from B to C in electric field E as shows in the figure. (i) Calculate the potential difference between A and C. (ii) At which point (of the two) is the electric potential more and why ?

View SolutionAn electric dipole is held in a uniform electric field.
Show that the net force acting on it is zero.
View SolutionAn electric dipole is held in a uniform electric field.
The dipole is aligned parallel to the field.Find the work done is rotating it through the angle of `180^@`.
View SolutionWhat is an equipotential surface ? Show that the electric field at a point on the surface of a charged conductor or just outside it is perpendicular to the surface ?
View SolutionState main characteristics of an equipotential surface.
View SolutionCan two equipotential surfaces intersect each other? Give reasons.
View SolutionTwo charges - q and + q are located at points A(0, 0, -a) and B(0, 0, +a) respectively. How much work is done in moving a test charge from point P(7,0,0) to Q(-3,0,0) ?
View SolutionDraw 3 equipotential surfaces corresponding to a field that uniformly increases in magnitude but remains constant along Z-direction. How are these surfaces different from that of a constant electric field along Z-direction ?
View SolutionDraw the equipotential surfaces due to an electric dipole. Locate the points where potential due to the dipole is zero.
View Solutionwo uniformly large parallel thin plates having charge densities `+sigma and - sigma` are kept in the X-Z plane at a distance 'd' apart. Sketch an equipotential surface due to electric field between the plates. If a particle of mass m and charge'- q' remains stationary between the plates, what is the magnitude and direction of this field ?
View SolutionTwo point charges `10 muC and -10 muC` are separated by a distance of 40 cm in air.
Calculate the electrostatic potential energy of the system, assuming the zero of the potential energy to be at infinity.
View SolutionTwo point charges `10 muC and -10 muC` are separated by a distance of 40 cm in air.
Draw an equipotential surface of the system.
View SolutionTwo point charges ` + 4 muC and -2 muC` are separated by a distance of 1 m in air. Calculate at what point on the line joining the two charges is the electric potential zero.
View SolutionTwo point charges, `q_1 = 10 xx 10^(-8) C and q_2 = -2 xx 10^(-8) C`, are separated by a distance of 60 cm in air.
Find at what distance from the 1st charge `q_1`, would the electric potential be zero.
View SolutionTwo point charges, `q_1 = 10 xx 10^(-8) C and q_2 = -2 xx 10^(-8) C`, are separated by a distance of 60 cm in air.
Also calculate the electrostatic potential energy of the system.
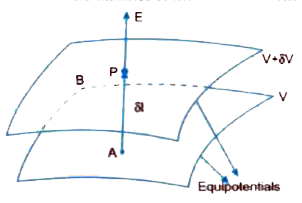
View SolutionTwo closely spaced equipotential surfaces A and B with potentials V and `V + deltaV` (where SV is the change in V) are kept 8l distance apart as shown in the Fig. Deduce the relation between the electric field and the potential gradient between them. Write the two important conclusions concerning the relation between the electric field and the electric potential.
View SolutionDerive an expression for the potential energy of an electric dipole of dipole moment `vecp` in an electric field `vecE`.
View SolutionCalculate the amount of work done to dissociate a system of three charges of `1muC, 1muC and -4 muC` placed on the vertices of an equilateral triangle of side 10 cm.
View SolutionIn a quark model of elementary particles, a neutron is made of one up quark (charge `=2/3e`) and two down quarks (charges `=1/3e`). Assume that they have a triangle configuration with side length of the order of `10^(-15)m.` Calculate electrostatic potential energy of neutron.
View SolutionExplain the working principle of a parallel plate capacitor.
View SolutionDefine dielectric constant of a medium. Briefly explain why the capacitance of a parallel plate capacitor increases, on introducing a dielectric medium between the plates.
View SolutionDerive an expression for the energy stored in a charged parallel plate capacitor.
View SolutionNet capacitance of three identical capacitors in series is `1 muF`. What will be their net capacitance if connected in parallel ?
Find the ratio of energy stored in the two configurations if they are both connected to the same source.
View SolutionTwo identical capacitors of 12 pF each are connected in series across a 50 V battery. Calculate the electrostatic energy stored in the combination. If these were connected in parallel across the same battery, find out the value of the energy stored in this combination.
View SolutionFind the ratio of the potential differences that must be applied across the parallel and series combination of two capacitors `C_1 and C_2` with their capacitances in the ratio 1 : 2 so that the energy stored in the two cases becomes the same.
View SolutionFind equivalent capacitance between A and B in the combination given below. Each capacitor is of `2 muF` capacitance.

View SolutionIf a.b.c source of 7V is connected across AB, how much charge is drawn from the source and what is the energy stored in the network ?
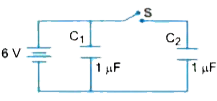
View SolutionFigure shows two idential capacitors, `C_1 and C_2`, each of `1mu F` capacitance connected to a battery of 6 V. Initially switch 'S' is closed. After sometime 'S' is left open and dielectric slabs of dielectric constant K = 3 are inserted to fill completely the space between the plates of the two capacitors. How will the (i) charge and (ii) potential difference between the plates of the capacitors be affected after the slabs are inserted?
View SolutionTwo capacitors of capacitance of `6 muF and 12 muF` are connected in series with a battery. The voltage across the `6 muF` capacitor is 2 V.Compute the total battery voltage.
View SolutionA network of four capacitors, each of capacitance `15muF`,is connected across a battery of 100 V as shown in the figure. Find the net capacitance and the charge on the capacitor `C_4`.
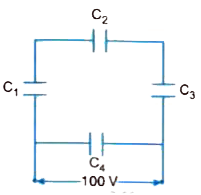
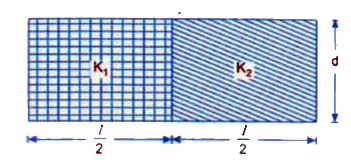
View SolutionTwo dielectric slabs of dielectric constants `K_1 and K_2` are filled in between the two plates, each of area A, of the parallel plate capacitor as shown in the figure. Find the net capacitance of the capacitor.
View SolutionA parallel plate capacitor of capacitance C is charged to a potential V. It is then connected to another uncharged capacitor having the same capacitance. Find out the ratio of the electrostatic energy stored in the combined system to that stored initially in the single capacitor.
View SolutionA slab of material of dielectric constant K has the same area as that of the plates of a parallel plate capacitor but has the thickness d/2, where d is the separation between the plates. Find out the expression for its capacitance when the slab is inserted between the plates of the capacitor.
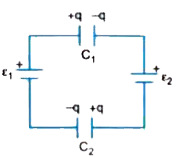
View SolutionDetermine the potential difference across the plates of the capacitor `C_1` of the network shown in the Fig. Assume `epsi_1 gt epsi_2`.
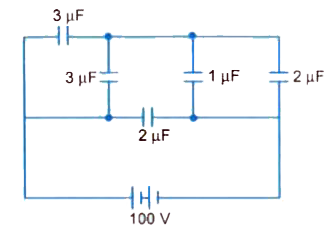
View SolutionThe figure shows a network of five capacitors connected to a 100 V supply, Calculate the total energy stored in the network.
View Solution
SHORT ANSWER QUESTIONS questions and complete solutions for chapter ELECTROSTATIC POTENTIAL AND CAPACITANCE of U-LIKE PHYSICS (HINGLISH) of Class 12