Complete Solutions to CASE BASED/SOURCE-BASED INTEGRATED QUESTIONS of chapter ELECTROSTATIC POTENTIAL AND CAPACITANCE of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTROSTATIC POTENTIAL AND CAPACITANCE |
| U-LIKE SERIES | CASE BASED/SOURCE-BASED INTEGRATED QUESTIONS |
| Number Of Questions | 18 |
| Academic Year | 2023-24 |
On the basis of your understanding of the following paragraph and the related studied concepts.
An electric dipole is a pair of equal and opposite point charges q and -9 separated by a distance '2a'. The total charge of the electric dipole is obviously zero but the field of the electric dipole at a point is non-zero because electric fields due to + qand - q charges at the point do not exactly cancel out. Electric field of a dipole, at large distances, depends on the product 'qa'. So we define a term dipole moment vector `vecp` of an electric dipole as `vecp = q(2a)` and its direction is along the line from q to + q charge. The dipole field at large distances fall off as `1/r^3`. Further, the magnitude and direction of the dipole field depends not only on the distance r but also on the angle between the position vector `vecr` and the dipole moment `vecp`.
Concept of electric dipoles is very significant for different materials. In most molecules, the centres of positive charges and of negative charges exactly coincide and their dipole moment is zero. However they develop a dipole moment when an electric field as applied. Such molecules are termed non-polar molecules. But in some molecules, the centres of positive charges do not exactly coincide with that of negative charges and the molecules has a permanent dipole moment even in the absence of an electric field. Such molecules are called polar molecules. Various materials give rise to interesting properties and important applications in the presence or absence of electric field.
Is the electric field due to a charge configuration with total charge zero necessarily zero ? Give an illustration in support of your answer.
View SolutionOn the basis of your understanding of the following paragraph and the related studied concepts.
An electric dipole is a pair of equal and opposite point charges q and -9 separated by a distance '2a'. The total charge of the electric dipole is obviously zero but the field of the electric dipole at a point is non-zero because electric fields due to + qand - q charges at the point do not exactly cancel out. Electric field of a dipole, at large distances, depends on the product 'qa'. So we define a term dipole moment vector `vecp` of an electric dipole as `vecp = q(2a)` and its direction is along the line from q to + q charge. The dipole field at large distances fall off as `1/r^3`. Further, the magnitude and direction of the dipole field depends not only on the distance r but also on the angle between the position vector `vecr` and the dipole moment `vecp`.
Concept of electric dipoles is very significant for different materials. In most molecules, the centres of positive charges and of negative charges exactly coincide and their dipole moment is zero. However they develop a dipole moment when an electric field as applied. Such molecules are termed non-polar molecules. But in some molecules, the centres of positive charges do not exactly coincide with that of negative charges and the molecules has a permanent dipole moment even in the absence of an electric field. Such molecules are called polar molecules. Various materials give rise to interesting properties and important applications in the presence or absence of electric field.
In which direction is the magnitude of electric field due to a short dipole (i) maximum, (ii) minimum ? Write expression for the same.
View SolutionOn the basis of your understanding of the following paragraph and the related studied concepts.
An electric dipole is a pair of equal and opposite point charges q and -9 separated by a distance '2a'. The total charge of the electric dipole is obviously zero but the field of the electric dipole at a point is non-zero because electric fields due to + qand - q charges at the point do not exactly cancel out. Electric field of a dipole, at large distances, depends on the product 'qa'. So we define a term dipole moment vector `vecp` of an electric dipole as `vecp = q(2a)` and its direction is along the line from q to + q charge. The dipole field at large distances fall off as `1/r^3`. Further, the magnitude and direction of the dipole field depends not only on the distance r but also on the angle between the position vector `vecr` and the dipole moment `vecp`.
Concept of electric dipoles is very significant for different materials. In most molecules, the centres of positive charges and of negative charges exactly coincide and their dipole moment is zero. However they develop a dipole moment when an electric field as applied. Such molecules are termed non-polar molecules. But in some molecules, the centres of positive charges do not exactly coincide with that of negative charges and the molecules has a permanent dipole moment even in the absence of an electric field. Such molecules are called polar molecules. Various materials give rise to interesting properties and important applications in the presence or absence of electric field.
Distinguish between polar and non-polar molecules. Give examples too.
View SolutionOn the basis of your understanding of the following paragraph and the related studied concepts.
An electric dipole is a pair of equal and opposite point charges q and -9 separated by a distance '2a'. The total charge of the electric dipole is obviously zero but the field of the electric dipole at a point is non-zero because electric fields due to + qand - q charges at the point do not exactly cancel out. Electric field of a dipole, at large distances, depends on the product 'qa'. So we define a term dipole moment vector `vecp` of an electric dipole as `vecp = q(2a)` and its direction is along the line from q to + q charge. The dipole field at large distances fall off as `1/r^3`. Further, the magnitude and direction of the dipole field depends not only on the distance r but also on the angle between the position vector `vecr` and the dipole moment `vecp`.
Concept of electric dipoles is very significant for different materials. In most molecules, the centres of positive charges and of negative charges exactly coincide and their dipole moment is zero. However they develop a dipole moment when an electric field as applied. Such molecules are termed non-polar molecules. But in some molecules, the centres of positive charges do not exactly coincide with that of negative charges and the molecules has a permanent dipole moment even in the absence of an electric field. Such molecules are called polar molecules. Various materials give rise to interesting properties and important applications in the presence or absence of electric field.
What do you mean by polarisation of a dielectric ?
View SolutionOn the basis of your understanding of the following paragraph and the related studied concepts.
An electric dipole is a pair of equal and opposite point charges q and -9 separated by a distance '2a'. The total charge of the electric dipole is obviously zero but the field of the electric dipole at a point is non-zero because electric fields due to + qand - q charges at the point do not exactly cancel out. Electric field of a dipole, at large distances, depends on the product 'qa'. So we define a term dipole moment vector `vecp` of an electric dipole as `vecp = q(2a)` and its direction is along the line from q to + q charge. The dipole field at large distances fall off as `1/r^3`. Further, the magnitude and direction of the dipole field depends not only on the distance r but also on the angle between the position vector `vecr` and the dipole moment `vecp`.
Concept of electric dipoles is very significant for different materials. In most molecules, the centres of positive charges and of negative charges exactly coincide and their dipole moment is zero. However they develop a dipole moment when an electric field as applied. Such molecules are termed non-polar molecules. But in some molecules, the centres of positive charges do not exactly coincide with that of negative charges and the molecules has a permanent dipole moment even in the absence of an electric field. Such molecules are called polar molecules. Various materials give rise to interesting properties and important applications in the presence or absence of electric field.
Define polarisation vector and give its SI unit.
View SolutionOn the basis of your understanding of the following paragraph and the related studied concepts.
An equipotential surface is a surface with a constant value of electric potential at all points on the surface. The component of electric field parallel to an equipotential surface is zero, as the potential does not change in this direction. Thus, the electric field is perpendicular to the equipotential surface at each point of the surface. Further, say the direction of electric field electrical potential gradually fall with distance.
Draw equipotential surfaces around an isolated positive point charge + q. Mark direction of electric field `vecE` also.
View SolutionOn the basis of your understanding of the following paragraph and the related studied concepts.
An equipotential surface is a surface with a constant value of electric potential at all points on the surface. The component of electric field parallel to an equipotential surface is zero, as the potential does not change in this direction. Thus, the electric field is perpendicular to the equipotential surface at each point of the surface. Further, say the direction of electric field electrical potential gradually fall with distance.
A uniform electric field `vecE = 1000 hati V m^(-1)` exists in space at a given place. What is the shape of equipotential surfaces there ?
View SolutionOn the basis of your understanding of the following paragraph and the related studied concepts.
An equipotential surface is a surface with a constant value of electric potential at all points on the surface. The component of electric field parallel to an equipotential surface is zero, as the potential does not change in this direction. Thus, the electric field is perpendicular to the equipotential surface at each point of the surface. Further, say the direction of electric field electrical potential gradually fall with distance.
If electric potential at origin point O be 100 V, then for electric field specified in part (b), draw equipotential surfaces corresponding to potentials 80 V, 60 V and 40 V respectively.
View SolutionOn the basis of your understanding of the following paragraph and the related studied concepts.
An equipotential surface is a surface with a constant value of electric potential at all points on the surface. The component of electric field parallel to an equipotential surface is zero, as the potential does not change in this direction. Thus, the electric field is perpendicular to the equipotential surface at each point of the surface. Further, say the direction of electric field electrical potential gradually fall with distance.
Four equipotential surfaces are shown in the adjoining figure. Find the magnitude and direaction of the electric field.

View SolutionOn the basis of your understanding of the following paragraph and the related studied concepts.
An equipotential surface is a surface with a constant value of electric potential at all points on the surface. The component of electric field parallel to an equipotential surface is zero, as the potential does not change in this direction. Thus, the electric field is perpendicular to the equipotential surface at each point of the surface. Further, say the direction of electric field electrical potential gradually fall with distance.
If a charge of 2 nC is taken from equipotential surface number 2 to 3, what is the amount of work done ?
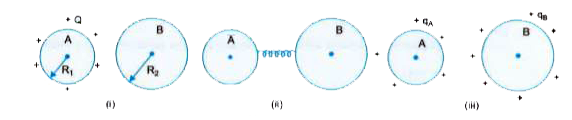
View SolutionSee the figure here. We have two hollow thin spherical shells A and B of radii R, and R, respectively. Initially as shown in Fig. (i) shell B has a charge + Q which is uniformly distributed over its outer surface but shell B has no charge. At a particular instant the two spherical shells are connected by a thin copper wire as shown in Fig. (ii). After a couple of minutes two spherical shells A and B are disconnected again as shown in Fig. (iii).

Now answer the following questions :
What is the ratio of capacitances of shell A and shell B ?
View SolutionSee the figure here. We have two hollow thin spherical shells A and B of radii R, and R, respectively. Initially as shown in Fig. (i) shell B has a charge + Q which is uniformly distributed over its outer surface but shell B has no charge. At a particular instant the two spherical shells are connected by a thin copper wire as shown in Fig. (ii). After a couple of minutes two spherical shells A and B are disconnected again as shown in Fig. (iii).

Now answer the following questions :
What is the ratio of final electric potentials of shell A and shell B ?
View SolutionSee the figure here. We have two hollow thin spherical shells A and B of radii R, and R, respectively. Initially as shown in Fig. (i) shell B has a charge + Q which is uniformly distributed over its outer surface but shell B has no charge. At a particular instant the two spherical shells are connected by a thin copper wire as shown in Fig. (ii). After a couple of minutes two spherical shells A and B are disconnected again as shown in Fig. (iii).

Now answer the following questions :
Find the ratio of surface charge densities of shell A and shell B.
View SolutionSee the figure here. We have two hollow thin spherical shells A and B of radii R, and R, respectively. Initially as shown in Fig. (i) shell B has a charge + Q which is uniformly distributed over its outer surface but shell B has no charge. At a particular instant the two spherical shells are connected by a thin copper wire as shown in Fig. (ii). After a couple of minutes two spherical shells A and B are disconnected again as shown in Fig. (iii).

Now answer the following questions :
Find the ratio of electric field on the surfaces of shell A and B.
View SolutionSee the figure here. We have two hollow thin spherical shells A and B of radii R, and R, respectively. Initially as shown in Fig. (i) shell B has a charge + Q which is uniformly distributed over its outer surface but shell B has no charge. At a particular instant the two spherical shells are connected by a thin copper wire as shown in Fig. (ii). After a couple of minutes two spherical shells A and B are disconnected again as shown in Fig. (iii).
Now answer the following questions :
Compare the final electrostatic energy stored in shell A with that in shell B.
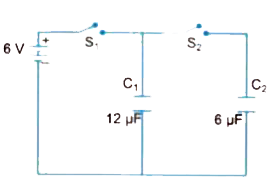
View SolutionWe have two capacitors `C_1 and C_2` of capacitance `12 muF` and `6 muF` respectively. As shown in the given circuit arrangement the two capacitors are joined to a power supply of 6 volts. Initially the switch `S_1` is closed but switch `S_2` is open. After some time, the switch `S_1` is opened and simultaneously switch `S_2` is closed.
Now answer the following questions :
The final value of potential of capacitor `C_1` is
View SolutionWe have two capacitors `C_1 and C_2` of capacitance `12 muF` and `6 muF` respectively. As shown in the given circuit arrangement the two capacitors are joined to a power supply of 6 volts. Initially the switch `S_1` is closed but switch `S_2` is open. After some time, the switch `S_1` is opened and simultaneously switch `S_2` is closed.
Now answer the following questions :
The final value of charge on capacitor `C_2` is
View SolutionWe have two capacitors `C_1 and C_2` of capacitance `12 muF` and `6 muF` respectively. As shown in the given circuit arrangement the two capacitors are joined to a power supply of 6 volts. Initially the switch `S_1` is closed but switch `S_2` is open. After some time, the switch `S_1` is opened and simultaneously switch `S_2` is closed.
Now answer the following questions :
The fractional loss in electrostatic energy of the arrangement after closing the switch `S_2` is
View Solution
CASE BASED/SOURCE-BASED INTEGRATED QUESTIONS questions and complete solutions for chapter ELECTROSTATIC POTENTIAL AND CAPACITANCE of U-LIKE PHYSICS (HINGLISH) of Class 12