Complete Solutions to LONG ANSWER QUESTIONS-I of chapter ELECTROSTATIC POTENTIAL AND CAPACITANCE of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTROSTATIC POTENTIAL AND CAPACITANCE |
| U-LIKE SERIES | LONG ANSWER QUESTIONS-I |
| Number Of Questions | 64 |
| Academic Year | 2023-24 |
Two point charges `q_(1) , q_(2)` initially at infinity are brought one by one points `P_1` and `P_2` specified by position vectors `r_1` and `r_2` , relative to some origin . What is the potential energy of this energy configuration ?
View SolutionCalculate the electrostatic potential energy of a system of three point charges `q_(1) , q_2` and `q_(3)` located respectively at `vecr_(1) , vecr_(2)` and `vecr_(3)` with respect to a common origin O.
View SolutionDepict the equipotential surfaces for a system of two identical positive point charges placed a distance 'd' apart.
View SolutionDeduce the expression for the potential energy of a system of two point charges `q_1` and `q_2` brought from infinity to the points `vecr_1` and `vecr_2` respectively in the presence of external electric field `vecE`.
View SolutionDefine the term electric potential due to a point charge .
Calculate the electric potential at the centre of a square , of side `sqrt2` m , having charges `100 mu C , -50 mu C , 20 mu C ` and `-60 mu C ` at the four corners of this square .
View SolutionFour point charges Q , q Q and q are placed at the corners of a square of side 'a' as shown in the Fig. Find the
resultant electric force on a charge Q
View SolutionFour point charges Q , q Q and q are placed at the corners of a square of side 'a' as shown in the Fig. Find the
potential energy of this system .
View SolutionThree point charges `q , -4q` and `2q` are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the Fig. Obtain the experssion for the magnitude of the resultant electric force acting on the charge q.
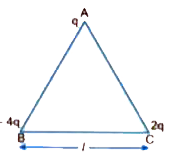
View SolutionFind out the amount of the work done to separate the charges at infinite distance .
View SolutionA charge Q is distributed over the surfaces of two concentric hollow spheres of radii r and `R ( R gt gt r)` , such that their surface charge densities are equal . Derive the expression for the potential at the common centre.
View SolutionThree concentric metallic shells A , B and C of radii a, b and c `(a lt b lt c)` have surface densities `+ sigma ,- sigma` and `+sigma` respectively as shown in Fig.
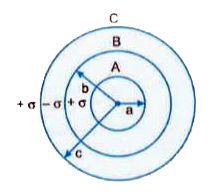
Obtain the expressions for the potential of three shells A , B and C .
View SolutionThree concentric metallic shells A , B and C of radii a, b and c `(a lt b lt c)` have surface densities `+ sigma ,- sigma` and `+sigma` respectively as shown in Fig.
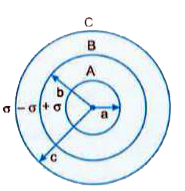
If shells A and C are at the same potential , obtain the relation between a , b and c.
View SolutionEstablish a relation for electric potential due to short dipole at a point distance r from the dipole along a line inclined at an angle `theta` from the dipole axis . Hence obtain value of electric potential at a point lying along (i) axial line , (ii) equatoral line of the dipole .
View SolutionExplain the underlying principle of working of a parallel plate capacitor .
If two similar plates , each of area A , having surface charge densities `+sigma` and `-sigma` are separated by a distance 'd' in air , write expression for :
the electric field at points between the plates .
View SolutionExplain the underlying principle of working of a parallel plate capacitor .
If two similar plates , each of area A , having surface charge densities `+sigma` and `-sigma` are separated by a distance 'd' in air , write expression for :
the potential difference between the plates.
View SolutionExplain the underlying principle of working of a parallel plate capacitor .
If two similar plates , each of area A , having surface charge densities `+sigma` and `-sigma` are separated by a distance 'd' in air , write expression for :
the capacitance of the capacitor so formed .
View SolutionFind an expression for the equivalent capacitance of a combination of three capacitors in series .
View SolutionDeduce an expression for the capacitance of a parallel plate capacitor having plate area 'A' and plate separation 'd'.
View SolutionObtain an expression for the capacitance of a combination of three capacitors in parallel .
View SolutionDeduce an expression for the electrostatic energy stored in a capacitance 'C' and having charge Q
How will the energy stored
View SolutionDeduce an expression for the electrostatic energy stored in a capacitance 'C' and having charge Q
How will the electric field inside capacitor be affected when it is completely filled with a dielectric material of dielectric constant K ?
View SolutionA parallel plate capacitor of capacitance C is charged to a potential V by a battery . Without disconnecting the battery , the distance between the plates is tripled and a dielectric medium of dielectric constant 10 is introduced between the plates of the capacitor . Explain giving reasons , how will the following be affected :
capacitance of the capacitor
View SolutionA parallel plate capacitor of capacitance C is charged to a potential V by a battery . Without disconnecting the battery , the distance between the plates is tripled and a dielectric medium of dielectric constant 10 is introduced between the plates of the capacitor . Explain giving reasons , how will the following be affected :
charge on the capacitor
View SolutionA parallel plate capacitor of capacitance C is charged to a potential V by a battery . Without disconnecting the battery , the distance between the plates is tripled and a dielectric medium of dielectric constant 10 is introduced between the plates of the capacitor . Explain giving reasons , how will the following be affected :
energy density of the capacitor .
View SolutionA parallel plate capacitor is charged by a battery . After sometime the battery is disconnected and a dielectric slab with its thickness equal to the plate separation is inserted between the plates . How will the capacitancee of the capacitor. ? Justify your answer
View SolutionA parallel plate capacitor is charged by a battery . After sometime the battery is disconnected and a dielectric slab with its thickness equal to the plate separation is inserted between the plates . How will potential difference between the plates ? Justify your answer
View SolutionA parallel plate capacitor is charged by a battery . After sometime the battery is disconnected and a dielectric slab with its thickness equal to the plate separation is inserted between the plates . How will the energy stored in the capacitor be affected ? Justify your answer
View SolutionA parallel plate capacitor , each with plate area A and separation d , is charged to a potential difference V . The battery used to charge it remains connected . A dielectric slab of thickness of and dielectric constant K is now placed between the plates . What change , if any , will take place in :
charge on plates ?
Justify your answer
View SolutionA parallel plate capacitor , each with plate area A and separation d , is charged to a potential difference V . The battery used to charge it remains connected . A dielectric slab of thickness of and dielectric constant K is now placed between the plates . What change , if any , will take place in :
electric filed intensity between the plates ? Justify your answer .
View SolutionA parallel plate capacitor , each with plate area A and separation d , is charged to a potential difference V . The battery used to charge it remains connected . A dielectric slab of thickness of and dielectric constant K is now placed between the plates . What change , if any , will take place in :
capacitance of the capacitor ? Justify your answer .
View SolutionA capacitor of unknown capacitance is connected across a battery of V volts . The charge stored in it is `360 mu C` . When potential across the capacitor is reduced by 120 V , the charge stored in it becomes 120 `mu C ` . Calculate :
The potential V and the unknown capacitance C .
View SolutionA capacitor of unknown capacitance is connected across a battery of V volts . The charge stored in it is `360 mu C` . When potential across the capacitor is reduced by 120 V , the charge stored in it becomes 120 `mu C ` . Calculate :
What will be the charge stored in the capacitor , if the voltage applied had increased by 120 V ?
View SolutionTwo capacitors of unknown capacitances `C_1` and `C_2` are connected first in series and then in parallel across a battery of 100 V . If the energy stored in the two combinations is 0.045 J and 0.25 J respectively , determine the value of `C_1` and `C_2` . Also calculate the charge on each capacitor in parallel combination .
View SolutionFind the total energy stored in the capacitors in the given network of Fig.
View SolutionThree identical capacitors `C_1 , C_2` and `C_3` of capacitance `6 mu F ` each are connected to a 12 V battery as shown in Fig
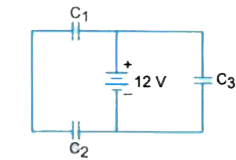
charge on each capacitor
View SolutionThree identical capacitors `C_1 , C_2` and `C_3` of capacitance `6 mu F ` each are connected to a 12 V battery as shown in Fig
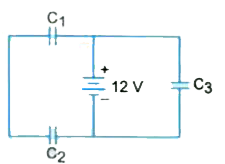
equivalent capacitance of the network
View SolutionThree identical capacitors `C_1 , C_2` and `C_3` of capacitance `6 mu F ` each are connected to a 12 V battery as shown in Fig
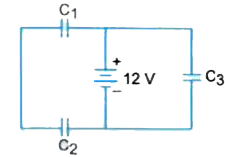
energy stored in the network of capacitors .
View SolutionTwo parallel plate capacitors X and Y have the same area of plates and same separation between them , X has air between the plates while Y contains a dielectric medium of `epsi_(r) = 4`.
Calculate capacitance of each capacitor if equivalent capacitance of the combination is `4 mu F `.
View SolutionTwo parallel plate capacitors X and Y have the same area of plates and same separation between them , X has air between the plates while Y contains a dielectric medium of `epsi_(r) = 4`.
Calculate the potential difference between the plates of X and Y.
View SolutionTwo parallel plate capacitors X and Y have the same area of plates and same separation between them , X has air between the plates while Y contains a dielectric medium of `epsi_(r) = 4`.
Estimate the ratio of electrostatic energy stored in X and Y .
View SolutionTwo identical capacitors of 12 pF each are connected in series across a battery of 50 V . How much electrostatic energy is stored in the combination ? If these were connected in parallel across the same battery , how much energy will be stored in the combination now ?
Also find the charge drawn from the battery in each case.
View SolutionTwo parallel plate capacitors of capacitances `C_1` and `C_2` such that `C_2 = 2 C_1` are connected across battery of V volts as shown in the Fig . Initially the key K is kept closed to fully charge the capacitors . The key K is now thrown open and dielectric slabs of dielectric constant `K_0` are inserted in the two capacitors to completely fill the gap between the plates .
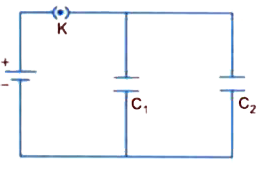
Find the ratio of the net capacitance
View SolutionTwo parallel plate capacitors of capacitances `C_1` and `C_2` such that `C_2 = 2 C_1` are connected across battery of V volts as shown in the Fig . Initially the key K is kept closed to fully charge the capacitors . The key K is now thrown open and dielectric slabs of dielectric constant `K_0` are inserted in the two capacitors to completely fill the gap between the plates .
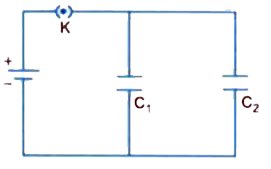
Find the ratio of the energies stored in the combination before and after the introduction of dielectric slabs .
View SolutionA 12 pF capacitor is connected to a 50 V battery . How much electrostatic energy is stored in the capacitor ? If another capacitor of 6 pF is connected in series with it with the same battery connected across the combination , find the charge stored and potential difference across each capacitor.
View SolutionCalculate the potential difference and the energy stored in the capacitor `C_2` in the circuit shown in the Fig. Given potential at A is 90 V , `C_1 = 20 mu F , C_2 = 30 mu F ` and `C_3 = 15 mu F `
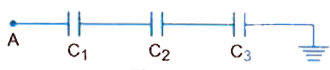
View SolutionThe equivalent capacitance of the combination between A and B in the given figure is `4 mu F ` .
Calculate capacitance of the capacitor C.

View SolutionThe equivalent capacitance of the combination between A and B in the given figure is `4 mu F ` .
Calculate charge on each capacitor if a 12 V battery is connected across terminals A and B .

View SolutionThe equivalent capacitance of the combination between A and B in the given figure is `4 mu F ` .
What will be the potential drop across each capacitor ?

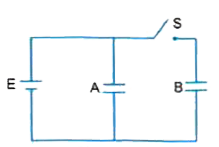
View SolutionTwo identical parallel plate capacitors A and B are connected to a battery of V volts with the switch S closed . The switch is now opened and the free space between the plates of the capacitors is filled with dielectric of dielectric constant K . Find the ratio of the total electrostatic energy stored in both capacitors before and after the introduction of the dielectric .
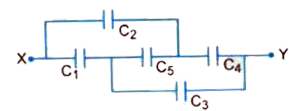
View SolutionFind the equivalent capacitance of the network shown in the fig , when each capacitor is of 1 `mu F` . When the ends X and Y are connected to a 6 V battery , find out (i) the charge and (ii) the energy stored in the network
View SolutionTwo metallic spheres of radii R and 2 R are charged so that both of these have same surface charge density `sigma`. If they are connected to each other with a conducting wire , in which direction will the charge flow and why ?
View SolutionA conducting slab of thickness 't' is introduced without touching between the plates of a parallel plate capacitor , separated by a distance 'd' `( t lt d) ` . Derive an expression for the capacitance of the capacitor .
View SolutionA dielectric slab of thickness 't' is kept between the plates of a parallel plate capacitor separated by a distance 'd' `(t lt d)` . Derive the expression for the capacity of the capacitor .
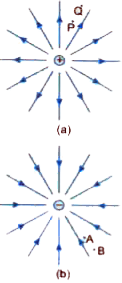
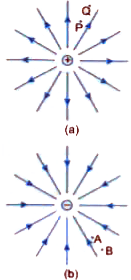
View SolutionFig (a) and (b) show the field lines of a single positive and negative charges respectively .
Give the signs of the potential difference : `V_(P) - V_(Q) , V_(B) - V_(A)`
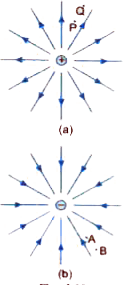
View SolutionFig (a) and (b) show the field lines of a single positive and negative charges respectively .
Give the sign of the potential energy difference of a small negative charge between the points Q and P , A and B .

View SolutionFig (a) and (b) show the field lines of a single positive and negative charges respectively .
Give the sign of the work done by the field in moving a small positive charge from Q to P .
View SolutionFig (a) and (b) show the field lines of a single positive and negative charges respectively .
Give the sign of the work done by an external agency in moving a small negative charge from B to A .
View SolutionFig (a) and (b) show the field lines of a single positive and negative charges respectively .
Does the kinetic energy of a small negative charge increase or decrease in going from B to A ?

View SolutionThe two plates of a parallel plate capacitor are 4 mm apart . A slab of dielectric constant 3 and thickness 3 mm is introduced between the plates with its face parallel to them . The distance between the plates is so adjusted that the capacity of the capacitor becomes `2/3` rd of its original value . What is the new distance the plates ?
View SolutionFind an expression for loss of electrical energy when two capacitors (or conductors ) maintained at different potential are allowed to share their charges .
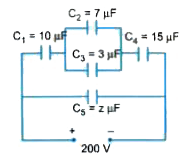
View SolutionA system of capacitors , connected as shown , has a total energy of 160 mJ stored in it . Obtain the value of the equivalent capacitance of this system and the value of x .
View SolutionA network of four capacitors each of 12 `mu F ` capacitance is connected to a 500 V supply as shown in the Fig .
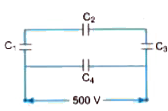
Determine equivalent capacitance of the network .
View SolutionA network of four capacitors each of 12 `mu F ` capacitance is connected to a 500 V supply as shown in the Fig .

Determine charge on each capacitor .
View SolutionFind the capacitance of the infinite ladder of capacitors shown in Fig between points A and B .
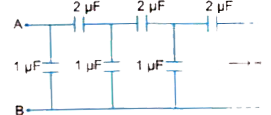
View Solution
LONG ANSWER QUESTIONS-I questions and complete solutions for chapter ELECTROSTATIC POTENTIAL AND CAPACITANCE of U-LIKE PHYSICS (HINGLISH) of Class 12