Complete Solutions to PROBLEMS of chapter MOTION IN A PLANE of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MOTION IN A PLANE |
| AAKASH SERIES | PROBLEMS |
| Number Of Questions | 29 |
| Academic Year | 2023-24 |
The speed with which a bullent can be fired is `150 ms^(-1)`. Calculate the greatest distance to which it can be projected and also the maximum height to which it would rise .
View SolutionThe horizontal range of a projectile is `2sqrt(3)` time its maximum height. Find the angle of projection .
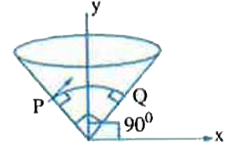
View SolutionA particle is projected from point P with velocity `5 sqrt(2)ms^(-1)` prependicular to the surface of a hollow right angle cone whose axis is vertical . It collides at Q normally. The time of the flight of the poarticle is .
View SolutionIf at point of projection , the velcoity of particle is "u" and is direction at an angle `alpha` to the horizontal , then show that it will be moving at right angles to the its initial direction after a time `((u "cosec" alpha))/(g)`
View SolutionIf `y = x - (1)/(2)x^(2)` is the equation of a trajectory , find the time of flight.
View SolutionIf R is the horizontal range for `theta` inclination and h is the maximum height reached by the projectile, show that the maximum ragne is given by `(R^(2))/(8h) + 2h`.
View SolutionA cannon and a target are 5.10Km apart and located at the same level. How soon will the shell launched with the initial velocity 240m/s reach the target in the absence of air drag?
View SolutionA hunter aims a gun at a monkey hanging from a tree some distance away. The monkey drops from the branch at the moment he fires the gun hoping to avoid the bullet. Explain why the monkey made a wrong move.
View SolutionA rifle with a muzzle velcity of `100 ms^(-1)` shots a bullet at a small target 30 m away in the same horizontal line. How much height above the target must the rifle be aimed so that the bullet will hit the taget ?
View SolutionA particle is projected from the ground with an initial speed of V at an angle of projection `theta`. The average velocity of the particle between its time of projection and time it reaches highest point of trajectory is
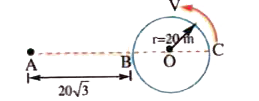
View SolutionA particle is moving along a vertical circle of radius r = 20 m with a constnat vertical circle of radius r = 20 m with a constnat speed v = 31.4m/s as shown is figure . Straight line ABC is horizontal and passes throught the centre of the circle . A shell if fired from point A at the instant when the particle is at C. If distance AB is `20sqrt(3)` m and the shell collide with the particle at B , then prove `tan theta = ((2 n -1)^(2))/(sqrt(3)) `.where n is an interger. Further , show that smallest value of `theta ` is `30^(@)`.
View SolutionThe path of a projectile is given by the equation `y = ax – bx^(2)`, where a and b are constants and x and y are respectively horizontal and vertical distances of projectile from the point of projection. The maximum height attained by the projectile and the angle of projection are respectively.
View SolutionA particle moves in the plane XY with constant accelenration a direction along the negative Y-axis . The equation of motion of the particle has the form , `y = Ax - Bx^(2)`. Where A and B are positive constants. Find the velcotiy of the particle at the origin of the coordinates.
View SolutionA stone is projected from the point of a ground in such a direction so as to hit a bird on the top of a telegraph post of height h and then attain the maximum height 2h above the ground . If at the instant of projection, the bird were to fly away horizontally with a unifrom speed. Find the ratio between the horizontal velocities of the bird and stone , if the stone still hits the brid while ascending .
View SolutionA projectile shot at angles of `45^(@)` above the horizontal strikes a buliding 30 m away at a point 15 m above the point of projection. Find : (a) the speed of projection . (b) the magnitude and direction of velocity of projectile when it strikes the building .
View SolutionA particle is projected from a point O with velocity u in a direction making an angle `alpha` upward with the horizontal. AT P , it is moving at right angles to its initial direction of projection . Its velocity at P is .
View SolutionA ball is thrown form the origin in the x - y plane with velocity 28.28m/s at an angle `45^(@)` to the x-axis. At the same instant a trolley also starts moving with uniform velocity of 10 m/s along the positive x-axis . Initially rear end of the trolley is located at 38m from the origin. Determine the time position at which the ball hits the trolley.
View SolutionA particle is projected with a velocity `bar(v) = ahat(i) + bhat(j)` . Find the radius of curvature of the trajectory of the particle at (i) point of projection (ii) highest point .
View SolutionA boy is standing inside a train moving with a constant velcoity of magnitude 10m/s. He throws a ball vetically up with in speed of 5m/s relative to the train . Find the radius of curvature of the path of the ball just at the time of projection .
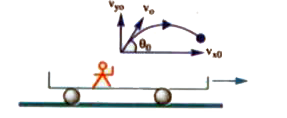
View SolutionA block of ice starts sliding down from the top of an inclined roof of a along a line of the greatest slope. The inclination of the roof with the horizontal is `30^(@)`. The heights of the highest and lowerst points of the roof are 8.1 m and 5.6 m respectively.At what horizontal distance from the lowest point will the block hit the ground ? Neglect air friction .`[g=9.8m//s^(2)]`.
View SolutionA particle is projected horizontally with a speed ''u'' rom the top of plane incline at an angle `theta` with the horizontal. How far from the point of projection will the particle strike the plane ?
View SolutionTwo particle move in a unifrom gravitational field with an acceleration "g". At the initial moment the paricles were located at one point and moved with velcoities `u_(1) = 3.0 ms^(-1)` and `u_(2) = 4.0 ms^(-1)` horizontally in opposite directions. Find the distance between the patricles at the moment when their their velocity vectors become mutually perpendicular .
View SolutionA ball rolls off the top of a stariway with a horizontal velocity magnitude 150 cm/sec. The steps are 20 cm high and 20 cm wide . Which step will the ball hit first ?
View SolutionTwo bodies are projected from the same point with equal speeds in such directions that they both strike the same point on a plane whose inclination is `beta`. If `alpha` the angle of projection of the first body with the horizontal , show that the ratio of their time of flights is `(sin (alpha - beta))/(cos alpha)`
View SolutionA particle projected with velcoity `v_(0)` strikes at right `alpha` plane through the point of projection .
View SolutionA body has maximum range `R_(1)` when projected up the inclined plane. The same body when projected down the inclined plane, it has maximum range `R_(2)`. Find its maximum horizontal inclined plane in the line of the greatest slope.
View SolutionA ball starts falling with zero initial velocity on a smooth inclined plane forming an angle a with the horizontal. Having fallen the distance h, the ball rebounds elastically off the inclined plane. At what distance from the impact point will the ball rebound for the second time?
View SolutionA cannon fires successively two shells with velocity `v_(0) = 250 m//s`, the first at the angle `therefore = 60^(@)` and the second at the angle `q_(2) = 45^(@)` to the horizontal, the azimuth being the same. Neglecting the air drag, find the time interval between firings leading to the collision of the shells.
View SolutionA particle A is projected with an initial velocity of 60 m/s at an angle `30^(@)` to the horizontal. At the same time a second particle B is projected in opposite direction with initial speed of 50 m/s from a A point at a distance of 100 m from A. If the particles collide in air, find (a) the angle of projection of particle B (b) timewhen the collisions takes place and (c) the distance of P from A. where collision occurs. `(g=10 m//s^(2))`

View Solution
PROBLEMS questions and complete solutions for chapter MOTION IN A PLANE of JEE (MAIN AND ADVANCED) PHYSICS of Class 12