Two particle move in a unifrom gravitational field with an acceleration "g". At the initial moment the paricles were located at one point and moved with velcoities u1=3.0ms−1 and u2=4.0ms−1 horizontally in opposite directions. Find the distance between the patricles at the moment when their their velocity vectors become mutually perpendicular .Solution in Telugu
The situation is shown fig.
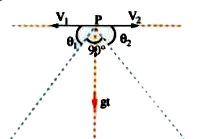
Let the velocity vectors perpendicular after time "t" when both particles has fallen same vertical distance 12>2 and have acquired same verticle velcoities gt.
Let the resultant velcoities makes angles θ1 and θ2 with horizontal.
Then tanθ1=gtv1andtanθ2=gtv2
Sicne velcoity vectors are perpendicular
θ1+θ2=90∘ hence θ2=cotθ1
It makes tanθ1=gtv1 and cotdθ1=gtv2
on mulitplying we get t=√v1v2g=andD=(u1+u2)t
Topper's Solved these Questions
- MOTION IN A PLANEBook:AAKASH SERIESChapter:MOTION IN A PLANEExercise:SHORT ANSWER TYPE QUESTIONS
Explore 6 Videos
- MOTION IN A PLANEBook:AAKASH SERIESChapter:MOTION IN A PLANEExercise:VERY SHORT ANSWER TYPE QUESTIONS
Explore 10 Videos
- MOTION IN A PLANEBook:AAKASH SERIESChapter:MOTION IN A PLANEExercise:EXERCISE-3 (Circular Motion)
Explore 7 Videos
- MOTION IN A STRAIGHT LINE Book:AAKASH SERIESChapter:MOTION IN A STRAIGHT LINE Exercise:very Short answer type question
Explore 15 Videos
Similar Questions
Show that the trajectory of an object thrown at certain angle with the horizontal is a parabola .
View SolutionWhat is the acceleration of a projectile at the top of its trajectory ?
View SolutionA particle ‘P is moving in a circle of radius "r" with uniform speed v. AB is the diameter of circle and 'C' is the centre. The angular velocity of P about A and C are in the ratio.
View SolutionGive two examples of the motion of big objects where the object can be treated as a particle and where it cannot be?
View SolutionTwo particles move in a uniform gravitational field with an acceleration g. At the initial moment the particles were located over a tower at one point and moved with velocities v_1 = 3m//s and v_2= 4m//s horizontally in opposite directions. Find the distance between the particles at the moment when their velocity vectors become mutually perpendicular.
View SolutionTwo particles move in a uniform gravitational field with an acceleration g .At the initial moment the particles were located at same point and moved with velocities u_(1)=9 ms^(-1) and u_(2)=4 ms^(-1) horizontally in opposite directions.The time between the particles at the moment when their velocity vectors are mutually perpendicular in s in (take g=10 ms^(-2) )
View SolutionTwo paricles A and B start simultaneously from the same point and move in a horizontal plane. A has an initial velocity u1 due east and acceleration a1 due north. B has an intial velocity u2 due north and acceleration a2 due east.
View SolutionA particle starts moving in +ve x direction with initial velocity of 10 ms^(-1) with a uniform acceleration of magnitude 2 ms^(-2) but directed in -ve x direction. What is the distance traversed by the particle in 12 seconds:
View SolutionTwo particles A and B start simultaneously from the same point and move in a horizontal plane. A has an initial velocity u1 due east and acceleration a1 due north. B has an initial velocity u2 due north and acceleration a2 due east. Then :
View SolutionTwo particles move in a uniform gravitational field with an acceleration g. At the intial moment the particles were located at one point and moved with velocity v_(1)=1" "ms^(-1)" and "v_(2)=4" "ms^(-1) horizontally in opposite directions. Find the time interval after their velocity vectors become mutually perpendicular
View SolutionTwo particle move in a unifrom gravitational field with an acceleration "g". At the initial moment the paricles were located at one point and moved with velcoities u1=3.0ms−1 and u2=4.0ms−1 horizontally in opposite directions. Find the distance between the patricles at the moment when their their velocity vectors become mutually perpendicular .
View SolutionTwo particles move in a uniform gravitational field with an acceleration "g". Al the initial moment the particles were located at same point and moved with velocities u1=0.8ms−1andu2=4.0ms−1 horizontally in opposite directions. Find the distance between the particles at the moment when their velocity vectors become mutually perpendicular. (g=10ms−2)
View SolutionVelocity of 5 molecules of gas is 4ms−1, 3 molecules is 10ms−1 and 6 molecules is 6ms−1, Then calculate uav,urms and ums.
View SolutionTwo particles move in a uniform gravitational field with an acceleration "g". At the initial moment the particles were located at same point and moved with velocities u_(1) = 0.8 ms^(-1) and u_(2) = 4.0 ms^(-1) horizontally in opposite directions. Find the distance between the particles at the moment when their velocity vectors become mutually perpendicular. (g = 10 ms^(-2))
View SolutionTwo particles move in a uniform gravitational field with an acceleration g. At the initial moment the particles were located at one point and moved with velocities u_(1)=3.0ms^(-1) and u_(2)=4.0ms^(-1) horizontally in opposite directions. Find the distance betwen the particles at the moment when their velocity vectors become mutually perpendicular.
View Solution

