Two particle move in a unifrom gravitational field with an acceleration "g". At the initial moment the paricles were located at one point and moved with velcoities u1=3.0ms−1 and u2=4.0ms−1 horizontally in opposite directions. Find the distance between the patricles at the moment when their their velocity vectors become mutually perpendicular .Solution in Telugu
t=√u1u2g,x=(u1+u2)t
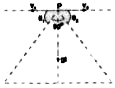
=0.48 m
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - SHORT ANSWER TYPE QUESTIONS
6 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
10 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-3 (Circular Motion)
7 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question
15 Videos
Similar Questions
Show that the trajectory of an object thrown at certain angle with the horizontal is a parabola .
View SolutionWhat is the acceleration of a projectile at the top of its trajectory ?
View SolutionA particle ‘P is moving in a circle of radius "r" with uniform speed v. AB is the diameter of circle and 'C' is the centre. The angular velocity of P about A and C are in the ratio.
View SolutionGive two examples of the motion of big objects where the object can be treated as a particle and where it cannot be?
View SolutionTwo particles move in a uniform gravitational field with an acceleration g. At the initial moment the particles were located over a tower at one point and moved with velocities v_1 = 3m//s and v_2= 4m//s horizontally in opposite directions. Find the distance between the particles at the moment when their velocity vectors become mutually perpendicular.
View SolutionTwo particles move in a uniform gravitational field with an acceleration g .At the initial moment the particles were located at same point and moved with velocities u_(1)=9 ms^(-1) and u_(2)=4 ms^(-1) horizontally in opposite directions.The time between the particles at the moment when their velocity vectors are mutually perpendicular in s in (take g=10 ms^(-2) )
View SolutionTwo paricles A and B start simultaneously from the same point and move in a horizontal plane. A has an initial velocity u1 due east and acceleration a1 due north. B has an intial velocity u2 due north and acceleration a2 due east.
View SolutionA particle starts moving in +ve x direction with initial velocity of 10 ms^(-1) with a uniform acceleration of magnitude 2 ms^(-2) but directed in -ve x direction. What is the distance traversed by the particle in 12 seconds:
View SolutionTwo particles A and B start simultaneously from the same point and move in a horizontal plane. A has an initial velocity u1 due east and acceleration a1 due north. B has an initial velocity u2 due north and acceleration a2 due east. Then :
View SolutionTwo particles move in a uniform gravitational field with an acceleration g. At the intial moment the particles were located at one point and moved with velocity v_(1)=1" "ms^(-1)" and "v_(2)=4" "ms^(-1) horizontally in opposite directions. Find the time interval after their velocity vectors become mutually perpendicular
View SolutionTwo particle move in a unifrom gravitational field with an acceleration "g". At the initial moment the paricles were located at one point and moved with velcoities u1=3.0ms−1 and u2=4.0ms−1 horizontally in opposite directions. Find the distance between the patricles at the moment when their their velocity vectors become mutually perpendicular .
View SolutionTwo particles move in a uniform gravitational field with an acceleration "g". Al the initial moment the particles were located at same point and moved with velocities u1=0.8ms−1andu2=4.0ms−1 horizontally in opposite directions. Find the distance between the particles at the moment when their velocity vectors become mutually perpendicular. (g=10ms−2)
View SolutionVelocity of 5 molecules of gas is 4ms−1, 3 molecules is 10ms−1 and 6 molecules is 6ms−1, Then calculate uav,urms and ums.
View SolutionTwo particles move in a uniform gravitational field with an acceleration "g". At the initial moment the particles were located at same point and moved with velocities u_(1) = 0.8 ms^(-1) and u_(2) = 4.0 ms^(-1) horizontally in opposite directions. Find the distance between the particles at the moment when their velocity vectors become mutually perpendicular. (g = 10 ms^(-2))
View SolutionTwo particles move in a uniform gravitational field with an acceleration g. At the initial moment the particles were located at one point and moved with velocities u_(1)=3.0ms^(-1) and u_(2)=4.0ms^(-1) horizontally in opposite directions. Find the distance betwen the particles at the moment when their velocity vectors become mutually perpendicular.
View Solution
