Complete Solutions to PROBLEM of chapter ELECTROMAGNETIC INDUCTION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTROMAGNETIC INDUCTION |
| AAKASH SERIES | PROBLEM |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
A rectangular loop of area 0.06 m2 is placed in a magnetic field of 0.3T with its plane (i) normal to the field (ii) inclined `30^(@)` to the field (iii) parallel to the field. Find the flux linked with the coil in each case.
View SolutionAt a certain location in the northern hemisphere, the earth.s magnetic field has a magnitude of `42 muT` and points downwards at `53^@` to the vertical. Calculate the flux through a horizontal surface of area `2.5 m^2. [sin 53^@ = 0.8]`

View SolutionThe magnetic flux through a coil perpendicular to its plane is varying according to the relation `phi_(B)= (5t^(3) +4t^(2) + 2t - 5)` weber. Calculate the induced current through the coil at t = 2 second. The resistance of the coil is 5 `Omega`.
View SolutionA circular coil of 500 turns of wire has an enclosed area of 0.1 `m^(2)` per turn. It is kept perpendicular to a magnetic field of induction 0.27 and rotated by `180^(@)` about a diameter perpendicular to the field in 0.1 s. How much charge will pass when the coil is connected to a galvanometer with a combined resistance of 50 `Omega`.
View SolutionSome magnetic flux is changed from a coil of resistance `10Omega` . As a result an induced current is developed in it, which varies with time as shown in figure. What is the magnitude of change in flux through the coil ?
View SolutionA tong solenoid with 15 turns per em has a small loop of area `2.0 cm^(2)` placed inside the solenoid normal to its axis, If the current carried by the solenoid changes steadily from 2.0 A to 4.0 A in 0.1 s, what is the inducced emf in the loop while the current is changing?
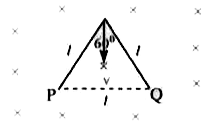
View SolutionA wire of length 2l is bent at mid point so that the angle between two halves is `60^@` . If it moves as shown with a velocity v in a magnetic field B find the induced emf.
View SolutionA conductor of length 0.1m is moving with a velocity of 4m/s in a uniform magnetic field of 2T as shown in the figure. Find the emf induced ?
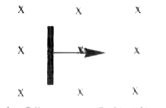
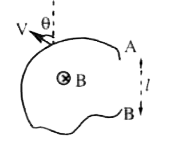
View SolutionFigure shows an irregular shaped wire AB moving with velocity v, as shown. Find the emf induced in the wire
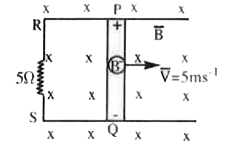
View SolutionFigure shows a conducting rod PQ in contact with metal rails RP and SQ, which are 0.25m apart in a uniform magnetic field of flux density 0.4T acting perpendicular to the plane of the paper. Ends R and S are connected through a `5Omega` resistance. What is the emf when the rod moves to the right with a velocity of `5ms^(-1)` ? What is the magnitude and direction of the current through the `5Omega` resistance? If the rod PQ moves to the left with the same speed, what will be the new current and its direction?
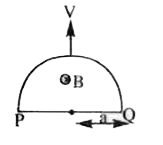
View SolutionFind the emf across the points P and Q which are diametrically opposite points of a semicircular closed loop in a magnetic of each branch.
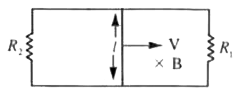
View SolutionA loop ABCD containing two resistors as shown in figure is placed in a uniform magnetic field B directed outward to the plane of page. A sliding conductor EF of length l and of negligible resistance moves to the right with a uniform velocity v as shown in Fig. Determine the current in each branch.
View SolutionA conducting rod PQ of length L = 1.0m is moving with a uniform speed v= 2.0 m/s in a uniform magnetic field B = 4.0 T directed into the paper. A capacitor of capacity `C = 10 mu F` is connected as shown in the figure. Then what are the charges on the plates A and B of the capacitor.
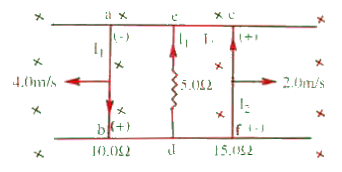
View SolutionTwo parallel rails with negligible resistance are 10.0cm apart. They are connected by a 5.0 `Omega` resistor. The circuit also contains two metal rods having resistances of 10.0 `Omega` and 15.0 `Omega` along the rails. The rods are pulled away from the resistor at constant speeds 4.00 `m//s` and 2.00 `m//s` respectively. A uniform magnetic field of magnitude 0.01 T is applied perpendicular to the plane of the rails. Determine the current in the 5.0 `Omega` resistor:
View SolutionA rectangular loop with a slide wire of length l is kept in a uniform magnetic field as shown in the figure. The resistance of slider is R. Neglecting self inductance of the loop find the current in the connector during its motion with a velocity v.
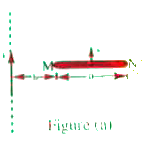
View SolutionA conducting rod MN moves with a speed v parallel to a long straight wire which carries a constant current i, as shown in Fig. The length of the rod is normal to the wire. Find the emf induced in the total length of the rod. State which end will be at a lower potential.
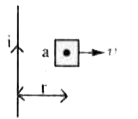
View SolutionA square loop of side a is placed in the same plane as a long straight wire carrying a current i. The centre of the loop is at a distance r from the wire where r > > a. The loop is moved away from the wire with a constant velocity v. The induced e.m.f. in the loop is
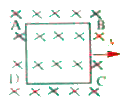
View SolutionA metallic square loop ABCD is moving in its own plane with velocity v in a uniform magnetic field perpendicular to its plane as shown in the figure, Find
a) in which sides of the loop electric field is induced.
b) Net emf induced in the loop.
c) If one side .BC. is outside the field with remaining loop in the field and is being pulled on D with a constant velocity then induced current in the loop.
View Solution
Two conducting rings of radii r and 2r move in opposite directions with velocities 2v and v respectively on a conducting surface S. There is a uniform magnetic field of magnitude B perpendicnlar to the plane of the rings. The potential difference between the highest points of the two rings is
View SolutionA copper rod of length 2m is rotated with a speed of 10 rps, in a uniform magnetic field of T tesla about a pivot at one end. The magnetic field is perperndicular to the plane of rotation. Find the emf induced across its ends
View SolutionA rod of length 10 cm is made up of conducting and non-conducting material (shaded part is nonconducting), the rod is rotated with constant magnetic field of 10 `rad//s` about point O, in a constant magnetic field of 2T as shown in the figure. Fing induced emf between the points A and B?

View SolutionA wheel with 10 metallic spokes, each 0.50 m long, is rotated with a speed of 120 `rev // "minute"` in a plane normal to the earth.s magnetic field at the place. If the magnitude of the field is 0.40 gauss, what is the induced emf between the axle and the rim of the wheel?

View SolutionA metal rod of resistance 20 `Omega` is fixed along a diameter of a conducting ring of radius 0.1m and lies on x-y plane. There is a magnetic field `B =(50T)hatk`. The ring rotates with an angular velocity `omega=20 rad //s` about its axis. An external resistance of 10 `Omega` is connected across the centre of the ring and rim. The current through external resistance is
View SolutionA copper disc of radius Im is rotated about its natural axis with an angular velocity 2 rad/sec in a uniform magnetic field of 5 tesla with its plane perpendicular to the field. Find the emf induced between the centre of the disc and its rim.
View SolutionA pair of parallel horizontal conducting rails of negligible resistance, shorted at one end is fixed on a table. The distance between the rails is L. A conducting mussless rod of resistance R can slide on the rails frictionlessly. The rod is tied to a massless string which passes over a pulley fixed to the edge of the table. A mass m, tied to the other end of the string, hangs vertically. A constant magnetic field B exists perpendicular to the table. If the system is released from rest, calculate :
i) the terminal velocity achieved by the rod.
ii) the acceleration of the mass at the instant when the velocity of the rod, is half the terminal velocity.
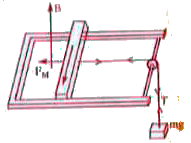
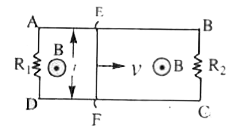
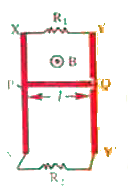
View SolutionTwo parallel vertical metallic bars XX.and YY., of negligible resistance and separated by a length .l., are as shown in Fig. The ends of the bars are joined by resistance `R_(1)` and `R_(2)`. A uniform magnetic field of induction B exists in space normal to the plane of the bars. A horizontal metallic rod PQ of mass m starts falling vertically, making contact with the bars. It is observed that in the steady state the powers dissipated in the resistance `R_(1)` and `R_(2)` are `P_(1)` and `P_(2)` respectively. Find an expression for `R_(1), R_(2)` and the terminal velocity attained by the rod PQ
View SolutionA short - circuited coil is placed in a time varying magnetic field. Electrical power is dissipated due to the current induced in the coil. If the number of turns were to be quadrupled and the radius of the wire is to be halved, then find the electrical power dissipated.
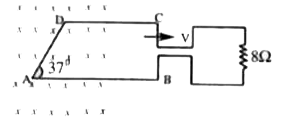
View SolutionThe loop ABCD is moving with velocity .v. towarris right. The magnetic field is 4 T. The loop is connected to a resistance of 8 ohm. If steady current of 2 A flows in the loop then value of v if loop has a resistance of 4 ohm, is:
(Given AB=30 cm, AD=30 cm)

View SolutionA square loop of side 12 cm with its sides parallel to X and velocity of 8 cm s in the positive x-direction in an environment containing a magnetic field in the positive z-direction. The field is neither uniform in space nor constant in time. It has a gradient of 10 T cm along the negative x-direction (that is it increases by 103 T cm- as one moves in the negative x-direction), and it is decreasing in time at the rate of 103 Ts. Determine the direction and magnitude of the induced current in axes is moved with a the loop if its resistance is 4.50 m2. Sol. Given, side of loop a = 12 cm . Area of loop (A) = a = (12) = 144 cm = 144 x 10 m? (. Area of square = (side))
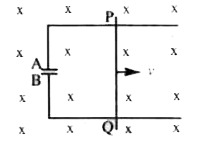
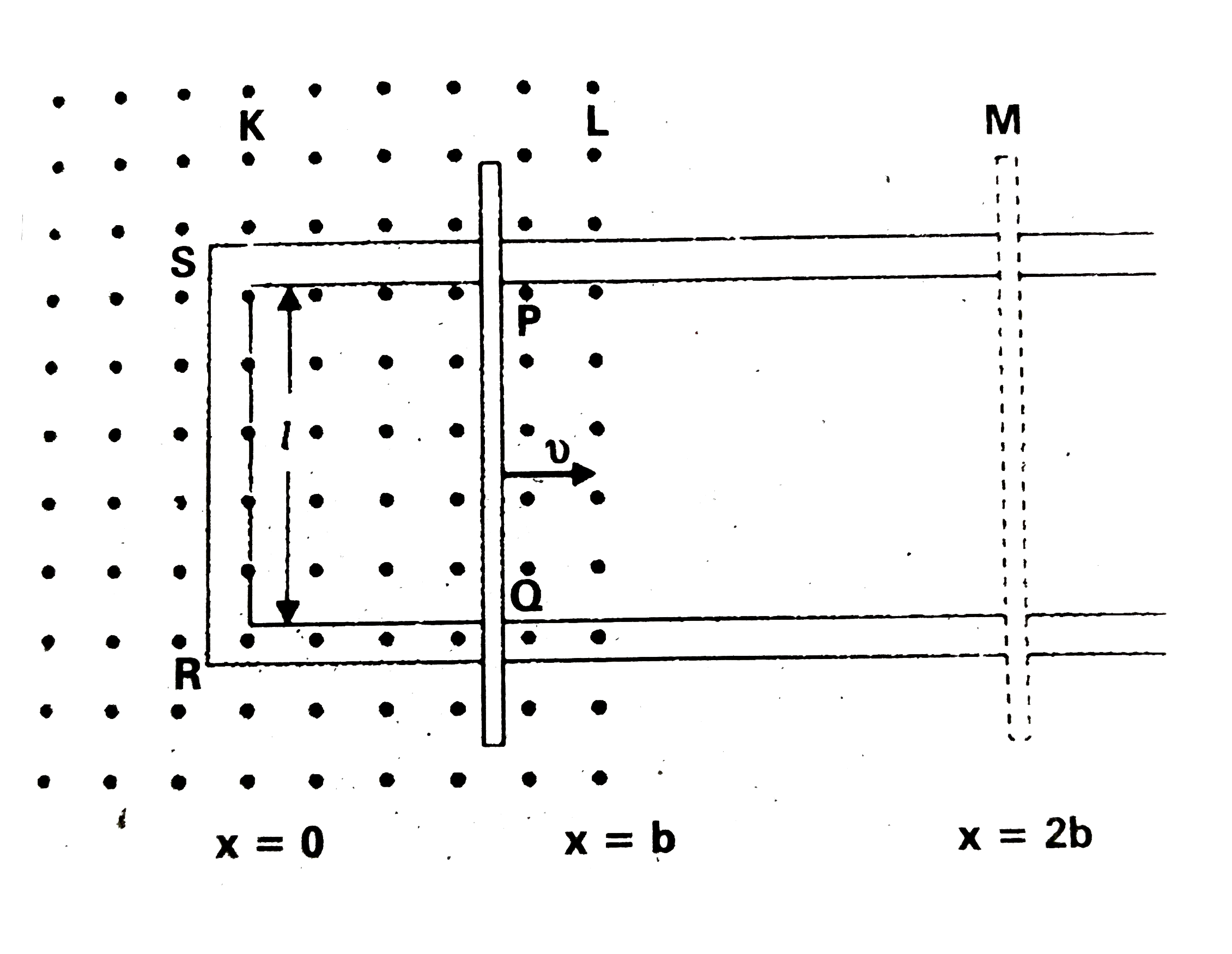
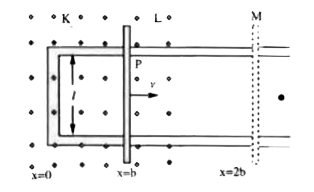
View SolutionRefer to fig. The arm PQ of the rectangular conductor is moved from x=0 outwards. The uniform magnetic field is perpendicular to the plane and extends from x=0 to x=b and is zero for `x gt b`. Only the arm PQ possesses substantial resistance r. Consider the situation when the arm PQ is pulled outwards from x=0 to x=2b, and is then moved back x=0 with constant speed `upsilon`. Obtain expressions for the flux the induced emf, the force necessary to pull the arm and the power dissipated as Joule heat. Sketch the variation of these quantities with distance.
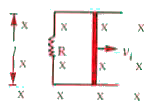
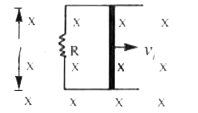
View SolutionA bar of mass mand length I moves on two frictionless parallel rails in the presence of a uniform magnetic field directed into the plane of the paper. The bar is given an initial velocity `v_(i)` to the right and released. Find the velocity of bar, induced emfacross the bar und the current in the circuit as a function of time.
View SolutionTwo concentric circular coil,s one of small radius `r_(1)` and the other of large radius `r_(2)`, such that `r_(1) lt lt r_(2)`, are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement.
View SolutionA small square loop of wire of side 'I' is placed inside a large square loop of side L (L > I). If the loops are coplanar and their centres coincide, the mutual inducation of the system is directly proportional to
View SolutionThe self-inductance of a coil having 200 turns is 10 milli henry. Calculate the magnetic flux through the cross-section of the coil corresponding to current of 4 milliampere. Also determine the total flux linked with each turn.
View SolutionAn inductor of 5 H inductance carries a steady current of 2A. How can a 50 V self-induced emf be made to appear in the inductor ?
View SolutionTwo different coils have self- inductances `L_(1) = 16` mH and `L_(2)= 12`mH. At a certain instant, the current in the two coils is increasing at the same rate and power supplied to the two coils is the same. Find the ratio of i) induced voltage ii) current it) energy stored in the two coils at that instant.
View SolutionThe network shown is a part of the closed circuit which the current is changing. At an instant, current in it is 5A. Potential difference between the points A and B if the current is

1) increasing at 1 `A//sec` 2) decreasing at 1`A//sec`
View SolutionA coil of inductance 0.2 henry is connected to 600 volt battery. At what rate, will the current in the coil grow when circuit is completed?
View SolutionCalculate the mutual inductance between two coils when a current of 2A changes to 6A in 2 seconds and induces an emf of 20 mV in the secondary coil.
View SolutionA solenoid is of length 50 cm and has a radius of 2cm. It has 500 turns. Around its central section a coil of 50 turns is wound. Calculate the mutual inductance of the system.
View SolutionAn air-cored solenoid is of length 0.3 m, area of cross section `1.2 xx 10^(-3) m^(2)` and has 2500 turns. A roand its central section, a coil of 350 turns is wound. The solenoid and the coil are electrically insulated from each other. Calculate the enfinduced in the coil if the initial current of 3 A in the solenoid is reversed in 0.25s.
View SolutionIf the coefficient of mutual induction of the primary and secondary coils of an induction coil is 6 H and a current of 5A is cut off in `1//5000` second, calculate the conf. induced in the secondary coil.
View Solution(a) A toroidal solenoid with an ain core has an average radlines of 0.15m, area of cross section `12 xx 10^(-4) m^(2)` and 1200 turns. Obtain the self inductance of the foroid. Ignore field variation across the cross section of the foroid. (b) A second coil of 300 turns is wound closely on the toroid above. If the current in the primary coil is increased from zero to 2.0 A in 0.05 s, obruin the induced emſ in the secondary coil.
View SolutionA solenoidal coil has 50 turns per centimetre along its length and a cross-sectional area of `4xx10^(-4)m^(2)`. 200 turns of another wire is wound round the first solenoid co-axially. The two coils are electrically insulated from each other. Calculate the mutual inductance between the two coils.
View SolutionA solenoid of length 50cm with 20 turns per centimetre and area of cross-section 40cm? completely surrounds another coaxial solenoid of the same length, area of cross-section `25cm^(2)` with 25 turns per centimetre. Calculate the mutual inductance of the system.
View SolutionChaitanya pedals a stationary bicycle at one revolution per second. The pedals are attached to 100 turns coil of area `0.1m^(2)` and placed in a uniform magnetic field of 0.1 T. What is the maximum voltage generated in the coil ?
View SolutionA coil of 800 turns and `50 cm^(2)` area makes 10 rps about an axis in its own plane in a magnetic field of 100 gauss perpendicular to this axis. What is the instantaneous induced emf in the coil?
View SolutionKamla peddles a stationary bicyle, the pedals of the bicycle are attached to a 100 turns coil of area `0.10m^(2)`. The coil rotates at half a revolution per second and it is placed in a uniform magnetic field of 0.01T perpendicular to the axis of rotation of the coil. What is the maximum voltage generated in the coil.
View SolutionThe magnetic field at all points within the cylindrical region whose cross-section is indicated in the accompanying figure starts increasing at a constant rate .`alpha`.. Find the magnitude of electric field as a function of r, the distance from the geometric centre of the region.

View SolutionA magnetic field directed into the page changes with time according to the expression `B = (0.03t^(2) +1.4)T`, where t is in seconds. The field has a circular cross-section of radius R = 2.5cm. What is the magnitude and direction of electric field at P, when t=3.0s and r=0.02 m.
View SolutionA wire is bent in the form of a square of side la in a varying magnetic field `B= prop B_(0)t hatk`. If the resistance per unit length is `lambda`. then find the following:
(i) The direction of induced current
(ii) The current in the loop
(iii) Potential difference between P and Q
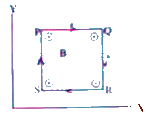
View SolutionShown in the figure is a circular loop of radius r connected to a resistance R. A variable magnetic field of K induction `B = e^(-t)` is established inside the coil. If the key(k) is closed, find the electric power developed ?
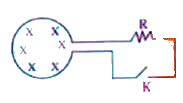
View SolutionAn inductor of 3H is connected to a battery of emf 6V through a resistance of 100 `Omega`. Calculate the time constant. What will be the maximum value of current in the circuit ?
View SolutionA cell of 1.5V is connected across an inductor of 2mH in series with a 2 `Omega` resistor What is the rate of growth of current immediately after the cell is switched on.
View SolutionA coil having resistance 15 and inductance 10 H is connected across a 90 Volt supply. Determine the value of current after 2sec . What is the energy stored in the magnetic field at that instant
View SolutionAn inductor of 10mH is connected to a 18V battery through a resistor of 10k`Omega` and a switch After a long time, when the maximum current is set up in the circuit, the current is switched off. Calculate the cur- rent in the circuit after 2 `mu`s.
View SolutionCalculate the back e.m.f of a 10H, 200 `Omega` coil 100 ms after a 100Vdc supply is connected to it.
View SolutionThe time constant of a certain inductive coil was found to be 2.5 ms. With a resistance of 80`Omega` added in series, a new time constant of 0.5 ms was obtained. Find the inductance and resistance of the coil.
View SolutionWhen a coil joined to a cell, the current through the coil grows with a time constant `tau`. After what time, the current will reach 10% of its steady- state value?
View SolutionAt t=0, an inductor of zero resistance is joined to a cell of emf `epsilon` through a resistance. The current increases with a time constant `tau`. After what time will the potential difference across the coil be equal to that across the resistance ?
View SolutionA coil of resistance `20 Omega` and inductance 0.5 henry is switched to dc 200 volt supply. Calculate the rate of increase of current :
a) at the instant of closing the switch and
b) after one time constant.
c) Find the steady state current in the circuit.
View SolutionIn the circuit shown in figure switch S is closed at time t = 0. Find the current through different wires and charge stored on the capacitor at any time t.

View SolutionA parallel - plate capacitor, filled with a dielectric of dielectric constant k, is charged to a potential `V_(0)`. It is now disconnected from the cell and the slab is removed. If it now discharges, with time constant `tau`, through a resistance, then find time after which the potential difference across it will be `V_(0)`?
View SolutionFind the values of `i_(1)` and `i_(2)`
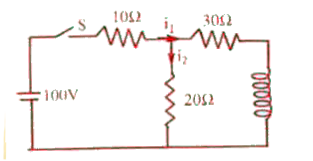
i) immediately after the switch S is closed.
ii) long time later, with S closed
ii) immediately after S is reopende
View SolutionSuppose the emf of the battery in the circuit shown varies with time t, so the curent is given by i(t) = 3 + 5t, where i is in amperes & t is in seconds. Take `R=4 Omega` L = 6H then find an expression for the battery emf as function of times.
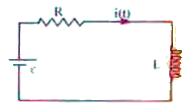
View Solution`4muF` capacitor and a resistance 2.5M `Omega` are in series with 12V battery, Find the time after which the potential difference across the capacitor is 3 times the potential difference across the resistor.
[Given In ( 2 ) = 0.693]
View SolutionA coil of inductance 8.4 mH and resistance 6 `Omega` are connected to a 12 V battery. At what time the current in the coil will be 1.0 A ?
View SolutionIn a circuit R inductance L and capacitance C are connected as shown in figure and `A_(1)` and `A_(2)` are ammeters. When key k is pressed to complete the circuit , then just after closing key k, the readings of `A_(1)` and `A_(2)` will be :

View SolutionA rectangular loop of area 0.06 m2 is placed in a magnetic field of 0.3T with its plane (i) normal to the field (ii) inclined `30^(@)` to the field (iii) parallel to the field. Find the flux linked with the coil in each case.
View SolutionAt a certain location in the northern hemisphere, the earth.s magnetic field has a magnitude of `42 muT` and points downwards at `53^@` to the vertical. Calculate the flux through a horizontal surface of area `2.5 m^2. [sin 53^@ = 0.8]`

View SolutionThe magnetic flux through a coil perpendicular to its plane is varying according to the relation `phi_B = (5t^3 +4t^2 +2t-5)` weber. Calculate the induced current through the coil at t = 2 second. The resistance of the coil is `5Omega`
View SolutionA circular coil of 500 turns of wire has an enclosed area of `0.1m^2 ` per turn. It is kept perpendicular to a magnetic field of induction 0.27 and rotated by `180^@` about a diameter perpendicular to the field in 0.1 s. How much charge will pass when the coil is connected to a galvanometer with a combined resistance of `50Omega`
View SolutionSome magnetic flux is changed from a coil of resistance `10Omega` . As a result an induced current is developed in it, which varies with time as shown in figure. What is the magnitude of change in flux through the coil ?
View SolutionA tong solenoid with 15 turns per em has a small loop of area `2.0 cm^(2)` placed inside the solenoid normal to its axis, If the current carried by the solenoid changes steadily from 2.0 A to 4.0 A in 0.1 s, what is the inducced emf in the loop while the current is changing?
View SolutionA wire of length 2l is bent at mid point so that the angle between two halves is `60^@` . If it moves as shown with a velocity v in a magnetic field B find the induced emf.

View SolutionA conductor of length 0.1m is moving with a velocity of 4m/s in a uniform magnetic field of 2T as shown in the figure. Find the emf induced ?
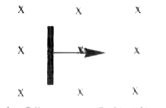
View SolutionFigure shows an irregular shaped wire AB moving with velocity v, as shown. Find the emf induced in the wire

View SolutionFind the emf across the points P and Q which are diametrically opposite points of a semicircular closed loop in a magnetic of each branch.

View SolutionFigure shows a conducting rod PQ in contact with metal rails RP and SQ, which are 0.25m apart in a uniform magnetic field of flux density 0.4T acting perpendicular to the plane of the paper. Ends R and S are connected through a `5Omega` resistance. What is the emf when the rod moves to the right with a velocity of `5ms^(-1)` ? What is the magnitude and direction of the current through the `5Omega` resistance? If the rod PQ moves to the left with the same speed, what will be the new current and its direction?

View SolutionA loop ABCD containing two resistors as shown in figure is placed in a uniform magnetic field B directed outward to the plane of page. A sliding conductor EF of length l and of negligible resistance moves to the right with a uniform velocity v as shown in Fig. Determine the current in each branch.

View SolutionA rectangular loop with a slide wire of length l is kept in a uniform magnetic field as shown in the figure. The resistance of slider is R. Neglecting self inductance of the loop find the current in the connector during its motion with a velocity v.

View SolutionA conducting rod PQ of length L = 1.0m is moving with a uniform speed v= 2.0 m/s in a uniform magnetic field B = 4.0 T directed into the paper. A capacitor of capacity `C = 10 mu F` is connected as shown in the figure. Then what are the charges on the plates A and B of the capacitor.

View SolutionTwo parallel rails with negligible resistance are 10.0cm apart. They are connected by a 5.0`Omega` resistor. The circuit also contains two metal rods having resistances of 10.0`Omega ` and 15.0`Omega` along the rails. The rods are pulled away from the resistor at constant speeds 4.00 m/s and 2.00 m/s respectively. A uniform magnetic field of magnitude 0.01 T is applied perpendicular to the plane of the rails. Determine the current in the 5.0`Omega` resistor.
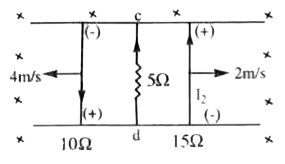
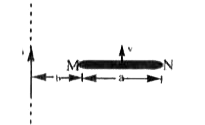
View SolutionA conducting rod MN moves with a speed v parallel to a long straight wire which carries a constant current i, as shown in Fig. The length of the rod is normal to the wire. Find the emf induced in the total length of the rod. State which end will be at a lower potential.
View SolutionA square loop of side a is placed in the same plane as a long straight wire carrying a current i. The centre of the loop is at a distance r from the wire where r > > a. The loop is moved away from the wire with a constant velocity v. The induced e.m.f. in the loop is

View Solution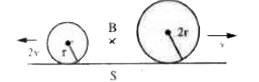
Two conducting rings of radii r and 2r move in opposite directions with velocities 2v and v respectively on a conducting surface S. There is a uniform magnetic field of magnitude B perpendicular to the plane of the rings. The potential difference between the highest points of the two rings is
View SolutionA metallic square loop ABCD is moving in its own plane with velocity v in a uniform magnetic field perpendicular to its plane as shown in the figure. Find a) In which sides of the loop electric field is induced. b) Net emf induced in the loop. c) If one side .BC. is outside the field with remaining loop in the field and is being pulled out with a constant velocity then induced current in the loop.
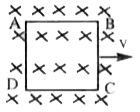
View SolutionA copper rod of length 2m is rotated with a speed of 10 rps, in a uniform magnetic field of 1 tesla about a pivot at one end. The magnetic field is perpendicular to the plane of rotation. Find the emf induced across its ends
View SolutionA rod of length 10 cm is made up of conducting and non-conducting material (shaded part id non conducting), the rod is rotated with constant magnetic field of 10 rad/s about point o, in a constant magnetic field of 2T as shown in the figure. Find induced emf between the points A and B?
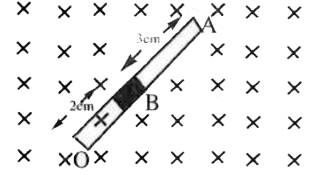
View SolutionA wheel with 10 metallic spokes, each 0.50 m long, is rotated with a speed of 120 rev/minute in a plane normal to the earth.s magnetic field at the place. If the magnitude of the field is 0.40 gauss, what is the induced emf between the axle and the rim of the wheel?

View SolutionA metal rod of resistance 20`Omega` is fixed along a diameter of a conducting ring of radius 0.1m and lies on x-y plane. There is a magnetic field `vecB = (50T)hatk` . The ring rotates with an angular velocity `omega ` = 20rad /s about its axis. An external resistance of 10`Omega ` is connected across the centre of the ring and rim. The current through external resistance is
View SolutionA copper disc of radius 1m is rotated about its natural axis with an angular velocity 2 rad /sec in a uniform magnetic field of 5 tesla with its plane perpendicular to the field. Find the emf induced between the centre of the disc and its rim.
View SolutionA short-circuited coil is placed in a time varying magnetic field. Electrical power is dissipated due to the current induced in the coil. If the number of turns were to be quadrupled and the radius of the wire is to be halved, then find the electrical power dissipated
View SolutionA pair of parallel horizontal conducting rails of negligible resistance, shorted at one end is fixed on a table. The distance between the rails is L. A conducting massless rod of resistance R can slide on the rails frictionlessly. The rod is tied to a massless string which passes over a pulley fixed to the edge of the table. A mass m, tied to the other end of the string, hangs vertically. A constant magnetic field B exists perpendicular to the table. If the system is released from rest, calculate :
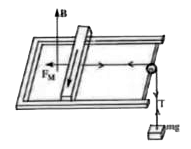
i) the terminal velocity achieved by the rod. ii) the acceleration of the mass at the instant when the velocity of the rod, is half the terminal velocity.
View SolutionTwo parallel vertical metallic bars XX. and YY., of negligible resistance and separated by a length .l., are as shown in Fig. The ends of the bars are joined by resistance `R_1` and `R_2` A uniform magnetic field of induction B exists in space normal to the plane of the bars. A horizontal metallic rod PQ of mass m starts falling vertically, making contact with the bars. It is observed that in the steady state the powers dissipated in the resistance `R_1` and `R_2` are `P_1` and `P_2` respectively. Find an expression for `R_1, R_2` and the terminal velocity attained by the rod PQ.
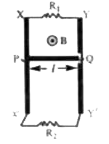
View SolutionThe loop ABCD is moving with velocity .v. towards right. The magnetic field is 4 T. The loop is connected to a resistance of 8 ohm. If steady current of 2 A flows in the loop then value of u if loop has a resistance of 4 ohm, is : (Given AB=30 cm, AD=30 cm)
View SolutionA square loop of side 12 cm with its sides parallel to x and y-axes is moved with a velocity 8 cm/s along positive x-direction in an environment containing magnetic field along +ve z-direction. The field has a gradient of `10^(-3)` tesla/em along -ve x-direction (increasing along -ve x-axis) and also decreases with time at the rate of `10^(-3)` tesla/s. The emf induced in the loop is
View SolutionA bar of mass m and length I moves on two frictionless parallel rails in the presence of a uniform magnetic field directed into the plane of the paper. The bar is given an initial velocity v to the right and released. Find the velocity of bar, induced emf across the bar and the current in the circuit as a function of time.
View SolutionThe arm PQ of the rectangular conductor is moved from x=0, outwards in the uniform magnetic field which extends from r=0 to x=b and is zero for x > b as shown. Only the arm PQ possesses substantial resistance r. Consider the situation when the arm PQ is pulled outwards from x = 0 to x = 2b, and is then moved back to x = 0 with constant speed v. Obtain expressions for the flux, the induced emf, the force necessary to pull the arm and the power dissipated as Joule heat. Sketch the variation of these quantities with distance.
View SolutionTwo concentric circular coils, one of small radius r, and the other of large radius `r_2`, such that `r_1 lt lt r_2` , are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement.
View Solution
PROBLEM questions and complete solutions for chapter ELECTROMAGNETIC INDUCTION of JEE (MAIN AND ADVANCED) PHYSICS of Class 12
All Exercises from AAKASH SERIES Class 12 PHYSICS ELECTROMAGNETIC INDUCTION
- Additional Exercise
- Example
- Exercise (Short Answer Questions)
- Exercise (Very Short Answer Questions)
- EXERCISE - I (ASSERTION AND REASON)
- EXERCISE - I (MAGNETIC FLUX, FARADAY.S LAW, LENZ.S LAW, AC GENERATOR)
- EXERCISE - I (SELF AND MUTUAL INDUCTION)
- EXERCISE - II (DC CIRCUITS)
- EXERCISE - II (MAGNETIC FLUX, FARADAY.S LAW, LENZ.S LAW , AC GENERATOR)
- EXERCISE - II (MOTIONAL EMF)
- EXERCISE - II (SELF INDUCTANCE AND MUTUAL INDUCTANCE)
- EXERCISE-IA
- EXERCISE-IB
- EXERCISE-II
- EXERCISE-III
- PRACTICE EXERCISE (MAGNETIC FLUX, FARADAY.S LAW, LENZ.S LAW , AC GENERATOR)
- PRACTICE EXERCISE (MOTIONAL EMF)
- PRACTICE EXERCISE (SELF INDUCTANCE AND MUTUAL INDUCTANCE)
- PROBLEM
- Problems (Level-I)
- Problems (Level-II)