Complete Solutions to Example of chapter ELECTROMAGNETIC INDUCTION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTROMAGNETIC INDUCTION |
| AAKASH SERIES | Example |
| Number Of Questions | 39 |
| Academic Year | 2023-24 |
A rectangular loop of area `0.06 m2` is placed in a magnetic field of 0.3T with its plane (i) normal to the field (ii) inclined `30^(@)` to the field (iii) parallel to the field. Find the flux linked with the coil in each case.
View SolutionAt a certain location in the northern hemisphere, the earth's magnetic field has a magnitude of `42 mu T` and points downwards at `53^(@)` to the vertical. Calculate the flux through a horizontal surface of area `2.5 m^(2), [sin 53^(@)= 0.8]`

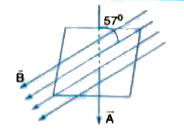
View SolutionAt a certain location in the northern hemisphere, the earth's magnetic field has a magnitude of `42mu T` and points downwards at `57^(@)` to the vertical. Calculate the flux through a horizontal surface of area `2.5 m^(2)`.
View SolutionThe flux of magnetic field through a closed conducting loop changes with time according to the equation `phi= 0.2t^(2) + 0.4t + 0.6`. Find the induced e.m.f at t= 2s.
View SolutionThe magnetic flux through a coil perpendicular to its plane is varying according to the relation `phi_(B)= (5t^(3) + 4t^(2) + 2t -5)` weber. Calculate the induced current through the coil at 1= 2 second. The resistance of the coil is `5 Omega`
View SolutionA circular of 500 turns of wire has anclosed area of `0.1m^(2)` per turn. It is kept perpendicular to a magnetic field of induction 0.2T and rotated by `180^(@)` about a diameter perpendicular to the field in 0.1s. How much charge will pass when the coil is connected to a galvanometer with a combined resistance of `50 Omega`.
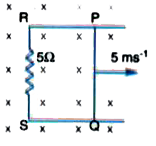
View SolutionFigure shows a conducting rod PQ in contract with metal rails RP and SQ, which are 0.25m apart in a uniform magnetic field of flux density 0.4T acting perpendicular to the plane of the paper. Ends R and S are connected through a `5Omega` resistance. What is the emf when the rod moves to the right with a velocity of `5ms^(-1)` ? What is the magnitude and direction of the current through the `5Omega` resistance ? If the rod PQ move to the left with the same speed, what will be the new current and its direction
View SolutionA wire of length 2l is bent at mid point so that the angle between the two halves is `60^(@)`. If it moves as shown with a velocity v in a magnetic field B, find the induced emf.

View SolutionA conductor of length 0.1m is moving with a velocity of 4m/s in a uniform magnetic field of 2T as shown in the figure. Find the emf induced?
View SolutionFind the emf induced across the ends of the conductor shown in the figure

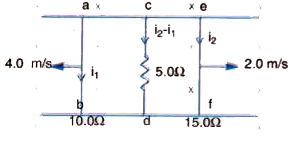
View SolutionTwo parallel rails with negligible resistance are 10.0cm apart. They are connected by a `5.0 Omega` resistor. The circuit also contains two metal rods having resistances of `10.0 Omega and 15.0 Omega` across the rails. The rods are pulled away from the resistor at constant speeds 4.00m/s and 2.00m/s respectively. A uniform magnetic field of magnitude 0.01T is applied perpendicular to the plane of the rails. Determine the current in the `5.0 Omega` resistor.
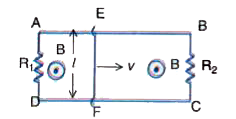
View SolutionA loop ABCD containing two resistors is placed in a uniform magnetic field B directed out of the plane of the page. A sliding conductor EF of length l and of negligible resistance moves to the right with a uniform velocity v as shown in the figure. Determine the current in each branch.
View SolutionA conducting rod MN moves with a speed v parallel to a long straight wire which carries a constant current i, as shown in Fig. The length of the rod is normal to the wire, Find the emf induced in the total length of the rod state which end will be at a lower potential,
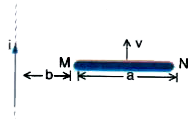
View SolutionTwo parallel vertical metallic bars XX' and YY', of negligible resistances are separated by a length T, as shown in Fig. The ends of the bars are joined by resistance `R_(1) and R_(2)`. A uniform magnetic field of induction B exists in space normal to the plane of the bars. A horizontal metallic rod PQ of mass m starts falling vertically, making contact with the bars. It is observed that in the steady state the power dissipated in the resistances `R_(1) and R_(2) "are " P_(1) and P_(2)` respectively. FInd an expression for `R_(1), R_(2)` and the terminal velocity attained by the rod PQ.

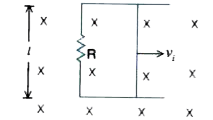
View SolutionA bar of mass m and length l moves on two frictionless parallel rails in the presence of a uniform magnetic field directed into the plane of the paper. The bar is given an initial velocity `v_(i)` to the right and released. Find the velocity of bar, induced emf across the bar and the current in the circuit as functions of time
View SolutionA copper rod of length 2m is rotated with a speed of 10 rps in a uniform magnetic field of 1 tesla about a pivot at one end. The magnetic field is perpendicular to the plane of rotation. Find the emf induced across its ends.
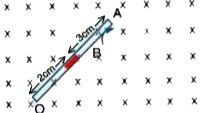
View SolutionA rod of length 10cm is made up of conducting and non-conducting material (shaded part is non-conducting). The rod is rotated with constant angular velocity 10 rad/s about point O, in a constant magnetic field of 2T as shown in the figure. Find induced emf between the points A and B ?
View SolutionA copper disc of radius 1m is rotated about its natural axis with an angular velocity 2 rad/sec in a uniform magnetic field of 5 tesla with its plane perpendicular to the field. Find the emf induced between the centr of the disc and its rim.
View SolutionA wheel with 10 metallic spokes, each 0.50 m long, is rotated with a speed of 120 rev/minute in a plane normal to the earth's magnetic field at the place. If the magnitude of the field is 0.40 gauss, what is the induced emf between the axle and the rim of the wheel?
View SolutionChaitanya pedals a stationary bicycle at one revolution per second. The pedals are attached to 100 turns coil of area `0.1m^(2)` and placed in a uniform magnetic field of 0.1T. What is the maximum voltage generated in the coil?
View SolutionA coil of 800 turns and `50cm^(2)` are makes 10 rps about an axis in its own plane in a magnetic field of 10gauss perpendicular to this axis. What is the instantaneous induced emf in the coil?
View SolutionA magnetic field directed into the page changes with time according to the expression `B = (0.03t^(2) + 1.4)T`, where t is in seconds. The field has a circular cross-section of radius R= 2.5cm. What is the magnitude and direction of electric field at P, when t= 3.0s and r= 0.02m
View SolutionThe magnetic field at all points within the cylindrical region whose cross-section is indicated in the accompanying figure starts increasing at a constant rate `'alpha'`. Find the magnitude of electric field as a function of r, the distance from the geometric centre of the region.

View SolutionA wire is bent in the form of a square of side a in a varying magnetic field `vec(B)= prop B_(0) t hat(k)`. If the resistance per unit length is `lamda`, then find the following
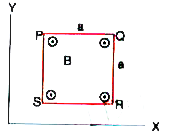
(i) The direction of induced current
(ii) The current in the loop
(iii) Potential difference between P and Q
View SolutionShown in the figure is a circular loop of radius r connected to a resistance R. A variable magnetic field of induction `B= e^(-t)` is established inside the coil. If the key (K) is closed, find the electric power developed

View SolutionThe figure shows two circular rings of radii a and b `(a gt b)` made of a wire whose resistance is `lamda` per unit length

All the three arrangemetns are placed in a uniform time varying magnetic field `(dB)/(dt)= k`, perpendicular to the plane of the loops. Determine the current induced in each case.
View SolutionThe self-inductance of a coil having 200turns is 10 millihenry. Calculate the magnetic flux through the cross-section of the coil corresponding to current of 4 milliampere. Also determine the total flux linked with the coil.
View SolutionA coil of inductance 0.2 henry is connected to 600volt battery. At what rate will the current in the coil grow when circuit is completed?
View SolutionAn inductor of 5H inductance carries a steady current of 2A. How can a 50V self-induced emf to made to appear in the inductor?
View SolutionTwo different coils have self-inductances `l_(1)= 16 mH and L_(2)= 12mH`. At a certain instant, the current in the two coils is increasing at the same rate and power supplied to the two coils is the same. Find the ratio of
(i) induced voltage (ii) current (iii) energy stored in the two coils at that instant
View SolutionCalculate the mutual inductance between two coils when a current of 2A changes to 6A in 2 seconds and induces an emf of 20mV in the secondary coil.
View SolutionIf the coefficient of mutual induction of the primary and secondary coils of an induction coil is 6H and a current of 5A is cut off in 1/5000 second, calculate the emf induced in the secondary coil.
View SolutionA solenoid is of length 50cm and has a radius of 2cm. It has 500 turns. Around its central section of coil of 50 turns is wound. Calculate the mutual inductance of the system.
View SolutionAn air-cored solenoid is of length 0.3m, area of cross section `1.2 xx 10^(-3)m^(2)` and has 2500 turns. Around its central section, a coil of 350 turns is wound. The solenoid and the coil are electrically insulated from each other. Calculate the emf induced in the coil if the initial current of 3A in the solenoid is reversed in 0.25s.
View SolutionA solenoid of length 50cm with 20turns per centimetre and area of cross-section `40cm^(2)` completely surrounds another co-axisal solenoid of the same length, area of cross-section `25cm^(2)` with 25 turns per centimetre. Calculate the mutual inductance of the system.
View SolutionA solenoidal coil has 50 turns per centimetre along its length and a cross-sectional area of `4 xx 10^(-4) m^(2)`. 200 turns of another wire is wound round the first solenoid co-axially. The two coils are electrically insulated from each other. Calculate the mutual inductance between the two coils.
View SolutionTwo circular coils, one of smaller radius `r_(1)` and the other of very large radius `r_(2)` are placed co-axially with centres coinciding. Obtain the mutal inductance of the arrangement.
View Solution(a) A toroidal solenoid with an air core has an average radius of 0.15m, area of cross section `12 xx 10^(-4) m^(2)` and 1200 turns. Obtain the self inductance of the toroid. Ignore field variation across the cross section of the toroid. (b) A second coil of 300 turns is wound closely on the toroid above. If the current in the primary coil is increased from zero to 2.0 A in 0.05s, obtain the induced emf in the secondary coil.
View SolutionA circular loop of radius 0.3cm lies parallel to a much bigger circular loop of radius 20cm. The centre of the small loop is on the axis of the bigger loop. The distance between their centres is 15cm.
(a) What is the flux linking the bigger loop if a current of 2.0 A flows through the smaller loop ?
(b) Obtain the mutual inductance of the two loops.
View Solution
Example questions and complete solutions for chapter ELECTROMAGNETIC INDUCTION of JEE (MAIN AND ADVANCED) PHYSICS of Class 12
All Exercises from AAKASH SERIES Class 12 PHYSICS ELECTROMAGNETIC INDUCTION
- Additional Exercise
- Example
- Exercise (Short Answer Questions)
- Exercise (Very Short Answer Questions)
- EXERCISE - I (ASSERTION AND REASON)
- EXERCISE - I (MAGNETIC FLUX, FARADAY.S LAW, LENZ.S LAW, AC GENERATOR)
- EXERCISE - I (SELF AND MUTUAL INDUCTION)
- EXERCISE - II (DC CIRCUITS)
- EXERCISE - II (MAGNETIC FLUX, FARADAY.S LAW, LENZ.S LAW , AC GENERATOR)
- EXERCISE - II (MOTIONAL EMF)
- EXERCISE - II (SELF INDUCTANCE AND MUTUAL INDUCTANCE)
- EXERCISE-IA
- EXERCISE-IB
- EXERCISE-II
- EXERCISE-III
- PRACTICE EXERCISE (MAGNETIC FLUX, FARADAY.S LAW, LENZ.S LAW , AC GENERATOR)
- PRACTICE EXERCISE (MOTIONAL EMF)
- PRACTICE EXERCISE (SELF INDUCTANCE AND MUTUAL INDUCTANCE)
- PROBLEM
- Problems (Level-I)
- Problems (Level-II)