Complete Solutions to EXERCISE-2 (Addition, Subtraction and Resolution) of chapter MOTION IN A PLANE of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MOTION IN A PLANE |
| AAKASH SERIES | EXERCISE-2 (Addition, Subtraction and Resolution) |
| Number Of Questions | 29 |
| Academic Year | 2023-24 |
A person runs along a circular path of radius 5 m. If he completes half of the circle find the magnitude of the displacement vector, How far the person ran ?
View SolutionA car makes a displacement of 100 m towards east and then 200 m towards north. Find the magnitude and direction of the resultant.
View SolutionIf `vecA = 3hati - 4hatj` and `vecB=-hati - 4hatj` calculate the direction of `vecA + vecB`
View SolutionTwo vectors are given `vec(a) = -2hat(i) + hat(j) - 3hat(k)` and `vec(b) = 5hat(i) + 3hat(j) - 2hat(k)`. If `3hat(a) + 2vec(b) - vec(c) = 0` then third vector `vec(c)` is
View SolutionOne of the rectangular components of a velocity of 20 `ms^(-1)` is 10 `ms^(-1)`. Find the other component.
View SolutionA car weighing 100kg is on a slope that makes an angle 30° with the horizontal. The component of car's weight parallel to the slope is
`(g =10ms^(-2))`
View SolutionTo go from town A to town B a plane must fly about 1780 km at an angle of 30° West of North. How far north of A is B ?
View SolutionTwo vectors a and b have equal magnitudes of 12 units. These vectors are making angles `30^(@) and 120^(@)` with the x axis respectively. Their sum is `vecr`. Find the and y components of `vecr`.
View SolutionAngle (in rad) made by the vector `sqrt(3)hati+hatj` with the x-axis is
View SolutionA bird moves in such a way that it has a displacement of 12 m towards east, 5 m towards north and 9 m vertically upwards. Find the magnitude of its displacement
View SolutionThe direction cosines of a vector `vecA` are `cos alpha=(4)/(5sqrt(2)),cos beta =(1)/(sqrt(2)) and cos gamma=(3)/(5sqrt(2))` then the vector `vecA` is
View SolutionIf `vecP=hati+2hatj+6hatk` tits direction cosines are
View SolutionIf `vecA=2hati-3hatj+4hatk` its components in yz plane and zx plane are resectively
View SolutionIf vectors `vecA and vecB` are `3hati - 4hatj + 5hatk and 2hati + 3hatj -4hatk` respectively then find the unit vector parallel to `vecA+vecB`
View SolutionA vector `3hati+4hatj` rotates about its tail through an angle `37^(@)` in anticlockwise direction then the new vector is
View SolutionMaximum and minimum magnitudes of the resultant of two vectors of magnitudes P and Q are found to be in the ratio 3:1. Which of the following relations is true ?
View SolutionThe resultant of two equal forces is 141.4N when they are mutually perpendicular. When they are inclined at an angle `120^(@)`, then the resultant force will be
View SolutionThe magnitudes of two vectors `vecP and vecQ` differ by 1. The magnitude of their resultant makes an angle of `tan^(-1) (3//4)` with P. The angle between P and Q is
View SolutionGiven a +b+c+d=0 which of the following statement is incorrect
View SolutionThe resultant of two forces 2P and `sqrt(2) P` is `sqrt(10)` P. The angle between the forces is
View SolutionEleven forces each equal to 5N act on a particle simultaneously. If each force makes an angle `30^(@)` with the next one, the resultant of all forces is
View SolutionWhich of the following sets of forces acting simultaneously on a particle keep it in equilibrium?
View SolutionThe resultant of two forces 1 and Pis perpendi cular to 'l' and equal to 1. What is the value of 'P' and angle between
View SolutionIf the sum of two unit vectors is also a vector of unit magnitude, the magnitude of the difference of the two unit vectors is
View SolutionIf `vecP + vecQ = vecR` and `vecP - vecQ = vecS` , then `R^(2) + S^(2)` is equal to
View SolutionThe greater and least resultant of two forces are 7 N and 3 N respectively. If each of the force is increased by 3N and applied at 60°. The magnitude of the resultant is
View SolutionTwo forces are such that the sum of their magnitudes is 18 N, the resultant is `sqrt(228)` when they are at `120^(@)`. Then the magnitude of the forces are
View SolutionFigure shows three vectors `veca, vecb and vecc`, where R is the midpoint of PQ. Then which of the following relations is correct?
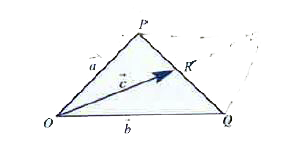
View SolutionThe resultant of two vectors `vecP and vecQ` is `vecR` If the magnitude of `vecQ` is doubled, the new resultant becomes perpendicular to `vecP`, the the magnitude of `vecR` is
View Solution
EXERCISE-2 (Addition, Subtraction and Resolution) questions and complete solutions for chapter MOTION IN A PLANE of JEE (MAIN AND ADVANCED) PHYSICS of Class 12
All Exercises from AAKASH SERIES Class 12 PHYSICS MOTION IN A PLANE
- EXERCISE-2 ( Relative velocity)
- EXERCISE-2 (A boat in a river)
- EXERCISE-2 (Addition, Subtraction and Resolution)
- EXERCISE-2 (Circular motion)
- EXERCISE-2 (Horizontal projectile motion)
- EXERCISE-2 (Lami.s theorem :)
- EXERCISE-2 (Oblique project
- EXERCISE-3 (A boat in a river)
- EXERCISE-3 (Circular Motion)
- EXERCISE-3 (Lamni.s theorem)
- EXERCISE-3 (Motion in a plane)
- EXERCISE-3 (Oblique projection )
- EXERCISE-3 (Parallelogram law, triangle law, polygon law)
- EXERCISE-3 (Relative velocity)
- EXERCISE-A (Motion in plane)
- EXERCISE-A ( Vector & scalar)
- EXERCISE-A (Addition & Subtractions of Vectors)
- EXERCISE-A (Ascending & descending Order)
- EXERCISE-A (circular motion)
- EXERCISE-A (Lami.s Theorem )
- EXERCISE-A (Matching)
- EXERCISE-A (Projections)
- EXERCISE-A (Relative velocity)
- EXERCISE-A (Resolution, motion in plane and motion of boat
- EXERCISE-A (Vectors & Scalars)
- EXERCISE-IB (Addition and subtraction of vectors)
- EXERCISE-IB (Circular motion)
- EXERCISE-IB (Motion in a plane )
- EXERCISE-IB (Projectile motion)
- EXERCISE-IB (Relative velocity )
- EXERCISE-IB (Resolution of vectors )
- EXERCISE-IB (Vectors and Scalars)
- PROBLEM