Complete Solutions to EXERCISE-3 (Oblique projection ) of chapter MOTION IN A PLANE of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MOTION IN A PLANE |
| AAKASH SERIES | EXERCISE-3 (Oblique projection ) |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
A projectile is thrown at an angle of `30^(@)` with a velocity of 10m/s. the change in velocity during the time interval in which it reaches the highest point is
View SolutionA body projected obliquely with velocity `19.6ms^(-1)` has its kinetic energy at the maximum height equal to 3 times its potential energy there. Its position after tsecond of projection from the ground is (h = maximum height)
View SolutionIt is possible to project a particle with a given speed in two possible ways so that it has the same horizontal range 'R'. The product of time taken by it in the two possible ways is
View SolutionA ball A is projected from the ground such that its horizontal range is maximum. Another ball B is dropped from a height equal to the maximum range of A. The ratio of the time of flight of A to the time of fall of B is
View SolutionA particle is projected from the ground with velocity u making an angle `theta` with the horizontal. At half of its maximum heights,
View SolutionA hose pipe lying on the ground shoots stream of water upward at an angle `60^(@)` to the horizontal at a speed of `20ms^(-1)`. The water strikes a wall 20m away at a height of `(g=10ms^(-2))`
View SolutionA body is projected with a velocity u at an A body is projected with a velocity u at anangle of `60^(@)` to the horizontal. The time interval after which it will be moving in a direction of `30^(@)` to the horizontal is
View SolutionA body of mass 2kg is projected from the ground with a velocity `20ms^(-1)` at an angle `30^(@)` with the vertical. If `t_(1)` is the time in seconds at which the body is projected and `t_(2)` is the time in seconds at which it reaches the ground, the change in momentum in `kgms^(-1)` during the time `(t_(2)-t_(1))` is
View SolutionThe maximum distance to which a man can throw a ball by projecting it horizontally from a height h is h. The maximum distance to which he can throw it vertically up is
View SolutionA body projected at `45^(@)` with a velocity of 20 m/s has a range of 10m. The decrease in range due to air resistance is `(g=10ms^(-1))`
View SolutionA particle is projected from the ground with an initial speed of v at an angle of projection `theta`. The average velocity of the particle between its time of projection and time it reaches highest point of trajectory is (2013 E)
View SolutionA ball is projected with `20sqrt2` m/s at angle `45^(@)` with horizontal. The angular velocity of the particle at highest point of its journey about point of projection is
View SolutionTwo seconds after projection, a projectile is moving at `30^(@)` above the horizontal. After one more second it is moving horizontally. If `g=10ms^(2)`, the velocity of projection is
View SolutionA stone is projected from the top of a tower with velocity `20ms^(-1)` making an angle `30^(@)` with the horizontal. If the total time of flight is 5s and `g=10ms^(-2)`
View SolutionIt is possible to project a particle with a given velocity in two possible ways so as to make them pass through a point P at a horizontal distancc r from the point of projection. If `t_(1)` and `t_(2)` are times taken to reach this point in two possible ways, then the product `t_(1)t_(2)` is proportional to
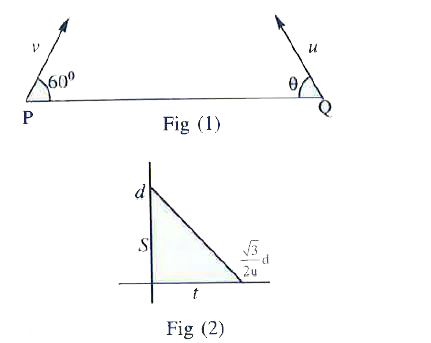
View SolutionA two particles P and Q are separated by distance d apart. P and Q move with velocity v and u making an angle `60^(@)` and `theta` with line PQ the graph between their relative separation (s) when time t is shown in figure (2). The velocity v in terms of u
View SolutionThe direction of projectile at certain instant is inclined at angle `alpha` to the horizontal. After t sec, if it is inclined at an angle `beta` then the horizontal component of velocity is
View SolutionIf `v_(1)` and `v_(2)` be the velocities at the end of focal chord of projectile path and u is the velocity at the vertex of the path, then
View SolutionA projectile fired with velocity u at right angle to the slope which is inclined at an angle `theta` with horizontal. The expression for R is
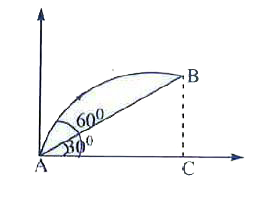
View SolutionIn figure shown below, the time taken by the projectile to reach from A to B is t then, the distance AB is equal to
View SolutionAt a certain height a body at rest explodes into two equal fragments with one fragment receiving a horizontal velocity of `10ms^(-1)`. The time interval after the explosion for which the velocity vectors of the two fragments become perpendicular to each other is `(g=10ms^(-2))`
View SolutionIn this above problem the horizontal distance between the two fragments when their velocity vectors are perpendicular to each other is
View SolutionIn the above problem, the time taken by the displacement vectors of the two fragments to become perpendicular to each other is
View SolutionIn the above problem, this horizontal distance between the two fragments when their position vectors are perpendicular to each other is
View SolutionAt a certain height a shell at rest explodes into two equal fragments. One of the fragments receives a horizontal velocity u. The time interval after which, the velocity vectors will be inclined at `120^(@)` to each other is
View Solution
EXERCISE-3 (Oblique projection ) questions and complete solutions for chapter MOTION IN A PLANE of JEE (MAIN AND ADVANCED) PHYSICS of Class 12
All Exercises from AAKASH SERIES Class 12 PHYSICS MOTION IN A PLANE
- EXERCISE-2 ( Relative velocity)
- EXERCISE-2 (A boat in a river)
- EXERCISE-2 (Addition, Subtraction and Resolution)
- EXERCISE-2 (Circular motion)
- EXERCISE-2 (Horizontal projectile motion)
- EXERCISE-2 (Lami.s theorem :)
- EXERCISE-2 (Oblique project
- EXERCISE-3 (A boat in a river)
- EXERCISE-3 (Circular Motion)
- EXERCISE-3 (Lamni.s theorem)
- EXERCISE-3 (Motion in a plane)
- EXERCISE-3 (Oblique projection )
- EXERCISE-3 (Parallelogram law, triangle law, polygon law)
- EXERCISE-3 (Relative velocity)
- EXERCISE-A (Motion in plane)
- EXERCISE-A ( Vector & scalar)
- EXERCISE-A (Addition & Subtractions of Vectors)
- EXERCISE-A (Ascending & descending Order)
- EXERCISE-A (circular motion)
- EXERCISE-A (Lami.s Theorem )
- EXERCISE-A (Matching)
- EXERCISE-A (Projections)
- EXERCISE-A (Relative velocity)
- EXERCISE-A (Resolution, motion in plane and motion of boat
- EXERCISE-A (Vectors & Scalars)
- EXERCISE-IB (Addition and subtraction of vectors)
- EXERCISE-IB (Circular motion)
- EXERCISE-IB (Motion in a plane )
- EXERCISE-IB (Projectile motion)
- EXERCISE-IB (Relative velocity )
- EXERCISE-IB (Resolution of vectors )
- EXERCISE-IB (Vectors and Scalars)
- PROBLEM