Complete Solutions to EXERCISE - II of chapter RANDOM VARIABLE of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | RANDOM VARIABLE |
| AAKASH SERIES | EXERCISE - II |
| Number Of Questions | 76 |
| Academic Year | 2023-24 |
A person who tosses an unbiased coin gains two points for turning up a head and loses one point for a tail. If three coins are tossed and the total score X is observed, then the range of X is
View SolutionA random variable X has the following distribution
`{:(X=x_(1):,1,2,3,4),(P(X=x_(1)):,k,2k,3k,4k):}`
The value of k and `P(X lt 3)` are equal to
View SolutionThe probability distribution of a random variable is given below:
`{:(X=x,0,1,2,3,4,5,6,7),(P(X=x),0,k,2k,2k,3k,k^(2),2k^(2),7k^(2)+k):}`
Then `P(0 lt X lt 5)=`
View SolutionA random variable x had its range {0, 1, 2} and the probabilities are given by `P(x=0)=3k^(3), P(x=1)=4k-10k^(2), P(x=2)=5kk-1` where k is constant then k =
View SolutionThe value of c for which `P(x=k)=ck^(2)` can serve as the probability distribution function of a random variable X that takes values 0, 1, 2, 3, 4 is
View SolutionThe range of random vairable `x={1, 2, 3 …..}` and the probabilities are given by `P(x=k)=(c^(k))/(k!)` then c =
View SolutionThe range of random variable `x={1, 2, 3….}` and the probabilities are given by `P(x=k)=(3^(CK))/(K!)` (k = 1, 2, 3, ……) and C is a constant. Then C =
View SolutionIf the range of a random variable X is {0,1,2,3,4,……….} with `P(X=k)=((k+1))/(3^(k))` for `k ge0`, then u=
View SolutionA random variable x takes the values 0, 1, 2, 3 and its mean is 1.3. If P(x=3)=2 P(x=1) and P(x=2)=0.3, then P(x=0)=
View SolutionIf X is a random variable with the following probability distribution
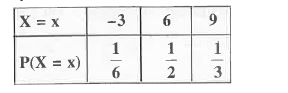
then the variance of X is
View SolutionA die a rolled and let x denote twice the number appearing on its face. Mean of x is
View SolutionA pair of dice is thrown at a time. X is the maximum of the two numbers shown on the dice. Then mean of X is
View SolutionA sample of 2 itmes is selected at random from a bag containing 5 items of which 2 are defective. Then mean of number of defective items is
View SolutionA player tosses two coins. He wins Rs. 1 if 1 head appears, Rs 2 if 2 heads appear. But he lose Rs 5 if no head appears. The mean of the prized money is
View SolutionLet X denote the profit of a business man. The probability of getting profit `Rs. 3000` is 0.6. The probability of getting loss `Rs 4000 ` is 0.3. The probability of getting neither profit nor loss is 0.1 . The mean and variance of X are
View SolutionThe random variable takes the values 1,2,3,…….m. If `P(X=n)=(1)/(m)` to each n, then the variance of X is
View SolutionTwo cards are drawn successively one by one with out replacement from a pack of cards. The mean of number of kings is
View SolutionA : If the difference between the mean and variance of a binomial distribution for 5 trials is `5//9` then the distribution o is `(2//3+1//3)^(5)`
R : The binomial distribution with parameters n, p is `(q+p)^(n)`
View SolutionIf the standerd deviation of the binomial distribution `(q+p)^(16)` is 2, then mean is
View SolutionIf a binomial distribution has mean 2.4 and variance is 1.44, then n=
View SolutionIf the mean of a binomial distribution with 9 trials is 6, then its variance is
View SolutionIf the mean of the binomial distribution is 100. Then standard deviation lies in the interval
View SolutionFour bad apples are mixed accidentally with 20 good apples. Probability distribution of the number of bad apples in a draw of 2 apples with replacement is formed. The mean is
View SolutionTwo cards are drawn successively with replacement . The mean of number of Aces is
View SolutionThe mean and variance of a random variable X having binomial distribution are 4 and 2 respectively. Then `P(x gt 6)=`
View SolutionThe least number of times a fair coin must be tossed so that the probability of getting atleast one head is atleast 0.8 is
View SolutionThe probabilty of hitting a target is 1/3. The least number of times to fire so that the probability of hitting the larget atleast once is more than `90%` is
View SolutionThe mean and variance of a random variable X having a binomial distribution are 4 and 2 respectively, then P(X=1) is
Theoretical Distributions
View SolutionIn a binomial distribution, mean = 25, variance = 20 then `P(X le 100)=`
View SolutionIf the mean and variance of a binomial variable X are 2 and 1 respectively, then `P(X ge1)=`
View SolutionX is a binomial variate with parameters `n=6` and p. If `4P(X=4)=P(X=2)`, then p is s
View SolutionFor a binomial variate X if `n=5,` and P(X=1)=8P(X=3), thenp=
View SolutionX follows a binomial distribution with parameters n and p where `0 lt p lt 1`.
If `(P(X=r))/(P(X=n-r))` is independent of n and r then p=
View SolutionSuppose X is binomial distribution with parameters n = 100 and p = 1/2 then P(X=r) is maximum when r =
View SolutionSuppose X is a binomial distribution with parameters n = 100 and `p=(1)/(3)` then P(x=r) is maximum when r =
View SolutionA coin is tossed any number of times until a head appears. If x donotes the number of tosses till head uappear then `P(x ge 3)=`
View SolutionA fair coin is tossed n times. Let x be random variable denoting the number of heads tossed. If `P(x=4), P(x=5),P(x=6)` are in A.P. then n =
View SolutionWhen a coin is tossed n times, if the probability for getting 6 heads is equal to the probability of getting 8 heads, then the value of n is
View SolutionOne hundred identical coins each with probability p showing up heads are tossed once. `"If" 0 lt p lt 1` and the probability of heads showing on 50 coins is rqual to that of heads showing on 51 coins, then the value of p is
View SolutionA die is rolled 3 times. If getting a one is considered as a success, then the probability of 2 successes is
View SolutionAn unbiased die is tossed 6 times. The mean of number odd numbers is
View SolutionIn a binomial distribution `B(n,p=(1)/(4))`, if the probability of at least one success is greater than or equal to `9//10`, then n is greater than
View SolutionA die is thrown (2n + 1) times. The probability of getting 1 or 3 or 4 atmost n times is
View SolutionIf X is a binomial variate with n = 7 and `P(X=3)=P(X=4)` then `P(X=5)=`
View SolutionFor a binomial variate X with `n=6`, if `P(X=2)=9P(X=4)`, then its variance is
View SolutionThe probability that a candidate seeure a seat in Engineering through EAMCET is `1//10`. Seven candidates are selected at random from a centre. The probability that exactly two will get seats is
View SolutionThe probability that a bomb dropped from a plane strikes the target is `1//5`. The probability that out of six bombs dropped at least 2 bombs stricke the target is
View SolutionAn experiment succeeds twice as often as it fails. The probability of at least 5 successes in the six trials of this experiment is
View SolutionIn an average , rain falls on 12 days in every 30 days. The probability that , rain will fall on just 3 days of a given week is
View SolutionSuppose A and B are two equally strong table tennis players . The probability that A beats B in exactly 3 games out of 4 is
View SolutionThe probability that a man can hit a target is `3//4`. He makes 5 trials. The probability that he will hit the target every time he hits is
View SolutionA box contains tickets numbered from 1 to 20. If 3 tickets are drawn one by one with replacement then the probability of getting prime number exactly 2 times is
View SolutionIf on an average 1 vessel in every 10 is wrecked, the chance that out of 5 vessels expected 4 at least will arrive sefely is
View SolutionOne in 9 ships is likely to be wrecked , when they are set on sail. When 6 ships set on sail, the probability for exactly, 3 will arrive safely is
View SolutionThe probability of happening of an event in a trial is 0.5. The probability of happening of the event atlest once if the experiment is repeated 3 times is
View SolutionThe probability that an event does not happen in one trial is 0.8 The probability that the event happens atmost once in three trials is
View Solution12 coins are tossed 4096 times. The number of times that one can get atleast 2 heads is
View SolutionFive coins are tossed 3200 times. The number of times getting exactly two heads is
View SolutionA poisson variate x is such that `P(x=2)=9P(x=4)+90.P(x=6)` then mean and standard deviation are
View SolutionSuppose on an average 1 house in 1000 in a certain district has a fire during a year . If there are 2000 houses in the district , then the probability that exactly 5 houses will have a fire during the year is
View SolutionA manufacturing concern emplyoing a large number of workers over a period of time and the average absentee rate is 2 workers per shift then probability that exactly two workers will be absent is
View SolutionIf the number of telephone calls an operator receives between 10.00 pm to 10.10 pm follow poisson distribution with mean 3. The probability that the operator receives one call during that interval the next day is
View SolutionThe probability that an individual suffers a bad reaction from an injection is 0.001. The probability that out of 2000 individuals more than 2 suffer a bad reaction is
View SolutionSuppose there are 500 misprints in a book of 750 pages. Assuming that the number of misprints per page is a poisson random variate. The probability that a page selected at random has more than one mis print is
View SolutionIn a book of 500 pages , it is found that there are 250 typing errors . Assume that Poisson law holds for the number of errors per page . Then, the probability that a random sample of 2 pages will contains no error is
View SolutionA firm hires out 3 cars every day. The demand for a car on each day is distributed as a poisson distribution with mean 2.0. The probability that some demand is refused on a day is `(e^(-2)=0.135)`
View SolutionSix coins are tossed 6400 times. The probability of getting 6 heads x times using poisson distribution is
View SolutionSix coins are tossed 9600 times. The probability of getting 5 heads 2 times, by using poisson distribution, is
View SolutionCycle tyres are supplied in lots of 10 and there is a chance of 1 in 500 tyres to be defective. Using Poisson's distribution the approximate number of lots containing no defective tyres in a consignment of 10,000 lots is e^-0.02=0.9802
View SolutionIn a poisson distribution, the variance is m. The sum of terms in odd places in the distribution is
View SolutionA random variable x follows binomial distribution with mean a and variance b then observe the following statements.
Statement-I : `a gt b gt 0`
Statement-II : `(a^(2))/(a-b)` is a positive integer
Statement-III : `a+b=1`
which of the above statments are true.
View SolutionA fair coin is tossed n times and x be the number of heads. If P(x=4), P(x=5), P(x=6) are in A.P. then which of the following are correct.
Statement-I : n = 7 Statement-II : n = 9
Statement-III : n = 2 Statement-IV : n = 14
correct statements are
View SolutionA random variable has the following distribution.
`{:(x=x_(i),,-3,,-2,,-1,,0,,1,,2),(P(x=x_(i)),,0.1,,2K,,3K,,7K,,0.2,,0.1):}`
Then for the values, A = K, B = Mean, C = Variance, the ascending order is
View SolutionOne hundred indentical coins are thrown as each coin has the probability of head as p. Let x = number of coins showing heads then match the following conditions with p value.
(A) `P(x=49)=P(x=50)" "1)" "P=(1)/(2)`
(B) `P(x=48)=P(x=52)" "2)" "(51)/(101)`
( C ) `P(x=r)=P(x=n-r)" "3)" "(50)/(101)`
`" "4)" "(57)/(100)`
The correct matching is
View SolutionObserve the following statements
Assertion (A) : X is binomial variate with parameters `2n+1` and p = 1/2 then P(x = odd values) = 1/2
Reason ( R ) : If `""^(n)C_(r)=C_(r)` then
`C_(1)+C_(3)+C_(5)+……=2^(n-1)`. Then
View SolutionX is a poisson variate with parameter `lambda`. Then match the following.
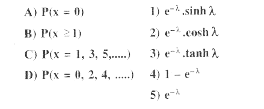
The correct matching is
View Solution
EXERCISE - II questions and complete solutions for chapter RANDOM VARIABLE of JEE (MAIN AND ADVANCED) MATHEMATICS of Class 12