Complete Solutions to EXAMPLES of chapter RANDOM VARIABLE of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | RANDOM VARIABLE |
| AAKASH SERIES | EXAMPLES |
| Number Of Questions | 36 |
| Academic Year | 2023-24 |
Find the area of the figure given below.
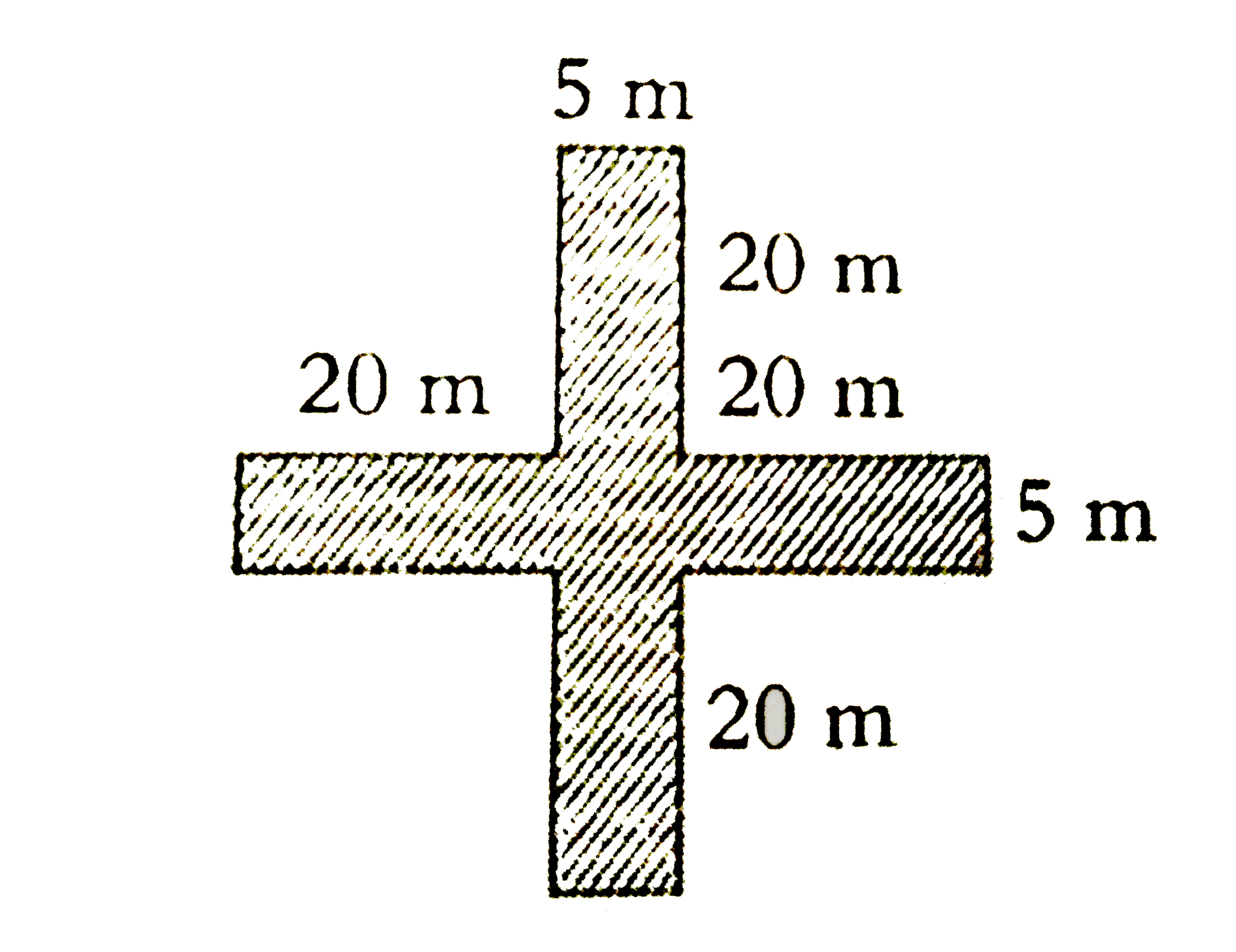
View SolutionFind the mean and variance of the random variable X which follows the following distribution.

View SolutionFind the mean and variance of the random variable X whose distribution is

View SolutionIf X is a random variable with the following distribution

where `p+q=1` then show that the variance of X is `pq(a-b)^(2)`.
View SolutionLet X be a random variable such that `P(X=-2)=P(X-1)=P(X=2)=P(X=1)=(1)/(6)` and `P(X=0)=(1)/(3)`. Find the mean and variance of X.
View SolutionFind the constant C, so that
`F(x)=C((2)/(3))^(x),x=1,2,3………………` is the p.d.f of a discrete random variable X.
View SolutionA cubical die is thrown. Find the Mean and variance of X, giving the number on the face that shows up.
View SolutionThe probabilities of outcomes of a random experiment are given below :
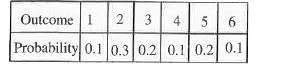
Let = {2, 4, 6}, B = {1, 2, 3, 4} and C = {1, 2}. Then find P(A), P(B), P( C ), `P(A nn B), P(B nn C)` and `P(C nn A)`.
View SolutionIf `X~B(20,1//2)`. Find mean and variance.
View SolutionIf `X~B(n,p),mu=20,sigma^(2)=10`, then find n and p.
View SolutionIf for a Binomial distribution, `mu=10` and `sigma^(2)=5`, then find `P(X gt 6)`.
View SolutionFor the binomial distribution X with parameters `n=12,p=(1)/(2)`, compute
i) `P(10leXle12)" "`ii) `P(3 lt X lt 6)`
View SolutionIf 3 coins are tossed simultaneously and the number of heads turned up is denoted by the variable X, then find mean and variance of X.
View SolutionWhen a coin is tossed n times, if the probability for getting 6 heads is equal to the probability of getting 8 heads, then the value of n is
View SolutionThe least number of times a fair coin must be tossed so that the probability of getting atleast one head is atleast 0.8 is
View SolutionFind the probability of guessing correctly atleast 6 out of 10 questions in (i) True or false type examination (ii) multiple choice with 4 possible answers.
View SolutionIn a box containing 15 bulbs, 5 are defective. If 5 bulbs are selected at random from the box, the probability of the event that
(i) none of them is defective is `12/143`
(ii) only one of them is defective is `50/143`
(iii) atleast one of them is defective is `131/143`
View SolutionFive coins are tossed 320 times. Find the frequencies of the distribution of number of heads and tabulate the result.
View SolutionFor a poisson variate X, P(X = 2) = P(X = 3) find variance of X.
View SolutionIf X is a poisson variate such that `P(X=0)=P(X=1)=K`, then show that K = 1/e
View SolutionSuppose that a random variable X follows Poisson distribution . If P(X=1)=P(X=2)then P(X=5)=
View SolutionThe number of persons joining a cinema ticket counter in a minute has poisson distribution with parameter 6. Find the probability that (i) no one joins the queue in a particular minute (ii) two or more persons join the queue in a minute
View SolutionNumber of errors on a single page has poisson distribution with average number of errors per page is one. Find the probability that there is atleast one error on a page.
View SolutionNumber of accidents on a national highway each day is a poisson variable with an average of three accidents per a day. Find the probability that no accidents will occur on a given day.
View SolutionIn a large consignment of apples are rotten. What is the probability that a carton of 48 apples contain less than two rotten ones ? Answer the questions using
(i) Binomial distribution
(ii) Poisson distribution
View SolutionA factory produces lazor blades and 1 in 500 blades is estimated to be defective. The blades are supplied in packets of 10. In a consignment of 10,000 packets, using poisson distribution, find approximately the number of packets which contain no defective blades.
View SolutionFive coins are tossed 3200 times. Using the Poisson distribution , the approximate probability of getting five heads 2 times is
View SolutionTwo cards are drawn successively with replacement from a pack of cards. Taking the random variable X = the number of kings, find the probability distribution of X. Also find mean and variance of X.
View SolutionA pair of fair dice is rolled at a time. The random variable X is the maximum of the two numbers shows on the dice. Find the probability distribution of X and mean of X.
View SolutionLet X be a B(2, p) and Y be an independent B(4, p). If `P(X ge 1)=5//9`, then find `P(Y ge1)`.
View SolutionIn a binomial distribution, n=5, the sum of the mean and variance is 1.8 . Then the distribution is
View SolutionIf for a binomial distribution, the mean is 10 and the variance is 5, then find the parameters and `P(X gt 6)`.
View SolutionA and B throw one die for a stake of Rs 11 which is to be won by the player who first throws 6. If A has the first throw, what are their respective expectations ?
View SolutionA person gets dollars eqal to the square of the number which comes up when a balanced die, with faces marked 1, 2, 3, 4, 5, 6 is rooled one. If the game is repeated an indefinitely large number of times, how much money can be expect in the long run per game ?
View SolutionA coin is tossed until a head appears. What is the expectation of the number of tosses required ?
View SolutionA player tosses 3 fair coins and wins Rs. 8 if three heads occur, Rs. 3 if 2 heads occur and Rs. 1 if one head occurs. If the game as to be fair (i.e., expected value is zero) how must should he lose, if no head occur ?
View Solution
EXAMPLES questions and complete solutions for chapter RANDOM VARIABLE of JEE (MAIN AND ADVANCED) MATHEMATICS of Class 12