Complete Solutions to ADDITIONAL EXERCISE of chapter RANDOM VARIABLE of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | RANDOM VARIABLE |
| AAKASH SERIES | ADDITIONAL EXERCISE |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
The probability function of a random variable X is given by
`p(x)=(1)/(3)`, if x = -1, 0, 1
=0, otherwise.
Find the distribution function of X.
View SolutionA random variable X has the following probability distribution :

(i) determine the value of a
(ii) find `P(X lt 3),P(X gt 3)`
View Solution
is the probability distribution of a random variable X. Find the variance of X.
View SolutionCompute the variance of X whose distribution is given by
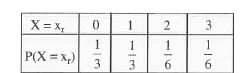
View SolutionState whether the following probability distribution is admissible or not.
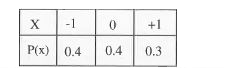
View SolutionState whether the following probability distribution is admissible or not.
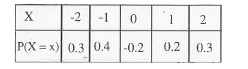
View SolutionFour bad apples are mixed accidentally with 20 good apples. Probability distribution of the number of bad apples in a draw of 2 apples with replacement is formed. The mean is
View SolutionA business man gets a profit of Rs. 2800 with probability 0.5, loss of Rs. 5000 with probability 0.3. and neither profit nor loss with probability 0.2. Find mean of his income.
View SolutionA pair of fair dice is rolled 2 times. Find the mean of the number of doublets on the dice. Find also variance of the number of doublets on the dice.
View SolutionA coin is loaded such that `P(H)=3P(T)`. It is tossed 3 times. Let X be the random variable which indicates the number of heads which occur. Find the mean of X, variance of X.
View SolutionIn a binomial distribution the sum and difference of mean and variance are 1.8 and 0.2 respectively. Find the parameters.
View SolutionIf X is a binomial variate with mean 10 and variance 5 then find `P(X le 1)`.
View SolutionA man takes a step forward with probability 0.4 and backward with probability 0.6. The probability that at the end of eleven steps, he is just one step away from the starting point is
View SolutionOn an average 1 in 100 razor blades manufactured by a firm are defective.If blades are supplied in packets of 5 each, find the probability that a packet has atleast one defective blade. If 1000 packets are tested, in how many packets would you expect defective blades.
View SolutionThe following data is related to the number of mistakes in each page of a book containing 180 pages :

Fit a Poisson distribution to the data. Obtain the theoretical frequencies.
View SolutionEvery one out of 15 telephone calls between 2.00 p.m and 4.00 p.m. in a week is busy. Find the probability that out of 6 randomly chosen telephone numbers,
(i) exactly two are busy
(ii) atleast three of them are busy.
View SolutionIf a person gains or loses an amount equal to the number appearing when an unbiased die is rolled once, according to wether the number is even or odd, how much money can he expect per game in the long run ?
View SolutionA person gets Rs. 2 if head comes and loses Rs. 5 when a tail comes then how much money can he expect in the long run per game, when an unbiased coin in tossed twice.
View SolutionA person gets Rs. `(2X+3)` where X denotes the number appearing when a balaced die is rolled once, how much money can be expect in the long run per game ?
View SolutionA coin is tossed until a tail appears what is the expectation of the number of tosses ?
View SolutionSuppose that X is a ramdom variable for which `E(X)=10` and Var (X) = 25. Find the values of a and b such that Y = ax - b has expectation 0 and variance 1.
View SolutionGiven the following table

Computer i) `E(4X+5)` ii) `E(X^(2))`
iii) V(X) iv) `V(2X+-3)`
View SolutionA ramdom variable X can assume any positive integral value of n with a probability proportional to n with a probability proportional to `(1)/(3^(n))`. Find the expectation of X?
View SolutionFind the probability of guessing at least 6 out of 10 answers in
i) True false type examination
ii) Multiple choice with 4 possible answers
View SolutionThee number of persons joining a cinema ticket counter is a minute has Poisson distribution with parameter 6. Find the probability that
i) no one joins the queue in a particular minute
ii) two or more persons join the queue is a minute.
View Solution
ADDITIONAL EXERCISE questions and complete solutions for chapter RANDOM VARIABLE of JEE (MAIN AND ADVANCED) MATHEMATICS of Class 12