Complete Solutions to MCQs of chapter MOTION IN A PLANE of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MOTION IN A PLANE |
| NCERT FINGERTIPS | MCQs |
| Number Of Questions | 92 |
| Academic Year | 2023-24 |
Which of the following is not a scalar quantity ? a) temperature b) Coefficient of friction c) charge d) Impulse
View SolutionIn Latin, the word vector means a) magnitude b) direction c) carrier d) cap
View SolutionA vector is not changed if
View SolutionWhich one of the following statements is false regarding the vectors ?
View SolutionWhich of the following pairs of vectors are parallel ?
View SolutionWhich of the following is not a property of a null vector ?
View SolutionGiven `vecA + vecB + vecC + vecD = vec0`, which of the following statements is not correct ?
View SolutionTwo vectors `vec(A) and vec(B)` inclined at an angle `theta` have a resultant `vec(R )` which makes an angle `alpha` with `vec(A)`. If the directions of `vec(A) and vec(B)` are interchanged, the resultant will have the same
View SolutionRain is falling vertically with a speed of `35 m s^(-1)` . A woman rides a bicycle with a speed of ` 12 m s^(-1)` in east to west direction. In which direction should she hold her umbrella ?
View SolutionA river is flowing due east with a speed `3ms^(-1)`. A swimmer can swim in still water at a speed of `4ms^(-1)`. If swimmer starts swimming due north, then the resultant velocity of the swimmer is a) 3 m/s b) 5 m/s c) 7 m/s d) 2 m/s
View SolutionIf `hatn` is a unit vector in the direction of the vector `vecA`, them :
View SolutionThe component of vector `vecA = 2hati + 3 hatj` along the direction of `(hati - hatj)` is
View SolutionThe magnitude of the x-component of vector `vec(A)` is 3 and the magnitude of vector `vec(A)` is 5. What is the magnitude of the y-component of vector `vec(A)` ?
View SolutionThe direction cosines of `hati + hatj + hatk` are
View SolutionIf `vec(A)` makes an angle `alpha, beta` and `gamma` from x,y and z axis respectively then `sin^(2)alpha+sin^(2) beta+sin^(2) gamma=`
View SolutionWhich of the following qauntities is dependent of the choice of orientation of coordinates axes?
View SolutionTwo vectors `vecA and vecB` inclined at an angle `theta` have a resultant `vecR` which makes an angle `alpha` with `vecA` and angle `beta` with `vecB`. Let the magnitudes of the vectors `vecA, vecB and vecR` be represented by A, B and R respectively. Which of the following relations is not correct ?
View SolutionVectors `vecA` and `vecB` include an angle `theta` between them. If `(vecA + vecB)` and `(vecA- vecB)` respectively subtend angles `alpha and beta` with `vecA`, then `(tan alpha + tan beta)` is
View SolutionA unit vector in the direction of resultant vector of `vecA = -2hati + 3hatj + hatk and vecB = hati + 2 hatj - 4 hatk` is
View SolutionIn the question number 20, a unit vector perpendicular to the direction of `vecA and vecB ` is
View SolutionResultant of two vectors `vecA and vecB` is of magnitude P, If `vecB` is reversed, then resultant is of magnitude Q. What is the value of `P^(2) + Q^(2)` ?
View SolutionIf `|vecA + vecB| = |vecA - vecB|`, then the angle between `vecA and vecB` will be
View SolutionA motor boat is racing towards North at `25 km//h` and the water current in that region is `10 km//h` in the direction of `60 ^@` East of South. Find the resultant velocity of the boat.
View SolutionA magnitude of vector `vecA,vecB` and `vecC` are respectively `12, 5` and `13` units and `vecA+vecB=vecC` then the angle between `vecA` and `vecB` is
View SolutionThe driver of a car moving towards a rocket launching pad with a speed of 6 m `s^(-1)` observed that the rocket is moving with speed of 10 m `s^(-1)`. The upward speed of the rocket as seen by the stationery observer is nearly
View SolutionWhich of the following figure represents the force of `10 N` in a direction of `30^(@)` east of north?
View SolutionThe `(x, y, z)` coordinates of two points A and B are given respectively as `(0, 4, -2) and (-2, 8, -4)`. The displacement vector form A to B is
View SolutionA person moves 30 m north. Then 30 m east, then `30sqrt(2)` m south-west. His displacement from the original position is
View SolutionA bird flies from (-3m, 4m, -3 m) to (7m, -2m, -3m) in the xyz-coordinates. The bird's displacement vector is given by
View SolutionOn an open ground, a motorist follows a track that turns to his left by an angle of `60^(@)` after every `500 m`. Starting from a given turn, The path followed by the motorist is a regular hexagon with side `500 m`, as shown in the given figure specify the displacement of the motorist at the end of third turn
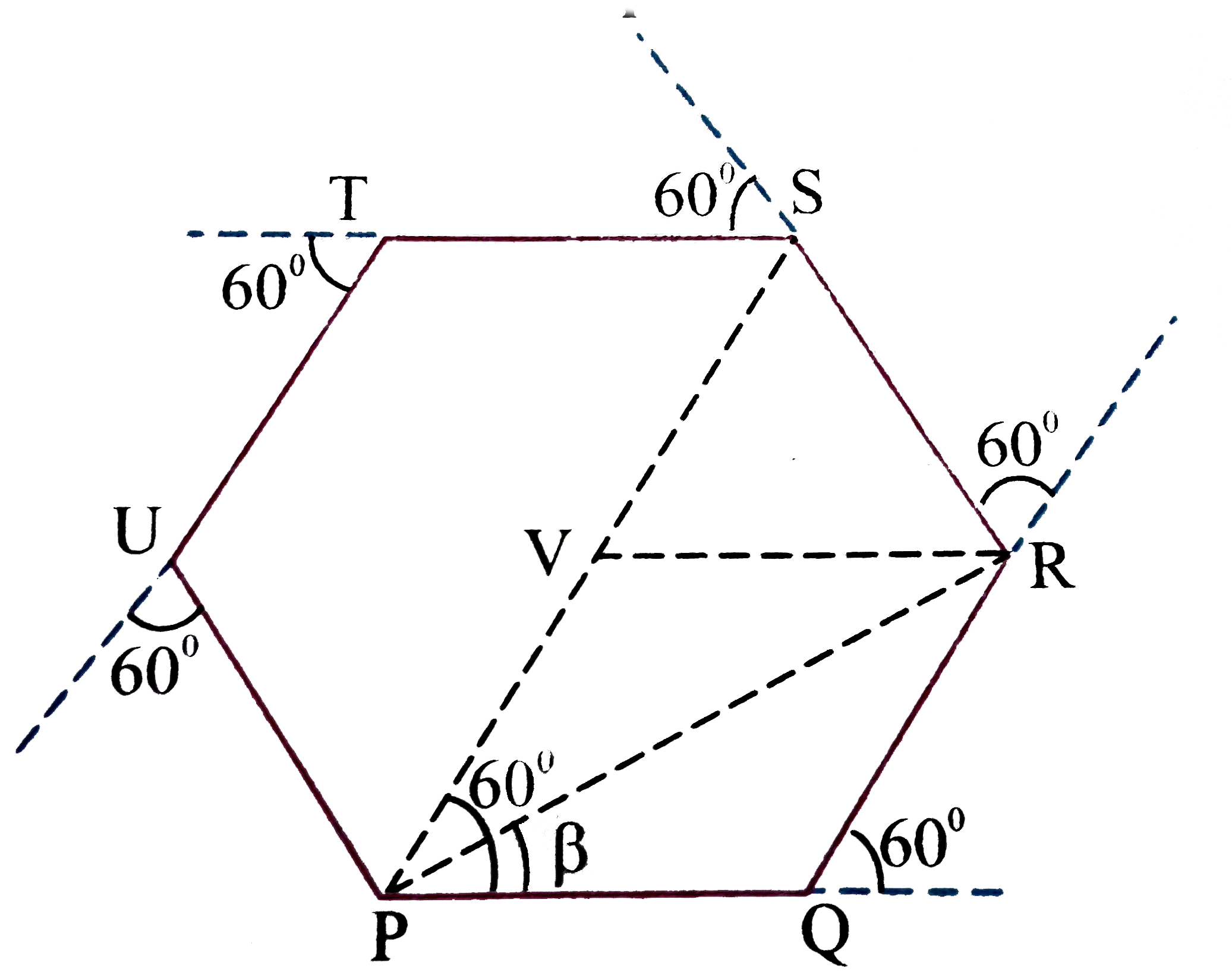
.
View SolutionA particle starts moving from point (2, 10, 1). Displacement for the particle is `8hati - 2hatj + hatk` . The final coordinates of the particle is
View SolutionFor any arbitrary motion in space, which of the following relations are true?
a) `v_("average") = (1//2)(v(t_(1) + v(t_(2))`
b) `v_("average") = [r(t_(2))-r(t_(1)]/(t_(2)-t_(1)`
`v(t) = v(0) + at`
d) `a_("average") = [v(t_(2))-v(t_(1))/[t_(2)-t_(1))`
The average stands for average of the quantity over time interval `t_(1)` to t_(2)`
View SolutionThe position of a particle is given by `vecr = 3t hati + 2t^(2) hatj + 5hatk`, where t is in seconds and the coefficients have the proper units for `vecr` to be in meters. The direction of velocity of the particle at `t = 1` s is
View SolutionIn the question number 35, the acceleration of the particle at `t = 1` is
View SolutionIf `x = 5t + 3t^(2)` and `y = 4t` are the x and y co-ordinates of a particle at any time t second where x and y are in metre, then the acceleration of the particle
View SolutionA particle starts from origin at `t=0` with a constant velocity `5hati m//s` and moves in `x-y` plane under action of a force which produce a constant acceleration of `(3hati+2hatj)m//s^(2)` the `y`-coordinate of the particle at the instant its `x` co-ordinate is `84 m` in `m` is
View SolutionIn the question number 38, the speed of the particle at this time is
View SolutionSuppose that two objects A and B are moving with velocities `vecv_(A)` and `vecv_(B)` (each with respect to some common frame of reference). Let `vecv_(AB)` represent the velocity of A with respect to B. Then
View SolutionRain is falling vertically with a speed of `30 m s^(-1)` . A woman rides a bicycle with a speed of ` 12 m s^(-1)` in east to west direction. In which direction should she hold her umbrella ?
View SolutionA girl riding a bicycle with a speed of ` 5 m//s` to wards Noth direction, observes rain falling vertically down. If she increases her speed to `10 m//s`, rain appeard to meet her at ` 45^@` to the vertical . What is the speed ot the rain ? In what direction does rain fall as observed by a ground based observer ?
View SolutionWhich of the following is true regarding projectile motion ?
View SolutionA bomb is released by a horizontal flying aeroplane. The trajectory of the bomb is
View SolutionIn case of a projectile motion, what is the angle between the velocity and acceleration at the highest point?
View SolutionIf a body is projected with an angle `theta` to the horizontal, then
View SolutionTwo particles are projected simultaneously in the same vertical plane from the same point, with different speeds `u_(1)` and `u_(2)`, making angles `theta_(1)` and `theta_(2)` respectively with the horizontal, such that `u_(1) cos theta_(1) = u_(2) cos theta_(2)`. The path followed by one, as seen by the other (as long as both are in flight), is
View SolutionA football is kicked into the air vertically upwards. What is its (a) acceleration, and (b) velocity at the highest point ?
View SolutionThe equations of motion of a projectile are given by `x=36tm and 2y =96t-9.8t^(2)m`. The angle of projection is
View SolutionThe relation between the time of flight of projectile `T_(f)` and the time to reach the maximum height `t_(m)` is
View SolutionFrom the top of a 490 m high cliff, a boy throws a stone horizontally with a initial speed of ` 15 ms^(-1)`. What is the time taken by the stone to reach the ground.
View SolutionIn the question number 52, the speed with which the stone hits the ground is
View SolutionTwo balls are projected at an angle `theta` and `(90^(@) - theta)` to the horizontal with the same speed. The ratio of their maximum vertical heights is
View SolutionTwo particls are projected in air with speed u at angles `theta_(1) and theta_(2)` (both acute) to the horizontal, respectively. If the height reached by the first particle is greater than that of the second, then which one of the following is correct? where `T_(1) and T_(2)` are the time of flight.
View SolutionThe ceiling of a hall is 40m high. For maximum horizontal distance, the angle at which the ball may be thrown with a speed of `56ms^(-1)` without hitting the ceiling of the hall is
View SolutionIn the question number 56, the maximum horizontal distance covered by the ball will be
View SolutionIf R and H represent horizontal range and maximum height of the projectile, then the angle of projection with the horizontal is
View SolutionWhen air resistance is taken into account while dealing with the motion of the projectile which of the following properties of the projectile, shows an increases?
View SolutionTwo projectiles are fired from the same point with the same speed at angles of projection `60^(@) and 30^(@)` respectively. Which one of the following is true?
View SolutionGalileo writes that for angles of projection of a projectile at angles `(45 + theta)` and `(45 - theta)`, the horizontal ranges described by the projectile are in the ratio of (if `theta le 45`)
View SolutionA cricket ball is thrown at a speed of 30 m `s^(-1)` in a direction `30^(@)` above the horizontal. The time taken by the ball to return to the same level is
View SolutionIn the question number 62, the distance from the thrower to the point where the ball returns to the same level is
View SolutionIn the question number 62. the maximum height attained by the ball is
View SolutionA cricketer can throw a ball to a maximum horizontal distance of 100m. With the same speed how much high above the ground can the cricketer throw the same ball?
View SolutionAn aeroplane flying horizontally with a speed of 360 km `h^(-1)` releases a bomb at a height of 490 m from the ground. If g = 9. 8 m `s^(-2)` , it will strike the ground at
View SolutionA ball is thrown from the top of a tower with an initial velocity of `10 m//s` at an angle of `30^(@)`above the horizontal. It hits the ground at a distance of 17.3 m from the base of the tower. The height of the tower `(g=10m//s^(2))` will be
View SolutionThe speed of a projectile at its maximum height is `sqrt3//2` times its initial speed. If the range of the projectile is n times the maximum height attained by it, n is equal to :
View SolutionFour bodies A,B,C and D are projected with equal velocities having angles of projection `15^(@),30^(@),45^(@) and 60^(@)` with the horizontal respectively. The body having the shortest range is
View SolutionA player kicks a ball at a speed of `20ms^(-1)` so that its horizontal range is maximum. Another players 24m away in the direction of kick starts running in the same direction at the same instant of hit. If he has to catch the ball just before it reaches the ground, he should run with a velocity equal to `(take g=10ms^(-2))`
View SolutionThe term centripetal acceleration was proposed by
View SolutionCentripetal acceleration is
View SolutionWhat is approximately the centripetal acceleration (in units of acceleration due to gravity on earth, g = 10 m `s^(-2)` of an air-craft flying at a speed of 400 m `s^(-1)` through a circular arc of radius 0.6 km ?
View SolutionVelocity vector and acceleration vector in a uniform circular motion are related as
View SolutionA body executing uniform circular motion has its position vector and acceleration vector
View SolutionFor a particle performing uniform circular motion, choose the incorrect statement form the following.
View SolutionWhich of the following statements is incorrect ?
View SolutionA particle is moving on a circular path of radius r with uniform speed v. What is the displacement of the particle after it has described an angle of `60^(@)`?
View SolutionA cyclist is riding with a speed of `27 km h^(-1)`. As he approaches a circular turn on the road of radius 80 m, he applies brakes and reduces his speed at the constant rate `0.5 ms^(-2)`. What is the magnitude and direction of the net acceleration of the cyclist on the circular turn ?
View SolutionA stone tied to the end of string 100cm long is whirled in a horizontal circle with a constant speed. If the stone makes 14 revolution in 22s, then the acceleration of the stone is
View SolutionAn insect trapped in circular groove of radius 12 cm moves along the groove steadily and completes 7 revolutions in 100s. The linear speed of the insect is
View SolutionA particle is moving on a circular path with a constant speed `v`. Its change of velocity as it moves from A to B is:

View Solution`vecA and vecB` are two vectors. `(vecA + vecB) xx (vecA - vecB)` can be expressed as :
View SolutionIf `vecA xx vecB = vecC+ vecD`, them select the correct alternative:
View Solutionसिद्ध कीजिए कि `|vecA xx vecB|^(2) + |vecA * vecB|^(2) = (AB)^(2).`
View SolutionIf `vecA` and `vecB` are two vectors, then which of the following is wrong?
View SolutionIf vector A and B have an angle `theta` between them, then value of `|hatA -hatB|` will be
View SolutionIf the angle between the vectors `vecA and vecB` is `theta,` the value of the product `(vecB xx vecA) * vecA` is equal to
View SolutionThe projection of the vector `vecA = hati - 2hatj + hatk` on the vector `vecB = 4hati - 4hatj + 7hatk` is
View SolutionThe area of the triangle formed by the adjacent sides with `vecA = 3hati + 2hatj - 4 hatk and vecB = -hati + 2hatj + hatk` is
View SolutionA Body moves 6m north, 8m east and 10m vertically upwards, what is its resultant displacement from initial position
View SolutionA man can swim with a speed 4km/hr in still water.
(a) How long does he takes to cross a river 1 km wide if the river flows steadily at 3 km/hr and makes his strokes normal to the river current?
(b) How far down the river does he go when he go when he reaches the other bank?
View SolutionAn aircraft is flying at a height of 3400 m above the ground. If the angle subtended at a ground observation point by the aircraft positions 10 s apart is `30^(@)` , what is the speed of the aircraft ?
View SolutionA fighter plane flying horizontally at an altitude of ` 1.5 km` with speed ` 720 kmh^(-1)` passes directly over head an anticraft gun.
At what angle from the vertical should the gun be fired from the shell with muzzle speed ` 600 ms^(-1)` to hit plane.
At what minimum altitude should the pilot fly the plane to avoid being hit ? ( Take g= 10 `ms^(-2)`).
View SolutionFrom a building two balls `A` and `B` are thrown such that `A` is thrown upwards and `B` downwards ( both vertically with the same speed ). If `v_(A) and v_(B)` are their respective velocities on reaching the ground , then
View Solution
MCQs questions and complete solutions for chapter MOTION IN A PLANE of MTG PHYSICS (ENGLISH) of Class 11
All Exercises from NCERT FINGERTIPS Class 11 PHYSICS MOTION IN A PLANE
- Addition And Subtraction Of Vectors - Graphical Method
- ASSERTION & REASON
- Assertion And Reason
- EXEMPLER PROBLEMS
- Higher Order Thinking Skills
- HOTS
- MCQs
- Miscellaneous Questions
- Motion In A Plane
- Motion In A Plane With A Constant Acceleration
- NCERT Exemplar
- Projectile Motion
- Relative Velocity In Two Dimensions
- Resolution Of Vectors
- Scalars And Vectors
- Uniform Circular Motion
- Vector Addition - Analytical Method