A ball is thrown from the top of a tower with an initial velocity of 10m/s at an angle of 30∘above the horizontal. It hits the ground at a distance of 17.3 m from the base of the tower. The height of the tower (g=10m/s2) will be
5 m
20 m
15 m
10 m
The correct Answer is:D
To solve the problem step by step, we will break down the motion of the ball into its horizontal and vertical components and use the equations of motion.
Step 1: Identify the given values
- Initial velocity, u=10m/s
- Angle of projection, θ=30∘
- Horizontal distance from the base of the tower, R=17.3m
- Acceleration due to gravity, g=10m/s2
Step 2: Calculate the horizontal and vertical components of the initial velocity
- The horizontal component of the velocity, ux=ucosθ
ux=10cos(30∘)=10×√32=10×0.866≈8.66m/s
- The vertical component of the velocity, uy=usinθ
uy=10sin(30∘)=10×12=5m/s
Step 3: Calculate the time of flight using horizontal motion
The horizontal distance traveled is given by:
R=ux⋅t
Rearranging for time t:
t=Rux=17.38.66≈2s
Step 4: Calculate the vertical displacement using vertical motion
Using the vertical motion equation:
h=uy⋅t−12gt2
Substituting the known values:
h=5⋅2−12⋅10⋅(22)
Calculating each term:
h=10−12⋅10⋅4=10−20=−10m
Step 5: Interpret the result
The negative sign indicates that the ball has fallen 10 meters below the point of projection, which means the height of the tower is:
Height of the tower=10m
Final Answer
The height of the tower is 10m.
---
- Initial velocity, u=10m/s
- Angle of projection, θ=30∘
- Horizontal distance from the base of the tower, R=17.3m
- Acceleration due to gravity, g=10m/s2
- The horizontal component of the velocity, ux=ucosθ
ux=10cos(30∘)=10×√32=10×0.866≈8.66m/s
uy=10sin(30∘)=10×12=5m/s
The horizontal distance traveled is given by:
R=ux⋅t
Rearranging for time t:
t=Rux=17.38.66≈2s
Using the vertical motion equation:
h=uy⋅t−12gt2
Substituting the known values:
h=5⋅2−12⋅10⋅(22)
Calculating each term:
h=10−12⋅10⋅4=10−20=−10m
The negative sign indicates that the ball has fallen 10 meters below the point of projection, which means the height of the tower is:
Height of the tower=10m
The height of the tower is 10m.
Topper's Solved these Questions
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - HOTS
6 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - EXEMPLER PROBLEMS
9 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assertion And Reason
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NCERT Exemplar
6 Videos
Similar Questions
A ball is thrown from the top of a tower with an intial velocity of 10 m//s at an angle 37∘ above the horizontal, hits the ground at a distance 16 m from the base of tower. Calculate height of tower. [g=10m/s2]
View SolutionA ball is thrown from the top of 36m high tower with velocity 5m/ss at an angle 37∘ above the horizontal as shown. Its horizontal distance on the ground is closest to [g=10m/s2
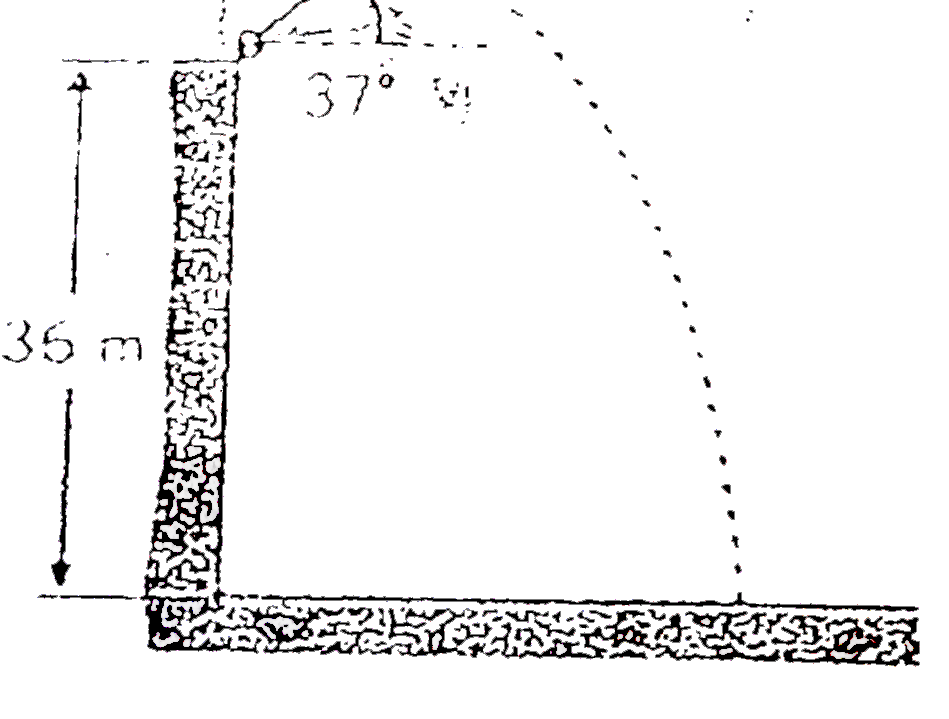 :
:
View SolutionA ball is throw from the top of a tower of 61 m high with a velocity 24.4ms−1 at an elevation of 30∘ above the horizon. What is the distance from the foot of the tower to the point where the ball hits the ground ?
View SolutionA stone is thrown from the top of a tower at an angle of 30∘ above the horizontal level with a velocity of 40 m/s. it strikes the ground after 5 second from the time of projection then the height of the tower is
View SolutionA ball is thrown upwards from the top of a tower 40m high with a velocity of 10m/s. Find the time when it strikes the ground. Take g=10m/s2.
View SolutionA ball is thrown upwards from the top of a tower 40m high with a velocity of 10m/s. Find the time when it strikes the ground. Take g=10m/s2.
View SolutionA ball is thrown from the top of a 35m high tower with initial velocity of magnitude u=80 ms−1 at an angle 25∘ with horizontal.
Find the time to reach the ground and the horizontal distance covered by the ball.
View SolutionA ball is thrown from the top of a 35m high tower with initial velocity of magnitude u=80 ms−1 at an angle 25∘ with horizontal.
Find the time to reach the ground and the horizontal distance covered by the ball.
View SolutionA pebbel is thrown horizantally from the top of a 20 m high tower with an initial velocity of 10m/s.The air drag is negligible . The speed of the peble when it is at the same distance from top as well as base of the tower (g=10m/s2)
View SolutionA ball is thrown vertically upwards from the top of a tower with an initial velocity of 19.6 ms−1 . The ball reaches the ground after 5s. Calculate the height of the tower .
View Solution
