Complete Solutions to Solved Examples of chapter MECHANICAL PROPERTIES OF FLUIDS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MECHANICAL PROPERTIES OF FLUIDS |
| MODERN PUBLICATION | Solved Examples |
| Number Of Questions | 61 |
| Academic Year | 2023-24 |
A drawing pin with a tip area of 0.1 mm`""^(2)` is pushed against a board with a force of 30 N. Calculate the pressure exerted at the tip.
View SolutionThe two thigh bones (femur bones) each of cross-sectional area `10 cm^(2)` support the upper part of a human body of mass 40 kg . Estimate the average pressure sustained by the femurs. `g=10m//s^(2)`
View SolutionThe area of the smaller piston of a hydraulic press is `1 cm^(2)` and that of larger piston is `22 cm^(2)`. How much weight can be raised on the larger piston by a `200 kg` f exerted on the smaller piston?
View SolutionTwo syringes of different cross-sections (without needles) filled with water are connected with a tightly fitted rubber tube filled with water. Diameters of the smaller piston and larger piston are 1.0cm and 3.0 cm respectively.
(a) Find the force on the larger piston when a force of 10N is applied to the smaller piston.
(b) The smaller piston is paused in through 6.0 cm, much does the larger piston move out?
View SolutionThe diameter of smaller piston of a hydraulic press is 3 cm that of a larger piston is 20cm. If a weight of 50 kg f is placed on the smaller piston, what will be the force exerted by the larger piston? If the stroke of smaller piston is 5cm, calculate the distance through which the larger will move after 6 strokes?
View SolutionCalculate the length of mercury column in a barometer tube which is inclined at an angle of `45^(@)` with horizontal direction if the atmospheric pressure is 75 cm of mercury.
View SolutionWhat is the pressure on a swimmer 10m below the surface of lake? `g=10ms^(-2)`, atmospheric pressure = `1.01 xx 10^(5)Pa`
View SolutionThe length breadth and height of a reactangle tank are 8m, 6m and 2m respectively. It is filled to the rim with a liquid of density of `2 xx 10^(3) kg//m^(3)`. Calculate the thrust exerted by the liquid at the bottom and walls of the tank. Take `g=9.8 m//s^(2)`
View SolutionA cylindrical tube of cross sectional area `20cm^(2)` is filled with water to a height of 10cm. The tube carries a tight fitting piston of negligible mass. What will be the pressure exerted at the bottom of the tube when a mass of 2 kg placed on the piston? Atmospheric pressure can be ignored.
View SolutionAt a depth of 1000 m in an ocean (a) what is the absolute pressure? (b) what is the gauge pressure? (c ) Find the force acting on the window of area `20 cm xx 20cm` of a submarine at this depth, the interior of which is maintained at sea-level atmospheric pressure. The density of sea water is `1.03 xx 10^(3) kg m^(-3)`, `g=10ms^(-2)`. Atmospheric pressure = `1.01 xx 10^(5) Pa`.
View SolutionA barometer is kept in an elevator accelerating upwards at `4.9 m//s^(2)`. If the barometer reads 77 cm of Hg, what will be the air pressure in the elevator?
View SolutionA body weights 5 kg in air. Calculate the apparent weight of the body in water if its density is `2000 kg//m^(3)`.
View SolutionA metal cube of mass 10 kg is floating in a liquid with `3/4` of its volume inside the liquid. Calculate:
(i) buoyant force acting on the cube.
(ii) ratio between density of cube and density of liquid.
Take `g=10 m//s^(2)`
View SolutionA ring of pure gold `(p=19.3 g//cm^(3))` is suspected to be hollow from inside. It weighs 40.350 g in air and 35.965 g in water. Calculate the volume of the hollow portion in gold, if any.
View SolutionA solid body is floating in water with 5/6th of its volume inside the water. What fraction of its volume will be outside if it ftoats in a liquid of specific gravity 1.6?
View SolutionA spring balance reads 10 kg when a bucket of water is suspended from it. What is the reading on the spring balance when (i) an ice cube of mass 1.5 kg is put into the bucket (ii) an iron piece of mass 7.8 kg suspended by another spring is immersed with half its volume inside the water n the bucket. Relative density of iron = 7.8
View SolutionA merchant claims to sell pure gold coins of relative density 19.3. He sells gold coins of weight 26.075 gf to a customer. In order to check the purity of gold coins, the customer weighs the coins when immersed in pure water and funds that they weigh 24.225 gf in, water. Was the merchant lying?
View SolutionA tank conatins iodine and water as shown in the adjoining figure. As aluminium cube of side 5cm is the equlibrium as shown. Calculate the fraction of volume of cube inside the iodine? Take
Relative density of iodine =4.927
Relative density of Aluminium =2.7
View SolutionA sample of milk consists of pure milk (density = 1080 kg/m`""^(3))` diluted with water `("density = 1000 kg/m"^(3))` and has a density of 1042 kg/m`""^(3).` Calculate the percentage of water by volume of milk.
View SolutionA circular metal plate of radius 4 cm rests on a layer of castor oil 2 mm thick, whose coefficient of viscosity is 16.5 `Nsm^(-2).` Calculate the horizontal force required to move the plate with a speed of 3 cm/s.
View SolutionA square metal plate of 5 cm side is moving parallel to another plate with a velocity of 10 cm/s. Both the plates are immersed in water. If the viscous force is 300 dyne and viscotity of water is 0.01 poise, then calculate the distance between the paltes.
View SolutionThe velocity of water near a river's surface is 20 km/hr. If the depth of the river is 4 m, calculate the shearing stress between the horizontal layers of water. Take, coefficient of viscosity of water = 0.01 poise.
View SolutionA metal block of area 0.10 `m^(2)` is connected to a 0.02 kg mass via a string. The string passes over an ideal pulley (considered massless and frictionless) as shown in figure. A liquid with a flim of thickness 0.15 mm is placed between the plate and the table. When released the plate movees to the right with a constant speed of 0.075 m `s^(-1)`. What is the coefficient of viscosity of the liquid?
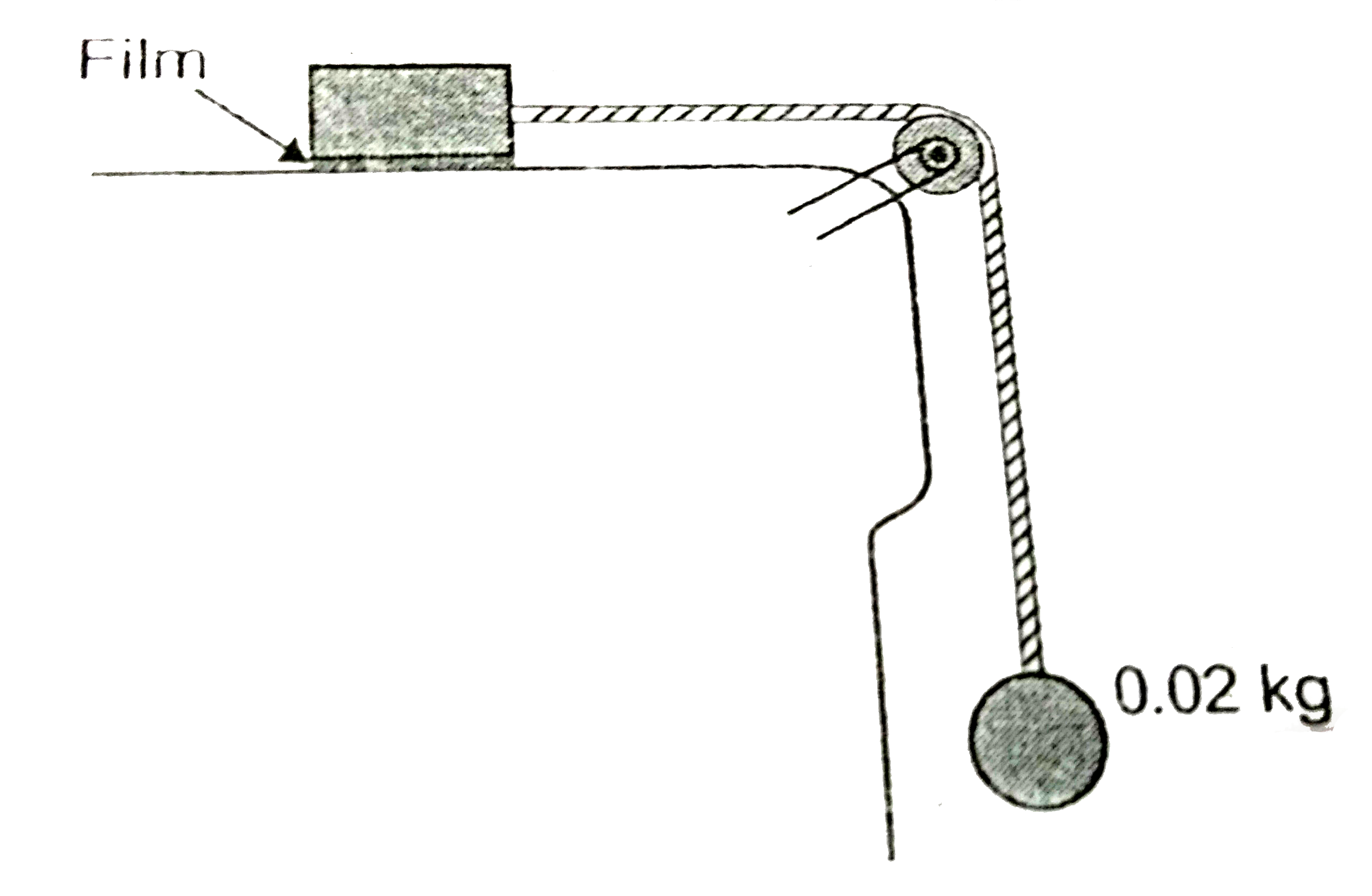
View SolutionA liquid flows through a horizontal pipe of varying cross section at a rate of 10 litres per minute. Find the velocity of liquid at a point where radius of pipe is 5 cm.
View SolutionWater is flowing at a speed of 0.5 m/s through a horizontal pipe of internal diameter 3 cm. Determine the diameter of the nozzle if the water is to emerge at a speed of 3 m/s.
View SolutionCalculate the speed at which the velocity of stream of water will be equal to 30 cm of mercury column.
View SolutionA pressure meter when attached with a closed horizontal pipe shows a reading of `5 xx 10^(5)" N/m"^(2).` When the valve of the pipe is opened, the reading of the pressure meter falls to `3.5 xx 10^(5) N//m^2.` Determine the speed of the water flowing in the pipe.
View SolutionA fully loaded Boeing aircraft has a mass of `3.3xx10^(5) kg`. Its total wing area is `500 m^(2)` . It is in level flight with a speed of `960 km//h`.
(a) Estimate the pressure difference between the lower and upper surfaces of the wings
(b) Estimate the fractional increases in the speed of the air on the upper surfaces of the wing relative to the lower surface. The density of air is `1.2 kg//m^(3)`.
View SolutionWhat is the minimum pressure required to force blood from the heart to the top of the heart (a vertical distance of 50 cm) ? Assume that the density of blood is `1.04 "gcm"^(-3)` and neglect friction.
View SolutionTwo horizontal pipes of different diameters are connected together and water is allowed to flow through them. The speed of water in the first pipe is 5 m/s and the pressure is `1.5 xx 10^4 N//m^2?` What will be the speed and pressure of water in the second pipe? The diameters of first and second pipes are 2 cm and 4 cm, respectively.
View SolutionA pitot tube is mounted in a main pipe of diameter 40 cm. If the difference in pressure indicated by the gauge ie 6cm of water column, calculate the volume of air passing through the main pipe in two minutes.
View SolutionCalculate the velocity with which water emerges from an orifice in a tank if the gauge pressure is `2 xx 10^5` N/m before the flow starts.
View SolutionA cylindrical drum of radius 20 cm has a capacity of `2.5 m^(3)` of water. It contains `1.8 m^(3)` of water and is placed on an iron block of same size as the drum. Calculate the horizontal range of water on the ground from an orifice made at lower end of drum, perepndicular to its length.
View SolutionThe diameter of a horizontal tube at points A and B are 6 cm and 3 cm, respectively. Two manometer limbs are attached at A and B. When water is allowed to flow through the tube, pressure difference of 10 cm is noted between the limbs. Calculate the rate of flow of water in the tube.
View SolutionThe following observations were made in an experiment with Poiseuille's apparatus:
Diameter of tube = 0.1 cm
Density of liquid=2.4 g/cm`""^(3)`
Volume of liquid collected per minute `= 10 cm^(3)`
Pressure head of liquid = 25 cm
Length of tube = 20 cm
Using the above data, calculate the viscosity of the liquid.
View SolutionA capillary tube of length 25 cm and diameter 0.1cm is fitted horizontally to a vessel full of a liquid of coefficient of visocity 0.012 cgs unit. The depth of the capillary tube below the surface of liquid is 15 cm. If the density of liquid is `0.8 g//cm^(3)`, calculate the amount of the liquid that will flow out in 7 minutes. Take `g=980 cm//s^(2)`
View SolutionWhile giving a patient a blood transfusion, a bottle is set up to pass the blood through a needle of length 2 cm and internal diameter 0.35 mm. If the level of blood is 1.4 m above needle, calculate the rate of flow and speed of the blood coming out of the needle. Take, coefficient of viscosity of blood =0.238 poise. Density of blood `=1020" kg/m"^(3)`.
View SolutionTwo tubes P and Q of lengths 100 cm and 30 cm have radii 0.1 mm and 0.2 mm, respectively. A liquid passing through the two tubes is entering P at a pressure of 60 cm of mercury-and leaving Q at a pressure of 55 cm of mercury. What is the pressure at the junction of Pand Q?
View SolutionTwo capillary tubes AB and BC are joined end to end at B, AB is 16cm long and of diameter 4mm whereas BC is 4cm long and of diameter 2mm. The composite tube is held horizontally with A connected to a vessel of water giving a constant head of 3cm and C is open to the air. Calculate the pressure difference between B and C.
View SolutionA cylindrical vessel has three identical horizontal tubes of length 40 cm, each coming out at heights 0, 5 and 9 cm, respectively. What will be the length of a single overflow tube of the same radius as that of identical tubes which can replace the three tubes if placed at the bottom of the vessel if the level of liquid in the cylindrical vessel is kept constant at 20 cm.
View SolutionA rain drop of radius 0.3 mm falls through air with a terminal viscosity of `1 m s^(-1)`. The viscosity of air is `18 xx 10^(-5)` poise. The viscous force on the rain drop is
View SolutionA gas bubble of radius 1 cm rises at a constant rate of 3 mm/s through a solution of density 4.16 g/cm`""^(3).` Determine the coefficient of viscosity of the solution. Neglect the density of the gas.
View SolutionAn iron ball of radius 0.2 cm and density 7.8 g/cm`""^(3)` falls through a tank of oil of density `=1.5 xx 10^(3)" kg/m"^(3)` and viscosity 9.92 poise.
What will the terminal velocity of the iron ball in the oil? Also, determine its terminal velocity in water of viscosity `10^(-3)" Nsm"^(-2)`.
View Solution27 rain drops of radius 1 mm each are falling down with a terminal velocity of 4 cm/s. They then coalesce to form a bigger drop. Determine the radius of bigger drop.
View SolutionA sphere is dropped under gravity through a fluid of viscosity `eta`. Taking the average acceleration as half of the initial acceleration, show that the time to attain the terminal velocity is independent of the fluid density.
View SolutionThe following observations were made in an experiment noith Poiseuille's apparatus: Calculate the average velocity of water in a tube of radius 0.05 cm so that the flow is turbulent. Take, viscosity of water = 0.001 Pa s.
View SolutionThe flow rate of water from a tap of diameter 1.25 cm is `0.48 L//mi n`. The coefficient of viscosity of water is `10^(-3) Pa-s`. After sometime, the flow rate is increased to `3L//mi n`. Characterise the flow for both the flow rates.
View SolutionA rectangular frame of length 20 cm is dipped in a soap solution and then raised, forming a soup film on the frame. The pull required is 2.83 g wt more before the film breaks. Calculate the surface tension of the liquid.
View SolutionA soap bubble is blown from a radius of 1 cm to 2 cm. Calculate the work done in doing so, if the surface tension of the soap solution is 42 dyne/cm.
View SolutionA drop of liquid of surface tension `sigma` and diameter D breaks up into 8 tiny drops. Calculate the resulting change in energy.
View SolutionTwo soap bubbles of radii 2 cm and 5 cm coalesce under isothermal condition in vaccum, to form a bigger bubble. Find the radius of new bubble.
View SolutionA glass plate of length 8cm, breadth 3 cm and thickness 0.2cm weighs 15 g in air. What will the apparent weight of the plate if it is half immersed vertically in water its long side held hrizontal? Take, Surface tension of water =70 dyne/cm
View Solutionn small droplets of water, each of radius r, coalesce ot form a single drop of radius R. Find
(i) Velocity acquired by bigger drop if all the energy released is converted into kinetic energy.
(ii) Rise in temperature.
Take, surface tension of water `=sigma`
Mechanical equivalent of heat =Q
View SolutionCalculate the pressure inside a small air bubble of radius 0.2 mm located just below the surface of water. Take,
Surface tension of water `=7.2 xx 10^(-2) N//m`
Atmospheric pressure `=1.01 xx 10^(5) N//m^(2)`
View SolutionIf the excess pressure inside a soap bubble of radius 5 mm is balanced by a 1.5 mm column of oil of specific gravity 0.76, find the surface tension of the soap solution.
View SolutionA glass tube having 2 mm bore is dipped vertically into a vessel containing mercury such that its lower end is 8 cm below the mercury surface. Determine the gauge pressure of air in the tube to blow a hemispherical bubble at its lower end.
Take, density of mercury `=13.6 "g/cm"^(3)`
Surface tension of mercury = 36 dyne/cm
View SolutionThe lower end of a capillary tube of diameter 2.00 mm is dipped 8.00 cm below the surface of water in a beaker. What is the pressure required in the tube in order to blow a hemispherical bubble at its end in water? The surface tension of water at the temperature of the experiments is `7.30 xx 10^(-2) "N/m"`. 1 atmospheric pressure `=1.01 xx 10^(5) Pa` density of water `=7000" kg/m"^(3), g="9.80 ms"^(-2)`. Also calculate the excess pressure.
View SolutionA capillary tube of radius 0.5 mm is dipped in a vessel containing water. Calculate the height to which water will rise in the capillary tube. Take, surface tension of water `=7.4 xx 10^(-3)" N/m".`
View SolutionA liquid of specific gravity 0.8 rises up in a capillary tube up to a height of 10 cm, while mercury falls down by 4 cm in the same tube. If the angle of contact between surface of the tube and liquid is zero and it is `135^(@)` for mercury, calculate the ratio of surface tension of mercury and the liquid. Take, specific gravity of mercury `=13.6 cos 135^@=-0.71`
View SolutionThe radii of two capillary tubes A and B are in the ratio of 3:1. If water rises to a height of 3 cm in tube A, how much it will rise in tube B. If the tube A is inclined at an angle of `30^(@)` with the vertical, then what will the position of water in the tube.
View SolutionA U-tube is made of capillaries of bore 2 mm and 4mm, respectively. The tube is held vertically inverted with the open ends below the surface liquid in a beaker. Calculate the difference in the levels of the meniscus in the two limbs. Take.
Surface tension of liquid =48 dyne/cm density `=0.8 g cm^(-3)`
Angle of contact between liquid and glass `=0^(@)`
`g=980 cm//s^(2)`.
View Solution
Solved Examples questions and complete solutions for chapter MECHANICAL PROPERTIES OF FLUIDS of MODERN PUBLISHERS PHYSICS (HINGLISH) of Class 11
All Exercises from MODERN PUBLICATION Class 11 PHYSICS MECHANICAL PROPERTIES OF FLUIDS
- Chapter Practise Test
- Competition File (A. MCQ (Objectie Type Questions))
- Competition File (Assertion Reason Type Questions)
- Competition File (B. MCQ (AIPMT/NEET & Other State Boards For Medical Entrance))
- Competition File (C. MCQ With More Than One Correct Answers)
- Competition File (D. MCQ Based On A Given Passage/Comprehension)
- Competition File (Integers Type Questions)
- Competition File (JEE (Advanced) For IIT Entrance)
- Competition File (JEE (Main) & Other State Boards For Engineering Entrance)
- Competition File (Matching Type Questions )
- Conceptual Questions
- HOTS (Higher Order Thinking Skills) (Advanced Level))
- NCERT (Additional Exercises)
- NCERT (Exemplar Problems (Subjective Questions))
- NCERT (Short Answer Type Questions)
- NCERT (Textbook Exercises)
- NCERT File (Exemplar Problems (Objective Questions))
- NCERT File (MCQ)
- Practice Problems
- Problems
- Revision Exercise (Additional Questions)
- Revision Exercise (Fill in the Blanks)
- Revision Exercise (Long Answer Questions)
- Revision Exercise (Numerical Problems)
- Revision Exercise (Short Answer Questions)
- Revision Exercise (Very Short Answer Questions)
- Solved Examples