A tank conatins iodine and water as shown in the adjoining figure. As aluminium cube of side 5cm is the equlibrium as shown. Calculate the fraction of volume of cube inside the iodine? Take
Relative density of iodine =4.927
Relative density of Aluminium =2.7 
Let the cube be x m inside the iodine. Then, depth of cube in water =(0.05 -x)m
Using Archimedes. principle, buoyant force on cube due to iodine is
F1=(0.05)2×x4.927×103×9.8N
=120.71x
Buoyant force on cube due to water is
F2=(0.05)2×(0.05−x)×103×9.8N
=1.225 -24.5 x
When the cube is in equilibrium, F1+F2=Weight of aluminium cube
120.71x+1.225−24.5x=(0.05)3×2.7×103×9.8
⇒=96.21x=2.085
⇒x=0.022m=2.2cm
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Practice Problems
52 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Conceptual Questions
29 Videos
- MATHEMATICAL TOOLSBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)
12 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
Similar Questions
A tank contains water and mercury as shown in . An iron cube of edge 6cm is in equilibrium as shown. What is the fraction of cube inside the mercury ? Given density of iron =7.7×103kgm−3 and density of mercury =13.6×103kgm−3.
View SolutionA solid wooden cone has been supported by a string inside water as shown in the figure. The radius of the circular base of the cone is R and the volume of the cone is v. In equilibrium the base of the cone is at a depth H below the water surface. Density of wood is d(<ρ, density of water).

(a) Find tension in the string.
(b) Find the force applied by the water on the slant surface of the coone. take atmospheric pressure to be p0.
View Solution
Knowledge Check
A tank contains water and mercury as shown in figure. An iron cube of edge d=6 cm is in equilibrium as shown. (density of iron =7.8×103kg/m3, density of mercury =13.6×103kg/m3, density of water =103kgm3)(Neglect the atmospheric pressure)

Time period of small oscillations of block isA2π√dρFe(ρHg−ρW)gB2π√dρFe(ρHg+ρW)gC2π√dρFeρHggD2π√dρFeρwgA cylindrical object of cork of mass 15g and cross-sectional area A1=10cm2 floats in a pan of water as shown in the figure. An aluminum, cylinder of mass 25g and cross-sectional area A2=2cm2 is attached 4cm below the cork and slides through a watertight frictionless hole in the bottom of the pan. Take density of the cork, ρ=0.2g/cm3,ρaluminium=2.7g/cm3,g=10m/s2. Based on the above information, answer the following questions.
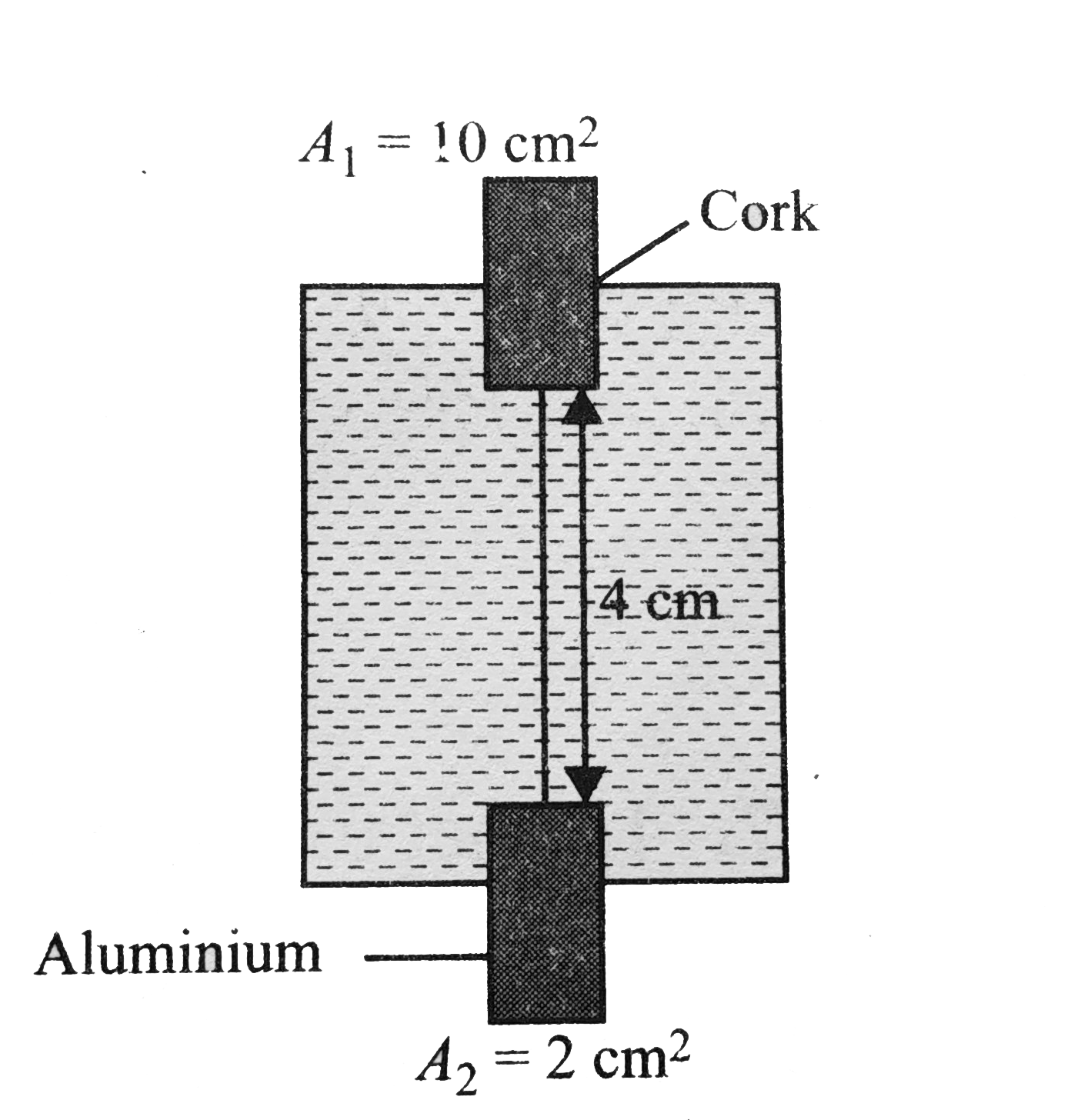
The tension in the string joining the cork and aluminium cylinder isA2NB1NC0.45ND0.6NA cylindrical object of cork of mass 15g and cross-sectional area A1=10cm2 floats in a pan of water as shown in the figure. An aluminum, cylinder of mass 25g and cross-sectional area A2=2cm2 is attached 4cm below the cork and slides through a watertight frictionless hole in the bottom of the pan. Take density of the cork, ρ=0.2g/cm3,ρaluminium=2.7g/cm3,g=10m/s2. Based on the above information, answer the following questions.

The length of the cork cylinder inside the water in equilibrium isA6cmB4cmC8cmD3cm
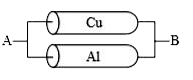
A Copper (Cu) rod of length 25 cm and cross sectional area 3mm2 is joined with a similar Aluminium (Al) rod as shown in figure. Find the resistance of the combination between the ends A and B.
(Take Resistivity of Copper =1.7×10–8Ωm Resistivity of Aluminium =2.6×10−8Ωm )
View SolutionA piece of aluminium of relative density 2.7 floats in mercury. Find the fraction of volume of aluminium piece which remains outside the mercury. The density of mercury is 13.6×103 kg/m3.
View SolutionA solid cube of sides 2 cm each is suspended by a thread and completely immersed in a liquid of density 0.85×103 kg/m3. What will be the tension in the thread if relative density of solid is 5?
View SolutionA metal cube of mass 10 kg is floating in a liquid with 34 of its volume inside the liquid. Calculate:
(i) buoyant force acting on the cube.
(ii) ratio between density of cube and density of liquid.
Take g=10m/s2
View SolutionA wooden block of mass 8kg is tied to a string attached to the bottom of a tank. The block is completely inside the water. Relative density of wood is 0.8. Taking g=10m/s2, What is the tension in the string ?
View Solution
