Complete Solutions to Competition File (JEE (Advanced) For IIT Entrance) of chapter MECHANICAL PROPERTIES OF FLUIDS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MECHANICAL PROPERTIES OF FLUIDS |
| MODERN PUBLICATION | Competition File (JEE (Advanced) For IIT Entrance) |
| Number Of Questions | 14 |
| Academic Year | 2023-24 |
When liquid medicine of density `rho` is to put in the eye, it is done with the help of a dropper. As the bulp on the top of the dropper is pressed, a drop forms at the opening of the dropper. We wish to estimate the size of the drop. We first assume that the drop formed at the opening is spherical because that requires a minimum increase in its surface energy. To determine the size, we calculate the net vertical force due to the surface tension T when the radius of the drop is R. When this force becomes smaller than the weight of the drop, the drop gets detached from the dropper.
If the radius of the opening of the dropper is r, the vertical force due to the surface tension on the drop of radius R (assuming r ltltR) is
View SolutionWhen liquid medicine of density `rho` is to be put in the eye, it is done with the help of a dropper. As the bylb on the top of the dropper is pressed. A drop frons at the opening of the dropper. We wish to estimate the size of the drop.
We first assume that the drop formed at the opening is spherical because that requires a minimum increase in its surface energy, To determine the size. We calculate the net vertical force due to the surface tension T when the radius of the drop is R. when this force become smaller than the weight of the drop the drop gets detached from the dropper.
If `r=5xx10^(-4)m,rho=10^(3) kg m^(-3), g=10ms^(-2), T=0.11Nm^(-1),` The radius of the drop when it detaches from the dropper is approximately,
View SolutionWhen liquid medicine of density `rho` is to be put in the eye, it is done with the help of a dropper. As the bylb on the top of the dropper is pressed. A drop frons at the opening of the dropper. We wish to estimate the size of the drop.
We first assume that the drop formed at the opening is spherical because that requires a minimum increase in its surface energy, To determine the size. We calculate the net vertical force due to the surface tension T=0.11 when the radius of the drop is R=1.4mm. when this force become smaller than the weight of the drop the drop gets detached from the dropper.
After the drop detaches, its surface energy is
View SolutionWater is filled in a container upto height 3m. A small hole of area 'a' is punched in the wall of the container at a height 52.5 cm from the bottom. The cross sectional area of the container is A. If `a//A=0.1` then `v^2` is (where v is the velocity of water coming out of the hole)
View SolutionWater is filled up to a height `h` in a beaker of radiys `R` as shown in the figure. The density of water is `rho`, the surface tension of water is `T ` and the atmospheric pressure is `P_(0)`. Consider a vertical section `ABCD` of the water column through a diameter of the beaker. The force on water on one side on this section by water on the other side of this section has magnitude

View SolutionTwo soap bubbles `A` and `B` are kept in a closed chamber where the air is maintained at pressure `8 N//m^(2)`. The radii of bubbles `A` and `B` are `2 cm` and `4 cm`, respectively. Surface tension of the soap. Water used to make bubbles is `0.04 N//m`. Find the ratio `n_(B)//n_(A)`, where `n_(A)` and `n_(B)` are the number of moles of air in bubbles `A` and `B` respectively. [Neglect the effect of gravity.]
View SolutionA cylindrical vessel of height 500mm has an orifice (small hole) at its bottom. The orifice is initially closed and water is filled in it up to height H. Now the top is completely sealed with a cap and the orifice at the bottom is opened. Some water comes out from the orifice and the water level in the vessel becomes steady with height of water column being 200mm. Find the fall in height(in mm) of water level due to opening of the orifice.
[Take atmospheric pressure `=1.0xx10^5N//m^2`, density of water=1000kg//m^3` and `g=10m//s^2`. Neglect any effect of surface tension.]
View SolutionA glass tube of uniform internal radius `(r)` has a valve separating the two identical ends. Initially, the valve is in a tightly closed position. End `1` has a hemispherical soap bubble of radius `r`. End `2` has sub-hemispherical soap bubble as shown in figure. Just after opening the valve.

View SolutionA spherical solid ball of volume V is made of a material of density `rho_1`. It is falling through a liquid of density `rho_2(rho_2ltrho_1)`. Assume that the liquid applies a viscous force on the ball that is proportional to the square of its speed v, i.e., `F_(viscous)=-kv^2(kgt0)`. The terminal speed of the ball is
View Solution
A jar filled with two non-mixing liquid 1 and 2 having densities `rho_(1)` and `rho_(2)` respectively. A solid ball, made of a material of density `rho_(3)` is dropped in the jar. It come to equilibrium in the position shown in the figure. Which of the following is true for `rho_(1),rho_(2)` and `rho_(3)`?
View SolutionA capillary tube (A) is dipped in water. Another identical tube (B) is dipped in a soap-water solution. Which of the following shows the relative nature of the liquid columns in the two tubes?
View SolutionThe pressure of a medium is charged from `1.01 xx 10. Pa` to `1.165 xx 10. Pa` and change in volume is 10 % keeping temperature constant. The Bulk modulus of the medium is
View SolutionConsider the spring-mass system, with the mass submerged in water, as shown in the figure. The phase space diagram for one cycle of this system is:

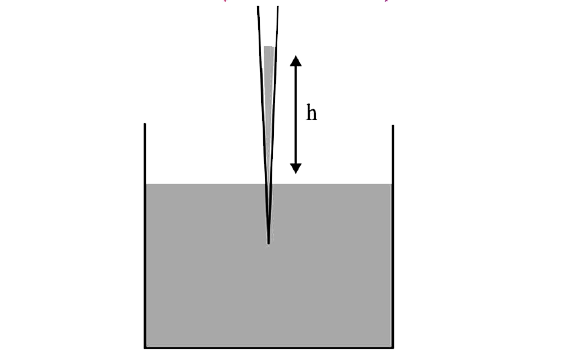
View SolutionA glass capillary tube is of the shape of a truncated cone with an apex angle `alpha` so that its two ends have cross sections of different radii. When dipped in water vertically, water rises in it to a high h, where the radius of its cross section is b. If the surface tension of water is S, its density if `rho`, and its contact angle with glass is `theta`, the value of h will be (g is the acceleration due to gravity)
View Solution
Competition File (JEE (Advanced) For IIT Entrance) questions and complete solutions for chapter MECHANICAL PROPERTIES OF FLUIDS of MODERN PUBLISHERS PHYSICS (HINGLISH) of Class 11
All Exercises from MODERN PUBLICATION Class 11 PHYSICS MECHANICAL PROPERTIES OF FLUIDS
- Chapter Practise Test
- Competition File (A. MCQ (Objectie Type Questions))
- Competition File (Assertion Reason Type Questions)
- Competition File (B. MCQ (AIPMT/NEET & Other State Boards For Medical Entrance))
- Competition File (C. MCQ With More Than One Correct Answers)
- Competition File (D. MCQ Based On A Given Passage/Comprehension)
- Competition File (Integers Type Questions)
- Competition File (JEE (Advanced) For IIT Entrance)
- Competition File (JEE (Main) & Other State Boards For Engineering Entrance)
- Competition File (Matching Type Questions )
- Conceptual Questions
- HOTS (Higher Order Thinking Skills) (Advanced Level))
- NCERT (Additional Exercises)
- NCERT (Exemplar Problems (Subjective Questions))
- NCERT (Short Answer Type Questions)
- NCERT (Textbook Exercises)
- NCERT File (Exemplar Problems (Objective Questions))
- NCERT File (MCQ)
- Practice Problems
- Problems
- Revision Exercise (Additional Questions)
- Revision Exercise (Fill in the Blanks)
- Revision Exercise (Long Answer Questions)
- Revision Exercise (Numerical Problems)
- Revision Exercise (Short Answer Questions)
- Revision Exercise (Very Short Answer Questions)
- Solved Examples