Complete Solutions to EXERCISE I of chapter OSCILLATIONS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS |
| AAKASH SERIES | EXERCISE I |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
A praticle moves in a circular path with a uniform speed. Its motion is
View SolutionWhich of the following is a necessary and sufficient condition for simple harmonic motion
View SolutionA particle is fastened at the end of a string and is whirled in a vertical circle with the other end of the string being fixed. The motion of the particle is
View SolutionIn S.H.M, there is always a constant ratio between the displacement of the body and its
View Solution(A) : All oscillatory motions are necessarily periodic motion in conservative fields but all periodic motion are not oscillatory.
(R) : Simple pendulum is an example of oscillatory motion.
View SolutionA student says that he had applied a force` F= - k/x `on a particle and the particle moved in simple harmonic motion. He refuses to tell whether k is a constant or not. Assume that he was worked only with positive x and no other force acted on the particle
View SolutionThe time period of a particle in simple harmonic motion is equal to the time between consecutive appearances of the particle at a particular point in its motion. This point is
View SolutionWhich of the following expression does not represent SHM
View SolutionA particle moves on the x-axis according to the equation `x=x_(0) sin 2wt`. The motion is simple harmonic.
View SolutionFor a particle executing simple harmonic motion, the acceleration is proportional to
View SolutionA particle moves on the x-axis according to the equation `x=A+B sin wt`. The motion is harmonic with amplitude
View SolutionThe motion of a particle is given by `X=Asinomegat+B cos omegat` the motion of the particle is
View SolutionThe linear superpositions of two simple harmonic motions of amplitudes A and B is
View SolutionA particle moves in the x-y plane according to the equation, `vecr=(hati+hatj)(A sin omegat+B cos omegat)`.
Motion of the particle is :
View SolutionAt two particular closest instants of time `t_(1)` and `t_(2)`, the displacements of a particle performing SHM are equal. At these instants.
View SolutionTwo linear simple harmonic motions of equal amplitude and frequancy are imposed on a particle along x and y axis respectively. The initial phase difference between them is `(pi)/2`.The resultant path followed by the particle is:
View SolutionThe function `(sin^(2) omegat)` represents
View SolutionThe motion of a torsional pendulum is
View SolutionRepresents two simple harmonic motions.
 the parameter which has different values in the two motions is
the parameter which has different values in the two motions is
View SolutionThe displacement of particle is represented by the equation `y=3cos((pi)/4-2omegat)`. The motion of the particle is
View SolutionThe displacement of particle is represented by the equation `y=sin^(3)omegat`. The motion is
View SolutionA particle is acted simultaneously by mutually perpendicular simple harmonic motion `x=a cos omegat` and `y=a sin omegat` the trajectory of motion of the particle will be
View SolutionWhich of the following statements is/are true for a simple harmonic oscillator?
View SolutionThe average acceleration in one time period in a simple harmonic motion is
View SolutionThe displacement of a particle in S.H.M is in opposite phase with
View SolutionAt the equilibrium position of a particle executing S.H.M
View SolutionFor a particle executing S.H.M along x-axis force is given by
View SolutionThe graph plotted between force and displacement of a particle executing S.H.M is
View SolutionA particle having SHM is located at different positions as shown below. The phase difference between the position marked by A and

View SolutionThe amplitude of a simple harmonic oscillator is doubled. Which of the following is also doubled?
View SolutionThe total mechanical energy of a spring-mass system in simple harmonic motion is `E= (1)/(2)m omegaA^(2)`. Suppose the oscillating particle is replaced by another particle of double the mass while the amplitude A remains the same, The new mechanical energy will
View Solution(A) : The graph of potential energy and kinetic energy of a particle in SHM with respect to position is a parabola.
(R) : Potential energy and kinetic energy do not vary linearly with position.
View SolutionWhen a body in SHM match the statements in column I with that in column II.

View SolutionWhen the amplitude of oscillation of a particle in S.H.M is increased to two times, the time period
View SolutionFor a particle executing S.H.M, which of the following statements is not correct ?
View SolutionChoose the correct statement.
a) Any motion that repeats itself in equal intervals of time along the same path is called periodic motion.
b) The displacement of a particle in periodic motion can always be expressed in terms of sine and cosine functions of time.
c) A body in periodic motion moves back and forth over the same path is called oscillatory or vibrating motion
d) Simple harmonic motion is a particular case of periodic motion.
View SolutionWhich of the following four statements is false ?
View SolutionIn a periodic motion when a body moves to and fro about a fixed mean position its acceleration.
View SolutionThe uniform circular motion in general can be described as a combination of two simple harmonic motions.
View SolutionFor a simple harmonic oscillator the frequency of oscillation is independent of
View SolutionThe phase difference between velocity and acceleration of simple harmonic oscillator.
View SolutionThe phase difference between acceleration and displacement of simple harmonic oscillator
View SolutionTotal energy of particle performing S.H.M. depends on
View SolutionThe work done by the body which is in S.H.M, against the restoring force is stored in the form of
View SolutionThe phase of simple harmonic motion at t = 0 is called
View SolutionA pendulum clock that keeps correct time on the earth is taken to the moon. It will run
View SolutionA wall clock uses a vertical spring mass system to measure the time. Each time the mass reaches an extreme position, the clock advances by a second. The clock gives correct time at the equator. If the clock is taken to the poles it will
View SolutionA pendulum clock keeping correct time tis taken to high altitude
View SolutionThe free end of a simple pendulum is attached to the ceiling of a box. The box is taken to a height and the pendulum is oscillated. When the bob is at its lowest point the box is released to fail freely. As seen from the box during this period, the bob will
View SolutionThe period of oscillation of a box suspended by a string of length 1 is `2pisqrt((l)/(g))` This expression is valid only for
View SolutionAn oscillating simple pendulum is arranged in a vacuum jar, then
View SolutionThe bob of a simple pendulum is hollow. Now its time period is T. If it is partially filled with water the time period will be
View SolutionPendulum clock shows correct time at `O^(@)C`. At a higher temperature the clock
View SolutionA seconds pendulum is taken from the surface of the earth to that of the moon. In order to maintain the period constant
View SolutionThe period of a simple pendulum suspended from the ceiling of a car is T when the car is at rest. If the car moves with a constant acceleration the period of the pendulum
View SolutionIf iron sphere is replaced by wooden sphere of same mass, time period of simple pendulum
View Solution(A) : The bob of a simple pendulum is a ball full of water. If a fine hole is made at the bottom of the ball, then the time period will no more remain constant.
(R): The time period of a simple pendulum does not depend upon mass.
View SolutionFor a simple pendulum graph between L and `T^(2)` will be a
View Solution(A): If a hole were drilled through the centre of earth and ball dropped into the hole at one end, it will oscillate.
(R): The ball will comes out of other end if passed through centre hole in earth.
View SolutionThe work done by the string of a simple pendulum in one complete oscillation is equal to
View SolutionThe bob of a simple pendulum of period T is given a negative charge. If it is allowed to oscillate with an identical charge at the point of suspension. The new time period will be
View SolutionA rubber ball filled with water, having a small hole is used as the bob of a simple pendulum. The period of such a pendulum
View SolutionIdentify the correct statement among the following
View SolutionThe restoring force which brings the bob towards the mean position is equal to
View SolutionTo show that a simple pendulum is in a simple harmonic motion it is necessary to assume that
View SolutionA simple body hanging freely and at rest is vertical because in that position.
View SolutionAn object is released from rest. The time it takes to final through a distance h and the speed of the object as it falls through this distance are measured with a pendulum clock.
The entire apparatus is taken on the moon and the experiment is repeated the measured times are same the measured speed are same the actual time in the fall are equal the actual speeds are equal moon and the experiment is repeated the measured times are same the measured speed are same the acrual time in the fall are equal the actual speeds are equal.
View Solution(A) : When a girl sitting on a swing stands up, the periodic time of the swing will decrease.
(R): In standing position of girl, the length of the swing will increase.
View SolutionA spring mass system oscillates with a frequency v, if is taken in an elevator slowly accelerating upward, the frequency will
View SolutionA bob is hung from an elastic spring to a support and set in motion in a vertical plane in a way similar to the oscillations of a simple pendulum. Its length will be maximum
View SolutionA clock 'S' is based on oscillations of a spring and a clock P is based on pendulum motion. Both clocks run at the same rate on earth on a planet having the same density as earth but twice the radius
View SolutionA spring of force constant K is cut into two parts whose lengths in the ratio 2 : 3. The part having larger force constant is
View Solution(A) : The spring constant of a spring is k. When it is divided into n equal parts, then spring constant of one piece is nk.
(B): The spring constant is independent of material used for the spring.
View SolutionThe time period of stiffer spring as compared to that of a soft spring is
View SolutionWhen a block is suspended by means of spring the restoring force per unit displacement of the block is called
View SolutionOne of the two clocks on earth is controlled by a pendulum and other by a spring. If both the clocks be taken to the moon, then which clock will show same time as that on earth
View SolutionThe time period of a loaded spring on earth is 6s. On the surface of moon, the time period of the same loaded spring will be
View Solution`T_(1)T_(2)` and `T_(3)` the time periods of a given pendulum on the surface of the earth, at a depth .h. in a mine and at an altitude .h. above the earth.s surface respectively, then
View SolutionIn case of forced vibration, the resonance wave becomes very sharp when the
View SolutionA particle with restoring force proportional to displacement and resisting force proportional to velocity is subjected to a force `Fsin omegat`. The amplitued of particle is maximum for frequency `omega=omega_(1)` while the energy is maximum for the frequency `omega = omega_(2)`, then (where `omega_(0)` = natural freqrency of oscillation of particle)
View SolutionA simple pendulum is set into vibrations. The bob of the pendulum comes to rest after some time due to
View SolutionIn damped oscillations, the amplitude of oscillation is reduced to one - third of its initial value `a_(0) ` at the end of 100 oscillations. When the oscillator completes 200 oscillations, the amplitude must be
View SolutionThe amplitude of vibration of a particle is given by `a_(m)=(a_(0))/(aw^(2)-bw+c)` where `a_(0)`, a , b and c are positive. The condition for a simple resonant frequency
View SolutionA body having natural frequency `v_(0) ` is executing forced oscillations under driving force of frequency v. The system will vibrate
View Solutionwhich of the following figure represents damped harmonic motion
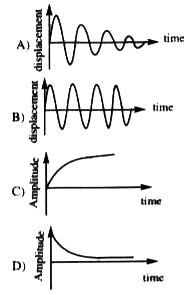
View SolutionA body executing forced oscillations under driving force is in sharp resonance. If damping increases then sharpness of resonance
View SolutionA particle of mass m is attached to a spring of spring constant .k. and has a natural frequency `omega_(0)`. An external force F(t) proportional to `cos omega t(omega != omega_(0))` is applied to the oscillator. The maximum displacement of the oscillator will be proportional to
View Solution(A) : Dampled oscillation indicates loss of energy.
(R) : The loss in damped oscillation may be due to friction, air resistance etc.
View SolutionIf amplitude of particle executing SHM is doubled, which of the following quantites are doubled
a.Time period
b. Maxomum velocity
c. Maximum acceleration
d. total energy
View SolutionIf the length of the simple pendulum is equal to the radius of the earth, anf it oscillates just above the surface of the earth then its time period is
a. `2pisqrt(R/(2g))`
b. `2pisqrt(R/g)`
c. nearly `59.5` minutes
d. `84.6` minutes
View SolutionIf a simple pendulum is arranged in an artificial satellite its
a. Time period becomes infinity
b.Frequency becomes infinity
c. Both time period and frequency become infinity
d.It does not oscillate
View Solution(A) : A wooden cube of side ' a' floats in a non viscous liquid of density 'p' When it is slightly pressed and released it executes SHM
(R ) :The net force responsible for SHM is the resultant of buoyancy force and true weight of the body.
View SolutionArrange the following simple pendulum in ascending order of their periods of oscillations
(a) of length 1m at a place of g = 8m/s
(b) of length 2m at a place of g = 10 m/s
(c) of length 4m at a place of g = 4m/s
View Solution(A) : The soldiers marching on a suspended bridge are advised to break their step.
(R) : Frequency of marching steps may match with the natural frequency of oscillations of bridge.
View SolutionWhich of the following pairs are correctly matched

View SolutionWhich of the following is a necessary and sufficient condition for simple harmonic motion
View SolutionA particle is fastened at the end of a string and is whirled in a vertical circle with the other end of the string being fixed. The motion of the particle is
View SolutionIn S.H.M, there is always a constant ratio between the displacement of the body and its
View SolutionAll oscillatory motions are necessarily periodic motion in conservative fields but all perodic motion are not oscillatory.
Simple pendulum is an example of oscillatory motion.
View SolutionA student says that he had applied a force` F= - r/x `on a particle and the particle moved in simple harmonic motion. He refuses to tell whether r is a constant or not. Assume that he was worked only with positive x and no other force acted on the particle
View Solution
EXERCISE I questions and complete solutions for chapter OSCILLATIONS of JEE (MAIN AND ADVANCED) PHYSICS of Class 11
All Exercises from AAKASH SERIES Class 11 PHYSICS OSCILLATIONS
- EXERCISE -1A
- EXERCISE -1A (Matching type questions)
- EXERCISE -I Equation of S.H.M
- EXERCISE -I Forced uscillations and resonance
- EXERCISE -I Simple pendulum
- EXERCISE -I Springs
- EXERCISE -I ASSERTION & REASON TYPE QUESTIONS
- EXERCISE -I Matching type questions
- EXERCISE -I MORE THAN ONE ANSWERS QUESTIONS
- EXERCISE -II Damping Motion
- EXERCISE -II Equations of SHM
- EXERCISE -II Simple pendulum
- EXERCISE -II SPRINGS
- EXERCISE I
- EXERCISE II
- EXERCISE-1B
- EXERCISE-2
- EXERCISE-3
- Practice exercise
- PRACTICE EXERCISE - EQUATIONS OF SHM
- PRACTICE EXERCISE - SIMPLE PENDULUM
- PRACTICE EXERCISE - SPRINGS
- PROBLEM