Complete Solutions to EXERCISE -I Equation of S.H.M of chapter OSCILLATIONS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS |
| AAKASH SERIES | EXERCISE -I Equation of S.H.M |
| Number Of Questions | 51 |
| Academic Year | 2023-24 |
Select the correct statements
View SolutionA particle moves in a circular path with a uniform speed. Its motion is
View SolutionA particle is fastened at the end of a string and is whirled in a vertical circle with the other end of the string being fixed. The motion of the particle is
View SolutionIn S.H.M, there is always a constant ratio between the displacement of the body and its
View SolutionWhich of the following is a necessary and sufficient condition for simple harmonic motion
View SolutionA student says that he had applied a force `F=- r//x` on a particle and the particle moved in simple harmonic motion. He refuses to tell whether r is a constant or not. Assume that he was worked only with positive x and no other force acted on the particle
View SolutionThe time period of a particle in simple harmonic motion is equal to the time between consecutive appearances of the particle at a particular point in its motion. This point is
View SolutionWhich of the following expression does not represent SHM
View SolutionA particle moves on the x-axis according to the equation `x = x_(0) sin 2omegat`. The motion is simple harmonic.
View SolutionFor a particle executing simple harmonic motion, the acceleration is proportional to
View SolutionA particle moves on the x-axis according to the equation x = A + B sinwt. The motion is harmonic with amplitude
View SolutionThe motion of a particle is given by `X = A sin omegat + Bcos omegat` the motion of the particle is
View SolutionThe linear superpositions of two simple harmonic motions of amplitudes A and B is
View SolutionA particle moves in the x-y plane according to the equation, `vecr = (hati+ hatj)(A sin omegat+ Bcos omegat)`. Motion of the particle is:
View SolutionAt two particular closest instants of time `t_(1)` and `t_(2)` the displacements of a particle performing SHM are equal. At these instants.
View SolutionTwo linear simple harmonic motions of equal amplitude and frequency are imposed on a particle along x and y axis respectively. The initial phase difference between them is `(pi)/(2)` The resultant path followed by the particle is:
View SolutionThe function `(sin^(2)omegat)` represents
View SolutionThe motion of a torsional pendulum is
View SolutionRepresents two simple harmonic motions.
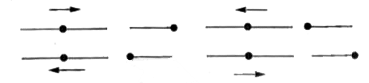
The parameter which has different values in the two motions is
View SolutionThe displacement of particle is represented by the equation `y=3cos((pi)/(4)-2omegat)`. The motion of the particle is
View SolutionThe displacement of particle is represented by the equation `y = sin^(3)omegat`. The motion is
View SolutionA particle is acted simultaneously by mutually perpendicular simple harmonic motion `x = a cos omegat` and `y = a sin omegat` The trajectory of motion of the particle will be
View SolutionWhich of the following statements `"is"//"are"` true for a simple harmonic oscillator ?
View SolutionThe average acceleration in one time period in a simple harmonic motion is
View SolutionThe ratio of maximum acceleration to maximum displacement of a Simple Harmonic Motion is equal to
View SolutionThe displacement of a particle in S.H.M is in opposite phase with
View SolutionAt the equilibrium position of a particle executing S.H.M
View SolutionFor a particle executing S.H.M along x-axis force is given by
View SolutionThe graph plotted between force and displacement of a particle executing S.H.M is
View SolutionA particle having SHM is located at different positions as shown below. The phase difference between the position marked by A and
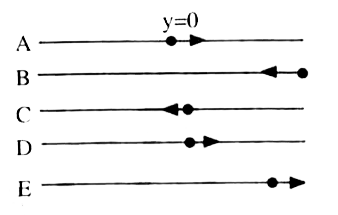
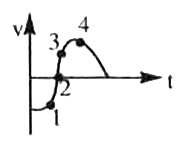
View SolutionVelocity - time graph of a particle executing SHM is as shown in fig. Select the correct alternatives.
A: at position 1, displacement of particle may be +ve or -ve
B: at position 2, displacement of particle is -ve
C: at position 3, acceleration of particle is +ve
D: at position 4, acceleration of particle is +ve
View SolutionThe amplitude of a simple harmonic oscillator is doubled. Which of the following is also doubled ?
View SolutionThe total mechanical energy of a spring-mass system in simple harmonic motion is `E= (1)/(2)m omegaA^(2)`. Suppose the oscillating particle is replaced by another particle of double the mass while the amplitude A remains the same, The new mechanical energy will
View SolutionIn simple harmonic motion, when the displacement is minimum then
View SolutionIn a simple harmonic motion
View SolutionWhen the amplitude of oscillation of a particle in S.H.M is increased to two times, the time period
View SolutionFor a body in Simple Harmonic Motion
View SolutionFor a particle executing S.H.M, which of the following statements is not correct ?
View SolutionChoose the correct statement.
a) Any motion that repeats itself in equal intervals of time along the same path is called periodic motion.
b) The displacement of a particle in periodic motion can always be expressed in terms of sine and cosine functions of time.
c) A body in periodic motion moves back and forth over the same path is called oscillatory or vibrating motion
d) Simple harmonic motion is a particular case of periodic motion.
View SolutionWhich of the following four statements is false ?
View SolutionIn a periodic motion when a body moves to and fro about a fixed mean position its acceleration.
View SolutionIn S.H.M.
View SolutionThe uniform circular motion in general can be described as a combination of two simple harmonic motions.
View SolutionStatement (a): The velocity of simple harmonic oscillator is maximum at mean position
Statement (b): At extreme position the acceleration of simple harmonic oscillator is maximum.
Statement (c): The velocity of simple harmonic oscillator is minimum at extreme position
View SolutionFor a simple harmonic oscillator the frequency of oscillation is independent of
View SolutionThe phase difference between velocity and acceleration of simple harmonic oscillator.
View SolutionThe phase difference between acceleration and displacement of simple harmonic oscillator
View SolutionStatement (a) During simple harmonic oscillation kinetic energy converted in potential energy and vice - versa
Statement (b): Total mechanical energy of simple harmonic oscillator is directly proportional to square of the frequency of oscillation
Statement (c): Simple harmonic oscillator obeys the law of conservation of energy.
Statement (d): Total mechanical energy of oscillator is directly proportional to a square of the amplitude of the oscillation
View SolutionTotal energy of particle performing S.H.M. depends on
View SolutionThe work done by the body which is in S.H.M, against the restoring force is stored in the form of
View SolutionThe phase of simple harmonic motion at t = 0 is called
View Solution
EXERCISE -I Equation of S.H.M questions and complete solutions for chapter OSCILLATIONS of JEE (MAIN AND ADVANCED) PHYSICS of Class 11
All Exercises from AAKASH SERIES Class 11 PHYSICS OSCILLATIONS
- EXERCISE -1A
- EXERCISE -1A (Matching type questions)
- EXERCISE -I Equation of S.H.M
- EXERCISE -I Forced uscillations and resonance
- EXERCISE -I Simple pendulum
- EXERCISE -I Springs
- EXERCISE -I ASSERTION & REASON TYPE QUESTIONS
- EXERCISE -I Matching type questions
- EXERCISE -I MORE THAN ONE ANSWERS QUESTIONS
- EXERCISE -II Damping Motion
- EXERCISE -II Equations of SHM
- EXERCISE -II Simple pendulum
- EXERCISE -II SPRINGS
- EXERCISE I
- EXERCISE II
- EXERCISE-1B
- EXERCISE-2
- EXERCISE-3
- Practice exercise
- PRACTICE EXERCISE - EQUATIONS OF SHM
- PRACTICE EXERCISE - SIMPLE PENDULUM
- PRACTICE EXERCISE - SPRINGS
- PROBLEM