Complete Solutions to EXERCISE -II Equations of SHM of chapter OSCILLATIONS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS |
| AAKASH SERIES | EXERCISE -II Equations of SHM |
| Number Of Questions | 38 |
| Academic Year | 2023-24 |
A particle is subjected to two S H Ms `x_(1) = A_(1) sin wt` and `x_(2) = A_(2)sin (wt + pi//4)`. The resultant SH M will have an amplitude of
View SolutionThe maximum displacement of an oscillating particle is 0.05m. If its time period is 1.57s (i) What is the velocity at the mean position ? (ii) What is its acceleration at the extreme position ?
View SolutionThe time period of a particle performing linear SHM is 12s. What is the time taken by it to make a displacement equal to half its amplitude ?
View SolutionThe amplitude and time period of a particle of mass 0.1 kg executing simple harmonic motion are 1m and 6.28s, respectively. Find its (i) angular frequency, (ii) acceleration and (iii) velocity at a displacement of 0.5m.
View SolutionThe frequency of a particle performing SHM is 12 Hz. Its amplitude is 4 cm. Its initial displacement is 2 cm towards positive extreme position. Its equation for displacement is
View SolutionThe equation motion of a particle in S.H.M is `a +16pi^(2)x = 0`. In the equation 'a' is the linear acceleration (in `m//"sec"`) of the particle at a displacement 'x' in meter. The time period of SHM in seconds is
View SolutionThe angular velocity and amplitude of a simple pendulum are 'w' and A respectively. At a displacement 'x'. If its KE is T' and PE is 'U' then the ratio of "T" to 'U' is
View SolutionWhich of the following expressions corresponds to simple harmonic motion along a straight line, where x is the displacement and a,b,c are positive constants ?
View SolutionTwo simple harmonic oscillators with amplitudes in the ratio 1: 2 are having the same total energy. The ratio of their frequencies is
View SolutionA particle is moving in a circle of radius R=1 m with constant speed `v=4m//s`. The ratio of the displacement to acceleration of the foot of the perpendicular drawn from the particle onto the diameter of the circle is
View SolutionA body dropped from a height h into the floor makes elastic collision with the floor. The frequency of oscillation of its periodic motion is
View SolutionA simple harmonic oscillator is of mass 0.1kg. It is oscillating with a frequency of `5//pi Hz`. If its amplitude of vibration is 5cm find the force acting on the particle at its extreme position
View SolutionThe displacement of a particle executing SHM is given by `Y = 10 sin (3t + pi//3 )`m and 't' is in seconds. The initial displacement and maximum velocity of the particle are respectively
View SolutionA particle is vibrating in SHM with an amplitude of 4cm. At what displacement from the equilibrium position it has half potential and half kinetic
View SolutionA particle moves according to the law `x = a cos(pit)/(2)`. The distance covered by it in the time 2 interval between t = 0 to t = 3 sec is
View SolutionIf a body of mass 36gm moves with S.H.M of amplitude A=13 cm and period T = 12sec. At a time t = 0 the displacement is x = +13cm. The shortest time of passage from x= +6.5cm to x = - 6.5 is
View SolutionFor a body in S.H.M the velocity is given by the relation `v= sqrt(144-16x^(2))m//"sec"`. The maximum acceleration is
View SolutionA 20g particle moves in SHM with a frequency of 3 oscillations per second and amplitude of 5 cm. Through what total distance does the particle move during one oscillation? What is its average speed
View SolutionAcceleration displacement graph of a particle executing S.H.M is as shown in given figure. The time period of its oscillation is (in sec)
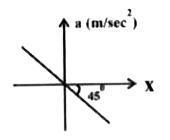
View SolutionThe displacement of particle from its mean position (in meter) is given by `Y = 0.2 sin( 10 pit+1.5 pi) cos (10 pit+1.5pi )`. The motion of the particle is
View SolutionTwo SHMs are represented by the equations
`y_(1)= 10sin(3pit+pi//4)` and `y_(2)= 5[sin3pit+ sqrt(3)cos3pit]` Their amplitudes are in ratio
View SolutionA Particle of mass 4 gm is moving simple harmonically with a period 8 sec and amplitude 8cm. What is its velocity when the displacement is 8cm
View SolutionWhich of the following quantities are always positive In a SHM
View SolutionFor a particle executing SHM. The KE 'K' is given by `K = K_(0) cos^(2) wt`. The maximum value of PE is
View SolutionA body executing SHM at a displacement 'x' its PE is `E_(1)` at a displacement 'Y' its PE is `E_(2)` The P.E at a displacement (x + y) is
View SolutionThe displacement of two identical particles executing SHM are represented by equations `x_(1)=4sin( 10t + (pi)/(2))` & `x_(2) = 5 cos(omegat)`. For what value of `omega`, energy of both the particles is same.
View SolutionA particle of mass m executes SHM with amplitude 'a' and frequency 'v'. The average kinetic energy during motion from the position of equilibrium to the end is:
View SolutionAn object is attached to the bottom of a light vertical spring and set vibrating. The maximum speed of the object is `15 "cm"// "sec"` and the period is 628 m sec. The amplitude of the motion in centimeter is
View SolutionAt what displacement is the KE of a particle performing SHM of amplitude 10 cm, three times its PE ?
View SolutionA particle execute S.H.M from the mean position. Its amplitude is A, its time period is 'T'. At what displacement, its speed is half of its maximum speed.
View SolutionAn object executing SHM has an acceleration of `0.2m//s^(2)` at a distance of 0.05m from the mean position. Calculate the period of SHM.
View SolutionThe angular velocities of three bodies in SHM are `w_(1), w_(2), w_(3)` with their respective amplitudes as `A_(1), A_(2), A_(3)`. If all three bodies have same mass and velocity then
View SolutionThe equation for the displacement of a particle executing SHM is `y = {5 sin 2pi t}` cm. Find (i) the velocity at 3cm from the mean position, (ii) acceleration after 0.5s after leaving the mean position
View SolutionThe velocity of a particle under going SHM at the mean position is `2ms^(-1)`. Find the velocity of the particle at the point where the displacement from the mean position is equal to half the amplitude.
View SolutionA block is placed on a horizontal platform. The system is making horizontal oscillations about a fixed point with a frequency of 0.5Hz. The maximum amplitude of oscillation if the block is not to slide on the horizontal platform, is (Coefficient of friction between the block and the platform = 0.4)
View SolutionA particle is subjected to two simple harmonic motions in the same direction having equal amplitudes and equal frequency. If the resulting amplitude is equal to the amplitude of individual motions, the phase difference between them is:
View SolutionIf the maximum acceleration of a S.H.M. is a and the maximum velocity is b then amplitude of vibration is given by
View SolutionA particle is executing simple harmonic motion with an amplitude A and time period T. The displacement of the particles after 2T period from its initial position is
View Solution
EXERCISE -II Equations of SHM questions and complete solutions for chapter OSCILLATIONS of JEE (MAIN AND ADVANCED) PHYSICS of Class 11
All Exercises from AAKASH SERIES Class 11 PHYSICS OSCILLATIONS
- EXERCISE -1A
- EXERCISE -1A (Matching type questions)
- EXERCISE -I Equation of S.H.M
- EXERCISE -I Forced uscillations and resonance
- EXERCISE -I Simple pendulum
- EXERCISE -I Springs
- EXERCISE -I ASSERTION & REASON TYPE QUESTIONS
- EXERCISE -I Matching type questions
- EXERCISE -I MORE THAN ONE ANSWERS QUESTIONS
- EXERCISE -II Damping Motion
- EXERCISE -II Equations of SHM
- EXERCISE -II Simple pendulum
- EXERCISE -II SPRINGS
- EXERCISE I
- EXERCISE II
- EXERCISE-1B
- EXERCISE-2
- EXERCISE-3
- Practice exercise
- PRACTICE EXERCISE - EQUATIONS OF SHM
- PRACTICE EXERCISE - SIMPLE PENDULUM
- PRACTICE EXERCISE - SPRINGS
- PROBLEM