Complete Solutions to Problems of chapter SYSTEM OF PARTICLES AND ROTATIONAL MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SYSTEM OF PARTICLES AND ROTATIONAL MOTION |
| AAKASH SERIES | Problems |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
If the distance between the centres of the atoms of potassium and bromine in KBr (potassium - bromide) molecule is `0.282xx10^(-9)`m, find the centre of mass of this particle system from potassium (mass of bromine = 80 u, and of potassium = 39 u).
View SolutionWhen .n. number of particles of masses m, 2m, 3m, …….. nm are at distances `x_(1)=1, x_(2)=2, x_(3)=3, ……………x_(n) =n` units respectively from origin on the x-axis, then find the distance of centre of mass of the system from origin.
View SolutionWhen `n` number of particles of masses `m, 2m, 3m, …….. nm` are at distances `x_(1)=1, x_(2)=4, x_(3)=9, ………x_(n)=n^(2)` units respectively from origin on the x-axis, then find the distance of their centre of mass from origin.
View SolutionWhen `n` number of particles each of mass `m` are at distances `x_(1)=a, x_(2)=ar, x_(3)=ar^(2)…….x_(n)=ar^(n)` units from origin on the x-axis, then the distance of their centre of mass from origin.
View SolutionWhen `n` number of particles each of mass `m` are at distances `x_(1)=1, x_(2)=2, x_(3)=3, ………., x_(n)=n` units from origin on the x-axis, then find the distance of their centre of mass from origin.
View SolutionTwo particles of masses 10 kg and 30 kg are lying on a straight line. The 10 kg mass is shifted towards the 30 kg mass by a distance of 2cm. By what distance should the 30kg mass be shifted so that the position of their centre of mass does not change
View SolutionA 1m long rod having a constant cross sectional area is made of four materials. The first `0.2m` are made of iron, the next `0.3m` of lead, the following `0.2m` of aluminium and the remaining part is made of copper. Find the centre of mass of the rod. The densities of iron, lead aluminium and copper are `7.9xx10^(3)kg//m^(3)`, `11.4xx10^(3)kg//m^(3)`, `2.7xx10^(3)kg//m^(3)` and `8.9xx10^(3)kg//m^(3)` respectively.
View SolutionFind the position of centre of mass of the system of 3 objects of masses 1 kg, 2kg and 3 kg located at the corner of an equilateral triangle of side 1 m. Take 1 kg mass object at the origin and 2kg along x-axis.
View SolutionFour particles of masses 1 kg, 2 kg, 3 kg and 4 kg are placed at the four vertices A, B, C and D of the square of side 1 m. Find the position of centre of mass of the particles.
View SolutionFind position of centre of mass of four particle system, which are at the vertices of a parallelogram, as shown in figure.
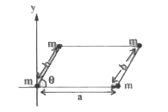
View SolutionIf the centre of mass of three particles of masses of 1kg, 2 kg, 3 kg is at (2, 2, 2), then where should a fourth particle of mass 4 kg be placed so that the combined centre of mass may be at (0, 0, 0).
View SolutionA system consists of three particles located at the corners of a right triangle as shown in the figure. Fin the position vector of centre of mass of the system.
View SolutionThe position vectors of three particles of mass `m_(1)=1kg, m_(2)=2kg` and `m_(3)=4` are `vec(r_(1))=(hat(i)+4hat(j)+hat(k))m, vec(r_(2))=(hat(i)+hat(j)+hat(k))m,` and `vec(r_(3))=(2hat(i)-hat(j)+2hat(k))m,` respectively. Find the position vector of their centre of mass.
View SolutionTwo `3kg` masses have velocities `barv_(1)=2hat(i)+3hat(j)m//s` and `barv_(2)=4hat(i)-6hat(j)m//s`. Find a) velocity of centre of mass, b) the total momentum of the system, C) The velocity of centre of mass `5`s after application of a constant force `bar(F)=24hat(i)N, d)` position of centre of mass after `5`s if it is at the origin at t=0
View SolutionFind the acceleration of center of mass of the blocks of masses `m_(1)` and `m_(2) (m_(1)gt m_(2))` in Atwood's machine :
View SolutionAn object A is dropped from rest the top of a `30m` high building and at the same moment another object B is projected vertically upwards with an initial speed of `15m//s` from the base of the building. Mass of the object A is `2kg` while mass of the object B is `4kg`. Find the maximum height above the ground level attained by the centre of mass of the A and B system (take `g=10m//s^(2))`
View SolutionTwo masses `m_(1)` and `m_(2)` are connected by a spring of force constant k and are placed on a frictionless horizontal surface. Initially the spring is stretched through a distance `x_(0)`, when the system is released from rest. Find the distance moved by two masses before they again comes to rest.
View SolutionA projectile is fired at a speed of `100m//s` at an angle of `37^(0)` above the horizontal. At the highest point the projectile breaks into two parts of mass ratio `1:3`, the smaller piece coming to rest. Find the distance from the launchind point to the point where the heavier piece lands.
View SolutionA ladder AP of length `5m` inclined to a vertical wall is slipping over a horizontal surface with velocity of `2m//s`, when A is at a distance `3m` from O, the velocity of CM at this moment is

View SolutionA uniform piece of metal sheet is cut in the form as shown in the fig. Locate the centre of mass of the piece.
View SolutionA uniform sheet of steel is cut into the shape as shown. Compute the X and Y co-ordinated of the centre of mass of the piece. (Width of each plate is `10cm` )
View SolutionIf the linear density of a rod of length L varies as `lambda=A+Bx`, find the position of its centre of mass.
View SolutionIf the linear density of a rod of length L varies as `lambda=(kx^(2))/(L)` where k is a constant and x is the distance of any point from one end, then find the distance of centre of mass from the end at `x=0`.
View SolutionIdentical blocks each of mass M and length L are placed one above the other such that each extends out by maximum length as shown in figure. Find the maximum extension of the `n^(th)` block from the top. So that the blocks will not fall.

View SolutionA car is moving in a circular path with a uniform speed v. Find the magnitude of change in its velocity when the car rotates through an angle `theta`.
View SolutionWhat is the linear velocity of a person at equator of the earth due to its spinning motion? (Radius of the earth = 6400 km.)
View SolutionWhen a force of 10.0 N is exerted on the handle of a door, the door can be just opened. If the handle is a distance of 50 cm from the hinges find the torque applied on the door.
View SolutionA roller of mass `300kg` rests against a step of height `20cm`. If the radius of the roller is `50cm` find the minimum horizontal force to be applied passing through its centre of mass to take the roller on the step.
View SolutionA particle is projected at time t-0 from a point 'O' with a speed 'v' at an angle `theta` to horizontal. Find the torque of gravitational force on projectile about the origin at time 't'. (xy plane is vertical plane)

View SolutionPQR is a rigid equilateral triangular frame of side length 'L'. Forces `F_(1), F_(2)` and `F_(3)` are acting along PQ, QR and PR. Find the relation between the forces if system is in equilibrium.
View SolutionA metre stick is balanced on a knife edge at its centre. When two coins, each of mass 5g are put one on top of the other at the 12.0 cm mark, the stick is found to be balanced at 45.0 cm. What is the mass of the metre stick?
View SolutionA uniform ladder of mass `10kg` leans against a smooth vertical wall making an angle `53^(0)` with it. The other end rests on a rough horizontal floor. Find the normal force and the frictional force that the floor exerts on the ladder.
View SolutionA boy and a man carry a uniform pole of length `8m` and of mass `60kg` by supporting it on their shoulders. They are located at the ends of the pole. Where should a load of `90kg` be suspended from boy's end so that boy carries only one-third of the total load ?
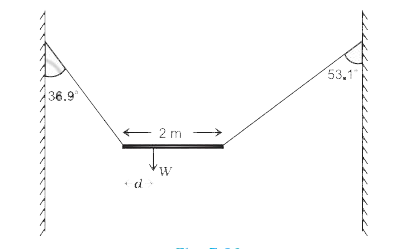
View SolutionA non-uniform bar of weight W is suspended at rest by two strings of negligible weight as shown in Fig.7.39. The angles made by the strings with the vertical are `36.9^(@)` and `53.1°` respectively. The bar is 2 m long. Calculate the distance d of the centre of gravity of the bar from its left end.
View SolutionThree particles of masses `1g, 2g`and `3g` are at distances of `1cm, 2cm` and `3cm` from the axis of rotation. Find i) the moment of inertia of the system and ii) the radius of gyration of the system.
View SolutionTwo objects of masses `1kg` and `2kg` separated by a distance of `1.2` m are rotating about their centre of mass. Find the moment of inertia of the system.
View SolutionA uniform rod of length l is held vertically on a horizontal floor fixing its lower end, the rod is allowed of fall onto the ground. Find (i) its angular velocity at that instant of reaching the ground (ii) The linear velocity with which the tip of rod falls to floor.
View SolutionWhat is the work done in increasing the angular frequency of a circular ring of mass `2kg` and radius `25cm` from `10` rpm to `20` rpm about ist axis ?
View SolutionA hoop of mass `500g` and radius `10cm` is placed on a nail. Find the moment of inertia of the hoop when it is rotated about the nail.
View SolutionThe angular frequency of a fan of moment of inertia `0.1kg m^(2)` is increased from `30` rpm to `60` rpm when a torque of `0.03` Nm acts on it. Find the number revolutions made by the fan while the angular frequency is increased from `30` rpm to `60` rpm.
View SolutionFind the moment of inertia of a thin uniform rod about an axis perpendicular to its length and passing through a point which is at a distance of `(l)/(3)` from one end. Also find radius of gyration about that axis.
View SolutionThe radius of gyration of a body about an axis at a distance of `12` cm from its centre of mass is `13` cm. Find its radius of gyration about a parallel axis through its centre of mass.
View SolutionA flywheel in the form of a disc is initially at rest. When a constant torque acts on it for one minute, it attains a speed of `600` rpm. Calculate the torque, if mass and radius of the disc are `10` kg and `0.4`m respectively.
View SolutionRadius of gyration of a disc of mass `5kg` about a transverse axis passing through its centre is `14.14cm`. Find its radius of gyration about its diameter and hence calculate its moment of inertia about its diameter
View SolutionFind the ratio of the moments of inertia to two solid spheres of same mass but densities in the ratio `1:8`.
View SolutionFrom a disc of mass 'm' and radius 'r'. A circular portion of radius `(r )/(3)` is removed from the edges. Find the M.I of the remaining system about a normal through centre of original disc
View SolutionA disc of mass m and radius R has a concentric hole of radius r. Find the M.I about a normal axis to its plane and passing through centre of disc.
View SolutionParticles of masses `1g, 2g, 3g,…. 100g` are kept at the marks `1cm, 2cm, 3cm,… 100cm` respectively on a meter scale. Find the moment of inertia of the system of particles about a perpendicular bisector of the meter scale.
View SolutionThree particles each of mass `100g` are placed at the vertices of an equilateral triangle of side length `10cm`. Find the moment of inertia of the system about an axis passing through the centroid of the triangle and perpendicular to its plane.
View SolutionFour particles each of mass `100g` are placed at the corners of a square of side `10cm`. Find the moment of inertia of the system about an axis passing through the centre of the square and perpendicular to its plane. Find also the radius of gyration of the system.
View SolutionThe radius of gyration of a body about an axis passing through its centre of mass is `24cm`. Calculate the radius of gyration of the body about a parallel axis passing through a point at a distance of `7cm` from its centre of mass.
View SolutionA bar magnet of length `5.0cm` and breadth `1.2` cm is rotated about an axis passing through its center and perpendicular to its plane. Find its moment of inertia if the mass of the magnet is `200g`.
View SolutionA thin square plate is of mass m and the length of each of its sides is l. Find the moment of inertia of the plate when it is rotating about an axis (i) passing through its centre and perpendicular to its plane and (ii) passing through one of its corners and perpendicular to its plane.
View SolutionFour thin uniform rods each of mass m and length l are arranged to form a square. Find the moment of inertia of the system about an axis (i) Passing through its centre and perpendicular to its plane. (ii) Passing through one of its sides. (iii) Passing through a corner and perpendicular to its plane. (iv) About a disgonal of the system.
View SolutionTwo circular rings of equal mass and radius are placed in such a way that their centres coincide but their planes are mutually perpendicular. Find the moment of inertia of the system when the system is rotated about the diameter of one of the rings.
View SolutionThe radius of gyration of a uniform disc about a line perpendicular to the disc is equal to its radius. Find the distance of the line from the centre of the disc.
View SolutionTwo uniform circular discs, each of mass `1kg` and radius `20cm`, are kept in contact about the tangent passing through the point of contact. Find the moment of inertia of the system about the tangent passing through the point of contact.
View SolutionThree uniform circular discs, each of mass `0.5kg` and radius `10cm`, are kept in contact with each other as shown in the figure. Find the moment of inertia of the system when it rotates about the axis AB.
View SolutionFour spheres each of diameter `2a` and mass m are placed with their centres on the four corners of a square of the side b. Calculate the moment of inertia of the system about and side of the square.
View SolutionA rod PQ of mass 'm' and length L is rotated about an axis through 'P' as shwon in figure. Find the moment of inertia of the rod about the axis of rotation.

View SolutionFrom a complete ring of mass M and radius R, an are of making `30^(0)` at centre is removed. What is the moment of inertia of the incomplete ring about an axis passing through the centre of the ring and `bot^(er)`to the plane of the ring
View SolutionFour holes of radius R are cut from a thin square plate of side 4R and mass M. Then moment of inertia of the remaining portion about z axis is
View SolutionThe motor of an engine is rotating about its axis with angular velocity of `120` r.p.m. it comes to rest in `10s`, after being switched off. Assuming constant deceleration, calculate the number of revolutions made by it before coming to rest.
View SolutionThe spin drier of a washing machine revolving at `15` r.p.s slows down to `5` r.p.s., while making `50` revolutions. Find (a) angular acceleration and (b) time taken.
View SolutionTwo particles, each of mass m and speed v, travel in opposite directions along parallel lines separated by a distance d. Show that the vector angular momentum of the two particle system is the same whatever be the point about which the angular momentum is taken.
View SolutionThe pulley of Atwood's machine has a moment of inertia 'I' about its axis and its radius is R. Find the magnitude of acceleration of the two blocks assuming the string is light and does not slip on the pulley.
View SolutionA massless string is wrapped around a disc that has a radius of `10cm` and mass of `1.500kg`. The free end of the string is attached to a hanging block of mass `1.000kg`, the other end is fixed to a point on the rim of the disk . Neglecting friction, find the linear acceleration of the hanging block if the block is released from rest. `(g=10ms^(-2))`

View SolutionA rigid body is made of three identical thin rods, each of length 'L' fastended together in the form of the letter 'H'. The body is free to rotate about a horizontal axis that runs along the length of one of the legs of 'H'. The body is allowed to fall from rest from a position in which the plane of 'H' is horizontal. What is the angular speed of the body when the plane of 'H' is vertical ?
View SolutionA solid cyclinder of mass M and radius 'R' is mounted on a frictionless horizontal axle so that it can freely rotate about this axis. A string of negligible mass is wrapped round the cylinder and a body of mass 'm' is hung from the string. The mass is released from rest. Find the tension in the string and the angular speed of cylinder as the mass falls a distance h
View SolutionA cylindrical rod of mass 'm' length L and radius 'R' has two cords wound around it whose ends are attached to a rigid support. The rod is held horozontally with the two cords vertical. When the rod is released, the cords unwind and rod rotates. Find the tension in the cords as they unwound and determine the linear acceleration of the cylinder as it falls.
View SolutionA uniform rod of mass m and length l is suspended by means of two light inextensible strings at the ends of rod. Tension in one string immediately after the other string is cut is
View SolutionThe angular momentum of a body changes by `80kg m^(2)s^(-1)` when its angular velocity changes from `20 rad s^(-1)` to `40 rad s^(-1)`. Find the change in its kinetic energy of rotation.
View SolutionIf the radius of the earth is suddenly halved keeping its mass constant find its time period of rotation around its own axis
View SolutionA horizontal disc is freely rotating about a vertical axis passing through its centre at the rate of `100` rpm. A bob of wax of mass `20g` falls on the disc and sticks to it a distance of `5cm` from the axis. If the moment of inertia of the disc about the given axis is `2xx10^(-4)kg m^(2)`, find new frequency of rotation of the disc.
View SolutionA ballet dancer spins about a vertical axis at `60` rpm with arms outstretched. When her arms folded the angular frequency increases to `90` rpm. Find the change in her moment of inertia.
View SolutionDetermine the kinetic energy of a circular disc rotating with a speed of `60` rpm about an axis passing through a point on its circumference and perpedicular to its plane. The circular disc has a mass of `5kg` and radius `1m`.
View SolutionThe angular momentum of rotating body is increased by `20%`. What will be the increase in its rotational kinetic energy ?
View SolutionA massless string is wrapped around a uniform solid cylinder of mass `30kg` and radius `0.20m`. One end of the string is attahed to the cylinder and the free end is pulled tangentially by a force that maintains a constant tension of `3.0` N. Find a) the angular acceleration and b) The angular speed of the cylinder `2.0` s after the force is applied to the cylinder at rest.
View SolutionA door of moment of inertia `4kgm^(2)` is at rest. When a torque of `2piNm^("acts")` on it find its angular acceleration. Find also its angular velocity after `1`s .
View SolutionA ballet dancer spins about a vertical axis at `120` rpm with arms outstretched. With her arms folded, the moment of inertia about the axis of rotation decreases by `4%`. Calculate the new rate of rotation.
View SolutionA wheel is rotating with a speed of `500` rpm on a shaft. Second identical wheel, initially at rest is suddenly coupled on the same shaft. What is the speed of the resultant combination ? Assume that the moment of inertia of the shaft is negligible.
View SolutionThe moment of inertia of a fly wheel making `300` revolutions per minute is `0.3kgm^(2)`, find torque required to bring it to rest in `20s`.
View SolutionA circular metal disc of mass `200g` and radius `20cm` makes `10` revolutions per second about an axis passing through the centre and perpendicular to its plane. Find a) Moment of inertia about to axis, b) Torque required to change its angular velocity from `10` rps to `20` rps in `5s`.
View SolutionWhen `100` J of work is done on a fly wheel, its angular velocity is increased from `60` rpm to `180` rpm. What is the moment of inertia of the wheel ?
View SolutionA metal piece of mass `120g` is stretched to form a plane rectangular sheet of area of cross section `0.54m^(2)`. If length and breadth of this sheet are in the ratio `1:6`, find its moment of inertia about an axis passing through its centre and perpendicular to its plane.
View SolutionA uniform rod AB of mass 'm' length `2a` is allowed to fall under gravity with AB in horizontal. When the speed of the rod is 'v', suddenly the end 'A' is fixed. Find the angular velocity with which it begins to rotate .
View SolutionA uniform rod of mass 'm' and length 'l' is on the smooth horizontal surface. When a constant force 'F' is applied at one end of the rod for a small time 't' as shown in the figure. Find the angular velocity of the rod about this centre of mass.

View SolutionA uniform bar of length 6a and mass 8m lies on a smooth horizontal table. Two point masses m and 2m moving in the same horizontal plane with speeds 2v and v respectively, strike the bar (as show in fig) and stick to the bar after collision. Calculate (a) velocity of the centre of mass (b) angular velocity about centre of mass and (c ) total kientic energy, jsut after collosion.

View SolutionA particle is projected at time t=0 from a point 'O' with a speed 'u' at an angle `45^(0)` to horizontal. Find the angular momentum of particle at time `t=u//g`.

View SolutionA circular platform is mounted on a vertical frictionless axle. Its radius is `r=2m` and its moment of inertia is `I=200kg-m^(2)`. It is initially at rest. A `70kg` man stands on the edge of the platform and begins to walk along the edge at speed `V_(0)=1.0` m/s relative to the ground. Find the angular velocity of the platform.
View SolutionA uniform cylinder of height h and radius r is placed with its circular face on a rough inclined plane and the inclination of the plane to the horizontal gradually in creased. If `mu` is the coefficeint of friction, then under what conditions the cylinder will
a) slide before topping
b) topple before sliding
View SolutionA uniform cube of side a and mass m rests on a rough horizontal table. A horizontal face F is applied normal to one of the face at a point directly above the centre of the face, at a height `(3a)/(4)` above the base. What is the minimum value of F for which the cube begins to topple about an edge ?
View SolutionA force F is applied on the top of a cube as shown in figure. The coefficient of friction between the cube and the ground is `mu`. If F is gradully increased, find the value of `mu` for which the cube will topple before sliding.

View SolutionA uniform spherical shell rolls down a fixed inclined pla ne without sliping. Find the ratio of rotational kinetic energy to translational kinetic energy as is reaches lowest point of the incline.
View SolutionA uniform solid sphere is rolled up a fixed rough inclined surface with an initial speed of u. Assuming that there is no slip find the maximum height reached by the sphere over the incline.
View SolutionA body of mass 'm' and radius 'r' rolling on a horizontal floor with velocity 'v', rolls up an inclined plane up to vertical height `(3V^(2))/(4g)`. Find the moment of inertia of body and comment on its shape.
View SolutionA carpet of mass 'm' made of inextensible material is rolled along its length in the form of a cylinder of radius 'R' and is kept on a rough floor. The carpet starts unrolling without sliding on the floor when a very small push is given to it. Calculate the horizontal velocity of the axis of cylindrical part of the carpet when its radius reduces to R/2 .
View SolutionA disc rotating about its axis with angular speed `omega_(0)` is placed lightly (without any translation push) on a perfectly frictionless table. The radius of the disc is R. What are the linear velocities of points A,B and C on the disc shown in Fig. Will the disc roll in the direction indicated ?

View SolutionA solid disc and a ring, both of radius `10cm` are placed on a horizontal table simultaneously, with initial angular speed equal to `10pi rad s^(-1)`. Which of the two will starts to roll earlier ? The co-efficient of kinetic friction is `mu_(k)=0.2`.
View SolutionA cylinder of mass `5kg` and radius `30cm`, free to rotate about its axis, receives an angular impulse of `3kg ms^(-1)` initially followed by a similar impulse after every `4s`.
What is the angular speed of the cylinder `30s` after the initial impulse if the cylinder is at rest initially ?
View Solution
Problems questions and complete solutions for chapter SYSTEM OF PARTICLES AND ROTATIONAL MOTION of JEE (MAIN AND ADVANCED) PHYSICS of Class 11
All Exercises from AAKASH SERIES Class 11 PHYSICS SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- EXERCISE - 1A
- EXERCISE - 1B
- EXERCISE - 2
- EXERCISE - 3
- Exercise-I
- EXERCISE-I (Centre of Mass)
- EXERCISE-I (Rotational Motion :)
- Exercise-II
- EXERCISE-II ( Rolling Motion : )
- EXERCISE-II ( Rotational Dynamics )
- EXERCISE-II (Centre of Mass)
- EXERCISE-II (Conservation of Angular momentum)
- EXERCISE-II (Cross Product)
- EXERCISE-II (Moment of inertia )
- PRACTICE EXERCISE
- PRACTICE EXERCISE (Centre of mass )
- PRACTICE EXERCISE (Conservation of Angular Momentum )
- PRACTICE EXERCISE (Cross Product )
- PRACTICE EXERCISE (Moment of Inertia )
- PRACTICE EXERCISE (Rotational Dynamics )
- Problem
- Problems