Complete Solutions to PRACTICE EXERCISE of chapter SYSTEM OF PARTICLES AND ROTATIONAL MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SYSTEM OF PARTICLES AND ROTATIONAL MOTION |
| AAKASH SERIES | PRACTICE EXERCISE |
| Number Of Questions | 99 |
| Academic Year | 2023-24 |
The centre of mass of two particles with masses 2kg and 6 kg located at (1,1,1), (2,2,1) respectively has the coordinates
View SolutionTwo particles of mass 1 kg and 3 kg have position vectors `2hati + 3hatj+4hatk` and `-2hati+ 3hatj - 4hatk` respectively. The centre of mass, has a position vector
View SolutionIn a molecule of sodium chloride, the masses of sodium and chlorine atoms are in the ratio 23 : 36. If the separation between the two atoms is d., distance of centre of mass of the molecule from sodium atom
View SolutionThe centre of mass of three particles of masses 1 kg, 2 kg and 3 kg is at (2,2, 2). The position of the fourth mass of 4 kg to be placed in the system as that the new centre of mass is at (0, 0, 0) is
View SolutionTwo skaters A and B weighing 40 kg and 60 kg respectively stand facing each other 5 m apart. If they pull a light rope stretched between them, then they meet
View SolutionA uniform bar 8m long has a mass of 6kg. A 10kg mass is tied to one end. The position of centre of mass of the system is
View SolutionTwo persons of masses m and 2m are standing on a horizontal smooth surface of ice. They are initially seperated by a distance d. They are pulling each other holding a rope. They meet at a distance
View SolutionThree particles of masses 1kg, 2kg and 2kg are placed at the corners of an equilateral triangle. The co-ordinates of A,B,C are (0,0) (2,0) and (x,y), the co-ordinates of their centre of mass are
View SolutionMasses each 1 kg are placed at the verticies of an isosceles triangle ABC in which AC = BC = 5cm and AB = 8 cm. The distance of centre of mass of the system from the vertex C is
View SolutionFour particles P,Q,R,S of masses 1kg, 2kg, 3kg and 4kg are placed at the corners of a square of side 1m as shown below. The co-ordinates of the centre of mass of the system are
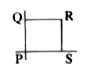
View SolutionTwo uniform rods A and B of same diameter having length 2m and 3m and having mass per unit `4kgm^(-1)` and `6kgm^(-1)` respectively are joined end to end. The position of centre of mass of combined rod from the free end of A
View SolutionTwo discs of radii 2cm and 1cm and made up of same material respectively are placed as shown below. The distance of centre of mass of system from O is
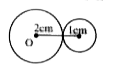
View SolutionTwo particles of masses 2 m and 3 m are at a distance .d. apart. Under their mutual gravitational force, they start moving towards each other. The accelaration of their centre of mass when they are d/2 apart is
View SolutionThree identical particles each of same mass are placed touching each other with their centres on a straight line. Their centres are at A, B and C respectively. Then distance of centre of mass of the system from A is
View SolutionTwo objects of masses 200 g and 500 g possess velocities `10hati ms^(-1)` and `3hati+5hatj ms^(-1)` respectively. The velocity of their centre of mass in `ms^(-1)` is
View SolutionA uniform metre rod is bent at the middle in the form of L shape with the bent arms at `90^(@)` to each other. The distance of the centre of mass from the bent point is
View SolutionParticles of masses 1gm, 2gm, 3gm and 4 gm are placed at x = 1 cm, x = 2cm, x = 3 cm, x = 4 cm respectively. Then `X_(cm)=`
View SolutionFour particles, each of mass 1kg, are placed at the corners of a square of side one meter in the X - Y plane. If the point of intersection of the diagonals of the square is taken as the origin, the coordinates of the centre of mass are
View SolutionThree particles of masses 1 kg, 2 kg, 3 kg are acted upon by forces `(veci +2vecj),(2vecj +3veck) and (veci - veck)` newton respectively. The magnitude of acceleration of centre of mass in m/s^2 is
View SolutionThe mass of a uniform ladder of length 6m is 20kg. A mass 60kg is placed on the ladder at a height of 2m from the bottom. The position of centre of mass from the bottom is
View SolutionA uniform sphere has radius R . A sphere of diameter R is cut from its edge as shown. Then the distance of centre of mass of remaining portion from the centre of mass of the original sphere is

View SolutionA uniform circular disc has a radius of 20cm. A circular disc of radius 10cm is cut concentrically from the original disc. The shift in centre of mass is
View SolutionA man of mass `40kg` in standing on a uniform plank of mass 60kg lying on horizontal frictionless ice. The masn walks from one end to the other end of the plank. The distance walked by the man relative to ice is (given length of plank `=5m`)
View SolutionTwo particles of masses 1kg and 3kg move towards each other under their mutual force of attraction. No other force acts on them. When the relative velocity of approach of the two particles is `2ms^(-1)`, the velocity of centre of mass is `0.5ms^(-1)`. When the velocity of approach becomes `3ms^(-1)` , the velocity of centre of mass is
View SolutionTwo identical particles move towards each other with velocity 2V and V respectively. The velocity of centre of mass is
View SolutionTwo spheres of masses 2M and M are initially at rest at a distance R apart. Due to mutual force of attraction, they approach each other. When they are at separation R/2, the acceleration of the centre of mass of spheres would be
View SolutionA boy of mass 36 kg moves from one end to other end of a boat of mass 72kg on still water. If the length of the boat is `2.7m`, the displacement of the boat is
View SolutionA uniform wire of length `6.28cm` is bent in the form of a circle. The shift in its centre of mass is
View SolutionA block of mass M is placed on the top of a bigger block of mass `10M` as shown in fig. All the surfaces are frictionless. The system is releated from rest. The distance moved by the bigger block by the time the smaller block reaches the ground is
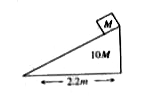
View SolutionThree identical spheres each of radius `3cm` are placed on a horizontal surface touching one another. The distance of centre of mass of system from any centre of the sphere is
View SolutionTwo bodies of masses `4kg` and `2kg` are moving towards each other with `3ms^(-1)` and `2ms^(-1)` respectively. Then velocity of centre of mass is
View SolutionTwo particles of masses 3kg and 2kg move due north and due east respectively with the velocities`2ms^(-1) and 3ms^(-1)`. The magnitude and direction of the velocity of centre of mass is
View SolutionThe distance between the two nucleii of HCl is 1.27A. If the mass of chlorine atom is 37 times that of Hydrogen, the centre of mass of the system from the Hydrogen nucleus is
View SolutionA body of mass 4 kg is attached to another body of mass 2 kg with a massless rod. If the 4 kg mass is at (2i + 5j)m and 2 kg mass is at (4i + 2j)m, the centre of mass of the system is at (in m)
View SolutionTwo spheres of masses 4 kg and 8 kg are moving with velocities `2 ms^(-1) and 3 ms^(-1)` away from each other along the same line. The velocity of centre of mass is
View SolutionA disc of radius R is cut from a larger disc of radius 2R in such a way that the edge of the hole touches of edge of the disc. The centre of mass of the remaining portion is at
View SolutionParticles of masses `1kg` and `3kg` are at `(10i-7j-3k)ms^(-1)` and `(7i-9j+6k)ms^(-1)` then a instantaneous velociti of their centre of masses
View SolutionTwo particles of masses `m_(1)` and `m_(2)` `(m_(1) gt m_(2))` are separated by a distance d. The shift in the centre of mass when the two particles are interchanged.
View SolutionFour identical particles each of mass m are arranged at the corners of a square of sie a. If mass of one of th particle is doubled, the shift in the centre of mass of the system is
View SolutionIf three rods of same mass are placed as shown in the figure, the co-ordinates of the centre of mass of the system are
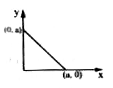
View SolutionSix identicles particles each of mass `0.5kg` are arranged at the corners of a regular hexagon of side length `0.5m`. If one of the particle is removed, the shift in the centre of mass is
View SolutionTwo solids spheres of diameter `d_(1)` and `d_(2)` having material densities `rho_(1)` and `rho_(2)` are placed in contact with each other on the horizontal plane. The height of the combined center of mass from plane
View SolutionA system of two particles is having masses `m_(1)` and `m_(2)`. If the particle of mass `m_(1)` is pushed towards the centre of mass of particles through a distance d, by what distance the particle of mass `m_(2)` should be moved so as to keep the centre of mass of particles at the original position ?
View SolutionThe linear density of a rod of length `L` varies as `rho=A+Bx` where x is the distance from the left end. The distance of centre of mass from O is

View SolutionTwo bodies of masses `m_(1)` and `m_(2)` are moving with velocity `v_(1)` and `v_(2)` respectively in the same direction. The total momentum of the system in the frame of reference attached to the centre of mass I (v is relative velocity between the masses)
View SolutionThe centre of mass coordinates of a block of shape shown in fig. is
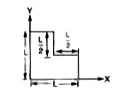
View Solution`(i+i)×(i-j)=`
View SolutionThe radius vector `vecr =2i+5k` and the angular velocity of a particle is w = 3i - 4k. Then the linear velocity of the particle is
View SolutionIf the dot product of two vectors is equal to the magnitude of the cross product of the same vectors, then the angle between the vectors is
View SolutionIf `F = 2i+ 3j - k and r = i- j + 6k` find rx F
View SolutionArea of a parallelogram formed by vectors `(3hati-2hatj+hatk)m` and `(hati+2hatj+3hatk)` m is
View SolutionFind the values of x and y for which vectors `vecA=6hati+xhatj-2hatk and vecB=5hati-6hatj-yhatk` may be parellel
View SolutionIf a,b are the magnitudes of vectors `veca` & `vecb` and `veca.vecb=0` the value of `|vecaxxvecb|` is
View Solution`|AxxB|^(2)+(A.B)^(2)` is equal to
View SolutionIf `vecP=i+j+2k and vecQ=3i-2j+k`, the unit vector perpendicular to both `vecP and vecQ` is
View SolutionTwo sides of a triangle are given by `hati+hatj+hatk and -hati+2hatj+3hatk` then area of triangle is
View SolutionTwo small spheres of mass `5kg` and `15kg ` are joined by a rod of length `0.5m` and of negligible mass. The M.I. of the system about an axis passing through centre of rod and normal to it is
View SolutionMoment of inertia of a hoop suspended from a peg about the peg is
View SolutionThree point masses 3kg, 2kg and 1kg are placed at A,B,C of a triangle. AB = 0.3,m AC = 0.5 m and BC = 0.4 m. The M.I of the system about an axis through A and normal to the plane of triangle is
View SolutionThe M.I of a uniform thin circular ring about an axis through its centre and normal to the plane of ring is I. Its M.I about a tangent in its plane is equal to
View SolutionRatio of densities of materials of two circular discs of same mass and thickness is `5:6`. The ratio of their M.I about natural axes is
View SolutionMoment of inertial of a uniform horizontal solid cylinder of mass M about an axis passing through its edge and perpendicular to the axis of the cylinder when its length is 6 times its radius R is
View SolutionM.I of a solid sphere about its diameter is `64kgm^(2)`. If that sphere is recast into 8 identical small spheres, then M.I of such small sphere about its diameter is
View SolutionTwo thin uniform circular rings each of radius `10m` and mass `0.1kg` are arranged such that they have common centre and their planes are prependicular to each other. The M.I. of the system about an axis passing through their common centre and perpendicular to the plane of either of the rings in kg `m^(-2)` is
View SolutionThe radius of gyration of a hollow sphere about a tangent is
View SolutionConsider a uniform square plate of side 'a' and mass 'm'. The moment of inertia of this plate about an axis perpendicular to its plane and passing through one of its corner is
View SolutionThe M.I. of a thin circular disc about a tangent in the same plane of disc is I. Then M.I. about one of the diameters is
View SolutionThree uniform discs each of mass 'm' and radius 'r' are kept touching each other, such that their centres form a triangle. The M.I. of the system about a median of
View SolutionA thin circular ring of mass 'm' and radius R is rotating about its axis with a constant angular velocity `omega`. Tho objects each of mass M are attached gently to he opposite ends of a diameter of the ring. The new angular velocity of ring is
View SolutionThe M.I. of a uniform disc about an axis passing through its centre and perpendicular to its plane is `1kgm^(2)`. It is rotating with an angular velocity to `100rads^(-1)`. A second disc of same mass and radius is joined to it coaxially. Now these two discs together continue to rotate about the same axis. Then the lose in kinetic energy in kilo joules is
View SolutionA particle of mass 2kg is moving such that at time t its position in meter is given by `barr(t)=5hati-2t^(2)hatj`. The angular momentum of the particle at `t=2s` about the origin in `kgm^(-2)s^(-1)` is
View SolutionA ring of mass M and radius R is rotating about its axis with angular velocity `omega`. Two identical bodies each o mass m are now gently attached at the two ends of a diameter of the ring. Because of this, the kinetic energy loss will be
View SolutionCircular disc of mass 2kg and radius 1 metre is rotating about an axis perpendicular to its plane and passing through its centre of mass with a rotational kinetic energy of 8Joules. The angular momentum in (J sec) is
View SolutionA persons is spinning with his hands outstretched at th rate of `4` rad `s^(-1)`. When he brings his hands close to the body, he spins at the rate of `16` rad `s^(-1)`. The ratio of M.I. in the two cases susccessively is
View SolutionA dancer spins about a vertical axis at `60` rpm with her arms folded. If she strectes her hands so that M.I. about the vertical axis increases by `25%` the new rate of revolvution is
View SolutionTwo identical disc are placed one over the other and both are rotating about a common axis through their centre and normal to their frame with angular velocity `omega`. If the upper disc is suddenly removed, angular velocity of the other disc would be
View Solution`barF=abari+3barj+6bark` and `barr=2bari-6barj-12bark`. The value of 'a' for which the angular momentum is conserved is
View SolutionIf earth shrinks to `1//64` of its volume with mass remaining same duration of day will be
View SolutionTwo wheels of M.I. `3kgm^(2)` and `5kgm^(2)` are rotating at a rate of `600` rpm and `800` rpm respectively in opposite directions. If they are coupled so as to rotated with the same axis of rotation , the resultant speed of rotation (in rpm)
View SolutionA mass is whirled in a circular path with a constant angular velocity and its angular momentum is L. If the length of string is now halved keeping the angular velocity same, the new angular momentum is
View SolutionA square plate of moment of inertia 'I' is pivoted at its centre. It has a small projection of neglegible mass to one of its sides. A particle of mass 'm' moving with a velocity v parallel to the side having projection strikes to projection and stricks to it. If 'l' is the side length, the angular velocity of plate is
View SolutionA flywheel of M.I. `6xx10^(-2)kgm^(2)` is rotating with an angular velocity of `20rads^(-1)` . The torque required to bring it to rest in `4s` is
View SolutionWhen `200J` of work is done on a fly wheel its frequency of rotation increases from `4Hz` to `9Hz`. The M.I. of the wheel about the axis of rotation is
View SolutionThe shaft of a motar is making `1260 RPM`. The torque supplied by the motor is `100Nm`. The power of motor is
View SolutionA solid sphere is rotating with an angular velocity `omega`. It is of moment is inertia 'I' about its diametrical axis and is of linear expansion coefficient `alpha`. When temperature is increased by `DeltaT`, the fractional change in its angular velocity is
View SolutionThe moment of inertia of a wheel of radius `20cm` is `40kgm^(2)`. If a tangential force of `80N` applied on the wheel , its Rotational K.E. after `4s` is
View SolutionA thin rod of mass 'm' and length 2L is made to rotate about a normal axis through centre of rod. If its angular velocity changes from 'O' to `'omega'` in time 't'. The torque acting on it is
View SolutionThe M.I. of a body is `1.2kgm^(2)`. Initially the body is at rest. In order to produce a rotational kinetic energy of `1500J` an angular acceleration of `25rads^(-2)` must be applied about the axis for a duration of
View SolutionA uniform solid sphere of diameter `0.2m` and mass `10kg` is rotated about its diameter with an angular velocity of `2rads^(-1)`. Then its angular momentum is `kgm^(2)s^(-1)` is
View SolutionIf the K.E. of a rotating body about an axis is decreased by `36%`, its angular momentum about that axis
View SolutionA constant torque acting on a uniform circular wheel changes its angular momentum from A to 4 A in 4S. The torque acted on it is
View SolutionA solid sphere and a hallow sphere of same mass and radius rotate about their diameter with same K.E. If torques of equal magnitude are applied on them, the ratio of their angular displacement before they are brought to rest is
View SolutionFor the arrangement shown in the figure, tension in the string is
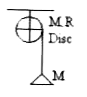
View SolutionA ring is allowed to roll down on an incline of `1` in `10` without slipping. The acceleration of its centre of mass is
View SolutionA cylinder is released from rest from the top of an incline of inclination `theta` and length 'l' . If the cylinder roles without slippling its speed at the bottom
View SolutionFor a body rolling along a level surface, without slipping the translational and rotational kinetic energies are in the ratio `2:1`. The body is
View SolutionA solid sphere and a spherical shell roll down an incline from rest from same height. The ratio of times taken by them is
View SolutionWhen a solid sphere is rolling along level surface the percentage of its total kinetic energy that is translational is
View SolutionA solid sphere of radius 'r' is rolling on a horizontal surface. The ratio between the rotational kinetic energy and total energy
View Solution
PRACTICE EXERCISE questions and complete solutions for chapter SYSTEM OF PARTICLES AND ROTATIONAL MOTION of JEE (MAIN AND ADVANCED) PHYSICS of Class 11
All Exercises from AAKASH SERIES Class 11 PHYSICS SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- EXERCISE - 1A
- EXERCISE - 1B
- EXERCISE - 2
- EXERCISE - 3
- Exercise-I
- EXERCISE-I (Centre of Mass)
- EXERCISE-I (Rotational Motion :)
- Exercise-II
- EXERCISE-II ( Rolling Motion : )
- EXERCISE-II ( Rotational Dynamics )
- EXERCISE-II (Centre of Mass)
- EXERCISE-II (Conservation of Angular momentum)
- EXERCISE-II (Cross Product)
- EXERCISE-II (Moment of inertia )
- PRACTICE EXERCISE
- PRACTICE EXERCISE (Centre of mass )
- PRACTICE EXERCISE (Conservation of Angular Momentum )
- PRACTICE EXERCISE (Cross Product )
- PRACTICE EXERCISE (Moment of Inertia )
- PRACTICE EXERCISE (Rotational Dynamics )
- Problem
- Problems