Complete Solutions to Exercise-II of chapter SYSTEM OF PARTICLES AND ROTATIONAL MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SYSTEM OF PARTICLES AND ROTATIONAL MOTION |
| AAKASH SERIES | Exercise-II |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Centre of mass of two particle with masses 2 kg and 1 kg locsted at (1, 0, 1) and (2, 2, 0) has the co - ordinates of
View SolutionParticles of masses 100 and 300 gram have position vectors `(2hat(i)+5hat(j)+13hat(k))` and `(-6hat(i)+4hat(j)+2hat(k))`. Position vector of their centre of mass is
View SolutionThe distance between the centres of carbon and oxygen atoms in the carbon monoxide gas molecule is `1.13xx10^(-10)m`. The distance of centre of mass of the molecule relative to carbon atom is
View SolutionThe co - ordinates of centre of mass of particle of mass 10, 20 and 30 gm are (1, 1, 1) cm. The position co - ordinates of mass 40 gm which when added to the system, the position of combined centre of mass be at (0, 0, 0) are,
View SolutionTwo particles of masses 4 kg and 6 kg are at rest separated by 20 m. If they move towards each other under mutual force of attraction, the position of the point where they meet is
View SolutionA ball of mass 3M rolls from rest on a smooth flat table towards another ball of mass 2M at rest with a constant velocity `5m//s`. When the two balls are separated by a distance `6m`, the position of centre of mass from the mass `3M` is
View SolutionOne end of a thin uniform rod of length L and mass `M_(1)` is rivetted to the centre of a uniform circular disc of radius 'r' and mass `M_(2)` so that that both are coplanar. The centre of mass of the combination from the centre of the disc is (Assume that the point of attachment is at the origin).
View SolutionThree particles of masses 1 kg, 2 kg and 3 kg are placed at the vertices A, B and C of an equiliateral triangle ABC. If A and B lie at (0, 0) and (1, 0) m, the co - ordinates of their centre of mass are
View SolutionThree particle each of 1kg mass are placed at corners of a right angled triangle AOB, .O. being the origin of coordinate system (OA and OB along the x - direction and + ve y-direction). If OA = OB = 1m, the position vector of centre of mass (in metres) is
View SolutionFour particles of masses 2,2,4,4 kg are arranged at the corners A,B,C,D of a square ABCD of side 2m as shown in the figure. The perpendicular distance of their centre of mass from the side AB is

View SolutionTwo uniform rods A and B of lengths 5 m and 3m are placed end to end. If their linear densities are 3 kg/m and 2 kg/m, the position of their centre of mass from their interface is
View SolutionA uniform disc of radius R is put over another uniform disc of radius 2R of same thickness and density. The peripheres of the two discs touch eachother. The position of their centre of mass is
View SolutionA system consists of two identical particles one particle is at rest and the other particle has an acceleration .a.. The centre of mass if the system has an acceleration of
View SolutionThree identical spheres each of radius .R. are placed touching each other so that their centres A, B and C lie on a straight line. The position of their centre of mass from A is
View SolutionThe velocities of three particles of masses 20 g, 30 g and 50 g are `10hat`i, `10hatj` and `10hatk` respectively. The velocity of the centre of mass of the three particles is
View SolutionA thin uniform rod of length L is bent at its mid point as shown in the figure. The distance of centre of mass form the point .O. is

View SolutionParticles of masses m, 2m, 3m ... nm gram are placed on the same line at distance l, 2l, 3l, ..., nl cm from a fixed point. The distance of centre of mass of the particles from the fixed point in cm is
View SolutionFour particles, each of mass 1kg, are placed at the corneres of a square OABC of side 1m. .O. is at the origin of the coordinate system. OA and OC are aligned along positive x-axis and positive y-axis respectively. The position vector of the centre of mass is (in .m.)
View SolutionThree identical masses are kept at the corners of an equilateral triangle ABC. A moves towards B with a velocity V,B moves towards C with velocity V and C moves towards A with same velocity V. Then the velocity of centre of mass of the system of particles is
View SolutionThree particles of masses 8 kg, 4 kg and 4 kg situated at (4,1), (-2,2) and (1,-3) are acted upon by external forces `6bar(j)N,-6 bar(i)N` and `14 bar(i)N`. The acceleration of centre of mass of the system is
View SolutionThe mass of a uniform ladder of length 6m is 20kg. A mass 60kg is placed on the ladder at a height of 2m from the bottom. The position of centre of mass from the bottom is
View SolutionFrom a sphere of radius 1m, a sphere of radius `0.5m` is removed from the edge. The shift in the C.M. is
View SolutionA circular plate has a uniform thickness and has a diameter 56cm. A circular disc of diameter `42cm` is removed from one edge of the plate. The distance of centre of mass of the remaining portion from the centre of the circular plate is
View SolutionA man of 50kg is standing at one end on a boat of length 25m and mass 200kg. If he starts running and when he reaches the other end, h has a velocity `2ms^(-1)` with respect to the boat. The final velocity of the boat is (in `ms^(-1)`)
View SolutionTwo particles having masses m and 2m are travelling along x-axis on a smooth surface with velocities `u_(1)` and `u_(2)`, collide. If their velocities after collision are `v_(1)` and `v_(2)`, then the ratio of velocities of their centre of mass before ans impact is
View SolutionTwo particles A and B initially at rest, move towards each other, under mutual force of attraction. At an instance when the speed of A is v and speed of B is 2v, the speed of centre of mass (CM) is
View SolutionA baloon of mass M is stationary in air. It has a ladder on which a man of mass m is standing. If the man starts climbing up the ladder with a velocity v relative to ladder, the velocity of balloon is
View SolutionA woodrn log of mass 120 kg is floating on still water perpendicular to the shore. A man of mass 80 kg is standing at the centre of mass of the log and he is at a distance of 30 m from the shore. When he walks through a distance of 10 m towards the shore and halts, now his distance from the shore is
View SolutionA uniform wire of length L is bent in the form of a circle. The shift in its centre of mass is
View SolutionMasses 1 kg, 1.5 kg, 2 kg and M kg are situated at (2, 1, 1) (1, 2, 1) (2, -2, 1) and (-1, 4, 3). If the their centre of mass is situated at (1, 1, 3/2), the value of M is
View SolutionThree identical spheres each of radius R are placed on a horizontal surface touching one another. If one of the spheres is removed, the shift in the centre of mass of the system is
View SolutionTwo bodies of mases 5kg and 3kg are moving towards each other with `2ms^(-1)` and `4ms^(-1)` respectively. Then velocity of centre of mass is
View SolutionTwo particles each of the same mass move due north and due east respectively with the same velocity .V.. The magnitude and direction of the velocity of centre of mass is
View SolutionIf the distance between the centres of the atoms of potassium and bromine in KBr (potassium - bromide) molecule is `0.282xx10^(-9)`m, find the centre of mass of this particle system from potassium (mass of bromine = 80 u, and of potassium = 39 u).
View SolutionThe co-ordinates of the centre of mass of the system as shown in figure are
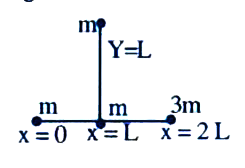
View SolutionTwo bodies of masses 10 kg and 20 kg are located in x-y plane at (0, 1) and (1, 0). The position of their centre of mass is
View SolutionA uniform disc of diameter R/2 is put over another uniform disc of diameter R of same thickness and density. The peripheries of the two disc touch each other. The centre of mass of the system from centre of big disc is
View SolutionParticles of masses 1 kg and 3 kg at `(2i+5j+13 k)` m and `(-6i+4j-2k)m` then instantaneous position of their centre of mass is
View SolutionTwo particles of same mass are projected simultaneously with same speed `20ms^(-1)` from the top of a tower of height `20m`. One is projected vertically upwards and other projected horizontally. The maximum height attained by centre of mass from the ground will be `(g=10ms^(-2))`
View SolutionSix identical particles each of mass m are arranged at the corners of a regular hexagone of side length s. If the mass of one of the particle is doubled, the shift in the centre of mass is
View SolutionThree identical rods each of length L and mass m are joined to form a U -shape as shown in figure. The distance of centre of mass of combined system from the corner .O. is
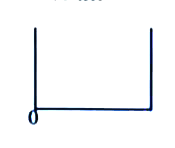
View SolutionFour identical particles each of mass 1 kg are arranged at the corners of a square of side length `2sqrt(2)`m. If one of the particles is removed, the shift in the centre of mass is
View SolutionThe cross product of the vectors `(2i - 3j + 4k) and (I + 4j -5k)` is
View SolutionA particle of mass 0.2 kg is moving with linear velocity `(i-j+2k)`. If the radius vector `r=4i+j-k`, the angular momentum of the particle is
View SolutionThe scalar and vector products of two vectors are `48sqrt(3)` and 144 respectively. What is angle between the two vectors?
View SolutionA force of `- F hat(k)` acts on O, the origin of the coordinate system. The torque about the point (1, -1) is
View SolutionThe adjacent sides of a parallelogram are `vec(P)=2i-3j+k` and `vec(Q)=-2i+4j-k`. What is the area of the parallelogram ?
View SolutionWhat is the condition for the vectors `2i + 3j - 4k and 3i - aj + bk` to be parallel ?
View Solutiona,b are the magnitudes of vectors `veca` & `vecb` . If `vecaxxvecb=0` the value of `veca.vecb` is
View SolutionIf `|vec(A)| = 4N, |vec(B)| = 3N` the value of `|vec(A) xx vec(B)|^(2) + |vec(A).vec(B)|^(2) =`
View SolutionIf `vecA=2hati+3hatj+6hatk` and `vecB=3hati-6hatj+2hatk` then vector perpendicular to both `vecA` and `vecB` has magnitude K times that of `6hati+2hatj-3hatk`. Then `K=`
View SolutionVertices of a triangle are given by `hati+3hatj+2hatk` , `2hati-hatj+hatk` and `-hati+2hatj+3hatk` then area of triangle is (in units)
View SolutionThree identical spherical shells, each of mass m and radius r are placed as shown in figure. Consider an axis XX. which is thouching to two shells and passing through diameter of third shell. Moment of inertia of the system consisting of these there spherical shells about XX. axis is

View SolutionTwo small spheres of masses 10 kg and 30 kg are joined by a rod of length 0.5 m and of negligible mass. The M.I of the system about a normal axis through centre of mass of the system is
View SolutionA ring has a mass of 0.5 kg and radius 1 m. The moment of inertia of the ring about its diameter is
View SolutionFour particles each of mass 1 kg are at the four corners of a square of side 1m. The M.I of the system about a normal axis through centre of square is
View SolutionThe radius of gyration of a body about an axis at a distance of 4cm from its centre of mass is `5cm`. The radius of gyration about a parallel axis through centre of mass is
View SolutionTwo discs have the same mass and thickness. Their materials are of densities `d_(1)` and `d_(2)`. The ratio of their M.I about their central axis is
View SolutionThe moment of inertia of a cylinder about its own axis is equal to its mo0ment of inertia about an axis passing throughj its centre and normal to its length. The ratio of length to radius is
View SolutionTwo circular loops of radii R and nR are made of same wire. If their M.I about their normal axis through centre are in the ratio 1 : 8, the value of n is
View SolutionThree identical rings, each of mass M and radius R are placed in the same plane touching each other such that their centers from the vertices of an equilateral triangle. The M.I of the system about an axis passing through center of one of the rings and perpendicular to its plane is
View SolutionThe radius of gyration of a solid sphere of radius .R. about its tangential axis is
View SolutionA straight thin uniform rod of length 4L and man 4M is bent into a square. Its M.I about one side is
View SolutionThe moment of inertial of an uniform circular disc about its central axis I 'I' . Its M.I about a tangent in its plane is equal to
View SolutionTwo circular rings of equal mass and radius are placed touching each other. The moment of inertia of the system about tangential axis in the plane of system passing through point of contact of rings is
View SolutionMoment of inertia of a thin square plate about an axis passing through its diagonal is I. Its moment of inertia about an axis passing through its centre in the plane of the plate and making an angle `theta` with the diagonal is
View SolutionTwo identical rods are joined to form an 'X'. The smaller angle between the rods is `theta`. The moment of inertia of the system about and axis passing through the point of intersection of the rods and perpendicular to their plane is
View SolutionA thin wire of length l having linear density `rho` is bent into a circular loop with C as its centrem as shown in figure. The moment of inertia of the loop about the line AB is

View SolutionIf the mass of earth and radius suddenly become 2 times and 1/4 th of the present values the length of the day becomes
View SolutionA child is standing with folded hands at the centre of a platform rotating about its central axis. The K.E of the system is K. The child now stretches his arms so that the M.I of the system doubles. The K.E of the system now is
View SolutionA ballet dancer spins about a vertical axis at 60 rpm with his arms closed. Now he stretches his arms such that M.I increases by 50%. The new speed of revolution is
View SolutionA circular disc is rotation about its natural axis with angular velocity of `10rads^(-1)`. A second disc of same mass is joined to it coaxially. If the radius of disc is half of the radius of the first, then they together rotate with an angular velocity of
View SolutionA shell of mass of mass 'm' is projected with a velocity 'v' at an angle `60^(@)` to horizontal. When it reaches the maximum height, its angular momentum with respect to point of projection is
View SolutionDensity remaining constant, if earth contracts to half of its present radius, duration of the day would be (in minutes).
View SolutionTwo wheels of M.I. `3kgm^(2)` and `5kgm^(2)` are rotating at a rate of `600` rpm and `800` rpm respectively in opposite directions. If they are coupled so as to rotated with the same axis of rotation , the resultant speed of rotation (in rpm)
View SolutionA mass is whirled in a circular path with an angular momentum L. If the length of string and angular velocity, both are doubled, the new angular momentum is
View SolutionIf a disc of mass m and radius R totates with an angular acceleration a, of the torque acting on the disc is
View SolutionA merry-go-round, made of a ring-like platform of radius R and mass M is revolving with angular speed `omega`. A person of mass M is standing on it. At one instant, the person jumps off the round, radially away from the centre of the round (as seen from the round). The speed of the round afterwards is
View SolutionThe diameter of a rotating fly wheel is R. Its coefficient of linear expansion is `alpha`. If the temperature is increased by `DeltaT`, the percentage change in its rotational KE would be
View SolutionKeeping the mass of earth as constant, if its radius is reduced to `1//4^(th)` of its initial value, then the period of revolution of earth about its own axis and passing through the centre, in hours, is. Assume earth to be a solid sphere and its initial period of rotation as 24 hrs.
View SolutionA uniform circular disc of radius 50cm at rest is free to turn about an axis which is perpendicular to its plane and passes through its centre. It is subjected to a torque which produces a constant angular acceleration of `2.0rads^(-2)`. Its net acceleration in `ms^(-2)` at the end of `2.0` s is approximately
View SolutionThe handle of a door is at a distance 40 cm from axis of rotation. If a force 5Nis applied on the handle in a direction `30^(@)` with plane of door, then the torque is
View SolutionA particle of mass m is projected with an initial velocity u at an angle `theta` to horizontal. The torque of gravity on projectile at maximum height about the point of projection is
View SolutionA constant torque of 1000 N-m, turns á wheel of moment of inertia 200 `kg-m^(2)`about an axis through its centre. Its angular velocity after 3 s is, (in rad/s)
View SolutionIf `484J` of energy is spent in increasing the speed of wheel from 60 rpm to 360 rpm, the M.I of the wheel is
View SolutionA shaft rotating at 3000 rpm is transmitting a power of 3.14 KW. The magnitude of the driving torque is
View SolutionA wheel rotating at angular speed of `20rads^(-1)`, is brought to rest by a constant torque in 4s. If the M.I is `0.2kgm^(2)`, the work done in first `2s` is
View SolutionA thin uniform rod of length l and mass m is swinging freely about a horizontal axis passing through its end. Its maximum angular speed is `omega`. Its centre of mass rises to a maximum height of
View SolutionThe K.E. of a body rotating at 300 rpm is 62.8 J. Its angular momentum is
View SolutionIf the velocity of a rotating body of mass 50 kg is given by `bar(V)=3bar(i)+4bar(j)+5bar(k)` and radius vector `bar(r )=2bar(i)+3bar(j)+4bar(k)`, then its angular momentum is.
View SolutionIf the Earth shirnks such that its density becomes 8 times to the present value, then the new during of the day in hours will be
View SolutionA point sized sphere of mass .m. is suspended from a point using a string of length .l.. It is then pulled to a side till the string is horizontal and released. As the mass passes through the portion where the string is vertical, magnitude of its angular momentum is
View SolutionTwo rigid bodies have same angular momentum about their axes of symmetry. If same torque is applied about their axes, the ratio of times after which they will be stopped is
View SolutionOne end of a uniform rod of mass m and length l is clamped. The rod lies on a smooth horizontal surface and rotates on it about the clamped end at a uniform angular velocity `omega`. The force exerted by the clamp on the rod has a horizontal component.
View SolutionA cubical block of mass M and edge a slides down a rough inclined plane of inclination `theta` with a uniform velocity. The torque of the normal force on the block about its centre has a magnitude
View SolutionA particle of mass m is moving yz-plane with a uniform velocity v with its trajectory running parallel to `+ve` y-axis and intersecting z-axis at z=a. The change in its angular momentum about the origin as it bounces elastically from a wall at y= constant is
View SolutionA mass m is supported by a massless string wound around a uniform hollow cylinder of mass m and radius R. If the string does not slip on the cylinder, with what acceleration will the mass falls on release ?
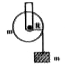
View SolutionA wheel which is initially at rest is subjected to a constant angular acceleration about its axis. It rotates through an angle of `15^@` in time t sec. The increase in angle through which it rotates in the next 2t sec is
View SolutionA car is negotiating a curved road of radius R. The road is banked at an angle `theta`. The coefficient of friction between the types of the car and the road is `mu_(s)`. The maximum safe velocity on this road is
View SolutionA solid cylinder of mass `50kg` and radius `0.5m` is free to rotate about the horizontal axis. A massless string is wound round the cylinder with one end attached to it and other hanging freely. Tension in the string required to produce an angular acceleration of 2 revolutions `s^(-2)` is
View Solution
Exercise-II questions and complete solutions for chapter SYSTEM OF PARTICLES AND ROTATIONAL MOTION of JEE (MAIN AND ADVANCED) PHYSICS of Class 11
All Exercises from AAKASH SERIES Class 11 PHYSICS SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- EXERCISE - 1A
- EXERCISE - 1B
- EXERCISE - 2
- EXERCISE - 3
- Exercise-I
- EXERCISE-I (Centre of Mass)
- EXERCISE-I (Rotational Motion :)
- Exercise-II
- EXERCISE-II ( Rolling Motion : )
- EXERCISE-II ( Rotational Dynamics )
- EXERCISE-II (Centre of Mass)
- EXERCISE-II (Conservation of Angular momentum)
- EXERCISE-II (Cross Product)
- EXERCISE-II (Moment of inertia )
- PRACTICE EXERCISE
- PRACTICE EXERCISE (Centre of mass )
- PRACTICE EXERCISE (Conservation of Angular Momentum )
- PRACTICE EXERCISE (Cross Product )
- PRACTICE EXERCISE (Moment of Inertia )
- PRACTICE EXERCISE (Rotational Dynamics )
- Problem
- Problems